融入兴趣区域的差分隐私轨迹数据保护方法*

兰 微，林 英,+，包聆言，李 彤，陈梦蓉，单今朝

1.云南大学 软件学院，昆明650091

2.云南省软件工程重点实验室，昆明650091

1 引言

基于位置的服务[1]（location-based services，LBS）是通过利用路径与地理位置信息为人们提供服务的一个新兴领域，能为人们提供距离最近的商场、影院、ATM 机，日常出行中的导航信息，以及交通拥堵信息等。但用户使用LBS，必须提供自己的位置相关信息。通过对一个或多个移动对象位置相关信息的采样所获得的数据信息根据采样先后顺序就构成了轨迹数据。

轨迹数据中包含了位置、时间、速度等与用户隐私直接相关的信息，若不对原始轨迹数据进行保护而直接发布，轨迹数据的关联性与时空特征使得攻击者很容易地推断出用户的行为模式与习惯，同时攻击者还可以根据用户的历史移动轨迹数据特征，挖掘出其活动范围和活动场景[2]。根据文献[3]的报道，在150 万条匿名移动轨迹数据中，若无外部背景知识，随机给出两个时空数据点，50%以上的个人敏感移动轨迹可以被鉴别出来，随机给出4 个时空点，便可以鉴别出95%的个人敏感移动轨迹。再者，随着近年来大数据和物联网相关技术的快速发展，极大地促进了轨迹数据挖掘技术[4-6]的发展，也导致用户轨迹数据中的隐私信息更易于受到攻击。因此，如何控制轨迹数据的发布和访问是一个重要的研究问题。为实现轨迹数据发布隐私保护，研究者们提出了各种保护用户轨迹隐私的手段，如You等[7]、Gao等[8]基于随机方法和旋转方法，生成一定数量的假轨迹，达到迷惑攻击者的目的。Chen 等人[9]提出（K，C）L隐私模型，对敏感位置数据使用局部抑制的方法来实现轨迹数据的匿名。Abul 等人[10]提出（k-δ）匿名模型，使得发布的匿名集中的轨迹数量大于等于匿名数值k，且匿名集中任何两条轨迹的距离（欧式距离）小于等于不确定性阈值δ。

传统轨迹数据发布方法主要可以分为假数据[11]、抑制[12]及泛化[13]三种。假数据法是通过生成一些假轨迹对原始轨迹数据进行干扰，并且保证被干扰的轨迹数据的某些统计属性不发生严重失真。抑制法主要通过不发布轨迹上的某些敏感位置或频繁访问的位置以实现隐私保护。泛化法将轨迹上所有的采样点都泛化为对应的匿名区域，以达到隐私保护的目的。

假数据、抑制及泛化三种方法各有优缺点及不同的适用场景，其中假轨迹隐私保护方法简单，计算量小，但容易造成假数据的存储量大及数据可用性降低等缺点。因此，该方法适用于实时性较高并且对数据可用性要求不高的系统。抑制法能保证用户较高的隐私保护度，然而过多的轨迹片段被抑制会造成巨大的信息损失。因此，该方法适用于隐私保护度高并且对数据可用性要求不高的系统。泛化法主要基于轨迹相似性进行轨迹聚类，但不合适的轨迹相似性度量会导致匿名过程中不必要的信息损失，从而降低轨迹数据的可用性。

以上三种隐私保护模型均无法提供一种有效且严格的方法来证明其隐私保护水平，因此2008 年Dwork[14]提出了一种更为严格的可证明隐私定义，即差分隐私保护方法。作为一种新的隐私保护模型，差分隐私保护无需考虑攻击者所拥有的任何可能的背景知识，因此自诞生以来迅速被业界认可，并成为了隐私保护领域的研究热点。

差分隐私保护最初被应用于统计数据库安全领域，旨在发布统计信息时保护数据库中个体的隐私信息。2012 年，Chen 等[15]首次提出将差分隐私用于对轨迹数据的保护，通过对轨迹数据加入Laplace 噪声保证挖掘结果满足差分隐私需求，从而实现对运输信息的轨迹隐私保护。差分隐私机制自此也被用来进行轨迹隐私保护。

目前，针对轨迹数据的差分隐私保护还是一个新兴研究领域，存在两个主要问题亟待解决：

（1）如何在保护用户隐私的前提下减少噪声数据带来的误差，从而提高数据的可用性。在进行轨迹数据的隐私保护时，对全部数据集进行直接保护，会极大降低数据的可用性。因此，如何通过适当的方法在所有轨迹数据中选择部分数据进行隐私保护为一大难点。例如，某一用户一天的轨迹中存在560个位置点，如果直接对每个轨迹点进行保护，将造成严重信息损失，导致保护后发布的轨迹可用性极低。

（2）如何保证算法在满足差分隐私的前提下，尽量提高数据的隐私保护程度。

为解决上述问题，本文提出了一种融入频繁兴趣区域进行差分隐私保护的轨迹数据保护方法。本文的主要工作如下：

（1）将轨迹数据中位置点集中出现的区域定义为兴趣区域，以驻留点的形式代表兴趣区域内所有位置点，在基本保持原有轨迹时序关系的前提下，精简了轨迹中大量物理位置相近的数据点。

（2）通过对驻留点进行频繁模式挖掘，发现用户的频繁驻留点，然后基于Laplace 机制，对频繁驻留点进行加噪。传统方法对所有轨迹数据点均进行加噪，而本文方法只需对部分轨迹数据点进行加噪，在保护用户隐私的前提下，极大提高了数据的可用性。

（3）分别在公开的真实轨迹数据集和仿真轨迹数据上设计了详细的实验，以验证本文方法的有效性。与三种现有方法进行了详细对比，并详尽地报告了实验过程和结果。

2 差分隐私

发布数据信息时，信息发布者需要对数据信息中的个体隐私信息进行保护，差分隐私保护模型由此产生。差分隐私保护模型可实现在数据集中插入或删除某一条记录后，不会对输出结果产生显著影响的数据保护效果。

差分隐私保护下的数据发布，根据实现环境不同可以分为交互式数据发布和非交互式数据发布[7]，因此差分隐私保护下的轨迹数据保护也主要分为这两种方式。在交互式环境下，用户向轨迹数据管理者提出查询请求，轨迹数据管理者根据用户查询请求对轨迹数据集进行操作，并将结果进行模糊化后反馈给用户；在非交互式环境下，轨迹数据管理者针对可能的查询，在满足差分隐私的条件下一次性发布所有模糊化后的结果。本文主要考虑的为非交互环境下的轨迹数据发布。

2.1 相关定义

定义1（ε-差分隐私）设有随机算法M，对于任意两个相邻数据集D和D′，若算法M在D和D′上的任意输出结果S满足：

则称算法M提供ε-差分隐私保护，其中参数ε称为差分隐私预算。ε控制隐私保护水平，ε越大，添加的噪声越小，则隐私保护水平越低。ε越小，添加的噪声越大，则隐私保护水平越高。当ε等于0 时，达到最高保护水平，此时经过加噪后的数据已无法反映与原数据相关的任何有效信息。

定义2（全局敏感度[16]）设有函数f:D→Rd，输入为一数据集D，输出为一个d维实数向量。对于任意的相邻数据集D和D′，函数f的全局敏感度为：

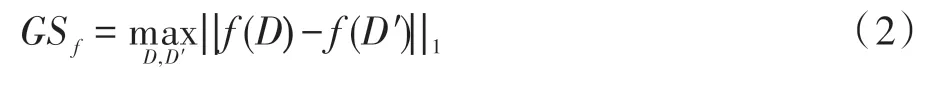
其中，R表示所映射的实数空间，d表示函数f的查询维度，||f(D)-f(D′)||1是f(D)和f(D′)之间的L1距离。敏感度是控制删除数据集中某一记录后对查询结果造成的最大影响，函数的全局敏感度与数据集无关，仅与函数本身有关，且不同函数有不同的全局敏感度，其中噪声大小与全局敏感度紧密相关。

2.2 实现机制

噪声机制是实现差分隐私的主要技术，常用的噪声机制有两种：Laplace机制[16]和指数机制[17]。

Laplace 机制适用于数值型数据，其思路为根据Laplace 分布生成随机噪声，并将产生的随机噪声加入原始数据，以实现ε-差分隐私保护，Laplace 分布的概率密度函数为：

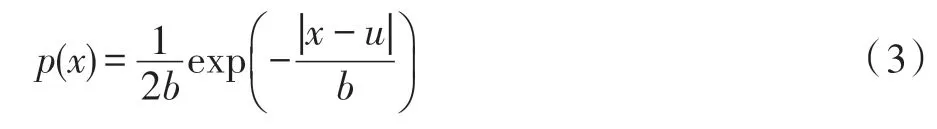
称随机变量x服从参数为b和u的Laplace分布。

定义3（Laplace 机制[16]）给定数据集D，设f:D →Rd是一个敏感度为Δf的函数。

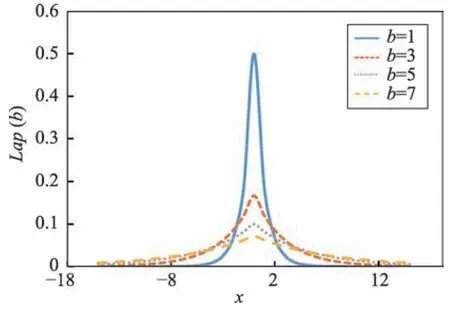
Fig.1 Probability density function of Laplace图1 Laplace概率密度函数

为生成服从Laplace 分布的噪声，主要利用构造逆函数的方法：

其中，U是服从均匀分布（0,1）的随机数，F-1为F的逆函数。当有多个x满足逆函数时，只取值最小的x。

Laplace分布函数如下：

由上述分布函数即可生成服从Laplace 分布的随机数X。

与只适用于数值型数据的Laplace 机制相比，指数机制适用于非数值型数据的查询和处理。

定义4（指数机制[17]）设有可用函数u:(Dn×R)→R，输出为一实体对象r∈Range，若算法A满足下列等式，则A满足ε-差分隐私。

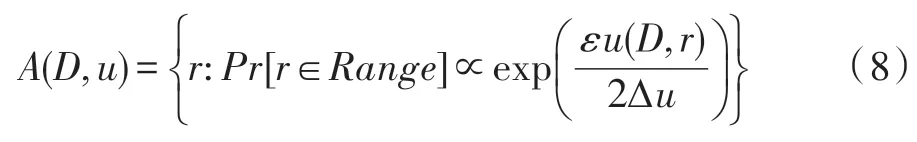
其中，Δu为可用函数的全局敏感性，算法A以正比于的概率返回实体对象。由式（8）可知，打分越高，被选择输出的概率越大。

由于本文研究的是本质为实数序列的轨迹数据，因此选择Laplace机制实现加噪。

3 相关工作

将差分隐私应用到保护轨迹数据发布，最早见于Chen 等人[15]将Laplace 噪声添加到轨迹序列模式对应的真实支持度计数，并在此基础上构建前缀序列树，最终发布满足差分隐私的轨迹数据库。后续为降低序列维度的影响，提高挖掘结果的可用性，Chen等人[18]提出了n-gram 算法限制序列的最大长度。文献[19]认为轨迹中的每一个位置都有可能暴露用户隐私，因此提出一种结合速度与轨迹角度的生成噪声的方法对所有位置点进行保护。Shao 等人[20]提出了一种结合采样和插值的算法，打破了传统差分隐私先验敏感度的框架。Alaggan 等人[21]认为传统差分隐私在无形中为用户决定了隐私保护程度，这样使得隐私保护方法缺乏灵活性。为解决这一问题，他们提出一种显示机制来实现异构差分隐私。这种方法充分考虑每个位置点隐私程度，并用数值对隐私保护程度进行描述，使隐私保护结果更加合理和直观。Dwork 等人[22]引入集中差分隐私来控制累积隐私损失，对差分隐私参数的选取做了深入讨论。文献[23]将马尔科夫博弈与差分隐私相结合，以更准确地找出需要保护的位置点并进行相应的隐私保护。Li 等人[24]认为生成的随机和无界噪声并不能完全实现差分隐私，因此提出了有界噪声生成算法和轨迹合并算法，有效提高了隐私保护效率。文献[25]提出了将轨迹分割为较短的新轨迹的方法，该方法适用于处理较长的轨迹数据。文献[26]提出LMDP（Lagrange multiplier-based differentially private）算法对隐私预算进行优化，经过保护后的轨迹数据能防止攻击者通过两位用户的轨迹数据推测出其社会关系。文献[27]基于稀疏位置攻击和最大运行速度攻击，采用构造噪声四分树和R-树分割隐私预算。文献[28]根据地理空间拓扑关系和马尔科夫概率转移矩阵提出了一种基于时空相关性的保护方法。

以上方法从噪声生成方法或考虑轨迹中位置点敏感度并对所有位置点加入不同程度噪声的角度实现轨迹数据保护，对轨迹中位置点进行扰动时均忽略不同位置点间隐私程度的差异，即其假设所有位置点都会泄露用户隐私。且并非轨迹中所有位置点都需要进行隐私保护，否则将导致数据可用性过低，无法保证LBS 的服务质量。由于用户的某些行为模式与习惯能够通过挖掘用户长时间停留的位置点或区域获得，因此对这些位置点和区域的保护就显得极为重要，应选取轨迹中最需要进行隐私保护的部分位置点和区域进行保护。

本文方法充分考虑轨迹中所有位置点间的时序性及相互关系，找出频繁驻留点并对其进行保护，使得攻击者无法从多个位置点间相互关系推测用户隐私。相较于现有的对整条轨迹上所有位置点保护的方法，本文对轨迹中部分特殊位置点和区域进行保护研究，并在特殊的部分位置点上实施差分隐私保护。

4 研究方法

本文方法主要研究内容如图2 中虚线框所示，主要包含数据预处理、挖掘频繁驻留点和基于频繁驻留点的加噪三部分。首先将轨迹数据进行精简，在基本保持轨迹时序性的基础上过滤冗余位置点，同时删除敏感位置，对用户隐私进行保护。数据预处理后，找出轨迹中频繁出现的驻留点，并找到其所在的所有轨迹中对应的位置，最后利用差分隐私保护机制对频繁驻留点加噪，生成隐私保护后的轨迹数据。

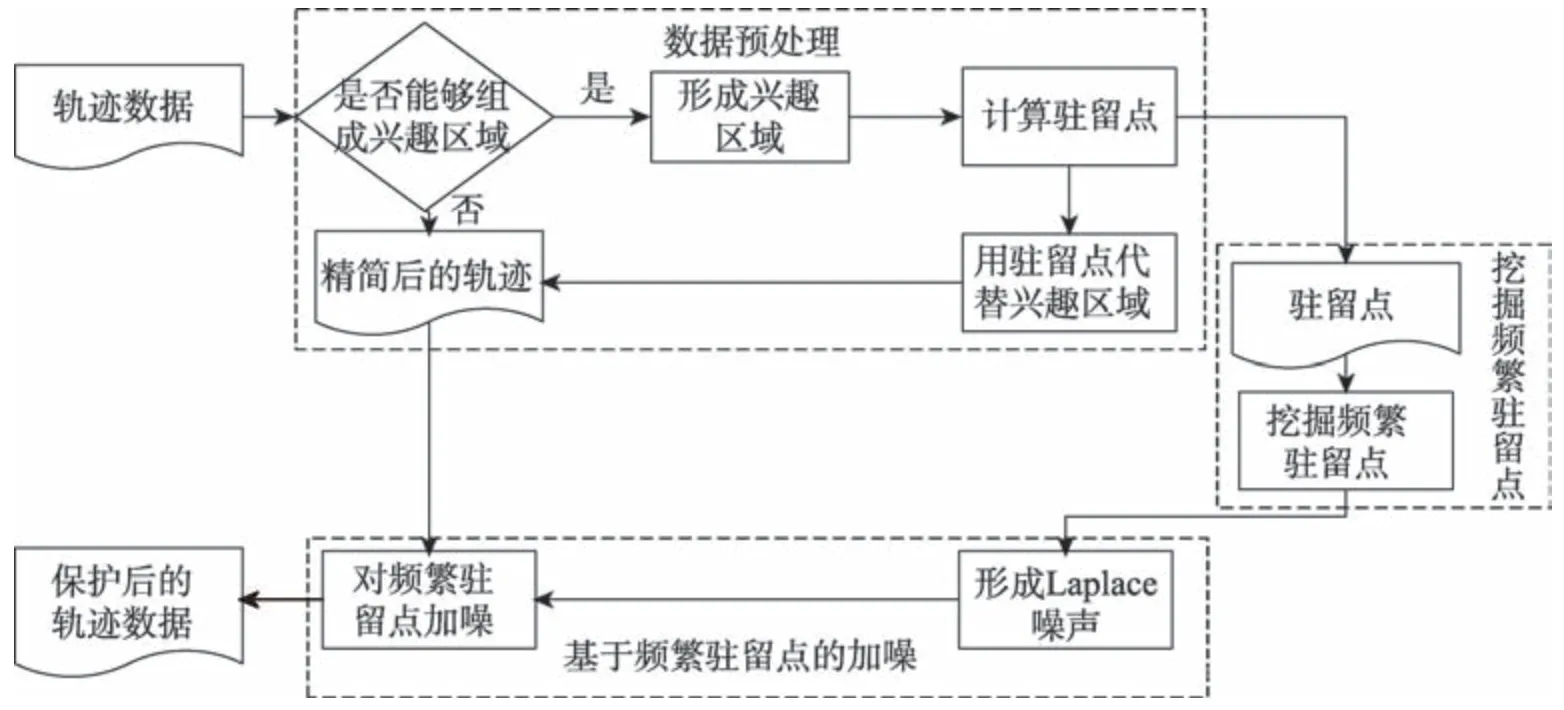
Fig.2 Architecture of this paper图2 本文架构

4.1 数据预处理

4.1.1 兴趣区域及驻留点定义

轨迹是指移动用户的位置信息随着时间变化形成的序列，一条轨迹T是一个GPS 序列，可形式化表示为{(x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn)}，其中(xi,yi,ti),1 ≤i≤n即用户的时空位置，称为轨迹点，也可叫作位置点，表示移动用户在ti时刻所处的位置为(xi,yi)，本文中xi为经度数据，yi为纬度数据，多条轨迹的集合组成了轨迹数据集D。

定义5（兴趣区域）设有轨迹T={(x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn)}，若存在：

称满足上式要求的，从(xi,yi)到(xj,yj),1 ≤i ＜j≤n的移动轨迹序列所形成的区域为用户的兴趣区域。其中ΔS为定义的某个距离阈值，ΔT为定义的某个时间阈值，Distance((xj,yj),(xi,yi))为根据两位置点的经纬度计算得到的两点之间的距离。

定义6（驻留点）轨迹T={(x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn)},假设子轨迹Tr={(xi,yi,ti),(xi+1,yi+1,ti+1),…,(xj,yj,tj)}为用户的兴趣区域，称,的位置点(xm,ym)为该兴趣区域的驻留点。

值得说明的是，对ΔS和ΔT的取值将直接影响兴趣区域的大小和数量，本文将在5.3 节详细讨论针对不同阈值选取对算法表现的影响。

4.1.2 挖掘兴趣区域

轨迹数据的生成与位置点的采集时间有关，如果采集位置数据的时间间隔过短，例如每隔一秒就采集一次数据，将导致生成的轨迹数据量过大，且用户频繁且长时间停留的区域容易暴露用户的行为模式。对于一个连续的GPS 移动轨迹，本文通过定义兴趣区域，挖掘出用户在一定距离范围内停留了一段时间的区域，然后用驻留点代表此区域，同时从此原始轨迹中删除该区域中所有的位置点，以达到避免信息冗余和保护用户隐私的目的。

根据定义5，找出一条轨迹上的兴趣区域的核心是计算出轨迹中停留时间大于一定时间阈值，但距离又限定在一定距离阈值内的轨迹点。

算法主要流程具体步骤如下：首先进行轨迹点之间时间的计算，即从轨迹初始点s=1 开始，依次计算第i个点与初始点s之间的时间差Δt。如果Δt＜时间阈值ΔT，就到达了轨迹的最后一个位置点，则程序结束；如果Δt＞ΔT，则计算从位置s到第i个位置之间的距离Δs。如果Δs＞距离阈值ΔS，则将起点位置s赋值为s+1，按照上述步骤重新计算；如果Δs＜ΔS则首先判断第i个位置是否为结束位置，是则计算从位置s到位置i的驻留点，否则计算第i+1 个位置与位置s之间的Δs′。若Δs′＞ΔS，则计算从位置s至位置i的驻留点；若Δs′＜ΔS，则赋值i=i+1 继续计算从位置s到位置i之间的距离，直至Δs′＞ΔS为止，计算驻留点，并判断i是否为终点位置。如果是则程序结束，否则将当前位置i设为下一次循环的初始位置s，重新开始进行计算。挖掘兴趣区域并找出驻留点后，用驻留点代替兴趣区域覆盖的原始位置点，并更新轨迹。算法如下：

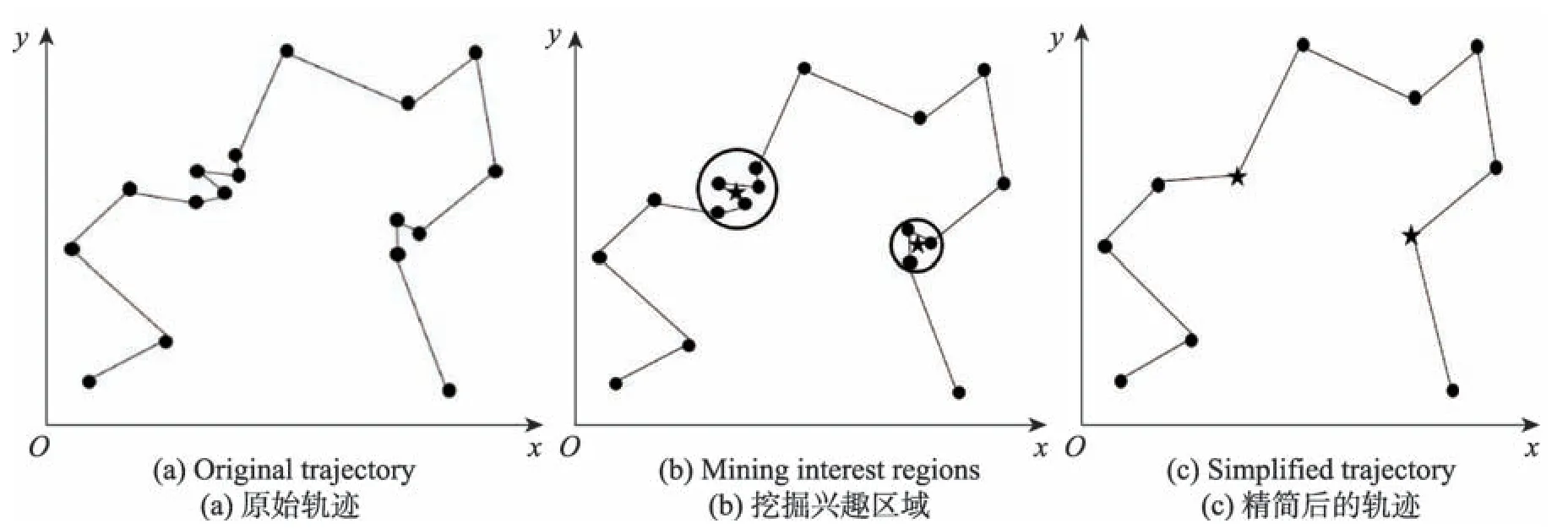
Fig.3 Processes of mining interest region and simplifying trajectory图3 挖掘兴趣区域及精简轨迹过程

假设已有一条用户运动轨迹，如图3（a）所示，实心圆点代表位置点，两点间直线代表行走路线。根据算法1，首先从第一个位置点开始遍历，依次判断其与之后的位置点是否可组成兴趣区域。若否，则将该位置点直接存入精简轨迹；若是，则将满足条件的所有位置点划分为一个兴趣区域，然后计算驻留点，如图3（b）所示，圆圈内区域即为兴趣区域，实心五角星为驻留点。驻留点存入精简轨迹，进行下一次遍历。遍历完轨迹中所有位置点后即可得到精简后的轨迹，如图3（c）所示。

4.2 挖掘频繁驻留点

定义7（频繁驻留点）设通过算法1 得到驻留点数据集P{(x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn)}，若存在Pi=(xi,yi,ti)的出现次数Occ≥θ，θ为支持度阈值，则称Pi为频繁驻留点。

4.3 基于频繁驻留点的加噪

在挖掘出频繁驻留点后，设有频繁驻留点数据集Q{(x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn)},依次遍历Qi,i=1,2,…,n，首先找到Qi所在轨迹及其在轨迹中所处位置，产生服从Laplace 分布的随机噪声LatitudeNoise和LongitudeNoise，将噪声依次加入xi和yi，最后用加噪后的位置点替换原始位置点。

5 实验验证

5.1 实验数据

本文实验首先使用微软亚洲研究院的Geolife[29-31]项目提供的开源数据集，该数据集包含18 670 条真实用户轨迹，被广泛用于轨迹数据相关研究实验[32-33]。由于原轨迹数据记录位置时间间隔过短，导致位置点间距离过近，本文首先采取了每隔5 min 读取一次位置点的方式对原轨迹数据进行精简。

5.2 评价标准

在面向数据发布的轨迹隐私保护研究中，数据可用性和隐私保护程度是两个主要的衡量指标。

5.2.1 数据可用性

数据可用性是对能否从保护后的数据中挖掘出有效信息的度量。针对不同的应用场景，出现了很多不同的数据可用性评价标准，如扭曲度[34]、轨迹相似性度量方法[35]、DTW 距离（dynamic time warping distance）[36]等。由于DTW 距离允许时间序列在局部缩放来最小化两序列之间的距离，其能够更好地匹配时间序列的特点使其被广泛采用[37-40]，因此本文采用DTW 进行数据可用性度量。

定义8（DTW 距离）设有两条轨迹T{(x1,y1,t1),(x2,y2,t2),…,(xm,ym,tm)} 和，长度分别为m与n，则两条轨迹间的DTW 距离为：

5.2.2 隐私保护度

由Laplace 概率密度函数可知，ε越大，产生的噪声越小，对原轨迹扰动越小，隐私保护度也越小。ε越小，产生的噪声越大，对原轨迹扰动越大，隐私保护度也越大。

5.3 参数设定对算法表现的影响

根据定义5 和定义7 可知，距离阈值ΔS和时间阈值ΔT、支持度θ分别为进行兴趣区域和频繁驻留点挖掘时必要参数，为研究上述3 个阈值选取对算法表现的影响，本节首先对ΔS和ΔT的不同取值进行了分析，然后对支持度θ进行讨论。

5.3.1 距离阈值

图4 选择了10 条轨迹进行展示,分析了时间阈值为10 min 时，距离阈值ΔS的变化对兴趣区域个数的影响。从图4 中可以看出兴趣区域个数与距离阈值并非完全正相关，有时距离阈值大的兴趣区域个数反而小于距离阈值小的兴趣区域个数。在少数轨迹中，距离阈值的改变对兴趣区域个数并未产生影响。

Fig.4 Effect of ΔS on the number of interest regions图4 ΔS 对兴趣区域数量的影响

5.3.2 时间阈值

图5 同样选择了10 条轨迹进行展示，分析了距离阈值为200 m 时，时间阈值ΔT的变化对兴趣区域个数的影响。由图5 可见，时间阈值与兴趣区域个数基本成负相关趋势，时间阈值越大，对应的兴趣区域个数反而越小。这是因为在距离阈值一定的情况下，时间阈值越大，表明用户在某一位置点停留的时间就要越长，这就使该位置点可组成兴趣区域的条件更加严苛，导致兴趣区域个数减少。

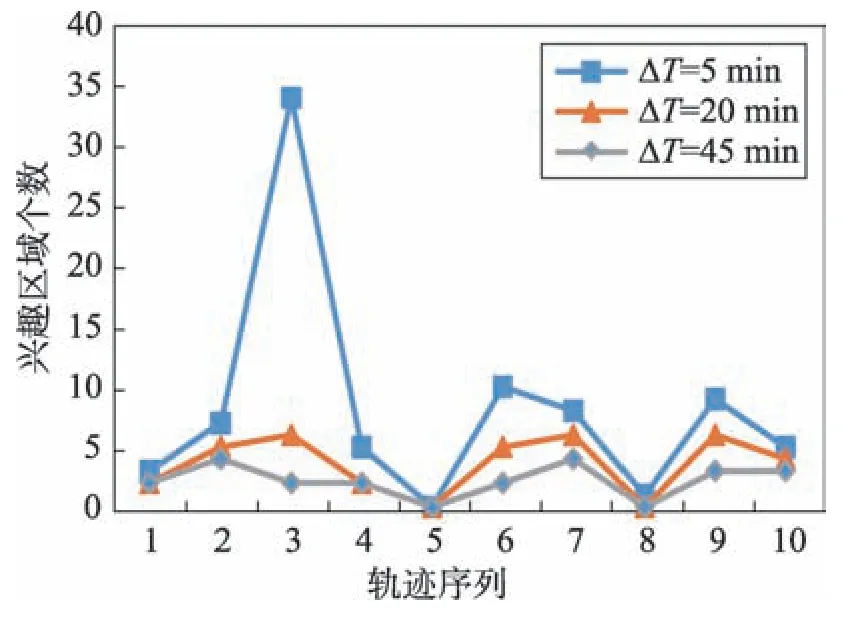
Fig.5 Effect of ΔT on the number of interest regions图5 ΔT 对兴趣区域数量的影响

5.3.3 支持度

支持度θ代表某一位置点出现次数，本文将出现次数大于θ的驻留点称为频繁驻留点。本文对12 位用户一年中所有轨迹数据集使用不同的θ进行实验，结果如图6 所示。在所有用户轨迹中，支持度为2时，频繁驻留点个数最大，支持度为6 时，频繁驻留点个数最小。θ取值增大的同时频繁驻留点个数呈下降趋势。可见支持度越大，频繁驻留点越少。图7 中6条曲线分别为6 位用户一年的轨迹在θ从1 至5 的情况下各自对应的平均失真度。从图7 中可以看出，θ值越大，平均失真度越小。这是因为θ越大，即频繁驻留点的条件越苛刻，满足出现次数大于θ的驻留点就越少。因此在加噪时，扰动的位置点也就越少，失真度也随之减小。

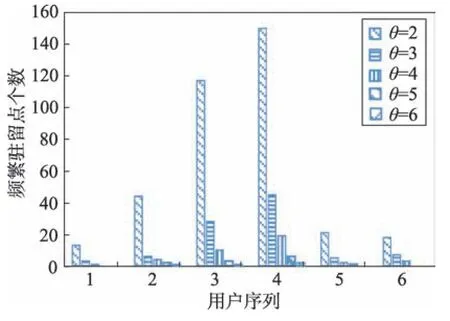
Fig.6 Changes in the number of frequent-stay points图6 频繁驻留点数量变化

Fig.7 Changes in average distortion图7 平均失真度变化

5.4 实验结果及分析

为验证本文所提方法性能，将文献[19]中提出的Pnoise、Cnoise 和Gnoise 作为基线方法，使用真实数据集进行对比实验。本文实验过程中对不同用户一年中所有轨迹进行实验，但限于文章篇幅，本文仅从中随机选取10 条轨迹进行示例，但完整实验结果与示例轨迹结果分布一致。

5.4.1 数据可用性

本文采用DTW 距离来衡量隐私保护前后轨迹的失真度，并以此来评价轨迹数据的可用性。一般情况下，两条轨迹之间的差异越小，即失真度越小，则实施隐私保护后的轨迹可用性越强。

本文分两种情况对数据可用性进行分析：首先选定时间阈值为10 min，然后选取不同的距离阈值；其次选定距离阈值为200 m，然后选取不同的时间阈值。为进行对比，本文实现了文献[19]中提出的Pnoise、Cnoise 和Gnoise 隐私保护方法，同时计算出实施3 种隐私保护方法后不同轨迹的失真度，并与上述实验设置后所得的本文方法性能结果进行对比。实验结果如图8、图9、图10 所示。

通过观察图8、图9 以及图10 中的图（a）可以发现在ΔT固定的情况下，基本呈现ΔS越小，失真度也越小的趋势。这是因为ΔS越小，兴趣区域可包含的位置点就越少。对原始轨迹中的位置点进行越少的删除，所划分兴趣区域后的精简轨迹与原始轨迹相似度越高，因此在后续挖掘频繁驻留点以及加噪的步骤中造成的信息损失度会小于兴趣区域数量较大时的信息损失度。从图10（a）可发现在第6 条轨迹处，ΔS=150 m 时的失真度高于ΔS=500 m 的失真率，由此可以得出失真度与ΔS并不完全成正比关系。

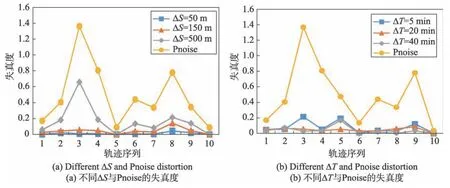
Fig.8 Comparison of Pnoise method and proposed method图8 本文方法与Pnoise 方法对比

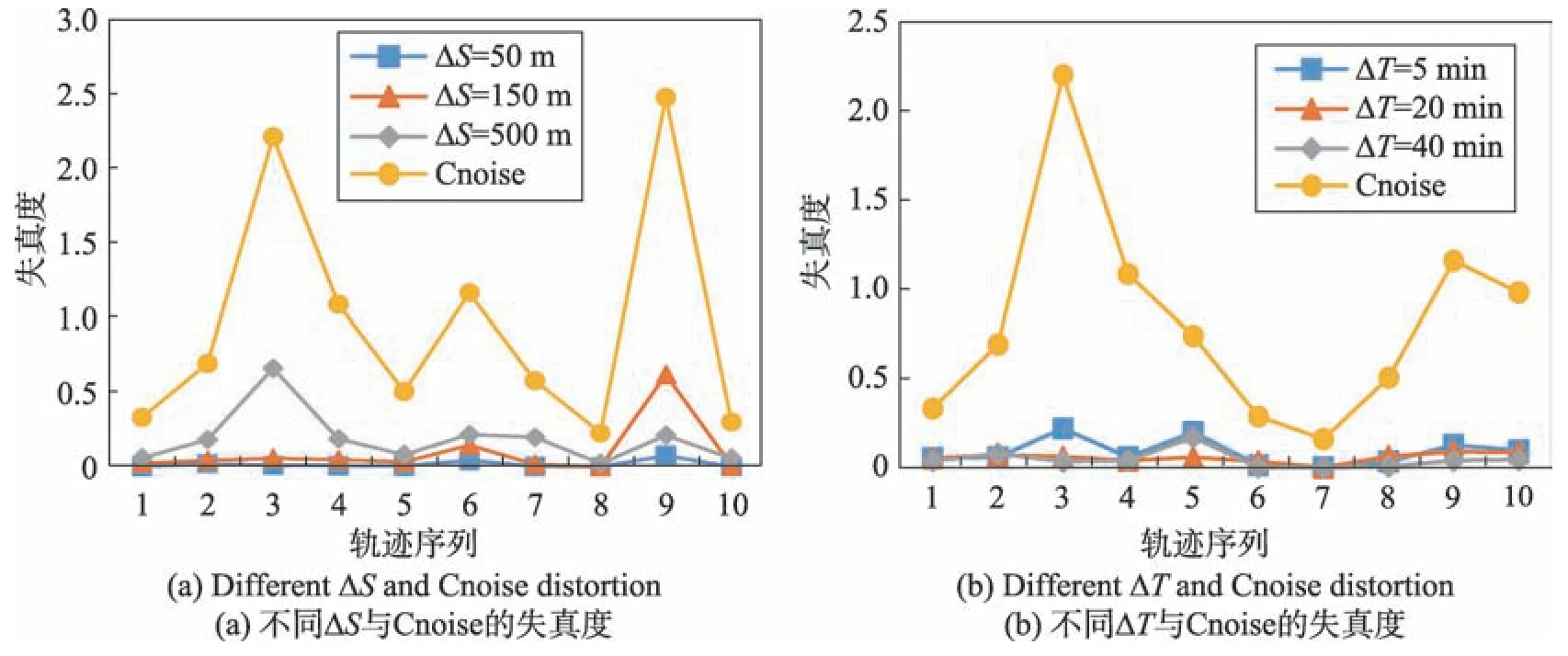
Fig.9 Comparison of Cnoise method and proposed method图9 本文方法与Cnoise 方法对比

Fig.10 Comparison of Gnoise method and proposed method图10 本文方法与Gnoise 方法对比

同时还可明显看出本文方法在取不同阈值情况下，轨迹数据失真度均小于基线方法。尤其在图10（a）中，ΔT=10 min，ΔS=50 m 时，本文方法失真度为0.031 3，Gnoise 方法失真度高达2.341，此时本文方法优越性最为明显。这表明经本文方法保护后发布的轨迹数据在隐私信息得到保护的同时依然具有较高的可用性。

在得到轨迹数据集中所有轨迹的失真度后，将所有轨迹失真度累加后除以轨迹数据集中轨迹的个数即为平均失真度。表1 给出了采用不同方法对某一用户一年中所有轨迹进行隐私保护后得到的轨迹数据集的平均失真度。

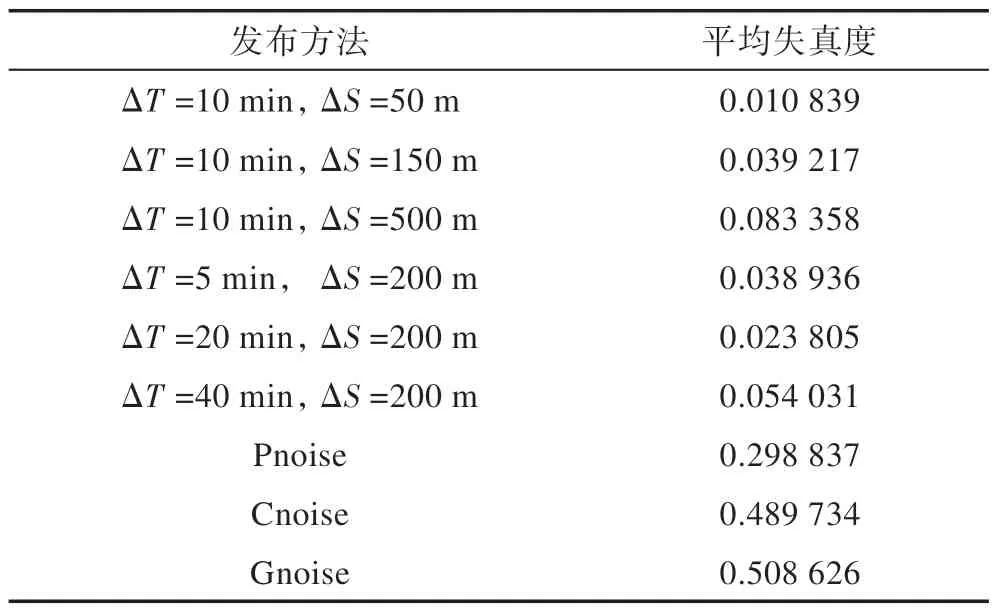
Table 1 Different methods and their average distortion on real world datasets表1 真实数据集上不同方法与平均失真度

在ΔT=10 min，ΔS=50 m 时，本文方法运行结果失真度为0.010 839，基线方法中的Gnoise 失真度则高达0.508 626，高出本文方法0.497 787。这表明经过本文方法保护后的轨迹数据可用性可大幅度高于现有轨迹数据发布方法。纵观表1，本文方法在多种情况下平均失真度均低于基线方法，这再次证明上述3 组对比图结果的正确性。

5.4.2 隐私保护度

本文随机选取3 位用户的所有轨迹，在进行数据预处理、挖掘频繁驻留点后，对频繁驻留点加入不同大小的噪声并计算所有轨迹的平均失真度，以此论证隐私保护性能。根据差分隐私相关定义可知，ε越大，隐私保护度越低，ε越小，隐私保护度越高。

实验结果如表2 所示，从第2 列起每一列分别表示每位用户轨迹在不同噪声值下的平均失真度。从表中可看出，由于ε取值越大，生成的噪声越小，因此ε的取值与3 位用户的轨迹平均失真度成反比。当ε取0.05 时，平均值失真度最大，ε取1 000 时平均失真度最小。这个结果与加入的噪声越大，隐私保护性能越好的结论相符。当ε取0.05和1 000时，用户2轨迹数据平均失真度分别为73.299 32 和0.046 312，差距最大，为73.253 01。观察用户1 轨迹的平均失真度，在ε=5 时，轨迹平均失真度相较于ε=1 时，降低幅度为0.966 12；在ε=10 时，轨迹平均失真度相较于ε=5 时，降低幅度为0.080 074；在ε=100 时，轨迹平均失真度相较于ε=10 时，降低幅度为0.094 967。可见不同ε之间的平均失真度的降低幅度并非持续变小，这是由于不同用户轨迹数据的特殊性以及算法中生成的随机数在一定区间内波动。

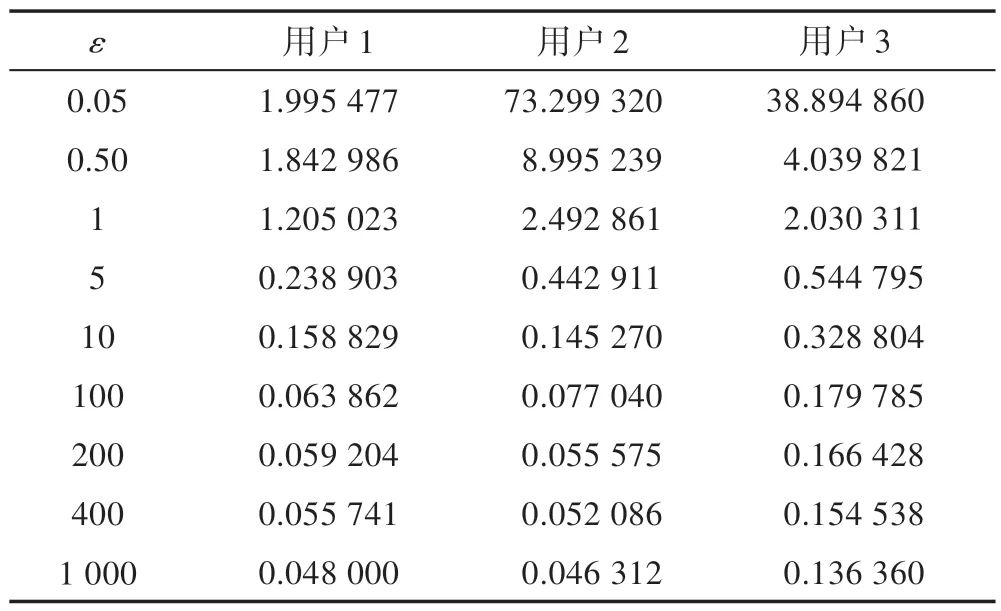
Tabel 2 ε and average distortion on real world datasets表2 真实数据集上ε 与平均失真度

表3 中的实验结果表明，预处理后相较于每隔5 min 读取一次位置点后，位置点个数减少比例最低为34.08%，最高为73.62%。轨迹中位置点数量的减少可降低攻击者可获得的位置信息，加大了攻击者根据已有位置信息推测用户隐私的难度，证明了本文方法轨迹数据隐私保护的有效性。

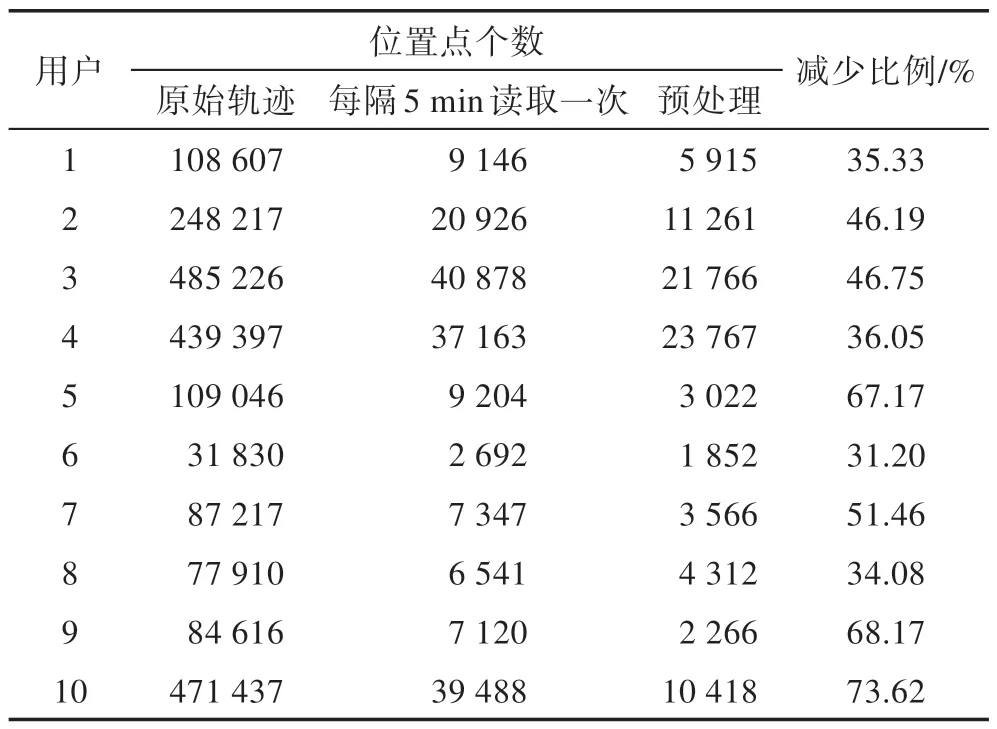
Table 3 The number of locations in different phases表3 不同阶段位置点个数

5.5 仿真数据实验

为进一步验证本文方法有效性，本文使用轨迹数据相关研究领域[27,41-42]常用的Brinkoff 模拟器生成了15 000 条用户轨迹，对本文方法进行了仿真实验。随机抽取部分实验结果进行展示，展示结果与完整实验结果趋势相同。

表4 展示的为本文方法在相同ΔT，不同ΔS的情况下，与3种基线方法的平均失真度。由于Brinkoff生成的坐标均为模拟坐标，因此仿真实验中使用的距离均为模拟地图上的相对距离，故表4 中的ΔS无具体距离单位。本文方法在相同ΔT，不同ΔS时，平均失真度波动小，但3 种情况下的平均失真度均小于3 种基线方法。最为显著的是，当ΔT=5 min，ΔS=490 时，本文方法平均失真度相较于Cnoise，平均失真度降低了0.655 263。

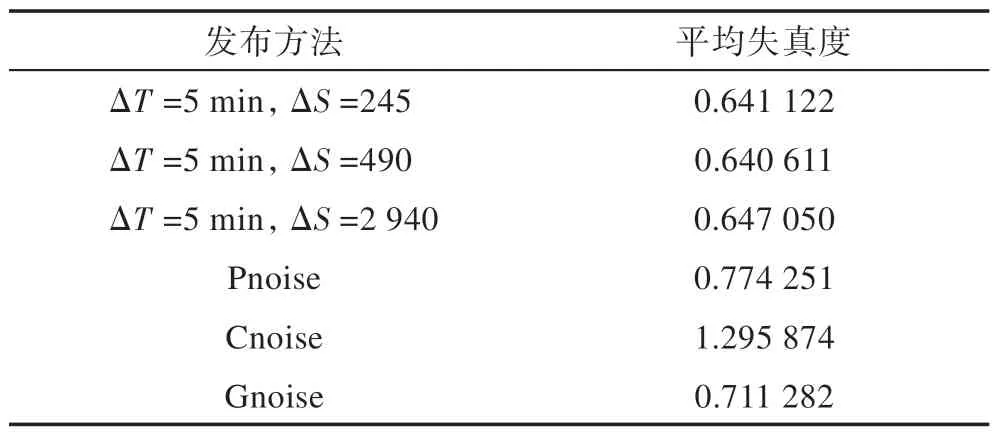
Table 4 Different methods and their average distortion on simulation datasets表4 仿真数据集上不同方法与平均失真度

表5 展示的为在不同ε的情况下，经本文方法处理后3 位用户轨迹的平均失真度。从表中可看出，随着ε的增长，3 位用户轨迹的平均失真度均随之降低，与表2 具有相同的趋势。

Tabel 5 ε and average distortion on simulation datasets表5 仿真数据集上ε 与平均失真度

综上可知，无论是在真实轨迹数据集或仿真轨迹数据集上，在保护轨迹数据隐私的前提下，本文方法相较于现有方法均有效提高了轨迹数据的可用性。

6 结束语

轨迹数据发布方法一直是隐私保护的研究热点，针对现有方法中将轨迹中所有位置点进行保护导致数据可用性降低的问题，本文提出了一种融入兴趣区域的差分隐私轨迹数据保护方法。该方法划分兴趣区域挖掘出驻留点，并通过差分隐私机制对频繁驻留点进行隐私保护。达到通过对部分位置点进行保护，在保护数据隐私的前提下保证数据可用性的目的。通过对真实轨迹数据集和仿真轨迹数据集进行实验，验证了本文方法的有效性。在真实轨迹数据集上，当ΔT=10 min，ΔS=50 m 时本文方法与Pnoise、Cnoise 和Gnoise 三种基线方法相比，将平均失真度分别降低了0.287 998、0.478 895 和0.497 787；在仿真轨迹数据集上，当ΔT=5 min，ΔS=490 时，本文方法与Pnoise、Cnoise 和Gnoise 三种基线方法相比，将平均失真度分别降低了0.133 640、0.655 263 和0.070 671。同时，实验中通过调整ε的取值可控制隐私保护的性能，ε的取值从0.05 增长至1 000 的过程中隐私保护性能逐步降低。在挖掘兴趣区域时，对原轨迹进行精简的步骤也对轨迹数据进行了隐私保护。实验结果表明，相较于现有的在所有轨迹数据上进行加噪的隐私保护方法，本文方法虽只在部分轨迹数据上加噪，但在保护轨迹数据隐私的前提下，提高了数据可用性。

由于轨迹数据本质上是实数序列，不同轨迹具有自身特性，使得本文方法还存在部分问题有待探讨，如还需找到更具普适性的兴趣区域相关阈值等。同时由于驻留点代替的为一定区域，因此本文在挖掘频繁兴趣驻留点时对数据精度进行了适当调整。这些问题为将来的研究指出了方向，为进一步验证本文方法的有效性，也为提高本文方法普适性，将对本文方法进行更深入的研究和改进。