混合互信息和粒子群算法的多目标特征选择方法*
2020-01-11王金杰
王金杰,李 炜
1.安徽大学 计算机科学与技术学院,合肥230601
2.安徽大学 计算智能与信号处理重点实验室,合肥230039
1 引言
在机器学习和数据挖掘中,分类是一个很重要的任务。在没有先验知识的情况下,很难决定哪个特征是有用的,导致了数据集中包含了相关的、不相关的以及冗余的特征。在进行分类时,由于不相关的和冗余的特征带来的维度灾难,不仅没用,而且还会降低分类性能[1]。特征选择通过选出具有代表性的特征子集,提高了算法效率,减少了计算开销,同时避免了过拟合问题,提高了泛化能力[2]。特征选择技术主要分为三类:过滤式、封装式以及嵌入式[3]。过滤式方法先通过对数据集进行特征选择,然后再进行训练学习。而封装式方法直接把最终将要使用的学习器的性能作为特征子集的评价标准。嵌入式方法则是将特征选择过程与学习训练过程融为一体,两者在同一个优化过程完成。
特征选择有两个最主要的冲突:最小化分类错误率和最小化特征个数,故可以将特征选择看成一个多目标问题。由于PSO(particle swarm optimization)算法具有较小的计算花费以及快速的收敛优点,其是特征选择中一个有效的技术方法[4]。Xue 等人曾在2013 年提出了一篇基于拥挤距离(crowding)、突变策略(mutation)和支配关系(dominance)的PSO 算法的多目标方法,命名为CMDPSO[5]。通过该方法能获得一个较好的特征子集的集合,然而仍然有很大的潜力去探索和提升帕累托前沿面;Nguyen 等人在2016 年提出了基于PSO 用相似距离来选取gbest以及更新Archive 的多目标特征选择方法MOPSO-SiD(multiobjective particle swarm optimization using subset similarity distance)[6]。该方法在一定程度上提升了帕累托前沿面,但是由于没有较好提升种群的探索能力,导致当种群迭代到后期时还是容易陷入局部最优;在2016 年,Nguyen 等人在CMDPSO 算法的基础上进行改进,通过一个局部搜索策略包括插入(inserting,I)、交换(swapping,S)和删除(removing,R)三个操作去提升外部文档集合,提出一个新的Archive 机制的ISRPSO 算法[7]。虽然通过该机制获得了更好的分类性能,但是本质上并没有改进种群本身,而且花费了大量的计算代价在评估上。近些年来也有越来越多的人提出了基于差分进化算法(differential evolution algorithm,DE)的多目标特征选择方法[8-9],以及基于人工蜂群算法(artificial bee colony algorithm,ABC)的多目标特征选择方法[10-11]等,并且也在不断完善。
除此之外,早在2009 年,Estévez 等人提出了一个将互信息与遗传算法(genetic algorithm,GA)相结合的特征选择的方法GAMIFS(genetic algorithm mutual information feature selection)[12]。该方法利用互信息改进种群的初始化以及利用NMIFS(normalized mutual information feature selection)标准提出了一个突变操作,克服了类似mRMR(minimal redundancy maximal relevance)增量搜索算法的限制,同时还在一定程度上提升算法的探索能力。在2015年Butler-Yeoman等人提出了两种基于粒子群优化(PSO)的过滤式-封装式混合特征选择算法:第一种算法FastPSO 将过滤式和封装式方法结合到PSO 的搜索过程中进行特征选择,大部分评价为过滤式方法,少量评价为封装式方法;第二个名为RapidPSO 的算法进一步减少了封装式方法的计算数量[13]。但是提出的两种方法与封装式PSO 算法比较获得相似的分类性能,时间也较短,但是特征数量更多;同时与传统的启发式搜索方法相比也没有解决特征数量较多的问题。Tran 等人在2016 年利用互信息对粒子的pbest进行更新,但是该方法是一个针对高维度数据集进行分类的方法[14]。在2017 年,Nayak 等人提出了将DE 和MI(mutual information)相结合的具有有效冗余度量的过滤方法[15]。虽然该方法的评估标准优于文中提出的对比方法,但是由于每代种群的产生都是由父代种群和子代种群结合通过精英策略产生,种群在迭代早起失去了多样性,容易导致过早收敛的问题。在2018年,Hammami 等人提出了一篇基于GA 和MI 的FW-NSGA-II(filter-wrapper-based nondominated sorting genetic algorithm-II)混合的多目标特征选择算法[16],使用一个基于指标的多目标局部搜索(indicator based multiobjective local search,IBMOLS)方法去提升种群的非支配面等。
综合上述文献,本文针对粒子群容易陷入早熟的特点提出一个自适应突变策略去扰动种群,同时为了获得更好的非支配面集合,本文利用粒子群算法的全局搜索能力卓越的优点和互信息自身的特点去平衡种群的全局和局部搜索。
2 背景介绍
2.1 PSO 算法
PSO 算法是模仿了一群鸟儿在飞行时相互交流,每只鸟都有一个特定的方向,当它们在一起交流时,它们会识别出最佳位置的鸟。然后,每只鸟从新的局部位置调查搜索空间,然后重复这个过程,直到鸟群到达预期的目的地。这一过程包括鸟类从它们自己的经验(局部搜索)中学习和从它们周围的其他鸟(全局搜索)的经验中学习[17]。
在传统的PSO 中,种群是由粒子集合组成,每个粒子都代表一个优化问题潜在的解。在种群中,把第t次迭代产生的第i个粒子的位置表示为:
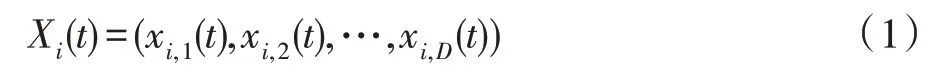
第t次迭代产生的第i个粒子的速度表示为:
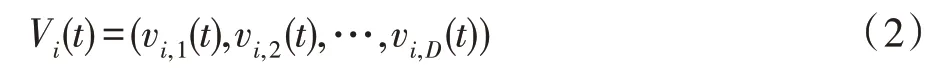
在t+1 代粒子的速度和位置根据式(3)和式(4)两个公式进行更新:
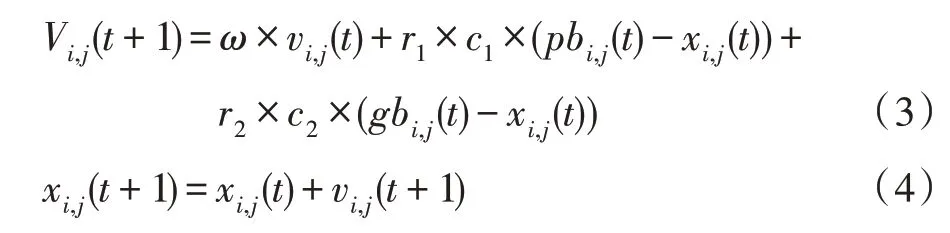
pbesti表示第i个粒子目前最好的位置,gbest表示所有粒子目前为止发现的最好的位置。加速系数c1和c2是控制pbest和gbest对搜索过程影响的非负常数;ω表示控制粒子在搜索空间中的探索的惯性权重。r1和r2是[0,1]内的两个随机值。
2.2 互信息
在概率论和信息熵领域中,互信息是用来测量两个变量之间的依赖性的方法。两个随机变量X和Y之间的互信息可以被表示为:
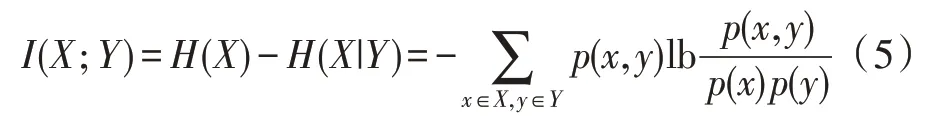
其中,H(X)是随机变量X的熵;p(x,y)为联合概率质量函数;p(x)和p(y)为边缘概率。X和Y之间关系越紧密,I(Xi;Y)的值越大,如果两个变量之间相互独立,则I(Xi;Y)的值为0。
将互信息应用在特征选择问题上时,当随机变量X表示粒子特征,随机变量Y表示标签时,I(Xi;Y)计算出的值表示粒子和标签之间的相关性,值越大,特征与标签之间的相关性越大,反之越小。如果变量X和Y都表示特征,I(Xi;Y)计算出的值表示粒子之间的冗余性,值越大,特征之间的冗余性越大,反之越小。
在基于互信息的特征选择研究上,Peng 等人[18]提出了最小冗余性最大相关性(mRMR)评估标准,其目标函数定义为:
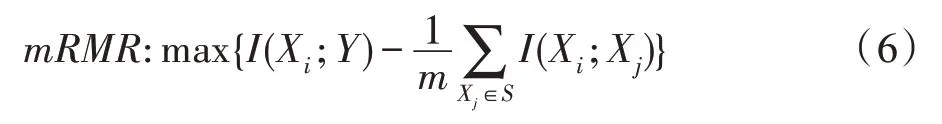
其中,m是已选特征子集S的特征个数,Xi为第i个候选特征。对于顺序向前搜索的方法,每次从候选集中加入一个式(6)值最大的特征进入已选特征集中,直到满足停止标准为止。
由互信息的定义可以得出:
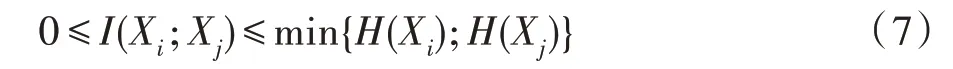
Vinh 等人基于上式,重写了式(6),使得对式(6)里两个子项都进行了标准化[19]。
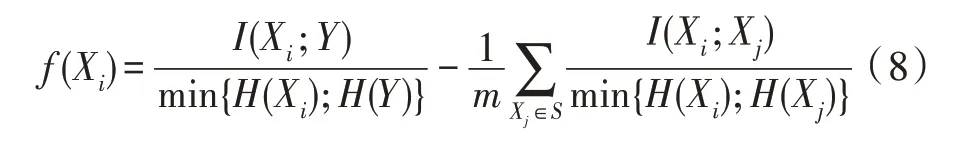
2.3 多目标优化
多目标优化一般涉及到最大化或者最小化多个冲突目标函数。用数学术语,最小化多目标函数的公式可被写为[5]:
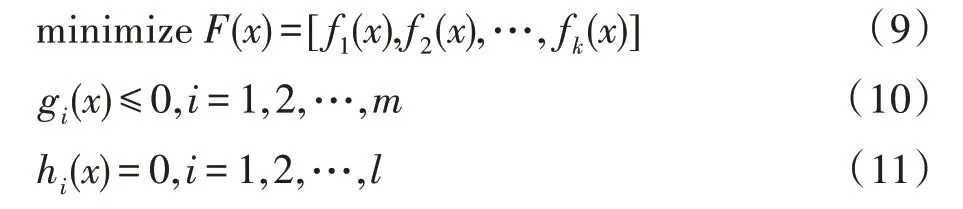
其中,x是决策变量,fi(x)是x的函数,k是最小化的目标函数的个数,gi(x)和hi(x)是问题的约束条件。
假设y和z是k个目标最小化问题的两个解,如果满足:
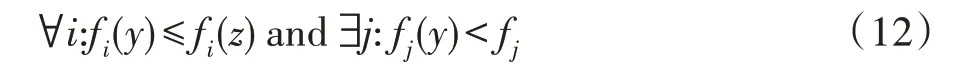
其中,i,j∈{1,2,…,k}。那么称y支配z。
对于两个目标的问题,如图1。
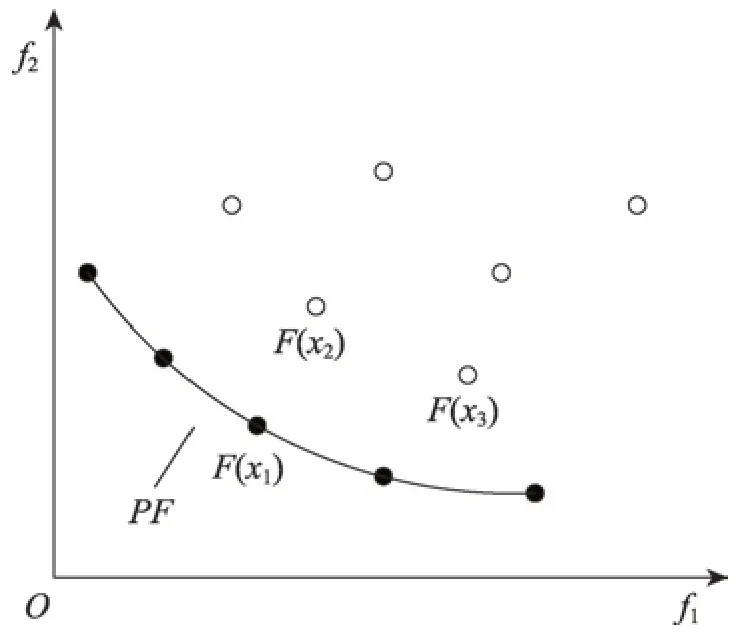
Fig.1 Minimization problem with two objective functions图1 两个目标的最小化问题
x1支配x2和x3,而x2既不支配x3,x3也不支配x2,故x2和x3互不支配。当一个解不受其他解支配时,称为帕累托最优解(Pareto)。在搜索空间中,所有帕累托最优解的集合形成了平衡曲面,称为帕累托前沿面(Pareto front,PF)。利用多目标优化算法能够去探索非支配解集。
2.4 特征选择
特征选择是一种典型的组合优化问题,其从N个特征集合中选出M个特征的子集(M≤N),去除冗余或不相关的特征,使得处理后的数据集不仅包含的特征个数更少,而且能够提高分类算法在原有特征集合的分类性能[20]。
特征选择中主要的两种方法:过滤式和封装式。如图2 所示[21],过滤式方法是对数据集本身进行评价(如互信息)。封装式方法直接把最终将要使用的学习器的性能作为特征子集的评价标准(如粒子群),如图3 所示[21]。
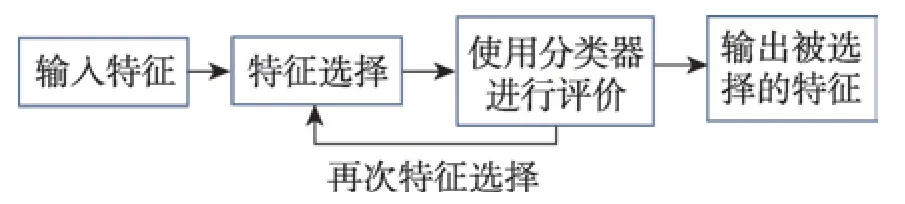
Fig.2 Filter feature selection图2 过滤式特征选择

Fig.3 Wrapper feature selection图3 封装式特征选择
3 基于混合PSO 和MI 算法的多目标特征选择方法
3.1 基于互信息方法的局部学习策略
3.1.1 外部文档和非支配面的集合概念
由于外部文档(Archive)中存放的是到目前为止所迭代产生的最优解。在每次迭代时,粒子群算法会在外部文档中选择一个gbest用来指引粒子的飞行。因此,在Archive 中的每个粒子都很重要。同时Archive成员选择的特征可以被视为重要特征。
Archive 中的第i个粒子的已选特征集合定义为A_Si,则未选择的特征集合定义为A_USi。假设特征维度为8,可表示为{f1,f2,f3,f4,f5,f6,f7,f8}。Archive中包含3 个非支配解Archive={A1,A2,A3},根据上面的集合定义,Archive 中3 个解对应的A_Si和A_USi集合可表示为:
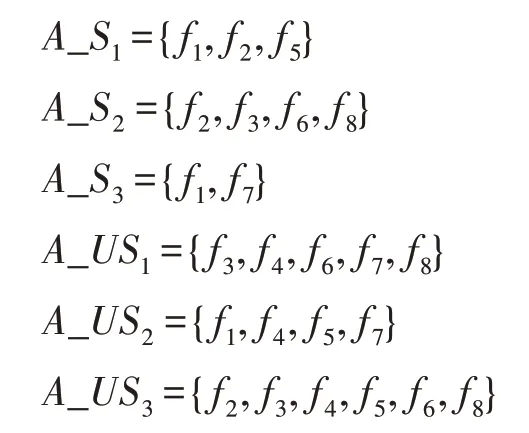
同时种群每次迭代都会产生PF,里面存放着当前种群的非支配解的集合。故PF 里面的第j个粒子的已选特征集合定义为F_Sj,则未选择的特征集合定义为F_USj。假设PF 中包含3 个粒子,根据上面的集合定义,PF 中3 个粒子对应集合可表示为:
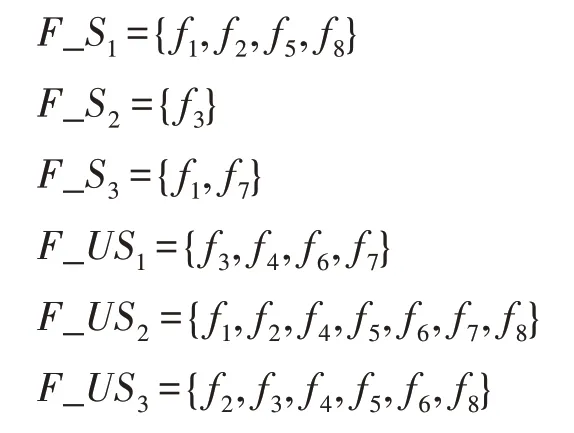
根据上面定义的两个集合概念,再结合差集运算,本文定义以下几个关系概念。
定义1(>)假设有集合A和集合B,AB不为空,BA等于空,则集合A大于集合B。例如:
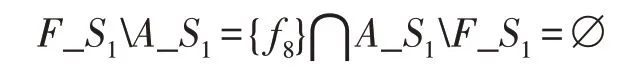
称F_S1大于A_S1。
定义2(<)如果AB等于空,BA不为空,则集合A小于集合B。例如:
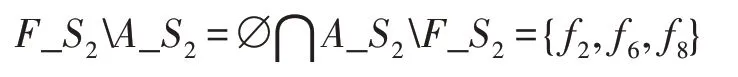
称F_S2小于A_S2。
定义3(=)如果AB等于空,BA等于空,则集合A等于集合B。例如:

称F_S3等于A_S3。
定义4(<>)如果AB不为空,BA不为空,则集合A与集合B互不包含。例如:

称F_S1与A_S2互不包含。
3.1.2 基于互信息的插入删除操作
当种群每一次迭代时,对种群产生的PF 中的第j个粒子(particlej),本文采用随机选择策略从Archive中选择一个引导粒子(lead)。本文对particlej进行插入删除操作规则如下:
(1)如果particlej已选的特征集合F_Sj小于lead已选择的特征集合A_Slead,则认为lead中含有particlej没有选择的相关特征。particlej插入仅存在lead中的特征Set_Only_In_A_Slead=A_SleadF_Sj。
(2)如果F_Sj大于A_Slead,则认为particlej可能选择一些不相关和冗余的特征,因此删除lead中没有选的特征Set_Only_In_F_Sj=F_SjA_Slead。
(3)如果F_Sj和A_Slead两个集合是相等的或者互不包含的,随机选择插入操作或者删除操作。①假如两个集合是相等的,如果是插入操作,则插入的特征是particlej中没有选择的特征F_USj,如果是删除操作,则删除particlej中已选择的特征F_Sj。②假设两个集合互不包含,如果是插入操作,particlej插入仅存在lead中的特征,如果是删除操作,则particlej删除仅自己选择而lead没有选择的特征。
对粒子插入删除的特征个数受多个因素限制,包括particlej已选的特征个数,lead已选的特征个数等。故本文对于粒子插入删除的特征个数设置了一个最大值,这个最大值是根据粒子的维度以及百分比α来决定的。
Insert:将式(6)计算得出的结果称为Relevant,对于粒子的插入操作,插入Relevant 值最大的特征f。如果插入的特征个数大于1,则将刚插入的特征f加入已选特征集中,从候选特征集中删除特征f,再重新计算Relevant,继续进行插入操作。
Delete:对于粒子的删除操作,定义两个公式:

其中,US为将要删除的特征集合。(1)如果选择删除不相关的特征,则利用式(13)计算待删除的特征集合对应的Irrelevant 值,其中Irrelevant 值最小的特征被定义为最不相关的特征,将其删除。(2)如果删除冗余特征,通过式(14)计算对应的Redundant 值,找到最大Redundant 值,其值对应的是两个特征之间的相关性,再利用式(13)计算这两个特征的Irrelevant值,删除Irrelevant值最小的特征。
3.1.3 精英策略
Deb 在2002 年提出了快速精英策略的多目标遗传算法[22]NSGA-II。文章将父代种群和子代种群相结合,通过精英策略产生新的父代种群。实验证明精英策略可以加速算法的执行速度,由于该策略扩大了采样空间,在一定程度上确保己经找到的最优解不会丢失。
故本文将PF 的粒子通过互信息进行插入删除操作后得到新的粒子集合,通过将两个粒子集合进行合并,使用精英策略能够保留最优的粒子,不仅能改善PF,还能优化Archive。同时采用拥挤距离进行比较,能够使得PF 中的粒子均匀分布,保证种群的多样性。
算法1 是针对本文提出的局部搜索算法的伪代码。第2 行MaxChangeNum表示粒子改变维度的最大个数,第31 行的Container是一个集合,用来存放每次学习后的粒子。第6~12 行根据3.1.1 小节介绍的集合概念计算PF 中的粒子i和Archive 中的粒子lead对应的集合,lead是在外部文档中随机选择的一个引导粒子,第14~32 行对粒子进行插入删除操作,第33 行利用精英策略进行筛选,获得更好的PF。


3.2 自适应突变操作
粒子群算法具有较快的收敛速度。然而,快速的收敛速度往往使基于粒子群的算法收敛到错误的PF 中。然而已研究的文章较多是通过基因算法中的突变操作来解决的,而突变概率是不变的。针对种群中每个粒子,并不都是随着迭代次数增加而陷入停滞,故本文针对种群中每个粒子采用非线性函数Pm自适应控制每个粒子的突变概率和突变范围,来扩展该算法在勘探中的应用能力。
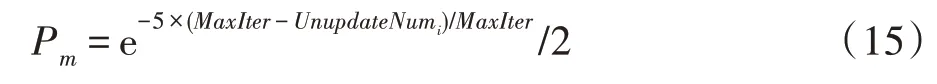
其中,MaxIter代表最大迭代次数,UnupdateNumi表示第i个粒子当前的pbest距离其上一次pbest更新的次数。可以看出,随着迭代次数增加,种群越容易陷入局部最优,导致粒子对应pbest不能更新,Pm的值随着UnupdateNum增加,趋向于以指数增加。如算法2 所示:如果rand<Pm,对当前粒子执行突变,rand∈[0,1]。首先从该粒子中随机选取k个元素,然后在搜索空间中重新初始化相应维度的值。这里k的值是用于控制突变范围的整数。
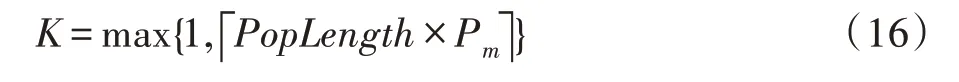
其中,Poplength表示粒子的维度。
3.3 gbest的选取
在Archive 中,粒子的拥挤距离越大,表示解空间中,在该粒子局部范围内分布的粒子越少。本文通过二进制锦标赛的方法,从Archive 中选择两个粒子。再比较两个粒子拥挤距离,选择拥挤距离大的粒子作为gbest。通过该方法选择gbest能够使得种群在不断的迭代中获得更均匀,分布性更好的PF。
3.4 Archive的更新
每次迭代后,将种群的PF 加入Archive 中,通过支配和非支配关系,将被支配的解全部从Archive 中删除,保留非支配解。如果非支配解的个数超出Archive 的大小,则根据拥挤度依次从小到大从Archive中删除粒子,直到满足条件为止。


3.5 种群的编码、解码与评价
对于种群中的每个粒子,其位置向量每一维均表示为0~1 之间的实数。根据特征选择问题的特殊性,设置一个阈值Threshold,如果位置向量某个维度的值大于阈值Threshold,则表示对应维度的特征被选择;反之,如果小于阈值Threshold,则表示对应维度的特征未被选择。
本文采用在特征选择中最普遍的两个相互矛盾的目标函数:特征子集中的特征数目和对应的分类错误率。其中,在相关文献中[23-24],采用分类错误率作为适应度函数直接对粒子进行评价。分类错误率按式(17)计算:
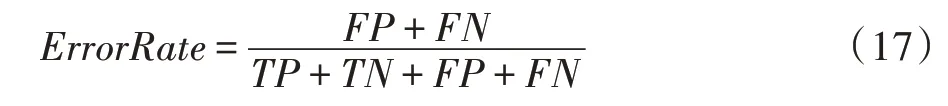
其中,FP表示负样本被预测成正样本的个数,FN表示正样本被预测成负样本的个数,TP表示正样本被预测成正样本的个数,TN表示负样本被预测成负样本的个数。
图4 为本文算法流程图。
4 实验设计和结果分析
为证明本文提出的基于混合PSO 和MI 的多目标特征选择方法的有效性和优越性,首先将提出的HMIPSO 方法与MOPSO 算法以及Xue 等人在2013年提出的经典的CMDPSO 算法进行对比[5],证明了本文提出的HMIPSO 方法能有效改善PSO 算法在多目标特征选择应用上的性能;然后还比较了NSGA-II算法[22]以及在2017 年由Hancer 等人提出的基于人工蜂群算法的帕累托面特征选择方法[11],本文对比的是Hancer 提出的BMOABC(binary multi-objective artificial bee colony)算法。实验结果证明了本文提出的方法比传统的方法和最新的技术方法在性能上都有提升。本文所有实验均在内存16.0 GB 的PC 机上运行,运行环境为Matlab R2016b。
4.1 数据集和实验参数设置

Fig.4 Flow chart of HMIPSO图4 HMIPSO 算法流程图
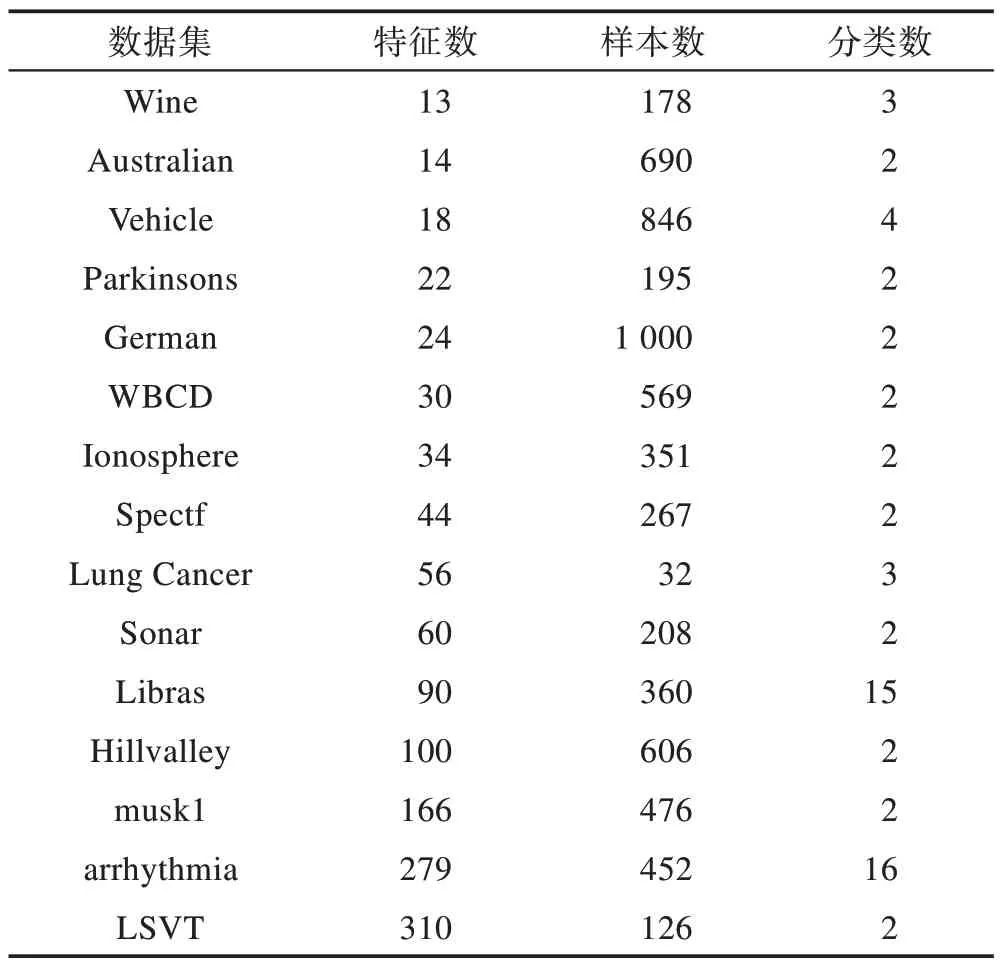
Table 1 Information of datasets表1 数据集信息
表1 是在本次实验中使用到的15 个数据集,是从UCI 机器学习库中选择出来的。这些数据集的特征个数从Wine 最小的13 个到LSVT 最大的310 个,样本个数从Lung Cancer 最少的32 个到German 最多的1 000 个,具有充分的代表性。因此对算法的优化能力提出了很高的要求。
在进行实验时,每个数据集都被划分成70%的训练集和30%的测试集。每个粒子都代表一个特征子集。训练集中被选择的特征子集是通过十折交叉、五近邻(5-NN)的方法来评价分类性能。并在算法的最后,对在训练集中得到Archive 中的粒子集合利用测试集进行评价。
算法的具体参数如下,局部搜索中提出的α=0.02,种群的大小P=30,最大迭代次数为100,Archive的大小为30。本文提出的方法HMIPSO、CMDPSO和MOPSO 算法的公共参数设置相同:学习因子c1和c2取区间[1.5,2.0]的随机值,惯性权重ω取区间[0.1,0.5]的随机值,粒子最大速度vmax=0.6,最小速度vmin=-0.6,阈值Threshold=0.6。在NSGA-II 和BMOABC算法中,采用的是二进制编码,每个粒子是由n个二进制串组成,n为粒子的维度,每位的值为0 表示特征没有被选择,值为1 表示特征被选择。NSGA-II 算法中的突变概率为1/n,交叉概率0.9。BMOABC 算法中,限制参数limit=100,参数T=10 000。对于每个数据集都被独立运行40 次。
4.2 实验结果分析
对于每个数据集,由于要独立运行40 次,故将每次运行得到的外部文档联合成一个并集。在这个并集中,对于有相同特征个数的特征子集,计算它们的平均分类错误率。除此之外,并集中的所有非支配解称之为最优解,并计算最优解的分类错误率。
首先HMIPSO 与MOPSO、CMDPSO 进行比较,证明HMIPSO 通过结合互信息的方法提升了PSO 算法的性能。图5 是其最终的并集在测试集上的比较。而 图6 是HMIPSO 和NSGA-II、BMOABC 算 法在测试集上的比较。在这些图中,“-A”表示40 次独立运行获得的平均分类性能,“-B”表示40 次独立运行获得的最优解的分类性能。其中X轴表示粒子选择的特征个数,Y轴表示分类错误率,图的正上方表示数据集名称以及特征维度和未进行特征选择的分类错误率。
4.2.1 HMIPSO 对分类的影响
图5 和图6 正上方信息为不同数据集使用全部可使用的特征进行评估的分类错误率以及对应的特征个数。数据集Musk1 的特征维度为166,用这166个特征进行分类所得的分类错误率为16.823%。利用本文提出的HMIPSO 算法进行特征选择所得最优解Pareto 面(图中“-B”表示),最大的分类错误率为28.67%,特征个数为12;最小分类错误率为13.14%,特征个数为27。可以看出虽然使用HMIPSO 算法获得的最小特征个数对应的分类错误率要大于未进行特征选择进行分类的错误率,但是最优解中获得的最大特征个数对应的错误率比未进行特征选择进行分类的错误率降低了3.783%,同时特征个数也减少了139 个。
而数据集Wine 特征维度为13,用这13 个特征进行分类所得的分类错误率为30.883%。利用本文提出的HMIPSO 算法进行特征选择所得最优解中,最大的分类错误率为9.33%,降低了21.553%,特征个数为1,减少了12 个特征个数;最小分类错误率为1.67%,降低了29.213%,特征个数为4,降低了9 个特征个数。可看出数据集Wine 使用HMIPSO 进行分类比直接使用全部特征进行分类特征个数不仅减少了,同时分类错误率也降低了。
根据以上分析可得,利用HMIPSO 算法进行分类相对于直接使用所有特征进行分类,能够有效降低分类错误率,同时能很大程度上减少特征个数。
4.2.2 HMIPSO、CMDPSO和MOPSO之间的比较
从图5 可以看出本文提出的混合互信息与粒子群算法的HMIPSO 方法的最优解Pareto 面(图中“-B”表示)大部分都是优于MOPSO 和CMDPSO 方法。并且随着特征的维度增加,HMIPSO 效果则表现越明显。例如,从图5 中可看出在某些维度较小的数据集上,HMIPSO 效果优势并不十分明显。例如维度为24 的数据集German,利用MOPSO 算法得到的解分类错误率为21.67%,特征个数为1;利用CMDPSO 算法得到的最大特征分类错误率为23.00%,特征个数为2,最小分类错误率为22.67%,特征个数为5;利用HMIPSO 算法得到的German 特征数为2 和特征数为4 的时候对应的错误率分别为25.67%和21.00%。通过数据集German 的实验结果可知,虽然HMIPSO 算法最大特征个数比MOPSO算法所获得的特征个数要大,但是分类错误率降低了0.67%;相比较CMDPSO算法,虽然最小分类错误率要大于CMDPSO 算法的最小分类错误率,但是特征个数要少于CMDPSO 算法,同时CMDPSO 算法中特征个数为5 时,其分类错误率为22.67%,比HMIPSO 算法中特征个数为4,分类错误率为21.00%高了1.67%。因此HMIPSO 算法所获得的帕累托面虽然不是完全优于另两种算法,但是在一定程度上也提升了解的质量。
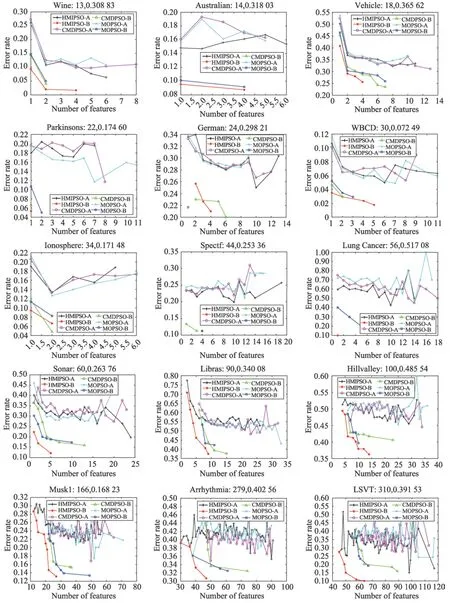
Fig.5 Experimental results of HMIPSO,CMDPSO and MOPSO on test set图5 HMIPSO、CMDPSO 和MOPSO 在测试集上的实验结果
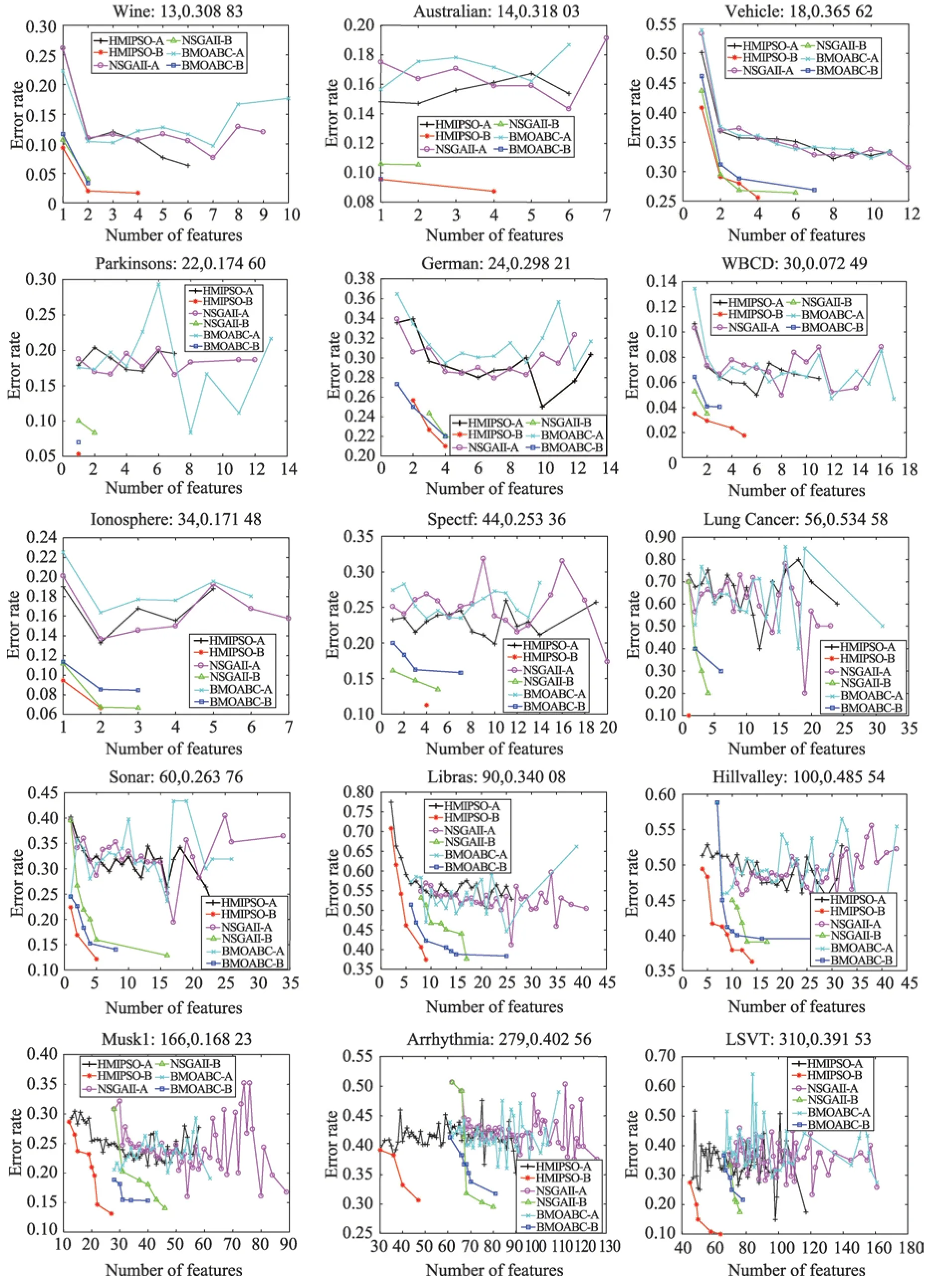
Fig.6 Experimental results of HMIPSO,NSGA-II and BMOABC on test set图6 HMIPSO,NSGA-II和BMOABC 在测试集上的实验结果
除此之外,HMIPSO 在大部分维度较低的数据集上仍能够得到优于其他算法的结果。在保证特征数目不增加的基础上,仍能够降低相应的分类错误率。比如数据集Vehicle,3 个算法均得到了特征为1、2 和4 的3 个结果,但MOPSO 和CMDPSO 算法在特征数为1、2和4时分类错误率分别为46.48%、30.31%、29.43%和45.32%、31.92%、28.75%,而HMIPSO 得到的分类错误率为40.82%、29.09%、25.58%,明显降低了分类错误率。
随着数据集维度的增加,HMIPSO 在降低分类错误率的同时,特征个数也明显减少,获得的最优解Pareto 面要优于另两种算法所获得Pareto 面。具体分析为:对于维度为90 的数据集Libras,其中HMIPSO算法获得最小分类错误率为37.45%,对应的最大特征个数为9。相比较MOPSO 算法的最小分类错误率为42.27%,最大特征个数为11,分类错误率降低了4.82%,同时特征个数减少了两个;相比较CMDPSO算法最小分类错误率为37.64%,最大特征个数为15,分类错误率降低了0.19%的同时,特征个数减少了6个。对于维度为279的数据集Arrhythmia,HMIPSO算法在特征个数为47 时获得最小分类错误率30.66%,MOPSO 算法获得最小分类错误率为32.47%,特征个数为61,CMDPSO算法获得最小分类错误率为32.42%,特征个数为74。HMIPSO 算法相对于MOPSO 算法在降低1.81%错误率的前提下,还使得特征个数减少了14,而相对于CMDPSO 算法在降低1.76%错误率的前提下,特征个数减少了27。
由以上分析,证明基于互信息的局部搜索策略,能够有效减少第一非支配面中粒子的冗余和不相关特征,同时加入了相关特征。在大部分维度较低的数据集上,特征数目相同的情况下,通过局部搜索策略能有效提高算法的分类性能。在高维数据集上表现更为明显。HMIPSO 算法通过局部搜索策略能够搜索到更好的解,对第一非支配面进一步优化,提升特征选择方法的整体性能。
4.2.3 HMIPSO、NSGA-II和BMOABC之间的比较
如图6 可以看出,HMIPSO 算法的最优解(图中“-B”表示),在数据集Vehicle 上虽然在特征数为3的时候分类错误率要高于NSGA-II 算法,但要低于BMOABC 算法。3 个算法都获得了特征数为1 和2的两个解,而对应的HMIPSO 算法的分类错误率40.82%、29.09%都比另两种算法要低。BMOABC 在特征个数为7 和NSGA-II算法在特征数为6 的时候分别获得最小分类错误率26.86%和26.38%,而HMIPSO在特征数为4 的时候获得最低分类错误率25.58%,特征个数和分类错误率都优于另两种算法。故可以看出HMIPSO 算法在数据集Vehicle 上优于BMOABC算法,但是并不完全优于NSGA-II算法。相似的结果还有数据集German,从图6 中可以看出,HMIPSO 算法在数据集German 上获得Pareto 面优于NSGA-II 所获得的Pareto 面;与MOABC 算法相比,HMIPSO 除了特征个数为2 时分类错误率高于MOABC,其他两个解都优于MOABC。而对于其他的低维的数据集,明显能看出HMIPSO 算法优化了Pareto 面。
对于较高维数据集,在降低错误率的同时,减少了冗余特征,大大降低了特征子集的维度。例如,在维度为60 的Sonar数据集上,HMIPSO 获得3 个解,特征数为1 的时候,错误率为22.38%,特征数为2 的时候,错误率为16.90%,特征数为5 的时候,错误率为12.14%。NSGA-II算法在特征数为1的时候错误率为39.52%,比HMIPSO 高了17.14%;特征数为2时,错误率为26.67%,比HMIPSO 高了9.77%;特征数为5 时,错误率为15.59%,比HMIPSO 高了3.45%。BMOABC算法在特征数1 时错误率为24.52%,比HMIPSO 高了2.14%;在特征数为2 时错误率为22.62%,比HMIPSO高了5.72%。虽然BMOABC 算法没有获得一个特征个数为5 的解,但是其获得的最大特征个数8 所对应的最小分类错误率为14.05%,比HMIPSO 算法中特征数为5 所对应的最小分类错误率都高。对于维度为100 的数据集Hillvalley,HMIPSO 算法获得解最大特征个数为14,对应的最小分类错误率为36.29%。而NSGA-II 算法获得解最大特征个数为17,对应的最小分类错误率为39.06%。BMOABC 算法获得解最大特征个数为36,对应的最小分类错误率为39.53%。HMIPSO 算法相对于NSGA-II 算法在数据集Hillvalley 所获得的解的最大特征个数降低了3,而相对于BMOABC 算法最大特征个数降低了22。同时HMIPSO 获得最小分类错误率比NSGA-II 降低了2.77%,比BMOABC 降低了3.24%。
再比较维度更大的数据集LSVT,HMIPSO 算法获得解最大特征个数为64,对应的最小分类错误率为10.00%。NSGA-II算法获得解最大特征个数为76,对应的最小分类错误率为17.50%,获得的最小特征个数为70,对应的最大错误率为33.33%。BMOABC 算法获得解的最大特征个数为78,对应的最小分类错误率为21.67%,获得的最小特征个数为66,对应的最大错误率为36.67%。可以看出,在数据集LSVT 上,HIMPSO 不仅获得的最大特征数要少于另两种算法获得的解集中的任何解的特征数,而且对应的分类错误率低于另两种算法获得任意一个解。通过以上具体分析,充分验证了HMIPSO 算法能够得到比NSGA-II和BMOABC 算法更好的Pareto 面。
5 结束语
本文利用一个自适应突变操作来扰动种群,避免PSO 算法在进行全局搜索时快速收敛但容易陷入局部最优的问题,以及利用互信息方法能够表示数据本身之间依赖程度的优点,对种群每次迭代产生的Pareto 前沿面进行局部搜索,提出了混合互信息和粒子群算法的多目标特征选择的方法(HMIPSO)。HMIPSO 能有效地使粒子增加相关特征或删除不相关和冗余特征,很好地对粒子起到探索作用,平衡了粒子的全局搜索和局部搜索。通过在15 个数据集上进行比较,不仅能提高粒子群算法在多目标特征选择问题上的性能,也优于另外提出的两个算法。
