无逆矩阵在线序列极限学习机*

左鹏玉，王士同

江南大学 数字媒体学院，江苏 无锡214122

1 引言

近年来，神经网络已经得到广泛研究，并且成功应用到现实问题中[1-6]。传统的单隐层前馈神经网络（single hidden-layer feedforward neural network,SLFN）中，所有的参数都需要调整，不同层的参数之间存在着依赖性，训练效率低，学习速度慢。为此，Huang 等人提出了极限学习机（extreme learning machine,ELM），该算法无需调整任何参数，只需要随机产生输入权重及偏差，直接通过隐含层输出矩阵的广义逆矩阵计算得出输出权重[7]。相比于传统的SLFN，ELM 在保证了算法学习性能的基础上，对速度有了明显提升[8]。但由于ELM 无需调整任何参数，网络结构在训练过程中固定不变，而其中隐含层的节点数对训练效果具有决定性影响，因此便产生了最优隐含层节点数的问题。

为了解决最优隐含层节点数的问题，Li 等人提出了无逆矩阵极限学习机（inverse-free extreme learning machine,IF-ELM）的增量学习算法，该算法通过逐步增加隐含层节点数来更新隐含层的输出权重，通过不断调整隐含层节点数使得训练模型的性能达到最优[9]。文献[9]用大量实验证明了在隐含层参数相同的情况下，IF-ELM 算法与经典ELM 算法学习性能是一致的。经典ELM 在最小二乘方法下，训练误差具有最优性，这就意味着IF-ELM 的节点增加策略也具有最优性。此算法是批量学习算法，需一次性获得所有的训练样本进行学习。当收到新的数据时，批量学习方法需要将过去的数据和新的数据一起进行训练。算法在涉及到训练数据的迭代时，没有进一步考虑在线学习情况下的应用，从而浪费了大量的时间。

学习是一个持续的过程，在许多实际应用中，训练数据集并不能一次性获得。当一些新的数据加入到训练模型时，批量学习必须重复使用过去的数据进行学习，因此需要更多时间，效率较低。在线学习算法不同于批量学习算法，在接收到新数据时不需要重复计算已经训练过的数据，不仅减少了时间和空间的需求，且更好地满足了实际应用。

Huang 等人提出了在线序列极限学习机（online sequential extreme learning machine,OS-ELM），可以逐个或多个地增添学习数据，减少了训练数据的迭代过程，从而节省了大量的学习时间[10]。文献[11]提出了具有遗忘系数的极限学习机（forgetting parameters extreme learning machine,FP-ELM），该算法注重当前数据，在OS-ELM 的基础上为旧数据块添加遗忘系数。文献[12]提出了在线序列λ1 正则化极限学习机（online sequential λ1-regularized-ELM,OS-λ1-ELM），通过增加惩罚项的方式有效避免了过拟合问题，提高了模型的泛化能力。虽然以上这些学习算法已经具备了在线学习的能力，但是在最初确定隐含层节点数时涉及到了逆运算，导致了大量的计算开销。因此，如何高效求解这些在线学习算法的最佳隐含层节点数就变得十分迫切。

本文在IF-ELM 算法基础上引入了在线学习的思想，提出无逆矩阵在线序列极限学习机（inversematrix-free online sequential extreme learning machine,IOS-ELM）算法，计算出合适的隐含层节点数后再加入新增数据，增强了算法的实时学习能力。该算法不仅可以逐步将数据加入模型训练，还可以丢弃已经完成训练的数据。当新的单个或多个数据加入到训练模型时，在线学习算法只需要学习新的数据，而无需再次学习过去已经分析过的数据。所提的IOSELM 算法源于批量学习的IF-ELM 算法，且IF-ELM算法的性能已经在回归和分类问题上得到了验证[9]。由实验部分可知，当不断增加训练样本时，本文所提的IOS-ELM 算法的学习在保证性能不变的情况下，速度明显快于无逆矩阵极限学习机。

2 无逆矩阵极限学习机

2.1 极限学习机

ELM 是在SLFN 的基础上提出的一种学习效率高且泛化性能好的学习方法。不同于传统的神经网络求解权重的方法，ELM 只需随机选取输入层和隐含层的连接权重和偏差，通过隐含层输出矩阵的伪逆运算，分析计算出隐含层和输出层的连接权重。同时，ELM 的逼近原理表明：在一定条件下，使用任意给定输入权重的ELM 算法，能以任意小误差逼近任何非线性连续函数。

对于n个输入层节点，l个隐含层节点和m个输出层节点，ELM 的表达式如下：

其中，fj为第j个输出节点的值，g(ai,bi,xj)是与输入数据xj相对应的第i个隐含层节点的值。g(⋅)是一个激活函数，如sigmoid等。wi是输入层到第i个隐含层节点的连接权重，bi是第i个隐含层节点的偏差值，βi是第i个隐含层节点到输出层的连接权重。

2.2 无逆矩阵极限学习机

实际情况下，计算量与隐含层节点数成正比，训练时间随着隐含层节点数的增多而加长。为缩短训练时间，实验应尽量减少隐含层节点数。但只有在隐含层节点数接近无穷大时，ELM 才能以任意小的误差逼近任何非线性连续函数，达到最优精度。为了使学习效率达到较优的状态，需要协调以上两个因素。在机器学习中，逐步增加隐含层节点数是使训练达到所需精度的一种常用方法。IF-ELM 算法便使用隐含层节点数增加策略，其l+1 个隐含层节点的输出权重可以利用l个隐含层节点的输出权重计算得出，从而减少了计算量。

由xi和yi分别表示第i个训练输入和相应的第i个训练输出。给定训练集{(x1,y1)…(xi,yi)…(xk,yk)}，输入权重W和偏差b，ELM 的训练误差则取决于其输出权重。对于l个隐层节点的ELM，它的输出权重为：

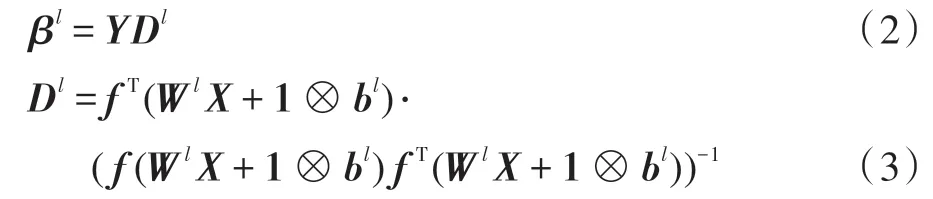
其中，H=f(WlX+1 ⊗bl)，故：

记Y=[y1,y2,…,yk]∈Rm×k。只有当HHT是非奇异时，式（4）才能成立。此处使用了Tikhonov正则化方法来满足这些约束条件，以避免出现过拟合现象[13-14]。其中I为单位矩阵：

对于具有l+1 个隐含层节点的ELM，其隐含层的输入权重Wl+1和偏差bl+1如下：

其中，Wl和bl是l个隐含层节点对应的输入权重和偏差值，w∈Rn所取数值与Wl中的数据元素具有相同的概率分布，bl+1∈R 所取数值与bl中的数据元素具有相同的概率分布。

l+1 个隐含层节点的ELM 的输出权重可由l个隐含层节点的输出权重求出，为：

由式（3）和式（5）可得：

设d=f(XTw+bl+11)，式（8）可写成以下形式：

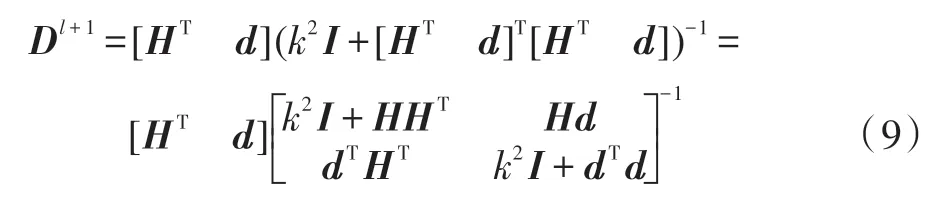
由Schur Complement公式可得：

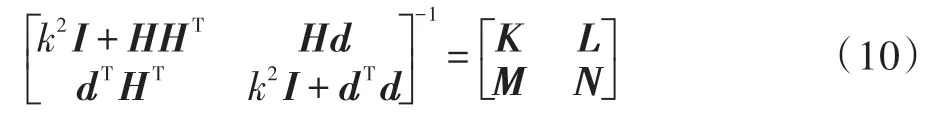
其中：

因此，由式（9）、式（10）可得：

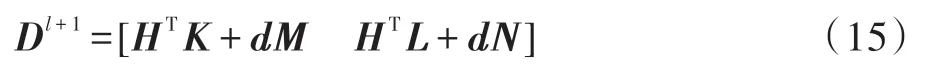
假 设m=k2I+dTd-dTHT(k2I+HHT)-1Hd且m≠0，式（11）可由Sherman-Morrison 公式转化为下式：

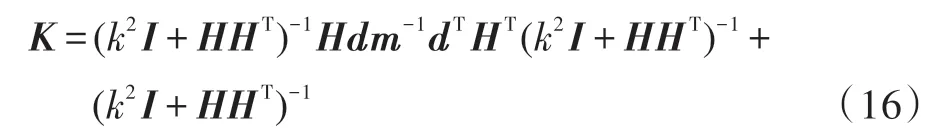
Dl+1的推算公式可将式（11）、式（12）、式（13）和式（14）带入到式（15）中得到。由含有l个隐含层节点的Dl推出Dl+1的过程如下：

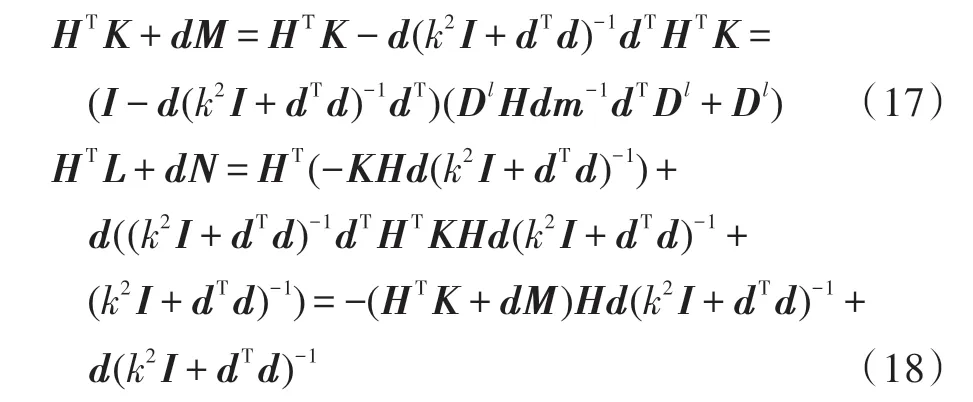
由式（15）、式（17）、式（18）可以得到：

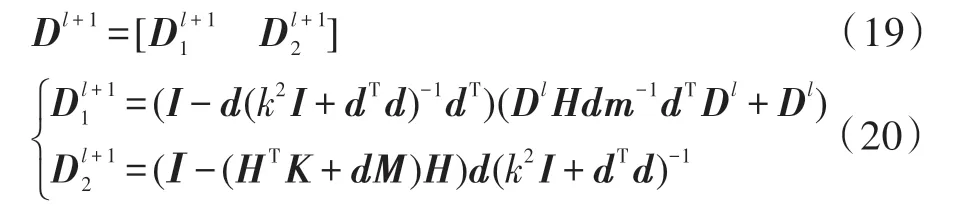
根据以上推导过程不难发现，通过逐步增加隐含节点数量这一方法，可将具有期望近似误差η(η＞0)的Tikhonov正则化ELM 应用到回归问题的求解中。

3 在线序列极限学习机

ELM 对模型更新时需要重新代入所有数据，不能很好地应用在实际场景中。针对这一问题，OSELM 应运而生。在加入新的训练数据后，隐含层的输出矩阵由H变为[H h]，其中h为新增数据隐含层的输出矩阵。由可以推出新的输出层权重的公式，具体如下：

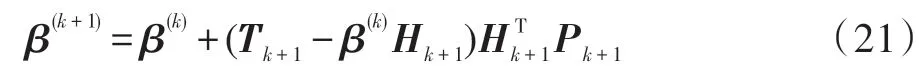
其中，Pk+1计算公式如下：

从OS-ELM 的推算可以得出，当H0的秩等于隐含层节点数时，OS-ELM 和ELM 在训练误差和泛化性能等方面表现相近。OS-ELM 包括初始部分和在线学习两部分。在初始部分，训练算法随机给定隐含层的输入权重和偏差，分析计算隐含层的输出权重。其中，隐含层节点数要小于训练样本数。在初始化阶段之后进入在线学习部分，学习算法根据需要逐步学习新增数据。

4 无逆矩阵在线序列极限学习机

4.1 算法过程

定义：期望的训练误差η，输入维度为n，输出维度为m，训练集的初始数目为k0，增加的训练样本的数目为k1，初始的训练集输入为，训练集输出为。初始的ELM训练模型有l个隐含层节点，输入权重为，隐含层的偏差值为，输出权重为。

步骤1 计算出合适的隐含层节点数目：

步骤1.1 给出初始的训练样本集(xi,yi)，X=[x1,。

步骤1.2 给定初始的隐含层节点数目l0，期望的输出均方误差η。

步骤1.3 任意取值输入权重W和偏差b。

步骤1.4 增加任意数量隐含层节点数la，则l0=l0+la，任意选定增加的隐含层节点的输入权重w和偏差b0，更新输入权重W和偏差b：

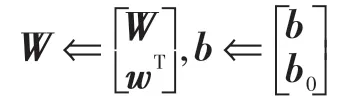
步骤1.5 计算d=f(XTw+b01)的值。

步骤1.6 计算D的值：

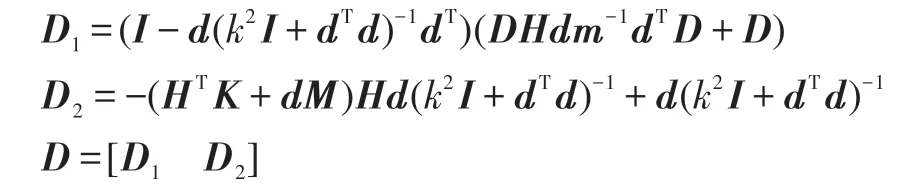
步骤1.7 更新隐含层的输出权重β=YD。

步骤1.8 计算出增加隐含层节点后mse的值，其中mse=MSE(Y-βH),若mse小于期望值则转至步骤2，若mse大于期望值则跳转到步骤1.4。

步骤2 增加训练样本数目：

步骤2.1 假设新增加的一批训练样本的个数为k1，每次增加n个训练样本，计算出隐含层的输出矩阵H。

步骤2.2 计算隐含层的输出权重β(k+1)：

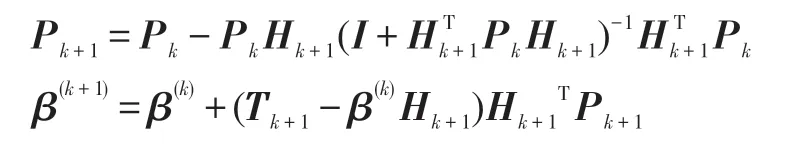
步骤2.3 当增加的训练样本个数大于k1时，则继续步骤2.4；当增加的训练样本小于k1时，则跳转到步骤2.1。

步骤2.4 输出权重β(k+1)。

4.2 算法时间复杂度分析

此节，对IOS-ELM 算法的时间复杂度进行分析。IOS-ELM 算法时间复杂度分析分为两部分，分别对应上述的步骤1 和步骤2。在步骤1 中，由文献[3]可以得到，对于每i次迭代，算法的时间复杂度为ο(k0li)，其中k0为训练样本的个数，li为第i次迭代时隐含层的节点数。在步骤2 中，对于第i次迭代，算法的时间复杂度为ο(kil0)，其中ki表示第i次迭代时训练样本的个数，l0为步骤1 输出的最终的节点数。由上述分析可以看出，所提算法的时间复杂度只与训练样本的数据量和其隐含层节点数有关，一般情况而言，数据集维度的增加对时间复杂度没有影响。但在实际实验时，维数的增加可能需要更多的隐节点。随着新增训练样本数量的增加，对算法的时间复杂度会产生一定的影响。如果增加的样本数远大于原始的样本数，则理论上会增大算法的时间复杂度。例如对于步骤1 中，对于每i次迭代，原始训练样本为k0，增加的样本数为，如果，则此时的时间复杂度由ο(k0li)增加到。不过，实际中因为研究的是在线情形，这种情况并不多见。如果增加的训练样本数没有原始样本数多，则对算法的时间复杂度没有影响。

4.3 算法总结

本文所提的IOS-ELM 算法，对于回归问题在速度和性能都有很好表现。由于回归与分类的内在联系，同样的框架也可以应用于分类问题[15]。对于一个m类分类问题，属于第i类的训练样本的输出可以表示为y=ei，其中ei∈Rm，是一个第i项为1，其他项为0 的向量。可以按照与回归问题相同的步骤来训练IOS-ELM。在预测阶段，IOS-ELM 会根据测试数据生成m维的输出向量，其中最大元素所在位置即为分类标签。例如，若输出向量的m个输出元素中，第i个元素中具有最大值，则样本被分类到第i类中。由以上可知，该算法可较好地适用于回归和分类问题。

5 实验分析

本章进行实验分析，以验证所提出的无逆矩阵在线序列极限学习机算法的有效性。为了更好评估算法的性能，实验使用机器学习领域中具有几个代表性的数据集进行实验。这些数据集分别来自加利福利亚大学Irvine机器学习库[16]和支持向量机数据库[17]，数据集在数据量和维度上有代表性。对于回归问题，实验所用数据集Energy efficiency数据集[18]、Housing 数据集[19]、Parkinson数据集[20]、Airfoil self-noise数据集[21]如表1所示。在测试实验中，对训练数据集进行预处理，所有输入数据和输出数据都归一化到[-1,1]。对于分类问题，所用数据集Diabetes 数据集[16]、Musk 数据集[22]、Feritility数据集[23]、Spambase数据集[16]、CNAE-9 数据集、Multiple Features 数据集如表2 所示。实验结果如表3、表4 所示。

Table 1 Introduction to regression data sets表1 回归数据集介绍

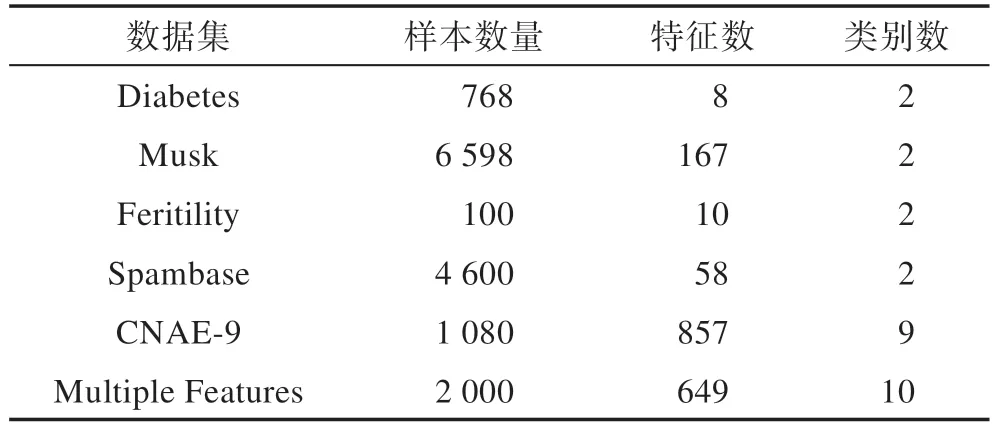
Table 2 Introduction to classification data sets表2 分类实验数据集介绍

5.1 实验环境

本文所有实验均在同一环境下完成，采用在Windows 10 环境下搭建系统，计算机处理器配置为Intel®CoreTMi3-4150 CPU@3.5 GHz，内存4 GB，主算法在Matlab2016b下完成。

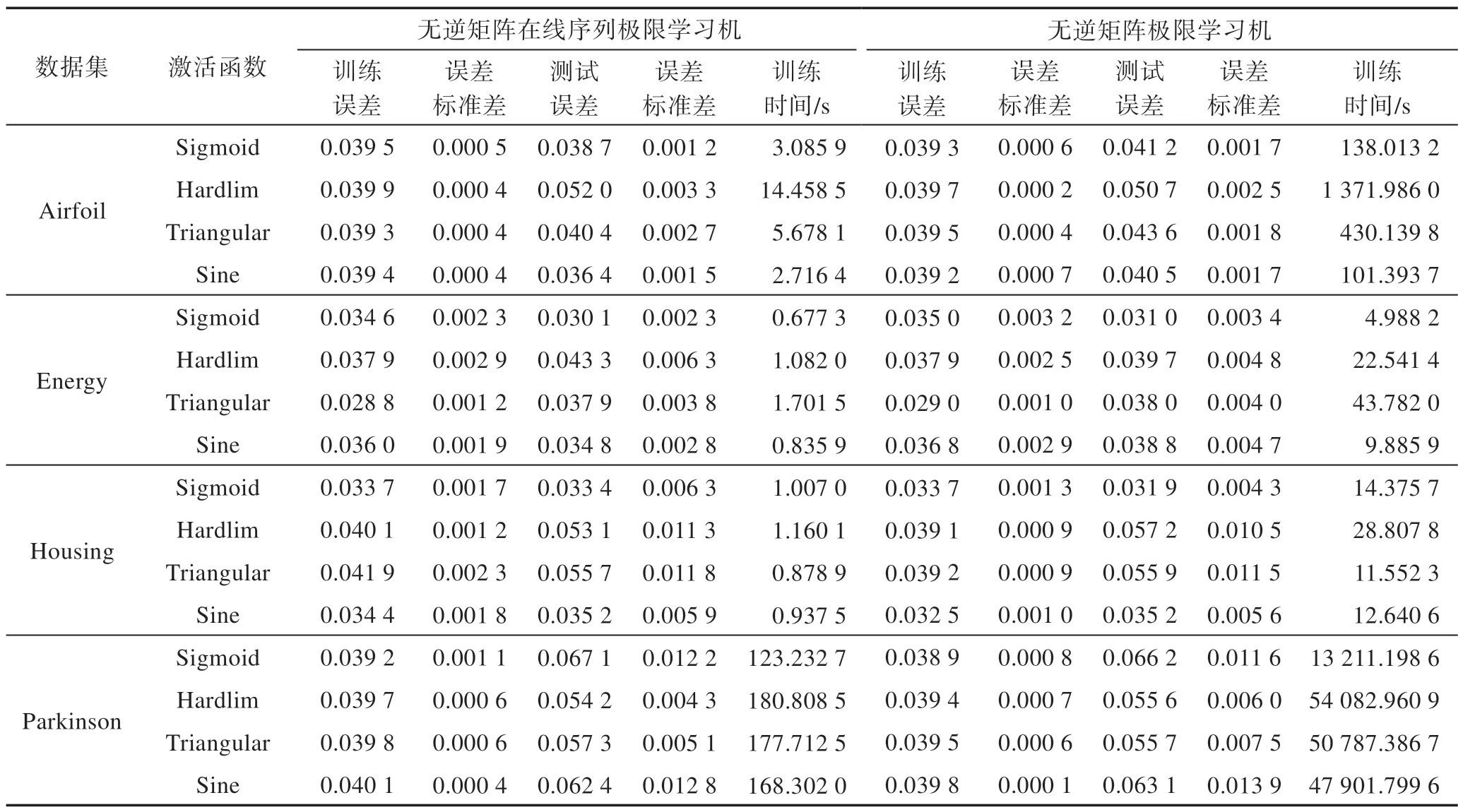
Table 3 Experimental results on regression datasets表3 回归数据集的实验结果

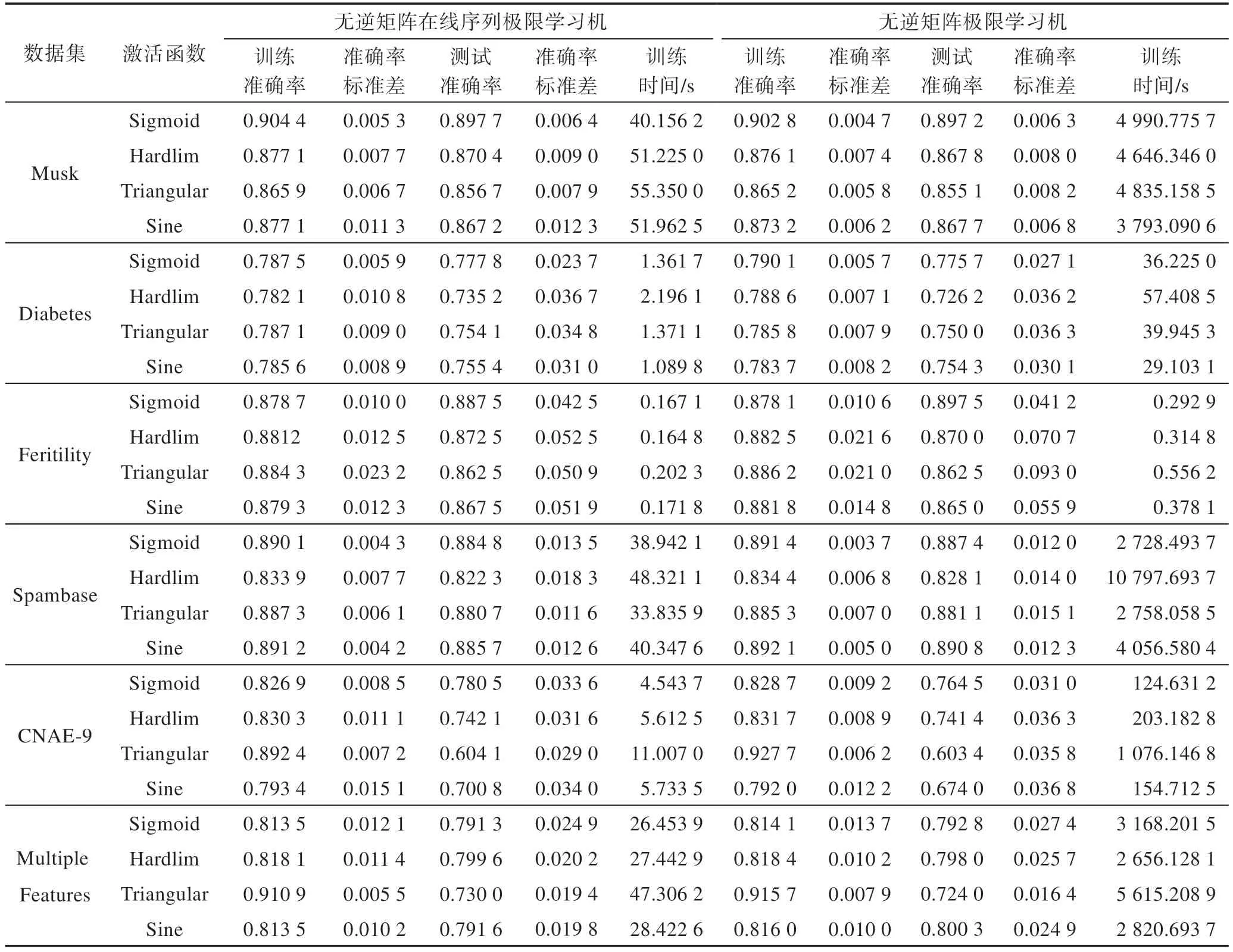
Table 4 Experimental results on classification datasets表4 分类数据集的实验结果

5.2 评估指标

为保证实验结果真实准确，每个数据集对应的各个激活函数都进行20 次实验，然后取其平均值作为最终结果。每次实验随机选取数据集的4/5 作为训练集，其他的作为测试集。且每次选取训练集的9/10 作为初始部分的样本，剩余的1/10 作为在线学习的样本。对于分类问题，采用常见准确率（accuracy）作为衡量指标。对于回归问题，采用均方误差（mse）评估所提出算法的预测性能。并计算分类实验中准确率和回归实验中均方误差的标准差来评估预测的离散程度。

5.3 实验结果

表3 显示了所提出的具有不同激活函数的IOSELM 算法的回归性能，激活函数包括Sigmoid 函数、Triangular 函数、Hardlim 函数和Sine 函数。在实验中使用Tikhonov 正则化算法来避免过拟合。实验部分将所提IOS-ELM 在线学习算法的在线训练时间与传统的IF-ELM 批量学习算法学习时间的结果进行比较。由表3 中的结果可以得出，两个算法在不断增加训练样本之后，所提的IOS-ELM 算法在保证了与IFELM 算法相近的学习性能的情况下，学习速度有了明显的提高，且新增的样本数量越大，所节省的时间也越多。

表4 显示了所提的IOS-ELM 算法与IF-ELM 算法在不同激活函数情况下的分类性能的比较。实验所用激活函数与测试回归性能所用激活函数相同。由表4 可以看出所提的IOS-ELM 算法与IF-ELM 算法的分类准确率相近（两个算法的分类的测试准确率相差不超过0.5%），但所提算法在速度上确实有较大的提升。其中CNAE-9 数据集与Diabetes 数据集的数据量相差不大，但是所提IOS-ELM 算法的实验中，CNAE-9 数据集的训练时间是Diabetes 数据集的4 倍左右。这是因为前者数据集的维度和类别数都较大，为达到所需精度选取的隐含层节点数较多。最终，训练时间也随着隐含层节点数的增多而增大。

6 结束语

针对无逆矩阵极限学习机只能将所有数据一次性输入给训练模型这一问题，本文提出了一个快速准确的无逆矩阵在线序列极限学习机算法。该算法源于批量学习的无逆矩阵极限学习机算法，理论上在一定条件下能够以任意小期望误差逼近任意非线性连续函数。其首先利用初次的输入样本集找到合适的隐含层节点，然后可以将单个或多个样本数据逐步进入到训练模型当中，只要确定所期望的输出误差，所有隐含层参数都是任意给定。实验结果证明，该算法与无逆矩阵极限学习机有着相同的精度和泛化能力，在速度上有很大的提升。在未来的进一步发展中可以在增加样本数据的同时再增加或删减隐含层节点，以达到更好的学习效果。