面向并行的动态增量式Delaunay 三角剖分算法*
2020-01-11杨昊禹
杨昊禹,刘 利,张 诚,于 灏
清华大学 地球系统科学系 地球系统数值模拟教育部重点实验室,北京100084
1 引言
三角剖分[1]是计算几何学领域中基础而又重要的研究内容,其可以将平面或球面等区域中的散点转化为以这些散点为顶点的三角形网格。三角剖分技术可应用于众多领域,例如逆向工程、计算机可视化、地理信息系统、有限元分析、地球系统模式等。作为一个基础算法,三角剖分的计算效率可直接影响到上层应用的整体效率,如何快速高效地完成三角剖分一直是业界重要的讨论话题[2-4]。
三角剖分算法相关研究已经有较久远的历史。如今最常讨论的Delaunay 三角剖分由Boris Delaunay最先提出。Delaunay 三角剖分要求每个三角形均满足空圆特性,即任意一个三角形的外接圆内均不包含任何其他点。
目前二维平面Delaunay 三角剖分算法(简称为三角剖分算法)可分为多种不同类型,包括插入法、构造法、分治法、高维镶嵌法等,其中最常用的算法为插入法和分治法。插入法逻辑简单、易于实现,分治法通常拥有最低的时间复杂度,可达到O(nlgn),其中n表示点数。这两种算法讨论详见第2 章。
地球系统模式是气候演变规律研究、未来气候预测和无缝隙数值预报所不可或缺的科学工具,由分别模拟大气、陆面、海洋和海冰等地球系统圈层的分量模式通过耦合器耦合而成[5-7]。由于不同分量模式所使用的网格可能不同,因此需要使用插值技术来实现耦合变量在不同网格间的插值。插值技术的实现依赖于临近点搜索技术,而三角剖分的实现正好可以给临近点搜索提供具有通用性的基础支持。
虽然三角剖分算法已具有较低时间复杂度,但随着网格分辨率的不断提高,三角剖分的开销仍会越来越大,这样的开销仍不可忽略。为了寻求进一步的加速,大家开始关注并行三角剖分的研究。
并行三角剖分算法按照并行分块策略的不同,可以分为非重叠分块法和重叠式分块法两类。非重叠分块法将全球分为若干互不重叠的子块,并行地对各块进行局地三角剖分,最后通过串行缝合操作将各子块合并为最终结果。重叠式分块法会在分块时保持各子块间的部分重叠,避免了合并时的串行缝合操作。虽然重叠会引入少量额外计算,但因其可以避免串行缝合,因此具有更高的并行可扩展性。在并行规模越来越大的今天,重叠式分块法比非重叠分块法有更大优势。
重叠式分块法现在也可分为两个子类,静态重叠法[8]和动态重叠法[9]。静态重叠法在分块之时就已经确定下各分块的大小及互相重叠的程度。动态重叠法则允许算法在执行中动态改变分块重叠区的大小。因为重叠区域过小会造成子块间的公共三角形不一致,最终导致并行计算结果有误(串行与并行计算结果不同),所以静态重叠法往往使用过饱和的重叠区域以保证结果正确,但这样会引入过多额外计算开销,拖慢整体速度。动态重叠法因为支持分块重叠区的变动,所以可以降低上述额外开销,并使最终结果的正确性更可靠。
动态重叠法带来了一个新的问题,对于单一分块的局地三角剖分,在完成对已有点的三角剖分后,若重叠区扩大,增加了若干新的点,如何求取考虑了新增点的三角剖分结果?一般说来,有两种实现方式:第一种方式是删除已有三角剖分结果后,重新求解所有点(包含新增点)的三角剖分结果;第二种方式是在保留已有三角剖分结果基础上,增量求解新增点对三角剖分结果的调整。毫无疑问,后者将比前者更佳高效,本文将后者称为增量三角剖分算法。基于动态重叠法设计的并行三角化软件PatCC1[9](parallel triangulation algorithm with commonality and parallel consistency,version 1)在实现增量三角剖分时采用了上述第一种方式,若能设计出第二种方式的增量实现,则会给PatCC1 带来更高的性能提升。
当前已有的三角剖分算法都无法完全满足增量三角剖分需求,为此本文提出了TID(truly incremental Delaunay)算法,该算法可以高效实现增量三角剖分。
2 相关工作
2.1 插入法
插入法是最为常用的三角剖分算法。该类算法首先创建一个假想的极大三角形以包围住所有点,随后逐步插入这些点,并对每个点进行如下操作:定位该点所在的三角形,将该三角形替换为3 个或两个子三角形(后称分裂操作),然后判断相应边的Delaunay 合法性并进行适当的翻转操作[10](又称局部优化)。待所有点插入完成,最终三角剖分结果也随之完成。
插入法的关键步骤即为点的定位,即判断一个点被当前哪个三角形所包含。现有定位方式可分为以下四类:Walking 方法[11]、Delaunay 树方法[12]、索引矩阵法[13]以及分解定位法[14-15]。本文称使用前三类定位方式的插入法为在线插入法,使用分解定位法的插入法为离线插入法。
Walking 方法的核心操作即为在当前边的临近边中选取离插入点最近的边作为新的当前边,该方法从随机某边开始,重复执行上述操作来逐步逼近插入点所在的三角形。Delaunay 树方法,会在插点过程中以三角形为节点建立一个搜索树,点的定位即可通过遍历搜索树来完成。索引矩阵法,将整个区域分为若干矩形子域,用以粗略记录三角形的位置信息。该方法中点的定位均通过初步定位、局地精确遍历两个步骤来完成。在分解定位法中,一个三角形除包含三个顶点外,还包含若干位于该三角形中的尚未插入的点(称为待插点)。在生成若干新三角形后,待插点会被分配到这些三角形中。
Walking 方法中临边快速选取的实现方法及数据结构较为复杂;Delaunay 方法的缺点是内存占用大,维护三角形间的树形关系较为困难;索引矩阵法的缺点则是索引效率受总点数及矩阵大小的影响,输入点规模的变化给定位效率带来的波动较大。此外,以上三种定位方法的逐点定位方法无法高效利用中央处理器(central processing unit,CPU)高速缓存(cache)带来的加速效果。分解定位法对点进行统一管理,更易通过连续访存实现定位,具有较高的计算效率,但因其为离线算法,必须事先准备好所有点。
2.2 分治法
分治法三角剖分主要由划分与合并两部分操作组成。划分即为按照一定的方法将平面或球面的一个区域分解为若干子区域,然后分别为各子区域单独求解三角剖分;合并则是将各子区域的三角剖分结果整合为一个整体,这过程的局部优化操作会给三角剖分的结果带来调整。常见的划分方法主要包括一维二分法(沿水平线或垂线二分)和二维二分法(沿水平线和垂线交替二分)。
一方面,当区域中的点很少时,分治法的效率会远低于插入法;另一方面,分治法合并过程实现起来比较困难,特别是当需要保证Delaunay 三角剖分的空圆特性时。
3 增量算法设计
增量三角剖分的需求来源于动态重叠式并行三角剖分算法,该类并行算法分块范围的动态变化需要在已有三角剖分的基础上加入新增点,并求解更新后的三角剖分。可以总结出该增量三角剖分场景具有以下特点:
(1)新增点大多位于已有三角形外,少量位于已有三角形内(后文分别称为外增点和内增点)。
(2)性能需求:新增点并非逐一加入,而是批量式加入。
(3)现有的动态重叠法并行算法PatCC1 使用了分解定位插入法来完成局地三角化。
对于增量三角化的实现,在线插入法可以支持内增点,但无法高效支持外增点。虽然可以采取折中策略避免出现外增点,即设置一个非常大的初始三角形,但却会带来较大性能损失。例如,极大初始三角形会导致索引矩阵覆盖范围很大,但常用的却只为中间少量索引块;极大初始三角形也会使Delaunay 树不平衡,增加树深,增加单次搜索的耗时。
离线插入法虽然支持内增点,但每次增加点均需要通过全局搜索对点进行定位,效率低下,此外离线插入法也无法支持外增点。
分治法既不支持内增点,也不支持外增点。这是因为分治法不是逐点插入型算法,同时分治法的合并操作缺乏通用性,无法实现对已有区块和新增区块在任意位置下的合并。
综上所述,无法基于分治法而只能基于插入法来实现增量三角剖分。由于分解定位插入法具有很好的数据访问局部性,且PatCC1 也采用该算法来实现局地三角剖分,因此基于分解定位插入法来实现增量三角剖分,既有利于取得高效率,也有利于重用PatCC1 中分解定位插入法的实现,但必须解决以下两个问题:
(1)外增点的支持;
(2)高效实现所有新增点到三角形的定位。
为此,本文引入原有剖分的扩展操作来将所有外增点均转化为内增点,并使用索引技术实现新增点的高效定位,设计出了增量三角剖分算法TID。
3.1 相关名词
假想矩形:算法为了便于执行插入法三角剖分所引入包含所有点的矩形。
假想点:假想矩形的4 个顶点。
原有点:在增加新点之前已有的点。
新增点:需要被插入到原有剖分中的点。
原有剖分:在增加新点之前已有的三角剖分。
外扩剖分:原有剖分经过扩展后得到的新剖分。
外层三角形:顶点中包含假想点的三角形。
三角形的外边框:能包围住该三角形,且各边均垂直或平行于坐标轴横轴的最小矩形。
3.2 整体设计
增量算法整体流程如图1,主要由以下步骤组成:
(1)初始状态的设定,主要涉及假想点的生成。
(2)判断是否存在新增点,若存在,则执行下一步,否则算法结束。
(3)根据新增点对原有剖分进行适当外扩。
(4)定位新增点至原有剖分中。
(5)基于原有三角剖分及新增点,动态更新三角剖分,返回(2)。

Fig.1 Main flowchart of TID图1 TID 算法流程图
该算法可以满足前述两点需求,其中(3)实现了外增点的支持,(4)可以完成新增点的高效定位。
3.3 算法实现
本节将详细讨论TID 算法各步骤的具体实现以及算法对四点共圆情况的特殊处理。
3.3.1 初始化阶段
与其他插入法类似,TID 算法使用假想矩形包围住所有点。在初始化阶段,算法根据第一轮新增点的位置分布来创建假想矩形,保证假想矩形能够包围住所有第一轮新增点。
3.3.2 原有剖分外扩
若原有剖分对应的假想矩形不能包含全部已有新增点,则算法会首先扩大该假想矩形,然后更新所有外层三角形的顶点坐标,从而完成原有剖分外扩。
为确定假想矩形的扩大范围,算法先扫描新增点并确定坐标的边界,然后分别以边界边长的预定比例对边界最小值进行减小,对最大值进行增加,进而得到预期外扩范围。本文将上述预定比例称为外扩参数,与该参数相关的测试结果及讨论见4.4 节。
原有剖分外扩过程如图2,图中的5 个实心圆点为原有点,4 个空心圆点为假想点,3 个空心菱形为新增点,图2(a)和图2(b)分别代表扩展前后三角剖分的状态。通过原有剖分的外扩,所有外增点均已被转化为内增点。在外扩后,外层三角形由于形状的变化,其Delaunay 合法性可能会受到改变,但因为这些外层三角形仅为假想三角形,所以不会对最终结果产生影响。

Fig.2 Expansion of existing triangulation图2 原有剖分外扩示意图
3.3.3 新增点定位
新增点定位即将各新增点根据位置关系定位到外扩剖分的某个三角形中。TID 算法通过索引矩阵法来完成高效定位。
算法首先把当前外扩剖分覆盖范围均匀划分为若干索引块并建立索引矩阵,再把各新增点放入相应索引块内(将含有新增点的索引块标记为非空索引块);然后扫描外扩剖分中的所有三角形,若三角形与非空索引块的区域有重叠,则将其记录在相应索引块中;最后依次在各非空索引块内,确定新增点所在的三角形,从而实现新增点的快速定位。
索引块的数量是影响新增点定位效率的重要参数。索引块过少会导致一个索引块包含有很多新增点和三角形,从而导致索引效率的降低;索引块过多虽然会降低复杂度,但会导致Cachemiss 增多,无法较好利用CPU 高速缓存。因此,应该在保证索引过程不增加TID 算法复杂度的前提下,选择最小的索引块数量。对于不同的数据规模,TID 算法会根据公式动态推测索引块的最优数量。该公式的推导详见3.3.6 小节,相关测试结果详见4.3 节。当已有三角形数量很少时,使用索引定位法的意义不大,此时将直接使用全局搜索。
为了加快点与三角形位置关系的判断,TID 算法会先使用三角形的外边框进行预判,只有当点位于外边框内时,才会精确判断该点是否位于三角形内。
3.3.4 三角剖分动态更新
在经过新增点定位后,所有新增点均已被成组地分配到若干三角形中,称这些三角形为非空三角形。TID 算法通过单独对每一个非空三角形执行分裂操作来完成整体三角剖分的更新。分裂操作由以下三步完成:
(1)子三角形的生成;
(2)局部优化;
(3)父三角形待插点到子三角形的分配。
首先,TID 算法从父三角形待插点中取出离父三角形重心最近的点,以该点作为插入点,连接该点与父三角形各顶点形成多个子三角形。如图3 所示,当插入点位于父三角形内时,会形成3 个子三角形;当插入点位于父三角形某一边上时,则在形成两个子三角形同时,将共享该边的另一个三角形也分裂为两个子三角形,共生成4 个子三角形。
其次,对所有新生成的子三角形进行局部优化。即判断所有子三角形边的Delaunay 合法性,若不合法则通过翻转操作将其转化为合法边。翻转操作会引入新的父三角形和子三角形。
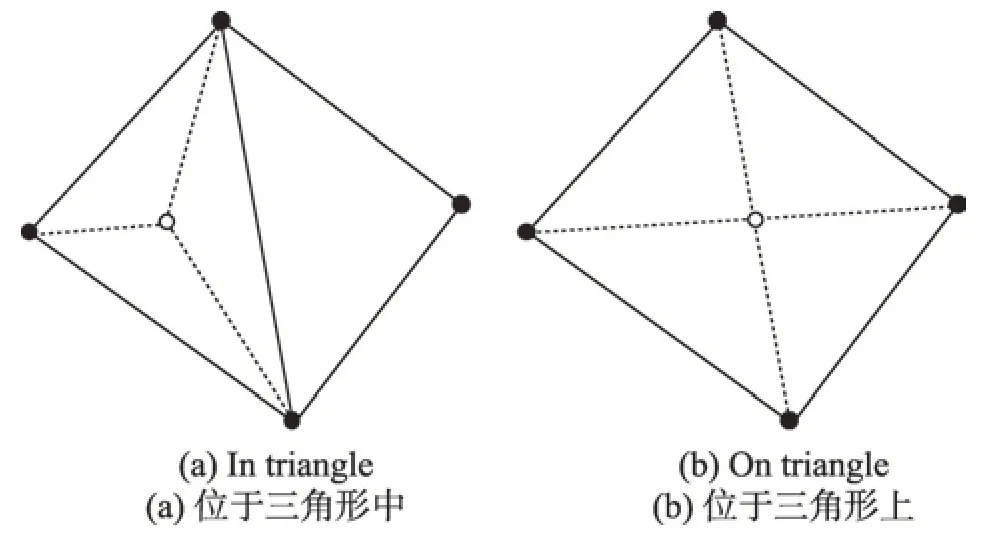
Fig.3 Generation of new triangles图3 子三角形生成示例
最后,将父三角形剩余待插点按照位置关系分配至相应子三角形内。需注意由于翻转操作的存在,父三角形可能存在多个,子三角形个数也可能大于4 个。
TID 算法会递归地分裂子三角形,当所有子三角形都不包含任何点时,本次三角剖分完成。
为减少内存使用,避免频繁的内存分配带来的时间开销,本文采用数组加链表的方式来存储待插点。该方法只使用O(n)的空间,同时其顺序访存可以有效利用起CPU 高速缓存。
3.3.5 四点共圆特例
严格的Delaunay 三角剖分不允许存在4 点共圆的情况,但共圆情况在地球系统模式网格中却无法避免,甚至是经常出现的。例如,在地球系统模式中最常用的经纬网格中,经度或纬度值相邻的4 个格点均共圆。该情况下三角剖分会存在多种合法解。这会给算法行为带来不确定性,若用于并行计算,则会给其带来串并行不一致的风险。本文针对这种情况,使用了与PatCC1[9]相同的特殊判断规则:
四点共圆合法性给定两个相邻三角形及其二者的顶点,若该4 个顶点共圆,则当且仅当该4 点中的最左点(若存在多个最左点则为最左下点)不被这两个三角形共享时,这两个三角形是合法三角形。
3.3.6 索引矩阵参数公式
给定n个原有点和m个新增点,对于TID 算法,三角剖分动态更新阶段的时间复杂度为:

给定k×k的索引矩阵,本文称k为索引矩阵参数。构建该索引矩阵的时间复杂度为O(m+n),即O(n)。假设新增点在外圈均匀分布,则非空索引块位于索引矩阵的外层,非空索引块数为O(k),各索引块平均包含三角形数量为,各非空索引块平均包含新增点数为,因此索引矩阵法的定位复杂度为上述三者之积,即。
为保证效率,本文要求索引定位法的时间复杂度既不高于构建索引矩阵的时间复杂度,也不高于三角剖分动态更新的时间复杂度,即:
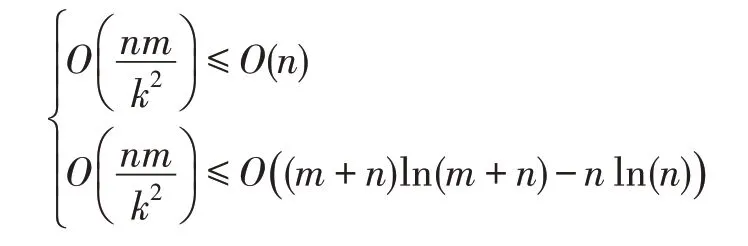
本文选取满足上述条件的最小k值作为最优索引矩阵参数K,可以表示为:
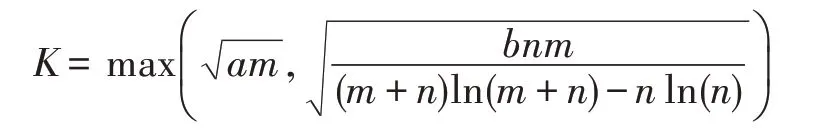
其中,a与b为系数,可通过实际测试得来。
4 性能评估
本文的性能评估主要包括:核心三角剖分性能评估和增量场景下的性能评估。对于前者,本文以Github 上的三角剖分软件作为对照组,在非增量场景进行了TID 算法和同类算法的性能对比。对于后者,本文首先对比了增量场景下TID 算法和PatCC1 原始算法的性能差异,然后通过比较TID 算法本身在增量场景和非增量场景的性能差异,来探究增量功能带来的额外开销。此外,本文还分别针对索引矩阵参数和原有剖分外扩参数进行了相应的实验探究。
4.1 实验配置
本文全部实验均在个人电脑上完成,其装有Intel Core i9-9900K 8 核3.6 GHz 处理器,32 GB 内存,可执行程序均使用GNU 6.3.0 编译器在O3 优化等级下进行编译。
本文的实验网格采用了3 种不同密度,粗、中、细,以及3 种不同类型,随机生成网格、均匀网格、真实网格。其中真实网格选取了地球系统模式中的球面立方网格作为实验数据。
实验共使用了3 种不同插点方法:
(1)非增量式:一次性加入所有点并生成三角剖分。
(2)单次增量式:将点分为两组,依次加入并生成三角剖分。
(3)多次增量式:将点分为多组,依次加入并生成三角剖分。
4.2 核心三角剖分性能
核心三角剖分即TID 算法整体流程的第5 步。本实验的对照组为Juannavascalvente 的三角剖分软件(https://github.com/juannavascalvente/Delaunay,后称Juan 软件),其使用基于Delaunay 树定位的插入式算法。本实验使用非增量式插点方法,分别统计了两者在不同类型、不同分辨率的网格下的三角剖分耗时。该耗时只包括核心三角剖分过程,去除了文件输入输出等无关过程的影响。
实验结果如表1,表中Timeout 代表实际执行时间超过1 h,OOM(out of memory)代表程序执行时耗尽系统内存。可以看出TID 算法在每个网格下的计算效率均优于Juan 软件,同时网格规模越大,TID 算法的优势越明显。因此,TID算法所采用的分解定位法在运行速度和内存占用上均优于Delaunay树定位法。
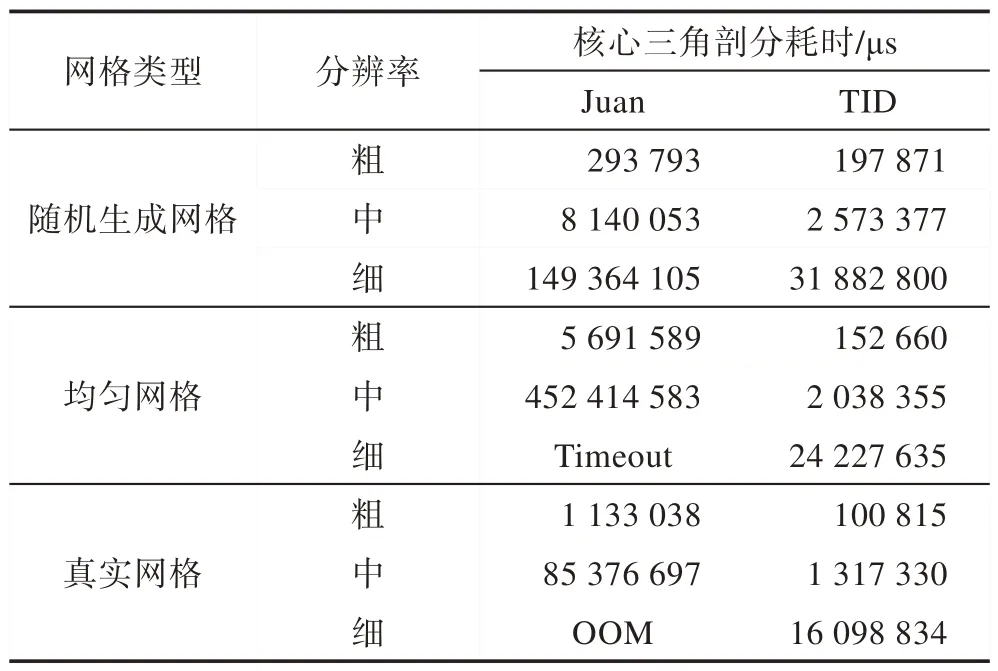
Table 1 Comparison of kernel triangulation time between Juan algorithm and TID algorithm表1 Juan 和TID 算法核心三角剖分耗时
4.3 索引矩阵参数实验
索引矩阵参数决定着新增点定位的效率。为确定3.3.6 小节中最优索引矩阵参数公式的系数a、b,本节使用单次增量插点法基于多种分辨率的随机生成网格进行了探究。
本文分别在粗网格、中网格、细网格下使用不同的索引矩阵参数测试了新增点定位的整体耗时。测试结果如图4 所示,其横坐标为索引矩阵参数,纵坐标为新增点定位耗时进行归一化后的结果,即实际耗时除以该网格下的最低耗时。

Fig.4 Tendency of locating time with indexing map parameter using various grids图4 多种网格下定位耗时随索引矩阵参数变化趋势
从图4 中数据可以看出,随着索引矩阵参数逐渐增大,各网格新增点定位耗时均呈现先减小,后增大的趋势。这主要是因为索引块较少时,每个索引块内点数及三角形数量过多,块内定位的开销仍比较大,随着索引矩阵参数增大,这样的开销越来越小。但当索引矩阵参数过大时,过于密集的索引矩阵导致单索引块中所含点数及三角形数量很少,在进行块内定位时会产生较多Cachemiss 现象,反而拖慢定位速度。从图中可以看出,粗、中、细网格的最优矩阵参数分别为30、70、100。本文规定定位耗时不超过最低耗时0.1 倍的部分为最优区间,则上述网格的最优区间分别为[21,37]、[40,140]、[70,300]。
综合粗、中、细网格的原有点数、新增点数及索引矩阵参数最优值,本文尝试不同的系数配置,并最终确定了合适的系数配置,a为0.2,b为0.3。该系数配置可以保证3 个网格下的公式推测值均落入最优区间中,如表2 所示。为进一步验证公式准确性,本文构造了点数更多的随机生成网格作为验证网格,并测试了其不同索引矩阵参数下的定位耗时,结果如图5。该网格的公式推测值也在表2 中一并列出,可见推测值仍位于图中的最优区间内。
4.4 原有剖分外扩参数实验
本节探究了3.3.2 小节中外扩参数对新增点定位耗时和三角剖分动态更新耗时的影响。该实验使用单次增量插点法,基于细密度的随机生成网格,索引矩阵参数采用4.3 节中测试出的最优值100。实验分别统计了多种外扩参数下两个主要阶段的耗时,并记录了非空索引块数量占总索引块数量的比重。

Table 2 Prediction of optimal indexing map parameters using grids with different resolution表2 不同分辨率网格下最优索引矩阵参数的推测

Fig.5 Tendency of locating time with indexing map parameter using very fine grid图5 极细网格下定位耗时随索引矩阵参数变化趋势
测试结果见表3,随着外扩系数的增大,新增点定位耗时的增加非常明显,这是因为外扩系数增大会导致索引矩阵范围的增大,进而导致新增点位于越来越少的索引矩阵块中,索引效率降低,这可从非空索引块占比的逐渐降低中看出。另外,三角剖分动态更新耗时随着外扩系数的增加而轻微增加,这主要是因为剖分范围的增大导致外层三角形被“拉长”,新增点在单个三角形中的分布不均匀,进而导致三角形的分裂次数增多,耗时增加。由该实验可知,为保证程序运行的高效性,应使用尽量小的外扩参数。
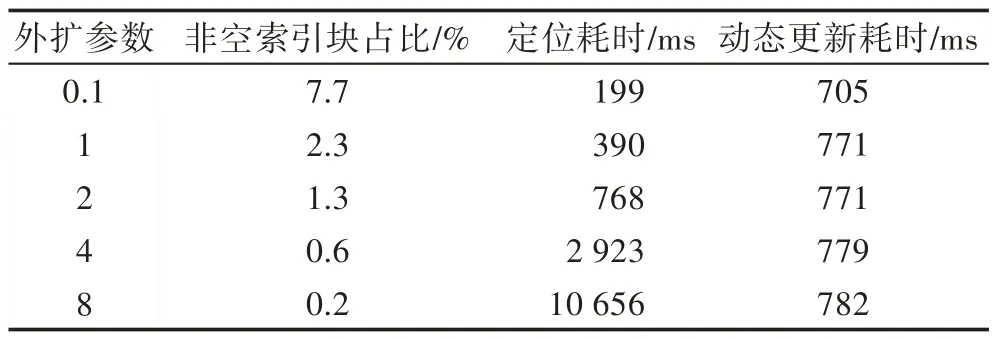
Table 3 Running time of two main steps using different expansion parameters表3 不同外扩参数下的两个主要阶段耗时
4.5 增量场景整体性能
增量场景的性能实验由两部分组成:TID 算法与PatCC1 原始算法对比实验、增量开销实验。这两个性能实验均将输入点分为10 组,每组的点数均已在结果表格中给出。
PatCC1 在更新三角剖分时采用了删除原有剖分并重新求解的方法,本文以该方法作为对照组,使用多次增量式插点方法进行了性能对比实验。结果如表4,TID 算法相比PatCC1 原始算法具有很明显的速度优势。可见若将TID 算法用于PatCC1 中,将会给其带来较大的性能提升。

Table 4 Comparison of triangulation time between TID algorithm and PatCC1 algorithm表4 TID 算法与PatCC1 原始算法增量三角剖分耗时
增量插点功能的引入也会带来额外开销,其主要来源于索引矩阵的构建及新增点的定位。为探究该开销大小,本文分别统计了TID 算法对相同网格采用不同插点方式(非增量式和多次增量式)时的耗时,实验结果见表5。表中序号n对应的增量单次耗时即为增量插入第n组新点并更新三角剖分所消耗的时间,非增量耗时即为将第0 组到第n组的所有点一次性插入并进行三角剖分的耗时。假设当前增量耗时为Tinc,上一次非增量耗时T0,当前非增量耗时Tc,则额外开销占比。从结果中可以看出,增量功能并不会引入过多额外开销,其在较好情况下与非增量式的耗时基本相近,在较坏情况下额外开销仍低于10%。
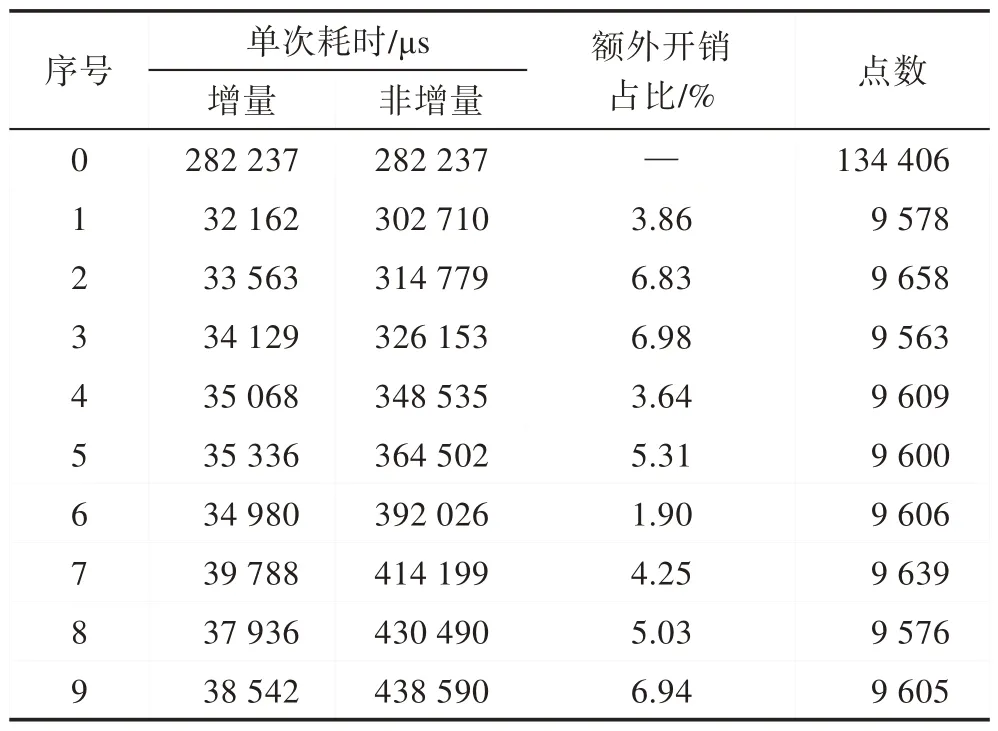
Table 5 Comparison of triangulation time between incremental TID algorithm and non-incremental TID algorithm表5 TID 算法增量式与非增量式三角剖分耗时
5 总结
本文基于分解定位插入法设计了一种高效的增量三角剖分算法TID,该算法支持在已有三角剖分基础上增加任意位置的点并更新三角剖分。该算法不仅具有增量插点特性,其与同类非增量软件相比也具有更高的计算效率。此外,合法化特殊规则的引入确保该算法能够生成唯一的三角剖分结果。
TID算法现已成功用于并行三角剖分软件PatCC1。TID 算法源代码见https://github.com/WireFisher/TID。
