巧变构学材妙阻负迁移
2020-01-04易文华
易文华
变构学材,指教师基于儿童视角和立场,依据自己的学科理解和教学风格,从学生已有的认知出发,对以教材为主的教学资源进行挖掘、整合、拓展,在合乎教育教学规律和学生学习规律的基础上,重组学习内容(学材)结构、优化课堂(呈现)结构、变调要素(关系)结构等,形成适合学生自主学习的材料。《整式乘法——完全平方公式》是人教版八年级上册第十四章第二节第二课时的内容。学生之前学习了整式的乘除法和平方差公式,并能运用法则和公式进行计算,但某些旧知识会对学生学习完全平方公式有负迁移的影响,教师可以变构学材,有效阻止负迁移。
一、预见负迁移,在知识发生点变构学材
学生学习完全平方公式,受积的乘方公式(ab)2=a2b2负迁移的影响,极易错误地认为(a±b)2=a2+b2。因此,筆者没有采用教材上从特殊到一般的方法归纳公式,而是在知识发生点变构学材,设计了一个故事作为引入:一天,聪明的阿凡提向一个贪婪的财主提出用两块边长分别为a和b的正方形土地换他的一块边长为(a+b)的正方形土地,财主心想:“一块土地换两块,划算!”,当即表示同意。几日后,财主怒气冲冲地找到阿凡提要求取消之前的交换,但阿凡提又提出用一块边长为(a-b)的正方形土地换回财主的两块正方形土地。财主心想:“上回一块地换他两块地吃了亏,这回两块地换一块地,应该不吃亏,就这么定了!”,于是财主完成了第二次交换,阿凡提脸上露出了微笑。
笔者提问:“财主为什么怒气冲冲?阿凡提脸上为什么露出了微笑?”学生马上会比较第一次交换中阿凡提的土地面积a2+b2,财主的土地面积(a+b)2,猜想(a+b)2比a2+b2大,财主因为吃亏了,所以怒气冲冲。第二次交换中阿凡提的土地面积是(a-b)2,财主的土地面积是a2+b2,猜想(a-b)2比a2+b2小,阿凡提占便宜了所以露出了微笑。学生从故事中抽象出数学问题后,笔者再引出本节课的课题:完全平方公式。
笔者通过引入故事,激发学生的学习兴趣,引发了学生的数学思考,即把(a+b)2、(a-b)2与a2+b2进行比较,猜想它们不相等,遵循了完全平方公式的自然生成过程,让学生体会知识发生的必要性、合理性。
二、弱化负迁移,在知识生长点变构学材
故事引入使学生初步建立(a+b)2、(a-b)2和a2+b2在数量上不相等的感性认识,但它们之间是怎样的数量关系呢?笔者设计了三个活动弱化负迁移,在知识的生长点变构学材对他们的认知结构进行重组与改造。
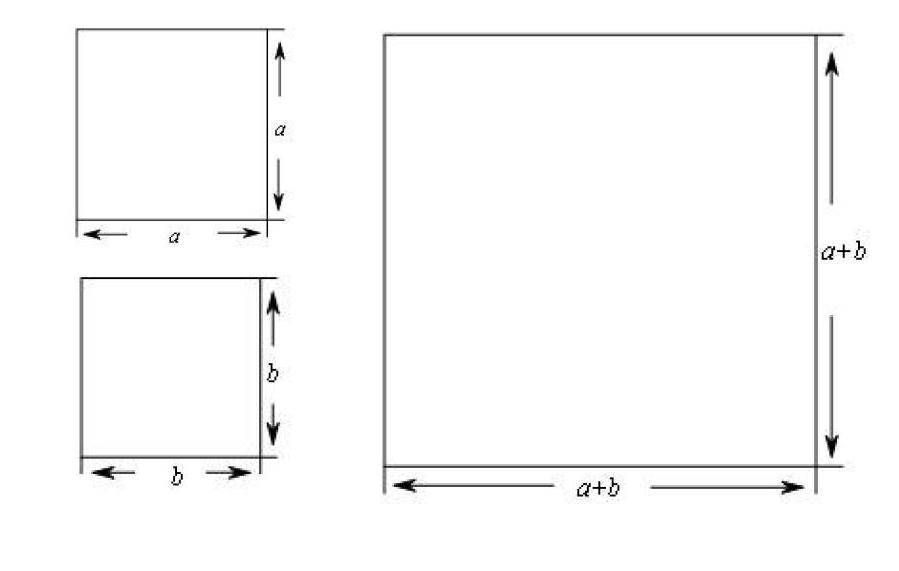
笔者先把事先准备的边长分别为a和b的小正方形纸片发给学生,让他们动手拼图,比较这两个小正方形纸片的面积与右图的大正方形的面积,写出大正方形面积与两个小正方形面积之和的数量关系(如下图)。
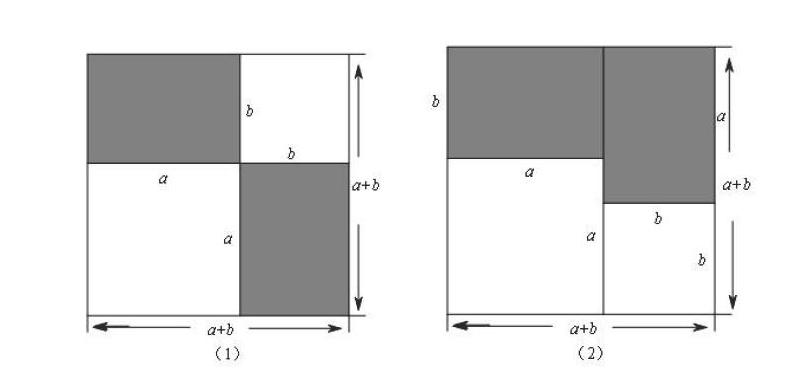
接着,笔者指名学生带着学案到讲台分享自己的发现。一名学生把两个小正方形按对角的方法放在右图中的大正方形里,发现(a+b)2比a2+b2大,大两个长方形的面积,即2ab。另一名学生把两个小正方形并排放,也发现(a+b)2比a2+b2大,大2ab。笔者追问:“(a+b)2与a2+b2之间是怎样的数量关系?”学生齐答:“(a+b)2=a2+2ab+b2。”笔者继续追问:“通过拼图探究的结论来看,我们对财主怒气冲冲的猜想是正确的,那么财主吃了多少亏呢?”学生回答:“2ab。”
笔者让学生动手实践,拼一拼,探究(a+b)2与 a2+b2的数量关系,通过分享探究成果,培养学生的动手能力、小组合作交流意识和语言表达能力,发展了学生的符号意识。在探究的过程中深刻体会和的完全平方公式,弱化积的乘方公式(ab)2=a2b2的负迁移,原来(a+b)2=a2+2ab+b2。
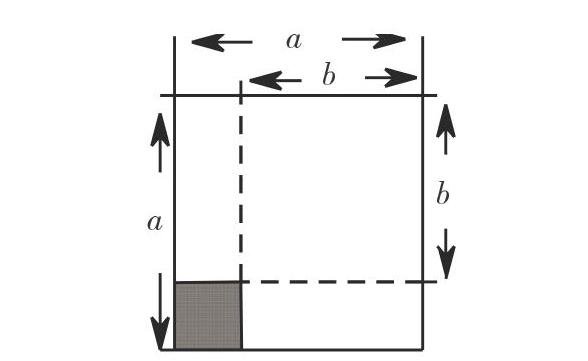
对于(a-b)2=a2-2ab+b2的探究,笔者预设了两个方案。第一个方案是提问:“我们知道了(a+b)2=a2+2ab+b2,那么(a-b)2=?”没有学生能把(a-b)2转化为[a+(-b)]2,利用和的完全平方公式计算。于是笔者启动了第二个方案:如下图,将边长为a的正方形的边长减少b,得到一个小正方形(阴影部分),请用两种不同的方法表示小正方形的面积。
①直接表示方法 ,
②间接表示方法 。
比较小正方形面积与a2+b2的数量关系,写出结论。
学生很容易发现直接表示是(a-b)2,笔者请学生带学案到讲台讲解间接表示方法。一名学生说:“阴影部分的面积等于大正方形的面积a2减去上面的长方形面积ab,再减去右下角的长方形面积b(a-b),也就是等于a2-ab-b(a-b)。”另一名学生说:“阴影部分的面积等于大正方形的面积a2减去右上角的正方形的面积b2,再减去左上角和右下角的两个长方形的面积和2b(a-b),也就是a2-b2-2b(a-b)。”还有一名学生说:“阴影部分的面积等于大正方形的面积a2减去上面长方形的面积ab,再减去右边长方形的面积ab,右上角的小正方形被减了两次,所以再加上它的面积b2,也就是a2-ab-ab+b2= a2-2ab+b2。”笔者适时追问:“(a-b)2与 a2+b2的数量关系是什么?通过拼图探究的结论来看,我们对阿凡提露出微笑的猜想也是正确的,那么阿凡提占了多少便宜呢?这个故事又告诉我们什么?”学生齐答:“ (a-b)2 =a2-2ab+b2,从阿凡提的故事中体会到要学好数学,像阿凡提一样多思考。”
学生在a>0、b>0的前提下根据图形面积验证并理解了结论的几何意义,但完全平方公式归根结底还是一个代数公式,教学中还原其代数属性不可或缺,笔者认为这也是为什么在差的完全平方公式探究方案一中学生没有想到用转化思想“差化和”达成预设的重要原因。接下来,笔者让他们从代数运算的角度证明结论的一般性,即a、b为任意实数时的情形,从特殊到一般的探究经验才能落地生根。在学生演板后,笔者追问:“代数运算推理的依据是什么?”最后学生明确算理:完全平方公式推导依据是多项式乘多项式的法则。
学生经历了完全平方公式的发生和生长过程,笔者又设计了如下问题:
完全平方公式的结构特征:
①公式的左边是 ;
②公式的右边有三项, ;
请用文字表达完全平方公式 。
学生对公式的结构特点进行细致地分析再认,并进行文字表达,从符号语言到文字语言的切换,使语言表达能力得到了培养,对完全平方公式的认识由深入到深刻。
(作者单位:武汉市蔡甸区新农中学)
