刚塑性材料第二变分原理的证明研究及应用

任 杰，孙贺磊，李加欣，郭宝峰,*

(1.先进锻压成形技术与科学教育部重点试验室(燕山大学)，河北 秦皇岛 066004；2.上海电机学院 高职学院，上海 200240 )

0 引言

塑性力学广泛用于金属结构分析与金属塑性成形的分析计算，在金属结构的塑性力学分析中，内部应力场的分布状况是评定结构布局好坏的重要依据，借助应力场可以确定结构的极限载荷及安全程度。金属塑性成形是基于金属学与塑性力学的学科，变形金属内部应力场的计算是金属塑性成形的基础分析之一，利用应力场可以预测变形体内部新缺陷的产生与原有缺陷的修复，确定成形载荷的大小。

在塑性变形问题的应力场求解中[1]，出现了两个分支，一是以满足实际工程问题需要为目的简化解法，如主应力法(又称为工程法或者切块法)[2-3]、变形功法(又称为功平衡法)[4]、下限法[5-6]等，这些方法主要用于近似地计算塑性变形工程问题的载荷，不追求塑性变形体内部应力场分布的准确性，人们常常称之为工程解法。二是寻求精确解的方法，有全部塑性力学方程直接联立求解法、特定条件下专门解法(刚塑性材料平面变形的滑移线法[7]、塑性条件与平衡方程联立求解法)、塑性力学的变分解法[8-11]等。直接联立求解法需求解一个偏微分方程组，有着巨大的数学困难，这种求解法尚未有文献的报道。特定条件下的专门解法因又受条件限制，仅能用于少数问题的计算。塑性力学的变分解法的优点逐渐被人们所认识，它的计算过程中的数学难度相对小，且又不失结果的准确性。

塑性力学的变分解法和有限元解法是建立在塑性力学的变分原理的基础上发展起来的。理想刚塑性材料是塑性力学中最基本和应用最广泛的材料模型之一，如金属的热塑性变形材料模型。对于理想刚塑性材料建立的第一变分原理和第二变分原理，前者用于变形分析计算，如速度场、位移场，进而求得应变速率场等。然而，由于体积不变条件的限制，不能通过本构方程，再由应变速率场计算得到应力场。求解应力场只能用第二变分原理。目前，刚塑性材料的第二变分原理的证明是利用Drucker公设和求极值的方法进行的[12]，无论是从定理证明方法的合理性，还是从应用定理求解问题的方法看，都需要进一步完善。本文给出一种新的证明方法，即利用数学的泛函变分理论进行证明，并给出定理求解实际问题应用的范例。

1 刚塑性材料的第二变分原理证明研究

1.1 刚塑性材料的第二变分原理

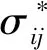
(1)

1.2 刚塑性材料的第二变分原理的证明

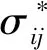
(2)

(3)

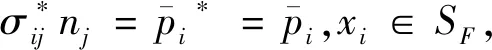
(4)

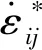
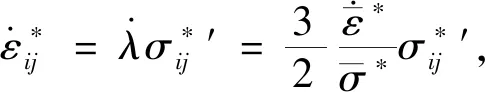
(5)

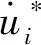
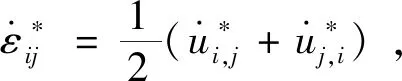
(6)

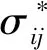
(7)

因为

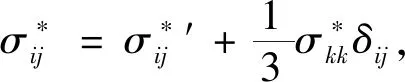
(8)

将式(8)代入式(7)得

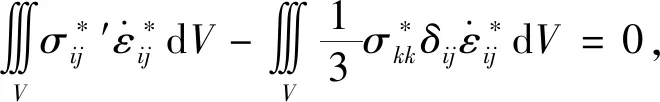
(9)

因此，将式(9)代入(1)得

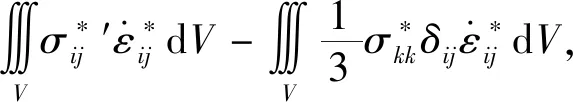
(10)

因为

则

(11)

将式(11)代入式(10)，得

(12)

(13)

于是，式(13)化简为

(14)

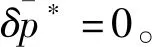
(15)

(16)

2 平面镦粗应力场的计算

平面变形的镦粗[14]除具有理论意义外，也是生产中常见的塑性力学问题，如板条的精压、连杆锻件的整形精压等。平面变形镦粗的力学模型如图1所示。

图1 平面变形镦粗的力学模型Fig.1 Mechanical model of upsetting in plane deformation

2.1 端面摩擦的设定

τ(x)=a0+a1x+a2x2，

(17)

由力的边界条件得

当x=0时，τx=0=0；

当x=b时，τx=b=0；

当x=x0时，τx=x0=-τk，

将以上4个条件代入式(17)得

(18)

将式(18)代入到式(17)，得

(19)

2.2 静力学许可的应力场的设定

由于平面镦粗的坯料的宽度b远大于高度h，故取τxy与y为线性关系。设

τxy=Dyτ(x)，

(20)

已知，当y=h时，τxy=τ(x)，则

(21)

将式(19)和式(21)代入式(20)，得

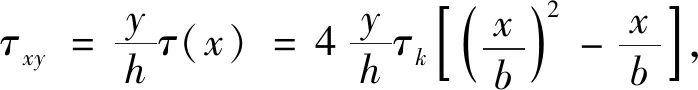
(22)

将式(22)代入平衡微分方程

得

(23)

(24)

对式(23)和式(24)分别求积分，得

(25)

(26)

式中，M(y)、N(x)为积分的任意函数，M(y)可由力边界条件确定如下：

当x=b时，σx=0，代入式(25)得

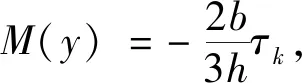
(27)

将式(27)代入到式(25)中，得到一个平面镦粗矩形截面的应力场

(28)

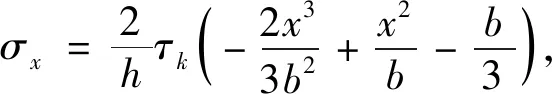
(29)

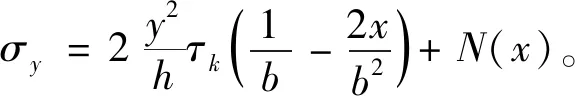
(30)

由于任意函数N(x)满足应力场函数的一般运算条件，可用多项式形式表示，即N(x)=c0+c1x+c2x2+c3x3+……+cnxn，本例中取前两项，即取

N(x)=c0+c1x。

2.3 真实应力场的确定

平面镦粗的真实应力场可借助刚塑性材料第二变分原理确定。为使应力场为静力学许可的，利用Lagrange乘子法[8]求解。设定约束条件，即应力场满足Mises屈服准则：

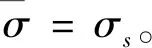
(31)

等效应力

对于平面应变问题，有

简化等效应力，得

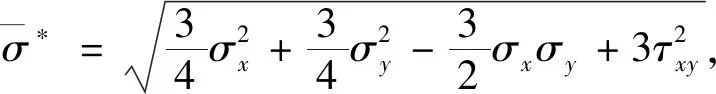
(32)

设约束条件

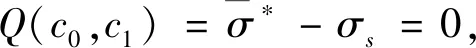
(33)

利用Lagrange乘子法，在此引入Lagrange乘子γ，设目标函数

(34)

将式(1)、(28)～(30)、(32)和(33)代入式(34)，得

(35)

式中，

为便于式(34)中的第二项的运算，运用布尼亚科夫斯基不等式[12]

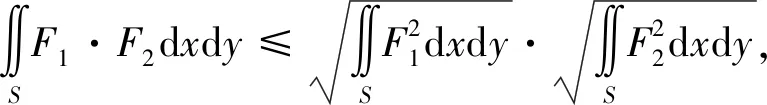
(36)

现令

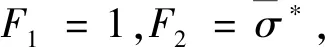
(37)

将式(37)代入式(35)中的第二项进行简化得

(38)

将式(38)代入式(34)并进行运算，得

式中，

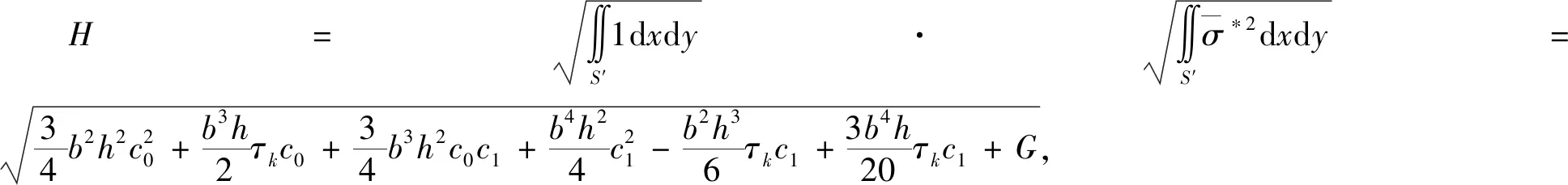
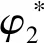
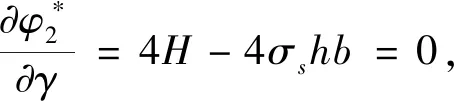
(39)

(40)

(41)

整理式(39)得

(42)

联立式(40)和(41)得

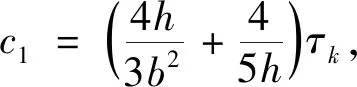
(43)

将(43)式代入(42)，得

(44)

将式(43)和式(44)代入到式(30)中，得到平面变形的镦粗的真实应力场为

(45)

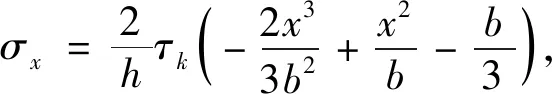
(46)

(47)

2.4 计算结果的讨论

2.4.1端面无接触摩擦

当端面无接触摩擦力，即τk=0时，代入式(45)～(47)得

当端面无接触摩擦时，上述应力场与文献[15]的结果一致，表明得到的应力场是正确的。

2.4.2端面存在接触摩擦

当存在端面的接触摩擦时，由图2、图3和图4可得到各截面上的应力分布。本文克服了文献[15]许多不足：1)端面摩擦的设定分布更符合实际的镦粗情况，对称面x=0和自由表x=b上的摩擦应力都为零；2)保证了在x=b整个界面上σx=0，满足了该面上的边界条件；3)τxy既是y的函数，也是x的函数。

图2 xoz截面(y=0)上的应力分布Fig.2 Stress distribution on xoz section(y=0)

图3 端面(y=h)上的应力分布Fig.3 Stress distribution on the end face(y=h)

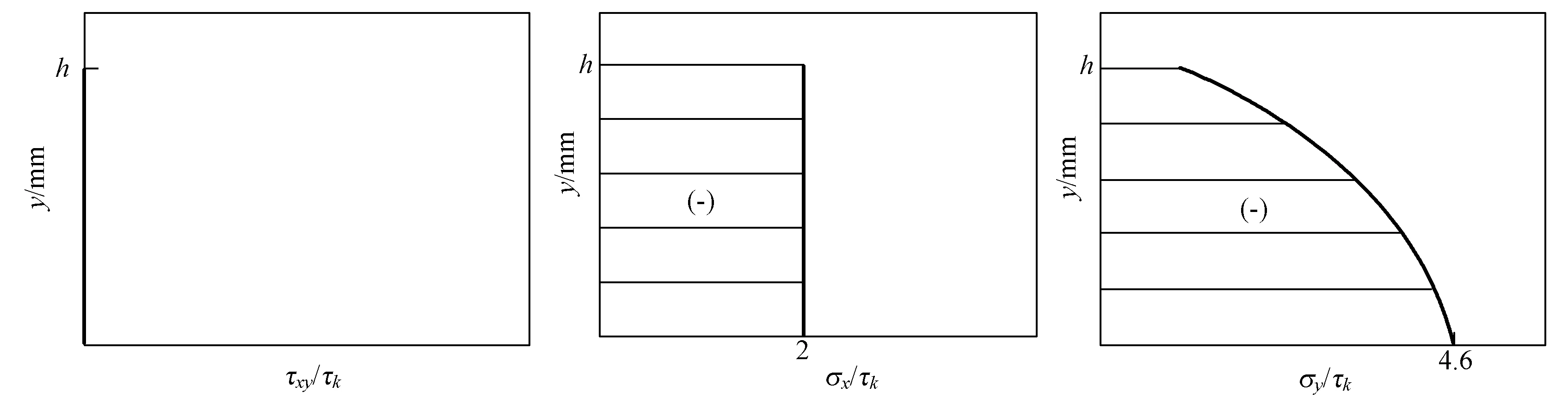
图4 yoz截面(x=0)上的应力分布Fig.4 Stress distribution on yoz face(x=0)

3 结论

1) 利用泛函变分给出了刚塑性材料第二变分原理证明的一种新方法，更明显地体现了刚塑性材料第二变分原理的力学意义，也示范了利用该定理求解的过程。

2) 借助刚塑性材料的第二变分原理，计算了接触面存在摩擦条件平面镦粗的应力场，结果分析表明得到的应力场是正确的，进一步完善了现有文献应力场解析结果的不足。