基于小生境和模糊理想决策的冷热电联供系统光伏容量配置

魏 征，耿跃华，*，迟福建，孙 阔

(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北工业大学 电气工程学院，天津 300130；3.国网天津市电力公司，天津 300055)

0 引言

冷热电联供(Combined Cooling,Heating and Power，CCHP)系统属于分布式能源系统，是未来综合利用多种能源的分布式电源发展的重要方向，也是区域能源互联网的一种具体表现形式[1]。我国CCHP发展起步较晚，综合能源的利用率较低。随着分布式发电技术以及天然气的利用率在一次能源中比重不断升高，我国CCHP项目也在不断建设中。

在CCHP系统规划的相关研究中，文献[2]以最小化总能源消耗作为总体目标，建立了系统的线性模型以得出CCHP系统的最佳配置。文献[3]对燃气轮机与地下水地源热泵组成的复合供能系统分别以年费用最低和天然气耗能最小为优化目标进行优化配置和运行规律的研究。文献[4]提出兼顾经济性和综合能效的多目标优化模型对含CCHP系统的区域多微网进行求解，使得系统在保证综合能效的基础上提高经济性。文献[5]建立了含光伏和蓄能的CCHP系统调峰调蓄优化调度数学模型,以最小化经济成本和电网供电方差为目标进行经济调度。文献[6]以系统的购电成本、燃料成本、分布式能源等年值成本及年运行维护成本作为优化调度目标，采用线性整数规划方法进行优化调度。

CCHP系统中的光伏接入一方面可以有效降低系统的运行成本，减少天然气消耗和网购电量；另一方面，由于光伏出力本身具有一定的波动性和间歇性[7]，光伏接入也会影响CCHP系统的运行。因此，有必要综合考虑光伏接入影响进行优化配置。本文提出了一种面向CCHP系统的光伏容量优化配置方法，首先分别建立了光伏出力和CCHP系统模型，以光伏改造经济收益和用户满意最大为两个目标函数建立多目标优化模型，应用小生境粒子群算法对改造方案进行多目标求解，使用模糊理想决策方法对得到的非劣解集进行决策得到CCHP系统的最佳光伏配置容量。最后，以中国北方某工业园区为例验证了本文所提出规划方法的有效性。

1 光伏出力及CCHP系统的数学模型

本文涉及的区域能源互联网的改造方案以带有新能源设备的冷热电联供系统为对象，其中新能源设备为光伏发电系统。本节主要建立光伏数学模型和CCHP系统的数学模型。

1.1 光伏系统出力模型

光伏电池输出功率主要受天气等自然条件影响，影响因素包括季节、太阳辐射强度、天气类型、温度等。通常可用式(1)计算光伏电池输出功率[7]：

PPV=PRfPV(GT/GST)(1+ap(TC-TST)),

(1)

式中，PR表示光伏组件的额定功率；GT与GST分别为当前情况和25 ℃时的辐射；ap为事先确定的因子；fPV为影响系数，通常是0.8～0.95之间的一个常数；TC与TST分别为组件实际温度值和25 ℃的标准温度；组件的实际温度TC为

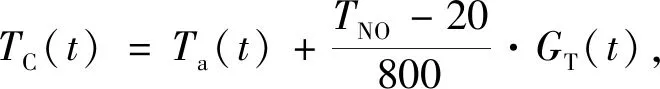
(2)

式中，Ta环境温度；TNO是42～46 ℃之间的一个常数。

1.2 CCHP系统出力模型

图1为CCHP系统的整体出力模型和能量流动模型，各个部分间的出力关系为

式中，PL、CL和HL分别为客户需求的电、热和冷的功率。此处假定CCHP系统功能应始终满足客户不同时刻t的动态功率需求；Pgrid、Pgas和PPV分别为电网功率、燃气轮机电功率和光伏出力；Hw、Hwy和Hwg分别为燃气轮机余热、余热锅炉和燃气锅炉的热功率；Hwc和Hwh分别为输入吸收式制冷机和热交换机的功率；ηP、ηC和ηH分别为电、热和冷的能源传输或转换效率；ηGP和ηGH分别为燃气轮机和燃气锅炉运行效率，前者主要与环境温度有关[8]，可表示为

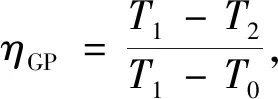
(4)

式中，T1与T2为环境系数，根据经验公式可分别取573.15 K和423.15 K，T0为环境温度。

图1 CCHP系统模型Fig.1 Model of CCHP System

2 光伏容量配置多目标数学模型

2.1 目标函数

1) 光伏改造经济收益最大

经济性是衡量规划方案的重要指标，对比光伏接入前后的系统运行状态，以光伏改造收益最大为规划目标之一。该目标可表示为

max(CCCHP-CPV),

(5)

式中，CCCHP为光伏改造收益；CPV为光伏建设运行成本。其中，改造成本主要为光伏建设运行成本:

(6)

式中，CPV表示光伏容量；λins为光伏设备单位装机成本；r0为贴现率；a为光伏设备运行年限；α为光伏运营成本和建设成本的比值，一般取5%。

光伏接入后，可以减少用户的网购电量和天然气消耗，在以热定电的CCHP运行模式下，假定光伏仅供自发自用，该部分的收益可表示为

(7)

式中，PPV(t)为光伏在t时刻的出力；N为仿真周期；pp为网购电价；其中，PPV的出力取决于光照状况，如式(1)所示；Pgas取决于系统对于冷热负荷的需求。

2) 用户满意度最大

用户满意度分别由经济满意度和供能满意度构成。其中经济满意度主要用于衡量光伏弃电量占总电量的比例，当弃电量太高时，即认为规划方案不合理，其表达式为

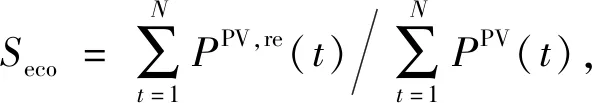
(8)

其中，PPV,re(t)为光伏在t时刻的有效出力，可通过式(3)计算得到。

供能满意度主要用于衡量PV接入对于系统供能波动的影响，当光伏接入比例过大时，认为光伏出力波动将会影响整个CCHP系统的供能效率，其表达式为

(9)

其中，PPV(t)>0。

综合考虑以上两方面满意度，将其表示为

max(xSeco+(1-x)Ssup),

(10)

式中，x为权重系数。

2.2 约束条件

光伏发电系统出力特性不稳定、配电线路输送能力限制[8]等因素都会限制CCHP消纳光伏发电量的能力。出于安全考虑需对光伏发电消纳量进行约束：

0≤CPV≤CPV,max,

(11)

式中，CPV,max为光伏最大接纳量。

3 多目标优化求解流程

在多目标优化问题中，多个规划目标一般难以同时达到最优，相应的多目标求解方法包括加权方法、Pareto方法和DEA方法等，相对应的常见多目标求解算法有包括多目标蚁群算法、NSGA-II方法和多目标粒子群算法等[9]。其中，多目标粒子群算法具有较快的收敛速度，在求解此类复杂规划问题方面具有一定优势，本文选用了一种小生境粒子群法对多目标问题进行求解，得到Pareto非劣解集。在从非劣解集中选择最佳方案过程中，因各项指标的重要程度难以准确衡量，因此采用模糊理想决策方法对改进小生境算法得到的非劣解集进行辅助决策，最终得到最佳优化方案，优化策略总体框架图如图2所示。

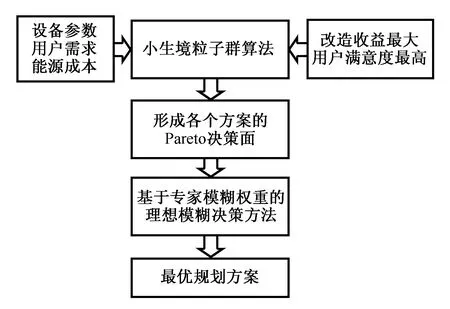
图2 优化策略总体框架图Fig.2 General framework of optimization scheme

3.1 小生境粒子群中的小生境机制

传统多目标粒子群算法在求解过程中，早期过快收敛速度容易导致算法局部Pareto最优前沿收敛，影响全局寻优。因此，本文引入小生境机制来提高多目标求解效率[10]。小生境机制中，每个个体单元可以有限共享资源,采用共享函数(Sharing Function，SH)来确定所有个体单元在小生境中的共享程度，其定义了个体间的密切程度。相似度越高的个体单元，其共享程度越高。而个体之间的相似性可以通过表现型来表示，随着小生境内个体单元数增多，每个个体单元的适应度会不断减小。通过这种方式可以使得个体单元可以分布在多模问题的不同峰值上,对任意个体Xi适应度的定义为

(12)

(13)

(14)

式中，Nm表示小生境内的个体数量；dij是个体Xi与Xj的欧氏距离；f(dij)表示个体Xi与Xj的密切程度；σshare是事先设定的共享距离；Fi表示个体Xi的种群适应度。

3.2 改进粒子群算法中的交叉和变异

在粒子群迭代的过程中对种群中适应度小的粒子进行交叉与变异的运算，检索粒子附近的非劣解。在处理多维优化问题时，该改进能有效提高粒子群算法的全局优化能力。

3.2.1交叉过程

1) 生成一个随机数，如果这个随机数大于如式(15)所表示的数值，则进行下一步。

(15)

2) 选择两个自由粒子，Xi=(xi1,xi2,…,xin)和Xj=(xj1,xj2,…,xjn)，并选择粒子位置向量的维度。

3) 令v1=xik，v2=xjk，生成一个(0,1)的随机数R，利用式(16)和(17)完成对xik和xjk的更新:

xik=R·v2+(1-R)·v1,

(16)

xjk=R·v1+(1-R)·v2。

(17)

3.2.2变异过程

1) 生成一个随机数，如果这个随机数大于式(18)所定义的数值，就进行下一步，反之就结束此次变异：

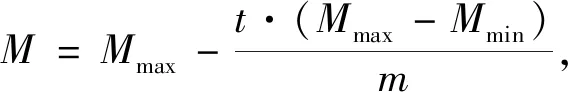
(18)

式中，Mmin和Mmax分别表示最大交叉概率和最小交叉概率。

2) 选择一个自由粒子Xi=(xi1,xi2,…,xin)，并随机选择该粒子位置向量的维度坐标xik。

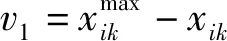
(19)

(20)

3.3 小生境粒子群算法的求解步骤

根据上述对小生境粒子群算法关键步骤的介绍，本文所提出的多目标模型求解算法的具体步骤如下：

1) 生成初始种群P0和速度V0，若初始种群中存在某一个体单元X0优于本种群一半以上的其他个体单元，则该个体即为初始最优位置Pbest=X0，否则就随机挑出一个Pbest。设置一个最优种群H，其可容纳一定数量的个体，将P0中的个体全都放入H中。

2) 计算H中个体的目标函数值，存入HG中,利用小生境共享机制计算最优种群的个体适用度，并根据适用度比例用轮盘赌法选出全局最佳位置Gbest。

3) 更新粒子群，同时更新个体最优值Pbest。根据帕累托多解的原则，用非劣解完成对H的更新，若个体数量已经超出H的最大数量，则删除那些适应度更小的个体，完成对H和HG的更新。

4) 选出H中的部分个体进行交叉变异步骤，如果运行结果显示个体非劣并且适应度优于之前所有个体，则保留本次交叉变异。

5) 若达到最大迭代次数，结束迭代当前解集作为帕累托最优解集；反之，返回步骤2)。

3.4 模糊理想决策方法

模糊理想决策方法主要思想是对权重(重要程度)进行模糊化处理，用三角模糊数来描述专家对各项指标重要程度的判断[11]。三角模糊数与专家目标权重语言变量之间的关系如表1所示。

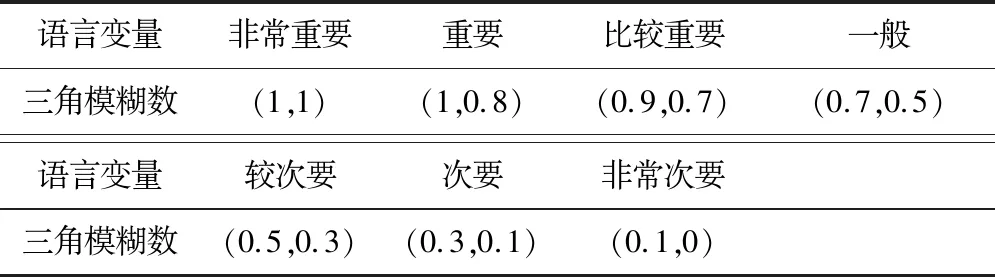
表1 三角模糊数与目标权重语言变量对应关系Tab.1 Correspondence between triangular fuzzy numbers and target weight linguistic variables

通过专家评价将规划目标从“非常重要”到“非常次要”给出模糊权重，使得模糊理想决策方法一方面可以客观的反映帕累托前沿的分布对于最优决策的影响，另一方面也可以兼顾不同目标函数重要程度的需求。

假定存在一个多目标规划问题max(f1,f2,…,fz)，共有q个专家，则利用模糊理想决策方法得到最优规划方案的过程如下：

1) 按照表1所示的重要程度，由q个专家给出f1,f2,…,fz的模糊权重，权重矩阵表示为

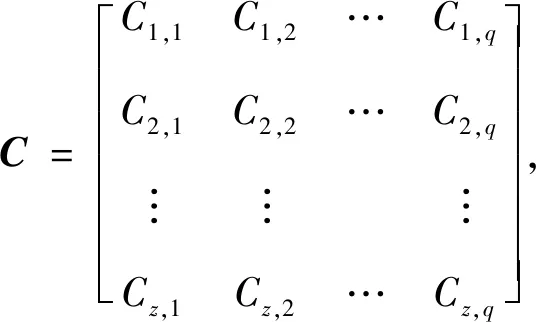
(21)

式中，Cz,q为第q个专家给出的第z个目标函数的权重。对矩阵C中的各行权重相加取平均，并做归一化处理，可得转置权重矩阵为

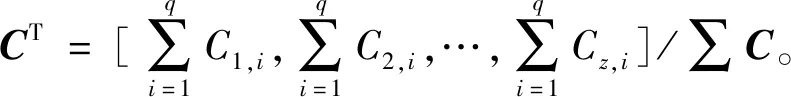
(22)

2) 将帕累托前沿中的规划方案数目记为n，则目标函数矩阵可表示为

(23)

式中，fn,z为第n个规划方案对应的第z个目标函数的值。对矩阵F中的元素进行模糊处理，对于在第x行第y列的元素，将第y行的最大值和最小值分别记为max(fy)和min(fy)，则模糊处理并加权后的fx,y值为

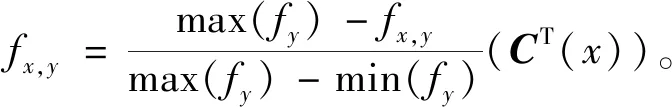
(24)

3) 形成加权后的目标函数矩阵，寻找各项目标函数统一处理后的最优值和最劣值，得到“理想最优解”(max(f1),max(f2),…,max(fz))和“理想最劣解”(min(f1),min(f2),…,min(fz)) 。

计算每个规划方案到“理想最优解”和“理想最劣解”的空间距离，当某规划方案同时满足接近理想最优解且远离理想最劣解时，该方案即为最佳规划方案。

(25)

(26)

4) 计算z个规划方案距离理想最优解和理想最劣解得相对距离，将相对距离最大的值作为最佳决策方案：

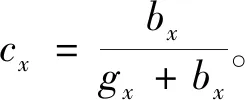
(27)

4 算例分析

4.1 场景设置

以我国北方某地工业园区为例，该园区冬季、夏季和过渡季的典型日光伏出力和温度状况分别如图3和图4。

图3 园区不同季节典型日的光伏出力特性Fig.3 Daily PV power output in typical days of different seasons

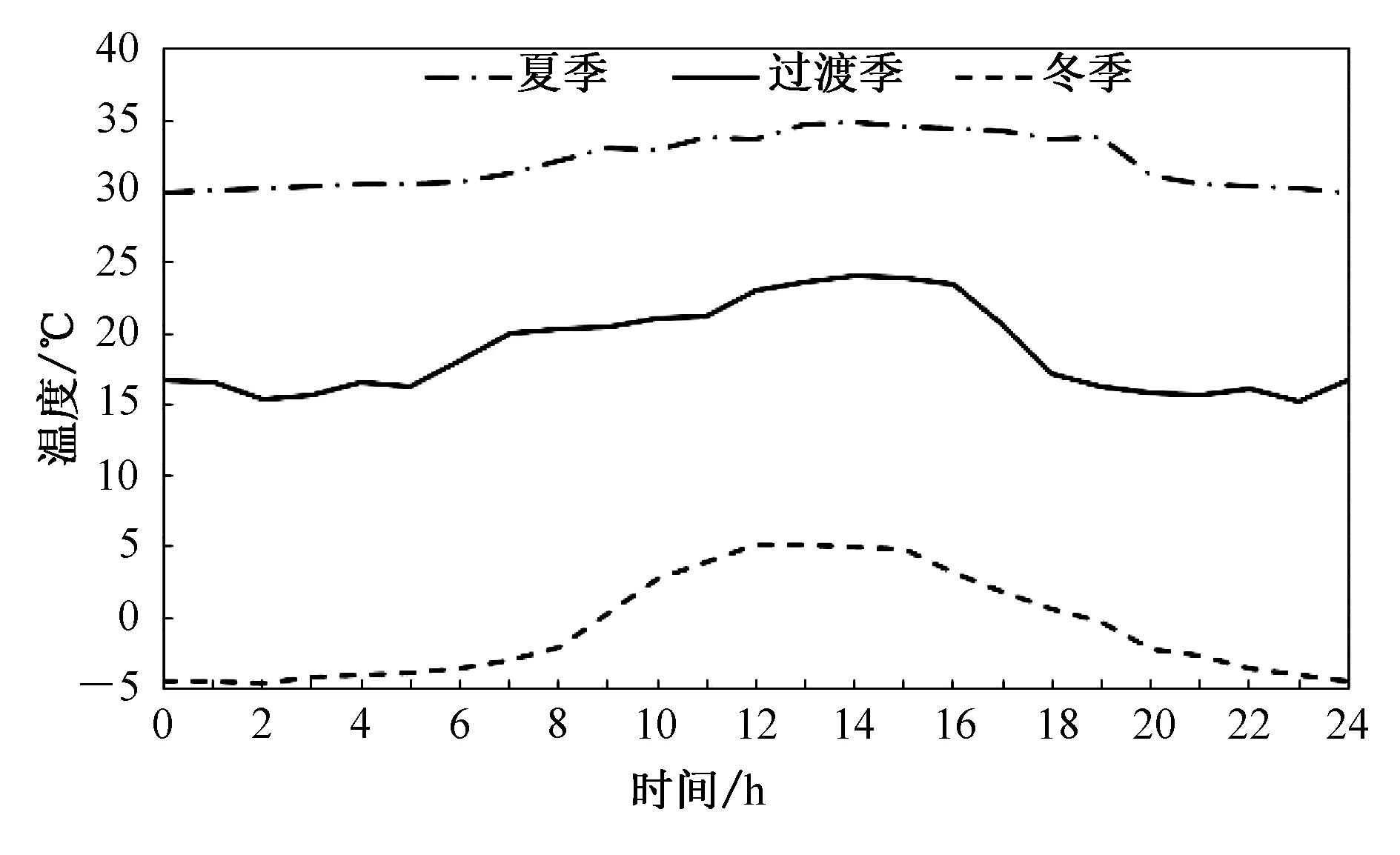
图4 不同季节典型日温度曲线
Fig.4 Temperature curve in typical days of different seasons

光伏装机成本为7.35元/W，电价为0.69元/kW·h，天然气价格为3.97元/m3。电、热和冷的能源传输或转换效率分别为0.98、0.8和0.86。燃气轮机功率为2 MW，余热锅炉为1.5 MW，吸收式制冷机为1.3 MW，燃气锅炉为1.4 MW，吸收式制冷机为1.2 MW，该园区典型的冷热电负荷需求如图5。根据文献[9]中给出的多目标函数中不同指标所占比例，本次研究中设定经济满意度和供能满意度的权重系数均为0.5。

4.2 仿真结果分析

根据本文所提出的小生境粒子群算法，按照3.3节所述的求解步骤对算例进行求解，得到Pareto前沿如图6。

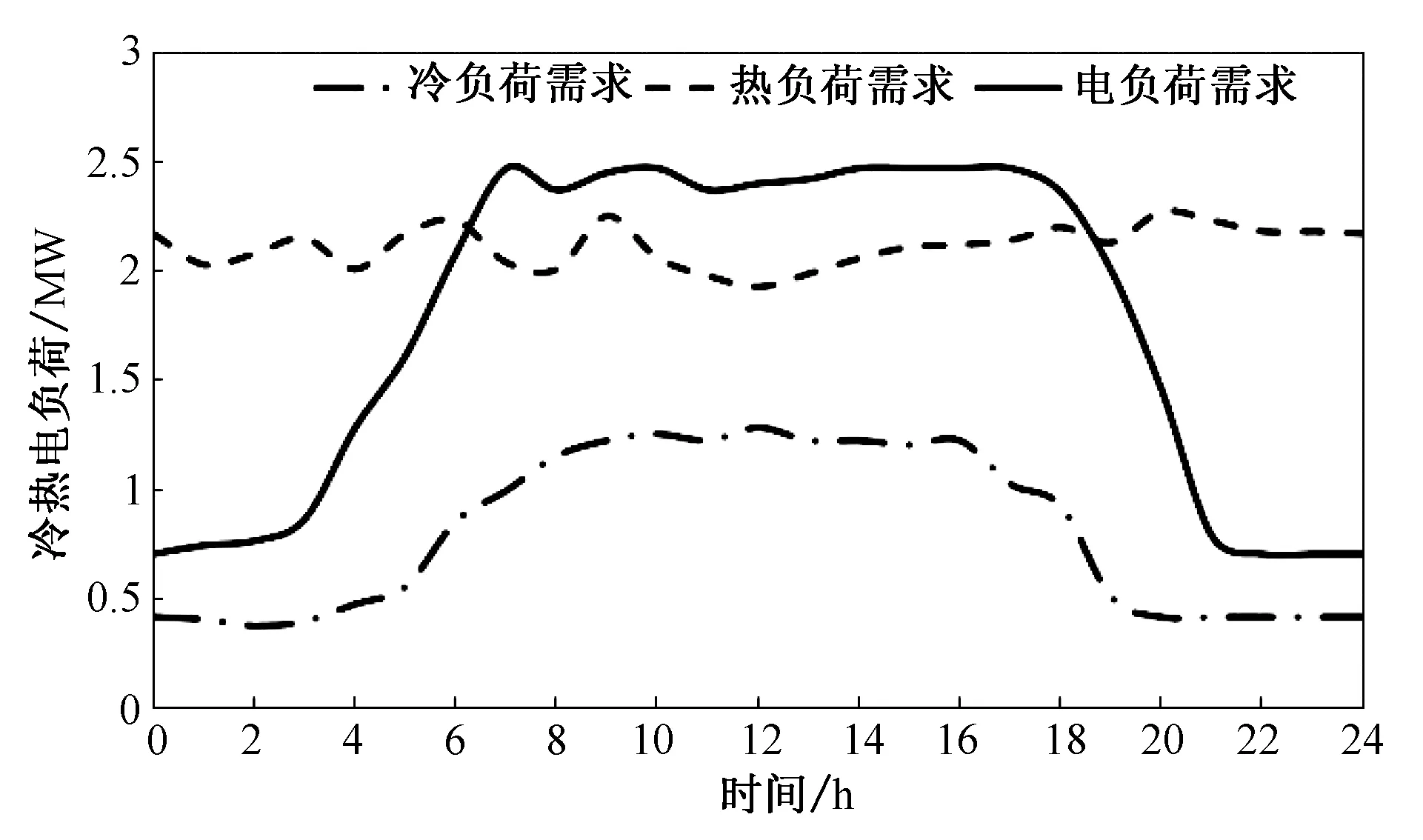
图5 工业园区典型日冷热电需求Fig.5 Cold, heat and power demand of industry park in typical days

图6 多目标Pareto前沿结果
Fig.6 Multi-objective Pareto result

分析该图可知，当用户满意度逐渐增加时，PV改造年收益逐渐降低，满意度最大值约为0.65，此时对应的PV改造年收益约为100万元；当PV改造年收益增加时，用户满意度逐渐降低，PV最大改造收益约为600万元，此时的用户满意度约为0.05。两个规划目标难以同时达到最优，将仿真结果进一步展示如图7。

图7 规划目标随PV装机量变化Fig.7 Change of planning object with PV capicity

图7中，用户满意度随PV装机量增加而加速降低，其主要原因为PV出力存在一定的波动性，PV装机量越大，对于CCHP系统总体影响越大，且随着装机量增加，弃光率逐渐上升，导致用户满意度降低。同时，PV改造收益随装机量增加而增加，当装机量为3.5 MW后，改造收益的增加速度逐渐降低，即此时CCHP系统需求对于PV需求已趋于饱和。

基于3.4节所提出的模糊理想决策方法，对所得到的Pareto前沿进行排序，将理想度前三的规划方案展示如表2。

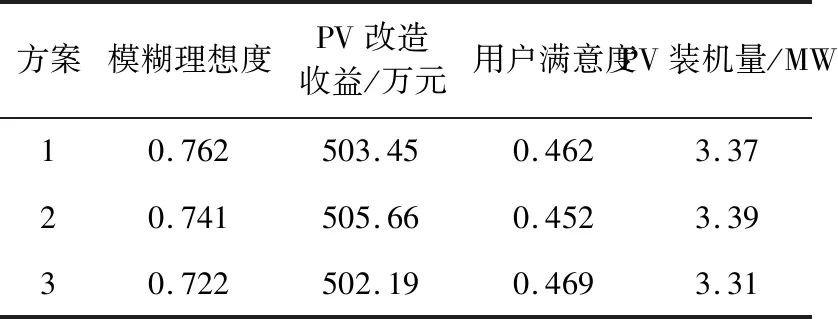
表2 模糊理想决策排序结果Tab.2 Result of fuzzy ideal decision

分析该表可知，方案2的PV改造收益为505.66万元，在3个规划方案中最高，但用户满意度较低；方案3的用户满意为0.469，在3个规划方案中最高，但改造收益相对较低；方案1两个规划目标均居中，但总体模糊理想度最高为0.762，其对应的PV出力、电网购电和燃气轮机发电情况如图8所示。

图8 PV出力、电网购电和燃气轮机发电状况Fig.8 Power of PV, power grid and gas turbine

图8中，中午时刻PV出力最大，此时基本不需要来自电网的购电和燃气轮机发电；夜间光伏出力为0，因此主要靠电网购电和燃气轮机发电供电。

在未来阶段，考虑到光伏单位装机成本会不断下降[12]，因此分析了光伏成本对于最优规划方案的影响，具体结果如表3。

分析表3可知，随着光伏装机成本的下降，所对应的最优规划方案中的PV装机量逐渐增加，而相对应的用户满意度逐渐下降，即光伏装机成本并不能改善用户满意度。

5 结论

针对冷热电联供系统中一次能源消耗过大的问题，本文提出了CCHP系统中光伏容量的优化配置方法。首先介绍了光伏出力和CCHP系统模型，建立了以PV改造收益最大和用户满意度最高为目标的多目标规划模型，提出了基于小生境和模糊理想决策的求解方法，并通过算例进行了有效性验证。算例结果表明，所提出的光伏配置方法可以有效平衡经济收益和用户对于PV接入的满意度。后续研究中，可以考虑增加CCHP系统中的元件类型，考虑电制冷机和储能等装置对于规划结果的影响。

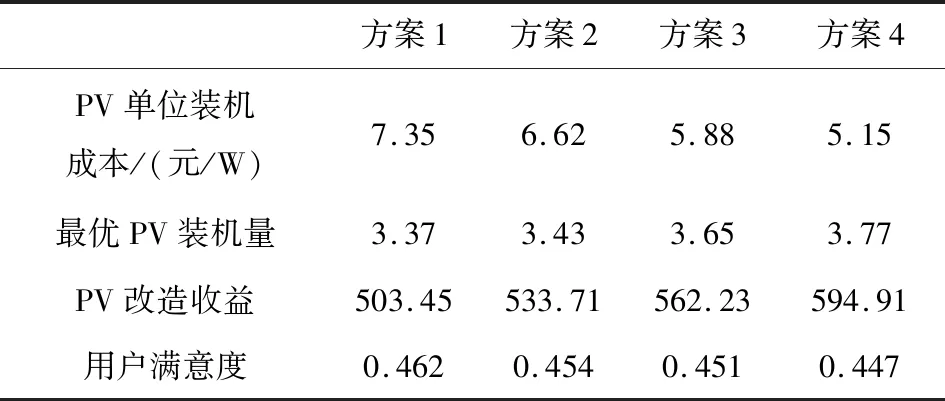
表3 光伏装机成本对于最优规划方案影响分析Tab.3 Impact analysis of PV installation cost on optimal planning scheme