基于时间序列的轨迹数据相似性度量方法研究及应用综述
2020-01-01郭景峰刘风阳
潘 晓,马 昂,郭景峰,吴 雷,2,刘风阳
(1.石家庄铁道大学 经济管理学院,石家庄 050043;2.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;3.天津师范大学 软件学院,天津 300387)
0 引言
在无线通信技术、全球定位技术和智能移动终端高速发展的背景下,无时无刻不在产生时空数据。随着位置信息的积累,形成了TB甚至PB规模的轨迹大数据。过去轨迹数据的构成通常只包括时间和空间信息,可称之为原始轨迹。如今,随着社交媒体的普及和流行(例如,微博、微信等)地理位置与文本数据的融合变得越来越普遍,轨迹数据中蕴含的信息更加丰富。轨迹数据在交通、物流、应急疏散管理、动物迁移等诸多方面有着重要的应用。
轨迹相似性度量的研究是轨迹数据管理和挖掘的基础,在轨迹计算的各个领域发挥着重要作用。例如,在交通管理领域,通过相似性度量可以发现轨迹集中区域,推断交通拥堵情况,提早进行交通疏导[1-3];在城市规划领域,通过发现人类活动的相似性,可以推断城市的功能模块,为城市发展提供帮助[4];在智能推荐领域,通过寻找满足一定时空约束的相似性活动轨迹,可以为用户进行推荐,提高用户体验和用户黏度[5-8];在智慧出行领域,通过借鉴用户相似轨迹,可以合理规划用户出行时间,为智慧出行提供可能[9];在环境空气预测领域,通过与空气的历史轨迹数据进行比较,结合气象、交通流等信息,可预测各区域地区的空气质量[10-11],为环境保护提供助力。
1 轨迹大数据特点
据滴滴工作的最新数据,滴滴出行每天新产生的数据量为70 TB+,每天要处理的轨迹数据量可达4 500 TB。2017年交通运输行业发展统计公报表明,至2017年末全国拥有公路营运汽车1 450.22万辆。国家工信部称截止至2018年5月我国移动电话用户总数近15亿。《可穿戴设备研究报告》报告显示,到2018年,成熟市场中每位消费者将拥有3件以上智能穿戴设备。海量的位置信息为轨迹数据的采集、存储和计算带来巨大挑战。轨迹大数据除具有大数据传统的“4V”特点外,还具有以下特点。
1) 高维异构
轨迹数据中的位置本就属于二维数据。由于位置采样策略和频率的不同,原始轨迹本身就具有数据异构的特点。许多研究者开展了针对轨迹等长、位置对齐等相关工作的研究。最近,伴随着移动社交网络(如Facebook、Twitter、微博等)的流行,原始轨迹中进一步融入了社交图、图片、音频、视频等多元数据,致使轨迹数据的维度剧增。在轨迹大数据上进行相关处理时,需要同时兼顾动态的空间、时间、文本、社交关系等,这并不是一项平凡的任务。此外,随着时间的推移,轨迹数据持续增加,这为在轨迹上的查询处理和挖掘带来巨大挑战。
2) 多粒度
轨迹大数据上的信息具有多粒度的特点。单就位置而言,位置可以分别用离散点、线段、整条轨迹表示。单就一个位置点包含的语义而言,语义本身又体现着层次性。例如,用户的位置是中国人民大学的经纬度,中国人民大学又隶属于高等院校,是教育机构之一。位置与蕴含的语义信息的结合,加剧了轨迹的多粒度特性。具体来讲,每一个特定的语义层次都可以评价单点、轨迹片段、片段集合、乃至整条轨迹。因此,在轨迹上进行相似性度量计算时,如何衡量轨迹上不同信息的粒度、如何支持全粒度(即局部和全局)搜索是一项具有挑战性的工作。
3) 不确定
轨迹的不确定性表现在位置和语义两个方面。受定位设备自身限制、轨迹采样频率的限制,存在采样点丢失或采样频率不均匀等问题,位置采样点和采样点间的推理位置均具有不确定的特点。同时,与轨迹关联的语义,受上下文环境或人为因素的影响,也具有明显的不确定性,如用户的评价回复中存在手工录入的错误信息、同语义的感兴趣点对应不同物理位置的分店等。有时数据的不确定性是由人为故意为之,例如在数据输入阶段,当出现用户不想要公开的信息时,会选择输入一些错误的值或输入替代符号(如*)。数据的不确定性为轨迹相似性的精确计算带来挑战。
4) 高冗余
轨迹中的位置和语义均具有高冗余的特点。位置方面,由于传感器设备以及GPS设备在固定的时间间隔记录数据,并未考虑数据的代表性,所以会造成位置数据冗余。例如,车载GPS在车辆状态没有发生变化的情况下,仍然不停地记录着车辆的当前位置数据。语义信息的冗余更加明显,如关键字单复数重复记录问题、词语的同语义问题等。例如,公开数据集Foursquare[12-13]在兴趣点(Points of Interested, POI)的标注中会同时出现名词的单数和复数形式。再如,堵车、阻塞、等待时间长均表示交通拥堵,只是关键字不同而已。数据的高冗余性为轨迹存储、轨迹相似性的计算带来挑战。
至今,在数据库、数据挖掘、地理信息系统等领域,围绕轨迹相似性度量,已发表了大量的研究工作。本文对现有工作进行总结归纳,第2章对轨迹的形式化表示和相似性度量问题进行了定义,第3章对轨迹相似性度量技术进行了分类,并针对每一种类型总结了相应的特点。第4章梳理了轨迹相似性计算的几个典型应用领域。第5章对未来的研究方向进行展望。最后,对文章进行了总结。
2 问题描述
轨迹大数据上的相似性度量需要同时考虑时间、空间以及语义三方面信息的相似性。空间与时间相似性较直观。语义信息包括文字、图片、语音、视频等,然而无论哪一种形式都可以将其抽象为关键字集合的形式。因此,简单起见,在后续的描述中语义信息均以关键字集合进行代替。
2.1 轨迹表示法
轨迹的表示形式有很多种,主要分为三类:时间序列表示法、图表示法和矩阵表示法。
2.1.1时间序列表示法
一条轨迹t可以表示成为按时间点排列的序列,形式化表示为t={p1,p2,…,pn},其中,对于任意点pi=(l,c,w).pil表示该点所在经纬度,pic表示该对象在此位置的时刻pi.w表示与位置pil相关的语义信息,用文本集合表示。时间序列表示法是轨迹最常用的表示方法之一。例如,用户某天的签到轨迹t1={((116.32, 39.97), 8:00, {Hotel, Sandwich}), ((116.37, 39.96), 12:00, {Gym, pizza}), ((116.37, 39.95), 15:00, {Mall, Coffee}), ((116.44, 39.95), 21:00, {Cinema}), ((135.44, 39.95), 23:00, {Bar})}。本文主要研究用时间序列表示的轨迹。
2.1.2轨迹其他表示法
图表示法:轨迹集合亦可以用图形式化地表示。设G=
矩阵表示法:轨迹还可以用高维矩阵表示,如图2所示,图2中间位置的矩阵是将轨迹转化为一个用户—位置矩阵。矩阵的每一行代表一个用户,矩阵的每一列表示签到点的位置,如经纬度,矩阵中的每一个元素代表用户对某个位置的访问次数或访问持续时间等。图2右侧矩阵是将轨迹转化为一个位置—活动矩阵。矩阵的每一行代表一个点的位置,矩阵的每一列表示用户在签到点的活动,如购物等,矩阵中的每一个元素代表在用户是否在该个位置进行某项活动或活动的频率。
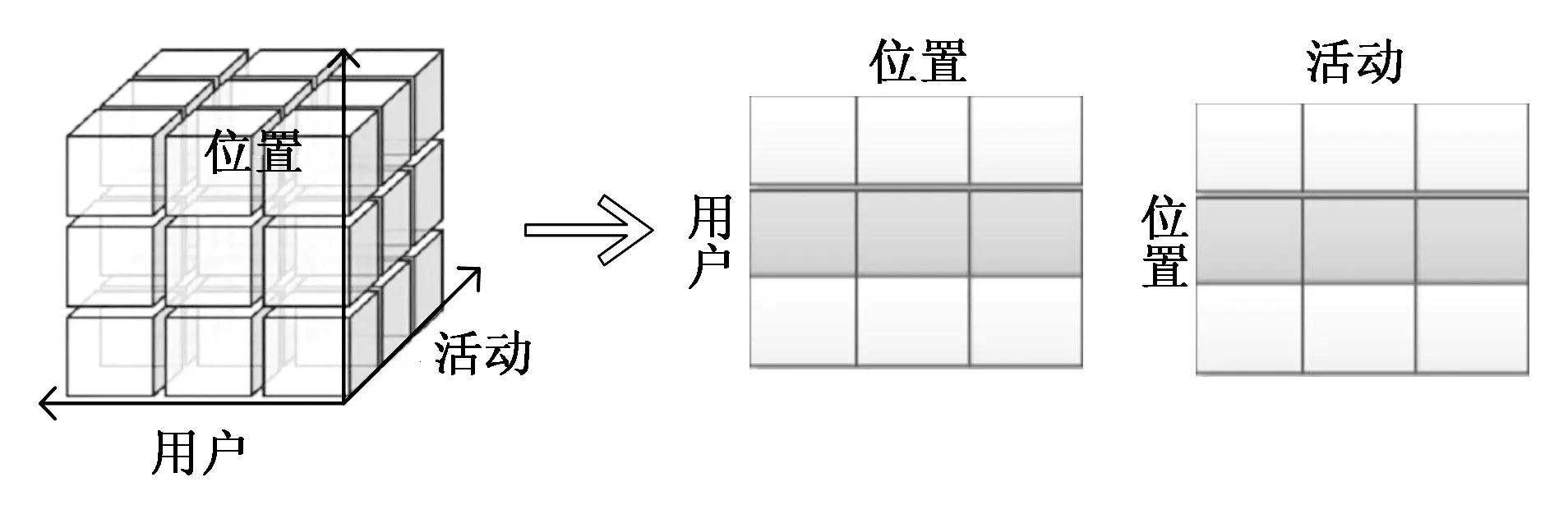
图2 轨迹的矩阵表示法Fig.2 Matrix representation of trajectories
2.2 轨迹相似性表示
定义1(轨迹相似性)设向量ω=(ω1,ω2,ω3)为轨迹相似性权重向量,其中ωi(i=1,2,3)分别表示空间、时间、文本的相似性权重,ω1+ω2+ω3=1。给定任意两条轨迹t1,t2,则轨迹t1,t2的相似性可用向量点积表示

(1)
其中,d1(·),d2(·),d3(·)分别表示两条轨迹在空间,时间,文本的距离函数。利用点到点的距离(记为distk(·))并将其归一化,可以求得轨迹与轨迹的距离
(2)
当ω取不同值时,代表不同的轨迹相似性。例如,当ω是仅有一个元素为1的单位向量时,分别代表轨迹的空间相似性、时间相似性和文本相似性。现有工作[14-26]中有关ω的不同取值总结如表1所示。

表1 ω与轨迹相似性度量范围的关系Tab.1 The relationship between ω and trajectorysimilarity measure range
定义1中的轨迹相似性定义对噪音敏感,可以采用设定阈值的方法解决对噪音敏感的问题[5-6,22,26-27]。
定义2(基于阈值的轨迹相似性)设θ={θ1,θ2,θ3}为距离约束阈值集合,其中θi(i= 1,2,3)分别表示空间、时间、文本的距离阈值。对于轨迹t1,t2上任意两点p1,i,p2,j,修订点到点的距离distk(p1,i,p2,j)如式(3)或式(4)所示,
(3)
(4)
式(3),式(4)通过设定约束阈值集合θ,可以过滤超过阈值的噪音。当然,对于噪音的清洗还有很多其他的方法,如针对可接受噪音可用地图匹配(Map Matching)算法予以纠正,针对不可接受噪音可以用均值过滤(Mean Filter)法或卡尔曼与粒子滤波过滤(Kalman and Particle Filters)法用估计值替代,也可用基于启发式规则的异常点检测(Heuristics-Based Outlier Detection)法直接去噪,具体可参见文献[28],本文不一一赘述。
3 轨迹相似性度量方法
轨迹相似性受很多因素影响,例如,轨迹长度、形状、运动趋势、时间约束等。轨迹相似性度量分类方法很多,下面分别从数据类型、轨迹形式和度量范围几个方面对现有工作进行总结。
3.1 面向不同数据类型的相似性度量方法
从轨迹包含的数据类型的角度,相似性可从空间、时间、文本三个方面度量。
3.1.1空间相似性
空间相似性[14-16]是指从空间位置角度,若两条轨迹距离很近或者轨迹形状相似,则认为两条轨迹相似。本文将定义轨迹与轨迹空间相似性的度量方法分为常用空间度量方法、基于时间序列的度量方法和基于编辑距离及其扩展的度量方法三种。表2展示了各典型方法在噪音敏感、时间约束和轨迹是否要求等长等方面的比较。

表2 轨迹空间距离函数Tab.2 Trajectory space distance function
1) 常用空间距离度量方法
Lp-norm距离:该方法是计算位置距离最常用的方法,形式化表示为
(5)
式中,x的不同取值代表了不同的距离函数,如表3所示。现有轨迹相似性度量大多基于欧氏距离[5-6,20,26,29-33]。Lp-norm距离的缺点是不能处理局部时间偏移,局部时移是指在对齐两条轨迹时容忍短期差异(例如,样本点缺失,测量误差等)的能力。

表3 x的取值与Lp-normTab.3 x and Lp-norm
Hausdorff距离:Hausdorff距离由Felix Hausdorff提出,原本用来度量空间中的两个位置点集合的距离。将其应用在轨迹中,直观上来讲,是将轨迹上最近点距离的最大值作为轨迹空间距离,具体公式为
dH(t1,t2)=max(h(t1,t2),h(t2,t1)),
(6)
(7)
其中,dH(t1,t2)为双向对称距离,h(t1,t2)为单向非对称距离,‖p1,i-p2,j‖为两点之间的空间距离。文献[15]在道路网络中利用Hausdorff距离计算轨迹空间相似性。如图3所示,对于轨迹t1上的每一个点,依次计算该点到轨迹t2上所有点距离中的最小值,然后针对轨迹t1上的所有点,求最小值中的最大值即h(t1,t2)=3。同理可计算h(t2,t1)=4。所以,dH(t1,t2)=max(3,4)=4。由于Hausdorff距离是基于集合定义的,因此,将其应用于轨迹时,位置上的时间信息被忽略了。
图3 Hausdorff距离在路网中的应用Fig.3 Application of Hausdorff distance in road network
片段距离:考虑到度量整条轨迹不能很好地表示轨迹间的相似性,可用轨迹中具有代表性的轨迹片段来评价轨迹相似性。文献[19]将轨迹划分成了若干片段,通过衡量轨迹片段的相似性评价两条轨迹的空间相似性,如图4所示。为了便于区别,轨迹线段记为Li。文献[19]通过计算轨迹片段的垂直距离(式(8)),平行距离(式(9))以及角度距离(式(10)),并将三者加权求和(式(11)),得出两条轨迹片段的距离。然而,该方法仅考虑了轨迹形状的相似程度,忽略了位置上的时间因素。

图4 轨迹线段表示Fig.4 Line segment representation of trajectory
(8)
dl(Li,Lj)=min(Ll1,Ll2),
(9)
(10)
dLS(Li,Lj)=ωνdν(Li,Lj)+ωldl(Li,Lj)+
ωθdθ(Li,Lj)。
(11)
Fréchet距离:Fréchet距离[34]是法国数学家Maurice René Fréchet在1906年提出的一种路径空间相似性描述,也称为狗绳距离,如图5所示。主人按路径t1行走,狗按路径t2行走,各自完成这两条路径的过程中需要的最短狗绳长度即直观意义上的Fréchet距离。设t1和t2是两条轨迹,α和β是两个重参数化函数,c为时间,则轨迹t1与轨迹t2的Fréchet距离dF(t1,t2)定义为
dF(t1,t2)=
(12)
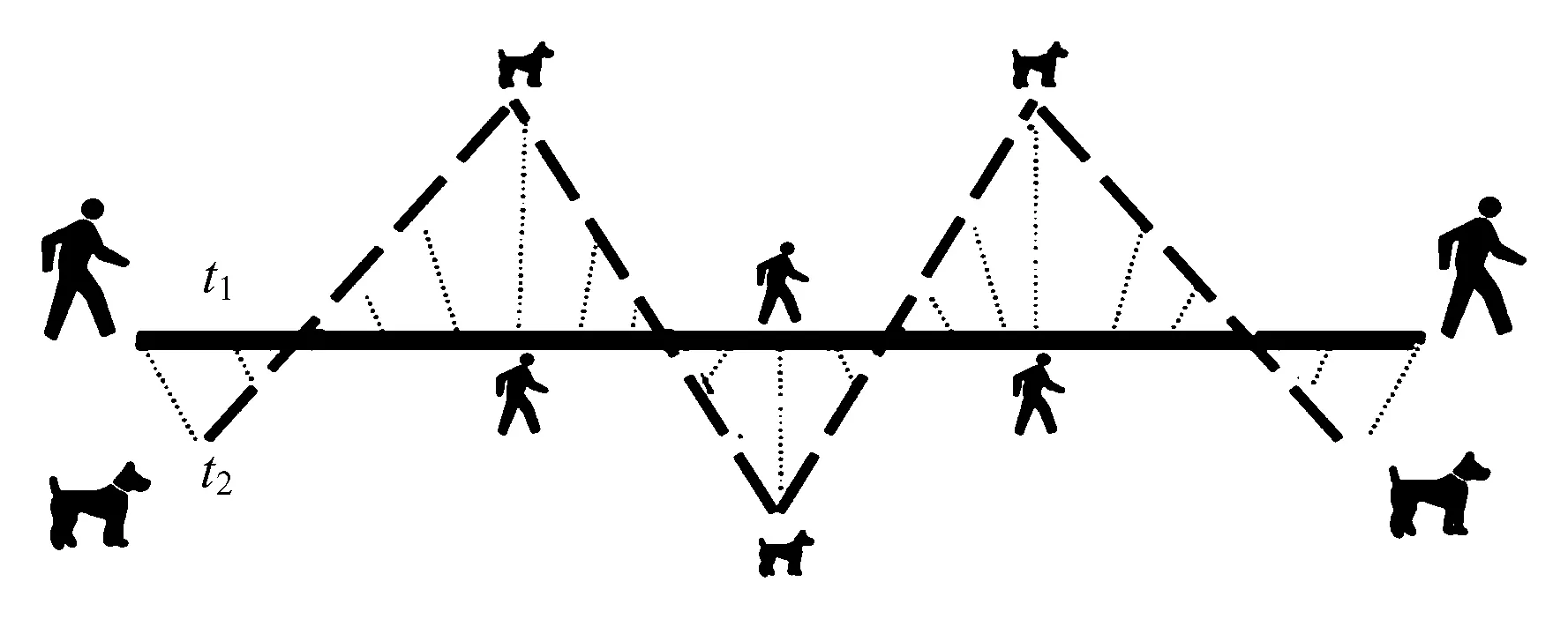
图5 Fréchet距离Fig.5 Fréchet Distance
OWD距离:文献[35]从轨迹空间形状出发,提出了一种新的空间距离计算方法OWD(One Way Distance)距离。该方法将一条轨迹t1看作离散点的集合,另一个轨迹t2看作连续的线段集合(用分段函数表示)。OWD是轨迹t1上的所有点到轨迹t2所有线段的距离平均值作为两条轨迹空间相似距离,具体公式为

(13)
TS-Join距离:文献[36]考虑到轨迹的相似性与轨迹距离并不是呈线性递增的特点,运用指数函数更好地度量了轨迹间的相似性。点到轨迹的距离定义为点到轨迹上所有点的距离的最小值,具体公式为
(14)
则轨迹与轨迹的相似性为
2) 基于时间序列的度量方法
动态时间规划及其扩展:DTW大概在1970年左右被提出。DTW通过把时间序列进行延伸和缩短,计算两个时间序列之间的相似性。由于轨迹数据可以看成是在多维空间中的时间序列,因此,可以采用DTW定义轨迹间的相似度。给定轨迹t1={p1,1,p1,2,…,p1,n} ,设Hd(t1)=p1,1,R(t1)={p1,2,…,p1,n},t2={p2,1,p2,2,…,p2,n}则轨迹t1和t2的DTW距离为
(16)
式中,函数dist1(·)为距离函数可采用曼哈顿距离、欧式距离等。DTW解决了轨迹采样频率不同的问题,但对噪音较为敏感。PDTW[37]在DTW基础上进行改进,利用轨迹简化率将轨迹简化,在简化后的轨迹上套用DTW,求解轨迹间距离,提高了DTW的算法效率,其计算原理与DTW相同。
最长公共子序列:轨迹中的噪音可能导致轨迹局部距离过大。为了解决相似性计算对噪音敏感的问题,文献[38]提出利用最长公共子序列定义两条轨迹的空间距离。设轨迹t1={p1,1,p1,2,…,p1,n},t2={p2,1,p2,2,…,p2,n},则轨迹t1和t2的LCSS距离定义为
(17)
式中,参数δ用于控制两条轨迹的长度。θ1是一个距离阈值,用以判断某点是否用于计算LCSS距离。若两点间的距离小于阈值θ1,则将两者距离记为1;否则忽略。LCSS距离的本质是统计在一定范围内轨迹上距离较近的匹配点数量。LCSS距离虽然可防止噪音干扰,但两个阈值δ和θ1较难确定。因此,有可能误将两条不相似的轨迹定义为相似轨迹。
同步欧几里得距离:文献[39]将轨迹的每一条线段看成一个关于时间u的线性函数t1(u),计算移动物体1在c时刻的位置。利用此线性函数可计算每一个时刻轨迹上对应点对的欧式距离。如此,将所有同步的欧式距离积分再除以两条轨迹总的时间,即是两条轨迹的距离,
3) 编辑距离及其扩展
基于序列的编辑距离:文献[40]扩展了在字符串上的编辑距离定义,提出了一个新的距离函数—基于序列的编辑距离(EDR距离),如式(19)所示。与LCSS关注寻找轨迹的相同点不同,EDR距离更关心的是两条轨迹的不同点。直观上,EDR是两条轨迹上一个位置转成另一个位置的代价和。该代价是将一个位置转成另一个位置所需的编辑操作次数,编辑操作包括插入、删除和替代。如图6所示,实心点表示原有轨迹上的点,空心点表示插入或替代的点。如果两个位置间的距离大于阈值则进行插入或替代操作,如图6中的p1″,p2″,p5″。需要说明的是,EDR考虑了由于轨迹长度不同对轨迹相似性所造成的影响,最终得出的是编辑操作的次数,但并不是具体的空间距离值。式(19)中若t1和t2轨迹对应两点间距离小于阈值,则c值为0;反之,c值为1。
(19)
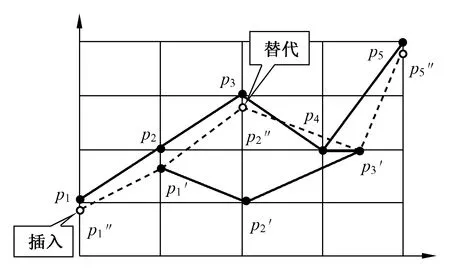
图6 EDR距离Fig.6 EDR distance
ERP距离:文献[41]提出一种称为ERP(Edit distance with Real Penalty)的度量方法,该方法既满足三角不等式,又能处理局部时间偏移。设轨迹t1与t2的长度分别为n和m(n≥m),二者间的ERP距离定义为
(20)
ERP距离通过为轨迹添加间隙点(即零点)解决轨迹对齐问题。间隙点选取位置以使轨迹的ERP距离最小为原则。若p2,j和p1,i均不是间隙点,则dist(p2,j,p1,i)为这点间实际距离;若两点中有一个为间隙点,则 为间隙点与另一个非间隙点的距离。
ERP使用了参考点g计算不匹配点的距离,而不像LCSS将这个距离设置为0,因此它满足三角不等式的约束。
基于线段的编辑距离:文献[14]基于EDR方法提出一种在轨迹线段上的编辑距离空间相似性计算方法EDS(Edit Distance on Segment)。首先将轨迹划分成若干轨迹片段,两个轨迹之间的距离定义为子轨迹转换的最小代价,包括替代代价、拉伸代价和旋转代价,即C(r,r′)。两条轨迹的空间相似性距离为
(21)
por(L1·r1,L2·r2)为用轨迹片段L2·r1替代L1·r1的部分,L1L1·r1为轨迹L1除去r1后剩余轨迹。
3.1.2文本相似性
文本相似性主要用以评价轨迹数据上所标注的文本信息的相似程度。在轨迹上文本信息标注的粒度由粗到细分别为整条轨迹、线段及线段集合和单位置点。无论哪一种粒度,其文本相似性的评价方法主要包括TF-IDF[17-19]、Jaccard距离[22]、编辑距离[23]、余弦相似性、SimHash+汉明距离和语言模型。
1) TF-IDF
TF-IDF的主要思想是,如果某个词或短语,(记为A),在一篇文档中(记为B)出现的频率dTF高,并且在其他文档中很少出现,则认为此词或者短语具有很好的类别区分能力。TF-IDF具体的计算公式为
dTF-IDF=dTF·dIDF,
(22)
式中,dTF为词频(Term Frequency),dIDF为反文档频率(Inverse Document Frequency),该方法综合考虑了词的频率和词的文档频率,
(23)
(24)
在轨迹中应用该模型时,文档对应于一条轨迹上所有的文本信息集合,语料库即所有轨迹上的文本信息的值域。
2) Jaccard距离
Jaccard系数用于比较文本集之间的相似性与差异性。Jaccard系数值越大,文本相似度越高。
(25)
式中,t1·w表示第1条轨迹所含的全部文本信息的集合。
Jaccard距离与Jaccard系数相关,Jaccard距离越大,文本集合相似度越低,
dJD(t1·w,t2·w)=1-J(t1·w,t2·w)。
(26)
3) 编辑距离
编辑距离(Edit Distance),又称Levenshtein距离,是指两个字串之间,由一个串转成另一个串所需的最少编辑操作次数。编辑操作包括替换、插入和删除。一般来说,编辑距离越小,两个串的相似度越大。两个字符串s1,s2的编辑距离定义为
(27)
式中,dEdit(s1,i,s2,j)表示s1字符串中长度为i的子串到s2字符串中长度为j的子串的编辑距离。
4) 余弦相似性
直观的,如果两句话中用词越相似,则其内容就越相似。因此,余弦相似性从词频入手,计算文本的相似程度。首先,统计文本信息中蕴含词的词频。例如,I am a girl和I am a boy,其中单词有I、am、a、girl、boy。第一个句子中的词频向量为(1,1,1,1,0),第二个句子中的词频向量为(1,1,1,0,1)。然后,文本的相似度可以通过向量夹角表示。夹角越小代表两个句子越相似。数学家已经证明,余弦的这种计算方法对n维向量也成立,计算公式为
(28)
5) SimHash+汉明距离
SimHash是谷歌发明的算法,可以将一个文档或字符串通过Hash算法转换成64位的字节。通过判断两个字节的汉明距离计算字符串相似性。与编辑距离不同,汉明距离是计算两个等长字符串相同位置不同字符的个数,如式(29)所示,其中⊕表示异或,
dSH(p1·w,p2·w)=∑p1·w[i]⊕p2·w[i]。
(29)
例如,两个对象p1·w=“toned”,p2·w=“roses”。p1·w与p2·w的汉明距离dSH(p1·w,p2·w)=3。
6) 统计语言模型
统计语言模型被广泛应用于各种自然语言处理问题,如语音识别、机器翻译、分词、词性标注等。Okapi BM25 是一种文献匹配度评分模型。Okapi BM25考虑到既使两个相同主题的文档其关键词频率和文档长度不一定相同,因此在TF-IDF 的基础上改进,增加了两个可调参数(k和b),分别代表词语频率饱和度(term frequency saturation)和字段长度规约,使得文本相似性更加公平客观。轨迹t1和t2的文本相似性计算公式为
(30)
f(p1,i·w,t2·w)为p1,i中的关键字在t2轨迹关键字集合中出现的频率,avg表示所有轨迹包含关键字个数的均值。
3.1.3时间相似性
就时间表示粒度而言,时间可以用精确的时刻,也可用时段进行表示。当用时刻表示时,判断时间相似性有两种方法:第一,仅比较两时刻是否一致,如果一致则认为相似,反之亦然,见式(31)。显然,该方法过于严苛。第二种方法是为时间相似性设定某个阈值,如果两时刻的时间差在阈值范围内,则认为相似,如果超出某个阈值则认为不相似,见式(32)。当时间是一个时段时,可以通过衡量两区间是否相似来衡量时间的相似性。具体来讲,两个区间相似性可以定义为两时段的相交区域与两个时段的并的比值,见式(33),该比值越大说明时间相似性越高。
(31)
(32)
d2(p1,i·c,p2,j·c)=
(33)
轨迹时间标注的粒度与文本类似,由细到粗亦可分为单点位置、轨迹线段、整条轨迹。如果时间标注粒度为单点位置,根据时间的不同表示形式可以采用式(31)~(32)计算相应的时间相似性。如果时间粒度为轨迹线段或整条轨迹,根据时间的不同表示形式可分为:如果线段端点用时刻表示,可采用式(32)计算相应的时间相似性;如果线段端点用区间表示,可采用式(33)计算时间相似性;如果整条线段采用区间表示,也可以采用式(33)计算时间相似性。
3.2 面向不同轨迹形式及度量范围的相似性度量方法
从前面的描述可知,轨迹具有两种形式:离散点和轨迹片段。整条轨迹可作为轨迹片段的特例。根据评价相似轨迹的粒度不同,可以将相似性度量范围分为局部相似性和全局相似性。局部相似性是从整条轨迹中寻找满足相似性要求的轨迹片段或片段集合;全局相似性旨在寻找满足相似性要求的整条轨迹。综合轨迹形式与度量范围,可以将现有工作分为4类,离散点+全局相似性、离散点+局部相似性、片段+全局相似性、片段+局部相似性。目前,大部分工作主要集中于全局相似性研究上。
1) 基于离散点的轨迹全局相似性
基于离散点的轨迹全局相似性即通过计算轨迹上的离散点的相似性返回满足要求的整条轨迹。此类工作大部分是通过单独计算轨迹在时间、空间、文本三类数据的相似度距离,通过设定不同的权重,求得单方面或综合两两组合的相似性距离的加权平均值。针对轨迹空间单方面相似性的研究存在大量工作[15,16,34,42-50]。文献[22]和文献[24]针对空间、文本两种数据类型定义相似性,文献[26]是针对轨迹时间、空间、文本三类数据的加权平均。文献[22,24,26]主要针对在自由空间的空间数据。文献[15]利用Hausdorff距离求解在道路网络中的轨迹相似性。
2) 基于离散点的轨迹局部相似性
基于离散点的轨迹局部相似性即通过计算轨迹上离散点的时空和文本相似性,返回满足要求的轨迹片段。若两条轨迹的子轨迹间距离小于给定阈值,则认为这两个子轨迹是相似的。文献[23]利用编辑距离计算文本相关性,利用轨迹长度(即轨迹上相邻两个位置点的距离和)作为空间距离,并用sigmoid函数归一化。通过对空间和文本加权求和计算相似性,返回满足相似性要求的轨迹片段。文献[21]针对轨迹空间,时间两种数据类型定义轨迹相似度,提出了一种基于时间约束的Hausdorff距离时空轨迹相似性计算方法,该方法利用滑动窗口找到两条较长轨迹中所有相似的子轨迹,从而判断出较长轨迹间的相似性。
3) 基于线段的轨迹相似性
基于线段的轨迹相似性可以分为全局相似与局部相似两类。无论是全局相似性还是局部相似性,其计算方法本质相同,均将线段作为计算的基本单元,只是返回的轨迹形式不同。全局相似性返回整条轨迹,而局部相似性返回轨迹片段或片段集合。
基于轨迹线段的轨迹全局相似性通过计算整条轨迹是否满足事先设定的相似性阈值,判断两条轨迹的相似性。文献[14]将轨迹划分成若干轨迹片段,定义两个轨迹之间的距离为子轨迹转换的最小代价,包括替代代价、拉伸代价和旋转代价三者加权和,返回包含与查询轨迹相似的部分的整条轨迹。文献[16,32]同样将轨迹划分为若干轨迹片段,将轨迹线段的相似性定义为轨迹线段的垂直距离,水平距离以及角度距离三方面加权和,将这三个距离整合为轨迹线段间的距离,距离越小则轨迹线段相似度越大,返回与查询轨迹相似的轨迹线段。
不同轨迹相似性度量方法的对比如表4所示。
4 应用场景
轨迹相似性度量作为轨迹数据分析与挖掘的基础,在各个领域具有十分重要的意义。
4.1 交通管理
城市交通管理一直都是各个国家为之困扰的问题。随着经济贸易和社会活动日益繁忙,城市交通以前所未有的速度迅速增长,交通管理问题也日益严重。我国城市特别是大城市,在交通拥堵、车道违法占用、不安全驾驶行为等方面存在严重的交通安全隐患。

表4 轨迹相似性度量方法比较Tab.4 Comparison of trajectory similarity measurement methods
现在,大多数公共交通以及私家车都安装有GPS,通过对车载GPS模块采集的车辆轨迹数据进行相似性分析,可以发现城市中车辆在一定时间范围内容易集中的区域,对这些区域提早进行交通疏导管理,从根源上排除安全隐患。文献[43]先定义了轨迹间距离,通过基于密度聚类算法对历史轨迹进行聚类,推测用户目的地。该项研究有助于避免人流聚集,防范重大交通事故和灾难性城市安全事件,避免类似上海外滩事件的事件发生。
文献[1-2]分别通过对出租车轨迹进行空间和时间相似性分析,实现检测大规模轨迹流中的异常对象。例如,文献[1]通过判断在一定时间阈值下轨迹所含相邻轨迹的个数来判断轨迹是否相似。若司机不停地改变车道,则该司机将可能被归类为异常对象。文献[2]通过分析整条轨迹序列的时间是否大于给定阈值来判断轨迹是否为异常轨迹。该研究有助于检测超速驾驶、酒后驾车等其他异常行为,为交通管理部门评价和管理驾驶员的驾驶行为提供科学的依据。
4.2 城市规划
城市化与现代文明的发展使得城市在发展中形成了不同的功能区域,如住宅区、商业区、教育区等。这些功能区域可以根据人们的生活方式自然形成,也可以由规划师人为设计。随着时间的推移,功能区域亦会随着城市发展不断变化。功能区域的识别可为城市规划、商业布局选址等多方面提供帮助。
文献[4]利用移动轨迹相似性分析找到所蕴含的相似移动行为模式。通过相同行为模式推导出城市区域属性。例如,如果大多数轨迹在深夜访问某个区域,则该区域很有可能为住宅区,如果大多数轨迹在工作日的上班时间段聚集,则该区域很可能为公司或教育区等等,图7显示的是文献[4]对北京市功能区域的识别,不同深浅度代表不同的功能区域。

图7 城市区域标记Fig.7 City area marker
文献[46]通过对出租车轨迹的相似性分析,发现不同时间段居民出行的热点路径和出租车上下客热点区域,获取其隐含的出行行为规律信息,为城市区域设置和城市路线规划问题的解决提供新途径。
4.3 智能推荐
智能推荐是通过数据挖掘、人工智能等技术,为用户推荐更优化的服务。海量轨迹数据中除了位置和时间外,还包括丰富的语义信息,如兴趣点类型、地理环境、用户评价、道路状况、天气条件、邻近朋友等数据。丰富的数据和信息为学习用户习惯、用户行为模式提供了强有力的数据支撑,为基于位置的推荐服务研究提供了助力。
文献[33]从包含空间及文本信息的轨迹中利用kNN方法,找到与用户查询轨迹空间、文本方面均满足的k条轨迹,并将其推荐给用户。基于用户轨迹或行为相似则偏好可能相似这一观察,文献[6]利用基于密度的聚类方法,从轨迹中发现移动对象密集区域,学习其中的共同行为模式并识别在一定时间段内聚集的移动物体,这些聚集能够为智能推荐提供推荐依据。文献[7]利用核密度估计模型以及加权snippet shift方法从轨迹中发现相同高频的移动行为模式,如图8所示,例如,办公-饭店-办公-小区模式。文献[8]通过一种潜在的基于主题的聚类算法,针对轨迹的语义层面识别出频繁语义区域,通过条件概率模型得到区域间的转换概率,学习其中的共同行为模式。文献[3]使用带有优化聚类的MapReduce编程模型来挖掘Coterie模式,即要求在不等时间间隔约束下找出具有相似轨迹行为的模式,并提出基于语义的距离敏感推荐策略和基于语义的从众性推荐策略。

图8 相似行为模式Fig.8 Similar behavior model
4.4 智慧出行
出行是人类生活必不可少的一部分,在私家车泛滥的年代,合理规划出行显得更加重要。智慧出行是指基于大数据利用数据挖掘、人工智能等方法合理规划出行时间、出行费用、出行方式等[50]。用户出行时,可以把今天要去的地方以及时间罗列出来,通过对历史轨迹数据的相似性分析,结合其他数据源如实时的天气数据,得出与用户需求相近的轨迹数据,用户可以以这些数据为参考合理安排空闲时间。
文献[9]设计实现了一个实时拼车系统,如图9所示,在9(a)中,蓝色轨迹为某车辆规划轨迹,当出现一个新的用户需求时(如9(a)中红色虚线部分),该车辆会及时调整路线规划,调整后规划路线如图9(b)所示,图9(c)为行程完成后的界面。该系统可以找到有相似出行需求的用户,在不耽误用户到达时间的前提下为用户节约资金,用户可以自行设定节约资金与延长时间的比例,使得用户不被频繁打扰。
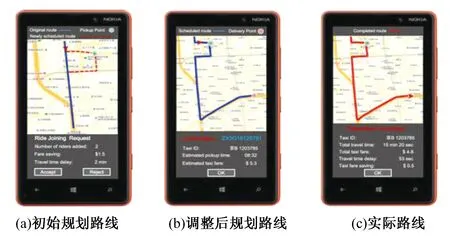
图9 实时拼车系统T-ShareFig.9 Real-time car sharing system T-Share
4.5 环境保护
近年来随着PM2.5、PM10等问题日益严重,环境质量预测及污染物检测受到广泛关注。气象预测和空气质量预测是通过已取得的情报资料和监测统计数据,对未来或未知的环境进行估计和推测,对控制污染保护环境和人们身体健康有着非常重要的意义。
许多城市都有自己的天气检测系统,和地面空气监测站一起实时感知气象数据和地面的空气质量。然而,由于监测站等设备和仪器的建设和维护成本很高,一个城市通常也仅有有限个站点,例如,偌大的北京市只有22个空气监测站,这些站点并不能完全覆盖整个城市范围[10]。同时,气候和空气质量的变化受很多因素影响(如,交通流量、气象条件等)。即使空间距离很近的监测站得出的数据信息也会存在显著差异。
文献[10]利用历史天气质量轨迹数据,提出了一种基于由两个独立的分类器组成的协同训练框架的半监督学习方法。利用人工神经网络(ANN)和条件随机场(CRF),分别针对时间相关特征(例如,交通和气象)以及位置相关特征(例如,道路长度和兴趣点类别)进行建模,结合天气、交通流量、路网和兴趣点等多种数据源,预测各区域的空气质量信息。
5 研究趋势展望
5.1 技术方面
1) 可调节匹配度的相似轨迹研究
现有大部分工作研究的是严格(强)相似性定义下的全局相似轨迹。具体来说,在计算轨迹相似性时,寻找的相似轨迹需要同时满足时空约束与文本约束,同时这些约束是集中在相同对象上的。如图10中的两条轨迹,在强相似性要求的定义下,两轨迹是不匹配的。因为轨迹上没有一个点与另一个轨迹上的任意一点满足时间、空间和文本一致性要求。然而,这两条轨迹符合弱匹配的要求,即允许满足时空相似性的点与满足文本相似性的点不是同一个点。

图10 弱匹配度举例Fig.10 An example for weak match
研究具有弱匹配度的相似性轨迹是有意义的。例如,在为签到用户推荐签到地址时,只需关注用户签到的地点和顺序,无需严格要求签到时间完全相同。现有在弱匹配度的方面研究较少。实际上,不同的应用场景,轨迹匹配度的要求不一样。研究可调节匹配度、具有自适应特点的轨迹相似性研究仍是一项开放的课题。
2) 约束阈值学习
相似性轨迹的确定需要很多阈值,如空间、文本和时间的权重、相似程度的阈值。现有的大部分工作都是让用户自己定义相关阈值。约束阈值取值的好坏直接影响最终的相似性。如何合理设定这些阈值,使得查询结果更好地满足用户需求,是一个非常有意义的研究问题。目前,机器学习领域的回归模型、分类模型、主成分分析方法、层次分析法等方法可以通过训练样本数据给出更客观和符合规律的权重值,这样得出的权重或阈值比人为设定得出的相似性结果将更客观。
3) 图相似性计算方法
如前所述,轨迹除了使用时间序列表示以外还可以使用图来表示。现有轨迹相似性计算大部分基于时间序列的表示形式[9,26,29,36-37,46,51]。众所周知,在图中具有很多经典的理论和方法。如针对图的分析方法有Deepwalk、Node2Vec、Struc2Vec、RolX核心方法等,可以根据相邻节点和边将结构相同即相似的节点进行分类。目前,这些方法主要用于比较节点的相似性,对于轨迹图的相似性还需进行改进。
4) 高阶张量技术
张量是一个可用来表示矢量、标量和其他张量之间线性关系的多线性函数。正如引言部分所述,轨迹可以由高维矩阵来表示,即高阶张量,则轨迹的相似性还可以通过张量分解等技术来计算,常见的张量分解方法有Basic MF,正则化矩阵分解,CP分解等。当将这些方法应用到高维轨迹数据时,可以进行适当的改进和扩展。
5.2 应用场景
轨迹的概念可以被拓展到很多场景。除了通常认为的位置相关轨迹外,还可以延伸到各个领域,例如,购买轨迹,职业轨迹,健康轨迹等。
1) 购买行为轨迹
中国的网购热潮推动了经济的快速发展,网上购物也已经成为人们生活的重要一部分。人们在这些网站上的行为构成了各种各样的行为轨迹信息。个人在网络上进行购物时,将进行一系列行为,例如,浏览,收藏,加入购物车,购买等。将用户的这些购买行为按照时间进行排序,就形成了用户的购买行为轨迹。用户的购买行为并不是孤立的,相互之间具有联系。通过分析相似客户的购买行为,可以根据用户最近购买、收藏、加入购物车中的物品等推断用户即将购买的产品。此外,对客户的购买行为轨迹进行分析,有助于为用户画像、发现相似用户群体。商家可以利用这些信息为用户进行个性化推荐,提高广告投放价值。
2) 职业轨迹
职业轨迹指将个人的职业经历按时间进行排序形成的轨迹数据。人的一生可能会经历几次职业的转变,每一次职业的转变都会面临着风险。通过对人的职业轨迹进行相似性分析,可以识别拥有相似性就职经历的人群。此外,虽然成功人士的经历不可复制,但是其成功的经验仍具有一定的借鉴意义。通过在若干职业轨迹中查找相似性轨迹,可以帮助人们对今后的就职方向进行决策。文献[25]通过利用经典序列对比方法,研究人与人之间的职业轨迹的相似性,为人们职业规划提供帮助。
3) 健康轨迹
随着智能穿戴设备的普及和流行,智能穿戴设备上记录的信息随着时间的积累将形成用户的健康轨迹,通过对这些轨迹进行分析,可以找到身体状况相似的用户群体。同群体用户的相关经验有助于彼此借鉴,同时对商家来说可提高广告投放的回报率和价值。
5.3 安全与隐私
轨迹数据包含了许多个人敏感信息,对轨迹进行分析必然会带来隐私泄露的风险。文献[52-53]指出连续性的轨迹数据暴露会更容易被攻击者获取其行为习惯或者其日常工作场景。虽然已有一些对用户隐私数据提供保护的方法研究,例如,加密、匿名化、差分等[54-55]。然而,现有方法在解决轨迹数据隐私保护问题上仍需进一步提高。在用户轨迹隐私保护方面仍有很多开放的问题有待进一步讨论研究。
6 结束语
定位技术和基于位置服务应用的蓬勃发展积累了大量的用户时空、文本、图像数据,形成海量轨迹大数据。这些轨迹数据中蕴含了丰富的信息,为交通管理、城市规划、智慧出行、环境保护等提供了重要的帮助。本文通过对现有的轨迹相似性度量工作进行总结归纳,提炼了轨迹大数据的特点以及在轨迹大数据上度量相似性存在的挑战。从不同的数据类型、轨迹形式和度量范围对现有的相似性计算方法进行了归纳总结,并分析了各种方法的优缺点。讨论了轨迹相似性在各个典型领域中的具体应用场景。最后,针对轨迹大数据未来可能的研究方向提出了展望。
