基于分层法功能梯度压电材料单裂纹的受力分析

朱 帅，刘海涛

(河北工业大学 机械工程学院，天津 300130)

0 引言

压电材料是一种各向异性，存在机电耦合性质的特殊介电材料，在变形时会产生电场，在外界电场作用时产生机械变形，其在车辆工程、军工和航天航空等领域有重要的作用，尤其是在传感器、驱动器和控制器[1]中有很广泛的应用。

功能梯度材料[2]是一种本身构成和布局连续变化的材料，材料的力学性质不会发生跳跃性的变化，比如弹性模量、介电常数和压电常数都是以函数的形式，在空间上以一种均匀过渡的方式呈现一种梯度的变化。这种材料较普通材料而言，可以很大程度上缓解结构中应力集中的问题，从而在不同的位置有着不同的力学性质，使整体结构更加改善，不易发生破坏，广泛应用于机械配件、光纤、人造器官、军事等领域。随着科技的进步，功能梯度被引入到压电材料中，功能梯度压电材料的出现可以减缓压电材料应力集中，大大提高压电元件的可靠性和使用寿命。但是由于材料在制造和使用过程中会产生各种裂纹缺陷，从而使材料破坏，功能丧失，因此对于含裂纹的功能梯度压电材料的研究显得尤为重要。

当前功能梯度压电材料的研究方法主要是解析法居多，比如匡震邦和马法尚[3]利用应力函数解法求出了当材料是横观各向同性下，包含椭圆形孔的压电体的解法。程家幸等[4]研究了含微孔洞的功能梯度压电材料矩形板的热屈曲相关特性。孟广伟[5]利用光滑有限元理论分析了含孔功能梯度压电材料的力电耦合行为。Almajid等[6]在层合板理论上，分析了功能梯度压电板的离面位移和应力场。曹志远[7]在特定的几何形状和简单的边界条件下，建立了膜弯耦联的功能梯度壳体的一般性基本方程。杨权权等[8]基于复变函数理论和保角变换技术研究了功能梯度材料加强环孔的应力集中。陈淑萍等[9]引入PLEVAKO解，利用分离变量法，求出了四边简支功能梯度矩形板解析解。Lothe 和Bamett[10]以Stroh的方法研究了在线性力和位错下压电材料的电场以及弹性场的分布情况。由于解析法需要简化很多条件，做较多假设，计算推导过程较复杂，导致解析法一般只可以计算特定的几何形状和载荷下的解析解。

考虑到功能梯度材料的不均匀性，Wang等[11-12]提出了功能梯度压电结构分层模型，利用分层近似处理的方法[13-14]划分为若干层，每层的材料参数按照所取的函数进行设置，在界面处连续变化，防止出现过大的跳跃，相邻的材料属性有较好的连续性，从而提高其计算精度和效率。本文基于分层法的思想，利用有限元分析软件ABAQUS分析功能梯度压电材料单裂纹在不同情况下的受力情况，研究了含单裂纹的功能梯度压电材料在改变梯度参数、几何尺寸和裂纹形状的条件下，功能梯度压电材料板的裂纹周围应力分布规律。本文结果可以为以后工程中设计功能梯度压电材料结构起到借鉴作用。

1 功能梯度压电材料基本方程

功能梯度压电材料场方程[4]为

(1)

应变和电场相容方程为

(2)

本构方程为

(3)

式中，σij、εij、Di和Ei分别是应力、应变、电位移和电场强度；ui为位移；φ为电势；cijkl为弹性模量系数；λik为介电系数；ekij为压电系数(i=x,j=y)。

对于功能梯度压电材料而言，因为功能梯度是在某一个方向上，材料参数按照特定函数，比如线性函数、指数函数、幂函数等的形式连续变化。本文研究的材料参数服从自然指数分布：

(4)

(5)

(6)

(7)

运用ABAQUS软件，根据有限元的基本理论，功能梯度压电材料的有限元中单元的耦合方程为

(8)

文中研究对象为二维平面，为平面应变状态，压电材料参数以x-y平面作为材料的等参面，x-z平面则为各向同性面。y轴方向作为极化方向，垂直于该平面，故本文研究是x-y平面问题。

2 建模仿真分析

本数值算例是以功能梯度压电材料PZT-5H作为研究对象，板左端的材料参数见表1。

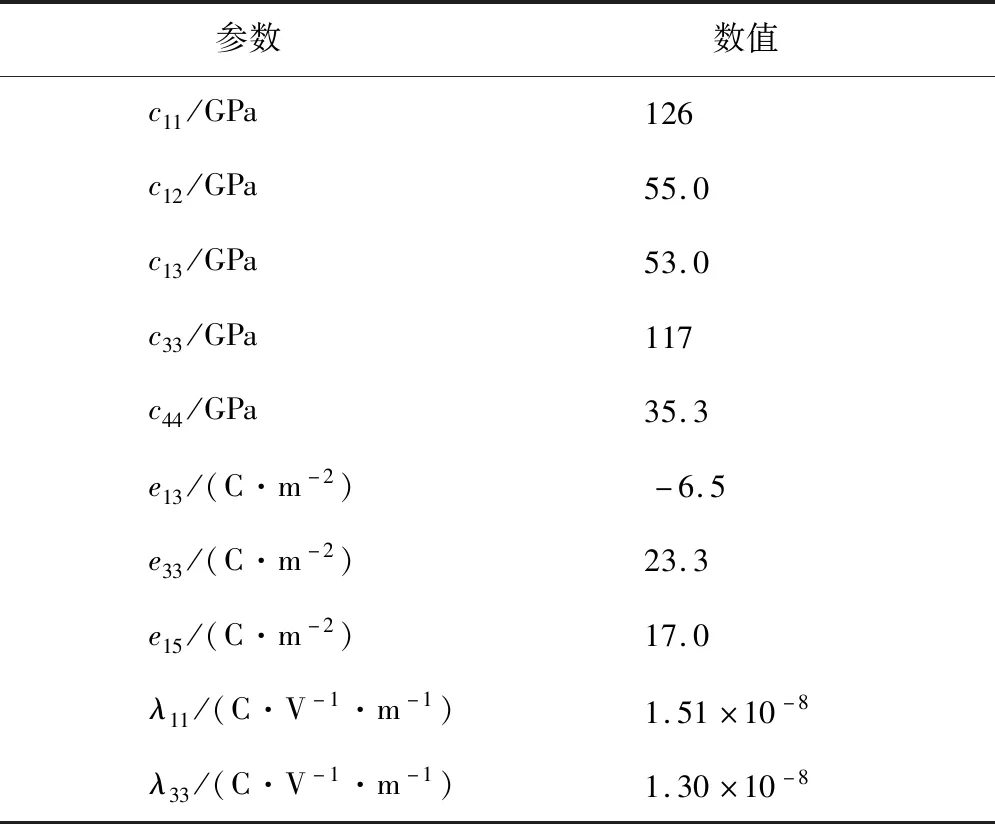
表1 PZT-5H压电材料参数Tab.1 Piezoelectric material PZT-5H parameters

简化后基本模型如图1，一块中心含圆形裂纹的二维正方形板，板边长a=80 mm，圆形裂纹半径r=0.5 mm。设置材料的极化方向为y轴正方向，材料的梯度变化方向为x轴正方向，板的左右两端AB与CD自由，板上下两端施加力边界，令施加均布应力100 MPa。材料参数梯度函数K=K0eβx，本例中取功能梯度参数β=0.01。

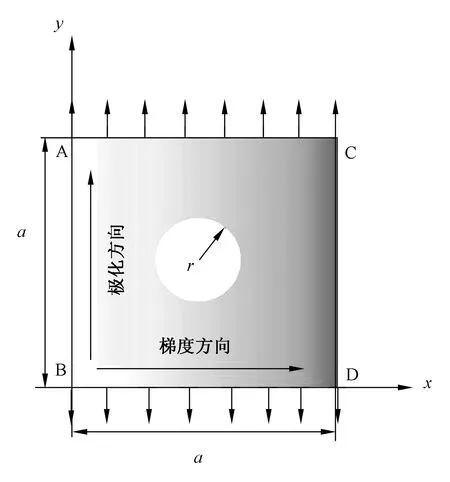
图1 功能梯度压电材料单裂纹板Fig.1 Single crack plate of functionally graded piezoelectric material

如图2建立有限元模型，根据分层法思想将功能梯度压电材料划分成若干层，每层的材料参数通过材料梯度函数计算得到，通过有限元软件定义每层的材料参数，从而达到近似拟合功能梯度材料的目的。在满足一定精度的条件下，将其分为14层。由于关注裂纹周围应力集中的情况，在圆形裂纹处进行细密分层，在较远处层间分层距离扩大，对结果影响不大。板有限元网格划分如图3所示，单元类型为8节点CPE8RE压电单元，线性缩减积分更准确地反应应力集中的情况，保证研究对象结果的准确性。

图2 含裂纹板的分层模型Fig.2 Delamination model of cracked plates

有限元计算最大主应力云图如图4所示，从图中可以看出，从裂纹边最大主应力值268 MPa到边上逐渐减小至16.86 MPa，最大主应力呈对称分布，在裂纹周围产生明显的应力集中，距离裂尖越远时，最大主应力越小。最大主应力最大的位置不在裂纹的尖端，而是在裂纹尖端的两侧，但左右不对称。这是由于材料梯度的变化，导致板左边的弹性模量小于右边的弹性模量，弹性模量是逐渐过渡增大，材料变得更加具有均匀性，从而避免了裂纹尖端的应力集中，使得应力分布较为均匀，限制了裂尖扩展的趋势，达到保护材料板不被破坏的目的。

图3 功能梯度板单元划分图Fig.3 Functional gradient plate element partition diagram

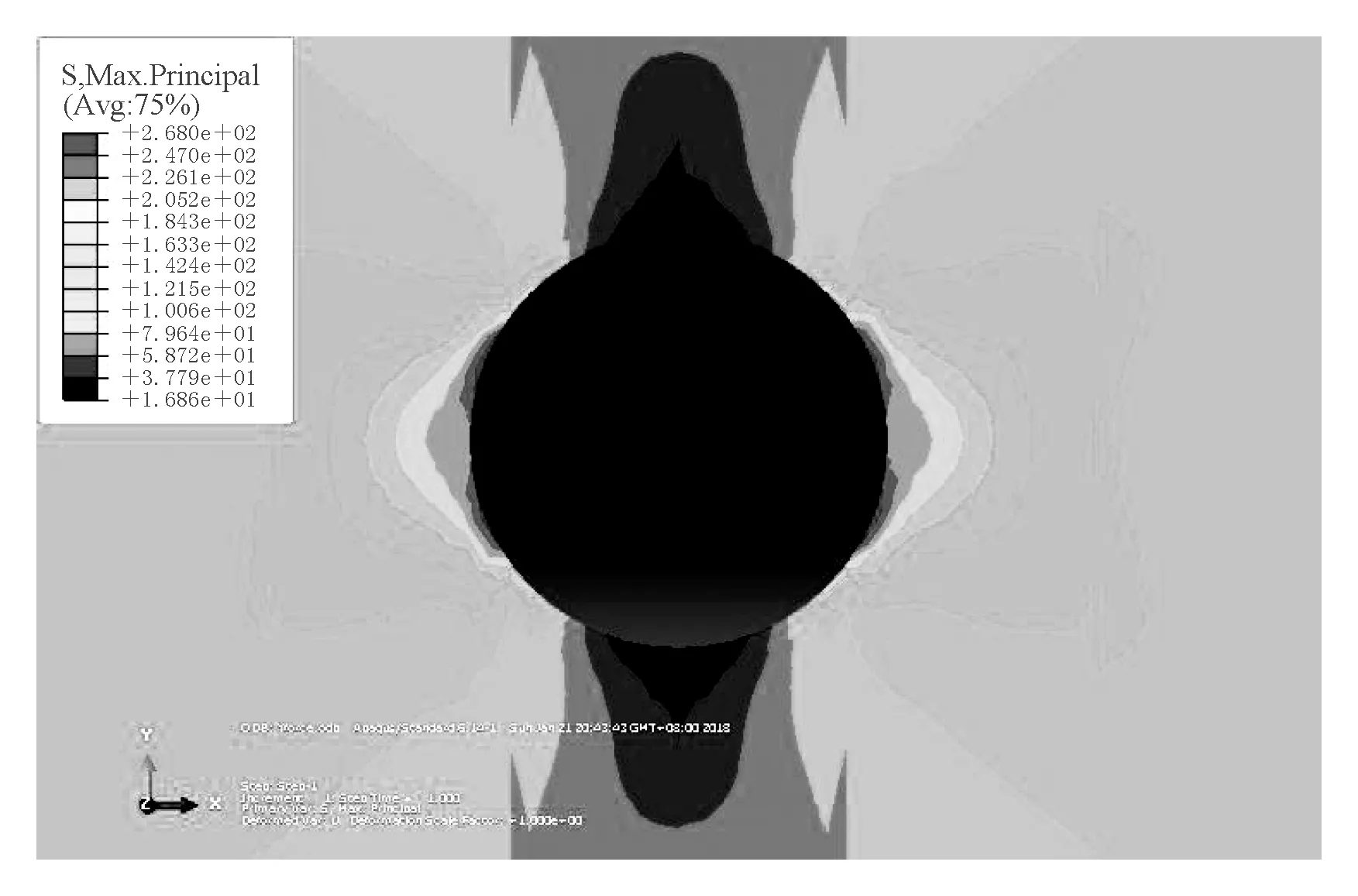
图4 最大主应力云图Fig.4 Maximum principal stress cloud diagram

3 不同参数的数值结果分析

3.1 不同功能梯度参数的圆形裂纹

令梯度参数β=0.02、0.03、0.04、0.05。通过软件计算得到应力分布云图，然后给出最大主应力如图5，可以看到随着功能梯度参数的增加，板从左到右弹性模量变化幅度增大，材料属性变化加快，从而使得材料过渡性变小，材料之间均匀性变差，产生应力集中现象更加明显，所以导致裂纹周围的最大主应力上升，材料更加容易发生破坏。

圆形裂纹环向应力σθ随着梯度参数的变化如图6所示，可以看到随着梯度参数的增加，环向最大应力增大。同时可以得到裂纹环向长度上的应力变化，可以看到最大σθ应力集中于裂纹尖端，在两个尖端处达到应力最大值，与实际力学情况相符。

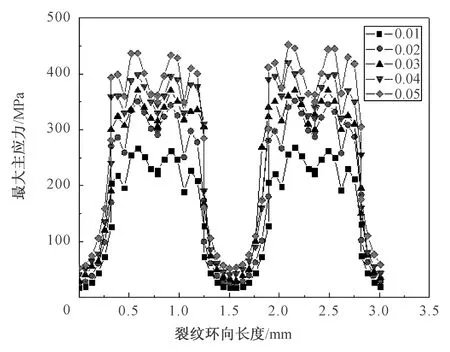
图5 圆形裂纹圆周上最大主应力分布图Fig.5 Distribution of maximum principal stress on circular crack circumference

图6 圆形裂纹圆周上应力分布图Fig.6 Distribution of σθ on the circumference of acircular crack

3.2 β=0.05时，不同半径的圆形裂纹

如图7所示，当板的大小不变时，改变圆形裂纹的半径,令圆形裂纹半径分别为0.2，0.5，0.8 mm，可以看到，圆孔附近发生了明显的应力集中现象。

当裂纹较小的时候，功能梯度材料应力集中在小的缺陷集中区域更加容易产生，且孔径越小应力集中越明显，应力突然变大的趋势变快，从而增大了裂纹边最大主应力与σyy应力。当裂纹的半径变大后，应力集中相比较变小，这与文献[15]结论相吻合。

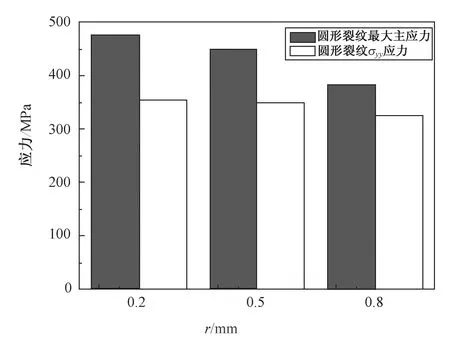
图7 不同半径的圆形裂纹最大主应力和σyy应力Fig.7 Maximum principal stress of circular crack with different radius and σyy

3.3 不同功能梯度参数的椭圆形裂纹

裂纹形状由圆形变为椭圆形，且椭圆形裂纹的长轴a=r=0.5mm，短轴b=0.2mm，同时改变功能梯度参数，令β=0.01，0.02，0.03，0.04，0.05。如图8与图9所示，椭圆形裂纹的应力随着梯度参数的变大而变大，这是因为材料均匀性变差，导致应力集中更加明显，这与图5中圆形裂纹的模拟结果相同。当在相同的梯度参数下，椭圆形裂纹的应力大于圆形裂纹的应力，应力集中现象更加明显，这是因为椭圆形裂纹与圆形裂纹相比，裂纹的形状更加凸出，导致更容易产生明显的应力集中，材料更容易发生破坏，这与文献[16]中结论相同。

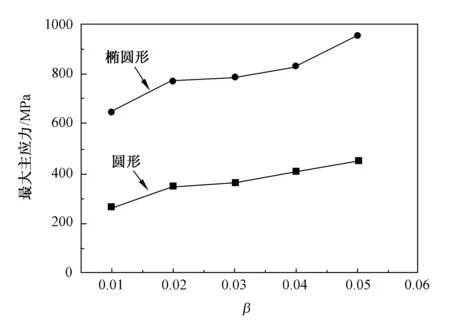
图8 圆形裂纹与椭圆形裂纹的最大主应力对比图Fig.8 Comparative diagram of maximum principal stress between circular crack and elliptical crack

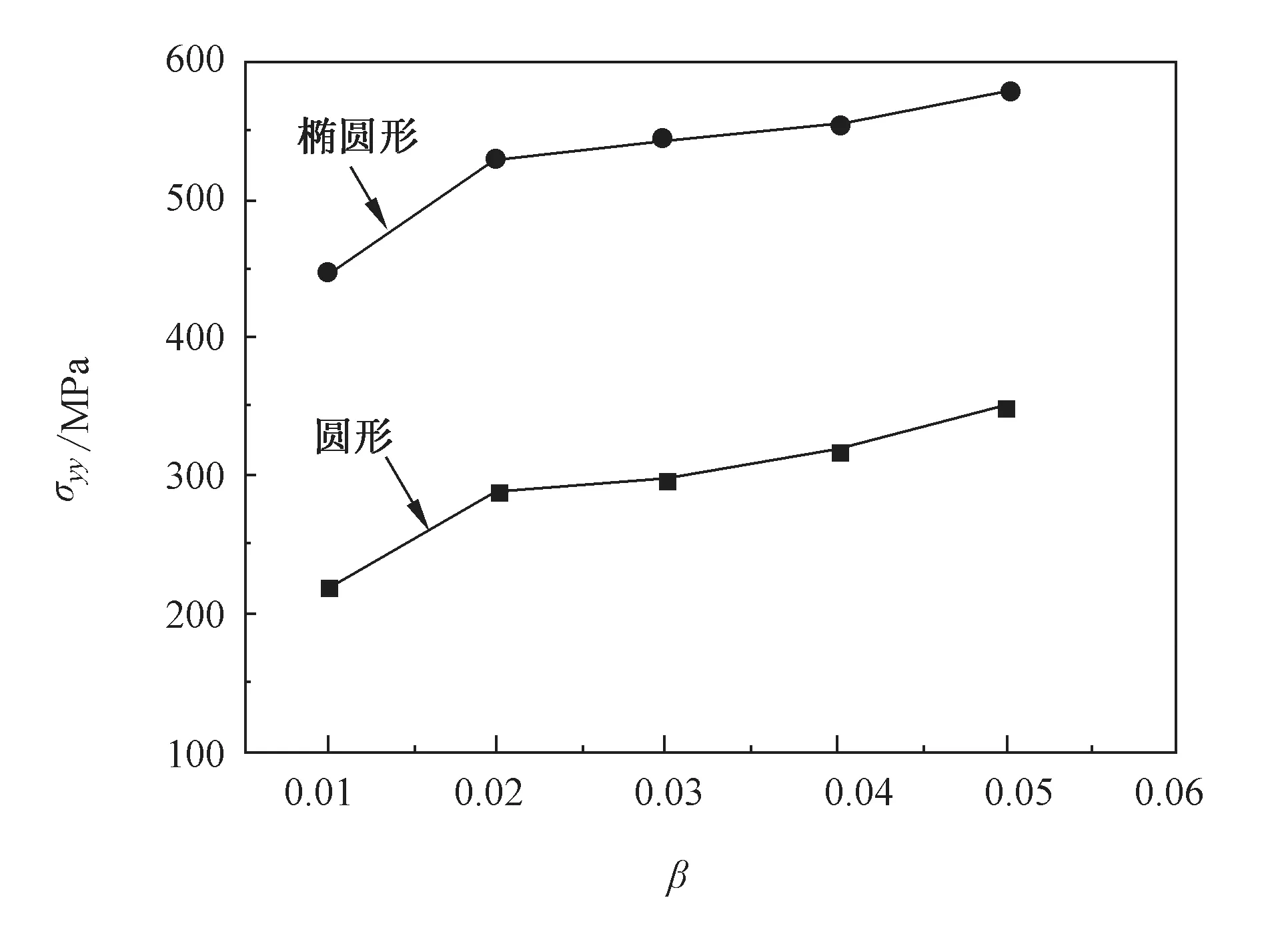
图9 圆形裂纹与椭圆形裂纹的σyy应力对比图Fig.9 Comparative diagram of σyy between circular crack and elliptical crack

4 结论

本文采用有限元软件ABAQUS对功能梯度压电材料单裂纹的力学问题进行了分析。基于功能梯度压电材料的本构关系、几何关系及边界条件，利用分层法的理论建立了功能梯度压电材料单裂纹的有限元模型。

通过改变功能梯度参数和裂纹半径尺寸，得到了参数变化对圆形裂纹的最大主应力和σyy以及环向应力σθ的影响规律；同时，对于不同功能梯度参数下的椭圆形裂纹，给出了最大主应力和σyy的变化规律，并与圆形裂纹的应力大小进行了对比。

圆形裂纹在不同的梯度参数下，最大主应力分别是所施加荷载的2～5倍左右，而应力σyy为所施加荷载的2～4倍左右。当梯度参数β=0.05，在不同半径的裂纹下，即r=0.2，0.5，0.8 mm时，得到了最大主应力分别是所施加荷载的4.7，4.5和3.8倍左右，而应力σyy分别是所施加荷载的3.5，3.4和3.3倍左右。