基于交织映射的16-QAM周期/非周期互补码集构造研究

刘 凯，孙向羽，张晓玲

(1.燕山大学 信息科学与工程学院，河北 秦皇岛 066004；2.燕山大学 河北省信息传输与信号处理重点实验室，河北 秦皇岛 066004)

0 引言

非周期互补码也称Golay互补码，是Golay互补对的扩展形式，它由两个以上的序列组成[1]。非周期互补码也是一类周期互补码，但周期互补码不一定满足非周期互补性质[2]。多个互补码中若任意两码的互相关函数和为零，那么就组成了相互正交的互补码集，简称为互补码集。互补码集应用于多载波通信系统时，每个用户分配一个互补码作为地址码，互补码的各序列调制到不同的载波上进行发送，因此互补码的数量决定了用户的数量，互补码的序列数代表着载波数。在接收端，同一用户信息在不同载波上的序列自相关函数之和为冲激函数，不同用户信息在不同载波上接收序列的互相关函数之和为零，以此消除了用户之间的干扰。若增大互补码中序列数量，则用户信息就可以调制到更多的载波上，因此在单位时间内传输的信息量增多，从而提高传输速率。近年来，正交幅度调制(QAM)序列设计得到了广泛关注，在通信系统中使用QAM序列作为地址码不仅可以提升系统的传输速率[3-4]，还可以降低系统的峰值与均值能量比(峰均比，PMEPR)[5-8]。为了增加具有最优相关特性的QAM序列的数量，学者们相继提出了16-QAM Golay互补对和互补码[9-12]，16-QAM周期/非周期互补码集及零相关区互补码[13-14]等。尽管这些构造结果扩大了具有良好自相关特性的16-QAM地址序列的范围，但目前构造16-QAM周期/非周期互补码集的方法和构造结果数量还不够丰富，因此本文为了扩展16-QAM周期/非周期互补码集的存在范围，构造了与以往文献不同的互补码集，从而扩大实际应用中地址码的选择空间。

本文提出了三种适应于周期/非周期序列的交织映射方法，得到大量新的16-QAM周期/非周期互补码集，互补码中序列的数目可以灵活选择，同时在多载波系统中提高了单位时间内的信息传输速率。

1 基本概念

定义1 设a=(a(0),a(1),…,a(L-1))和b=(b(0),b(1),…,b(L-1))是长度为L的复序列，a与b的周期和非周期相关函数分别表示为

(1)

(2)

若a=b，式(1)和(2)分别称为序列a的周期和非周期自相关函数，记为Ra(τ)和Ca(τ)，其中b*是b的复共轭形式。

(3)

(4)

那么集合S分别称为周期互补码集和非周期互补码集(即Golay互补码集)，表示为PCCS(M,N,L)和ACCS(M,N,L)，Sm称周期/非周期互补码，表示为PCC(N,L)和ACC(N,L)，其中M表示集合S包含Sm的数量，N表示Sm包含序列的数量，L表示序列长度。

定义3 16-QAM星座由如下字母集表示，

(5)

其中j表示复数单元，j2=-1。

引理1[1,7,12]四元坐标a,b∈{1,2,3,4}到16-QAM星座坐标映射方法有如下四种：

(6)

其中，σ1由文献[7]提出，σ2由文献[1]提出，σ3和σ4由文献[12]提出。

引理2[14]基于四元周期/非周期互补码集S，参数为PCCS(M,N,L)或ACCS(M,N,L)，若周期/非周期互补码Sm的序列数量N为偶数，即N=2N′，通过以下方法可以得到参数为PCCS(M,N,L)或ACCS(M,N,L)的16-QAM的周期/非周期互补码集G，

(7)

2 16-QAM序列集的三种交织映射构造方法

基于四元周期/非周期序列集S以及引理1，提出以下3种交织映射方法，将S中的元素映射到16-QAM星座上。

方法1：

(8)

(9)

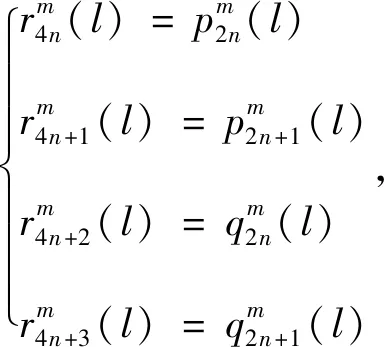
(10)

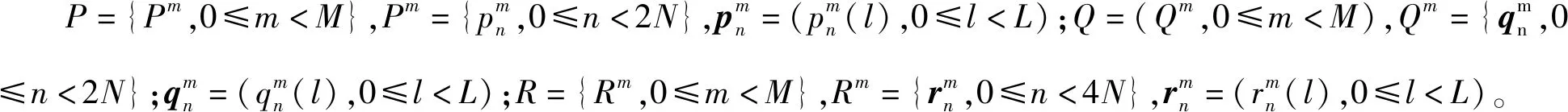
方法2：

将引理2推广至σ3,σ4的映射中，若Sm包含序列数量N为偶数，即N=2N′，可得到序列长度为N的16-QAM序列集T，

(11)

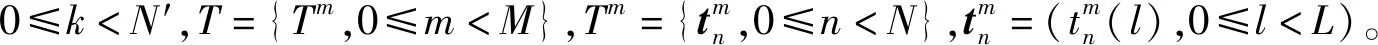
方法3：

结合引理2及方法2，构造集合W。若Sm包含序列数量N为偶数，即N=2N′，通过如下操作可得到2N长16-QAM序列集W，

3 16-QAM周期/非周期互补码集

定理1 若S是参数为PCCS(M,N,L)/ACCS(M,N,L)的四元周期/非周期互补码集，则集合P、Q、R、T、W是参数分别为PCCS(M,2N,L)/ACCS(M,2N,L)、PCCS(M,2N,L)/ACCS(M,2N,L)、PCCS(M,4N,L)/ACCS(M,4N,L)、PCCS(M,N,L)/ACCS(M,N,L)、PCCS(M,2N,L)/ACCS(M,2N,L)的16-QAM周期/非周期互补码集。

为了证明定理1需要以下3个引理。

引理3 方法1中集合P、Q、R的相关函数值满足

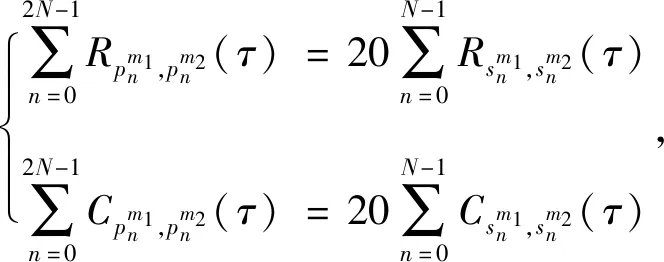
(13)

(14)

(15)

证明由于非周期相关函数的计算与周期相关函数的计算相似，在以下证明中只计算周期相关函数值。取Pm1,Pm2⊂P,

(16)

其中，

(17)

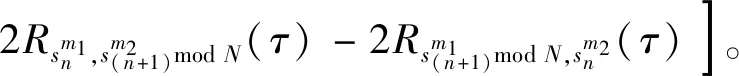
(18)

将式(17)、(18)带入式(16)，有

(19)

同理可证集合Q的相关函数值满足式(14)。下面计算集合R的相关函数满足式(15)，取Rm1,Rm2⊂R,

(20)

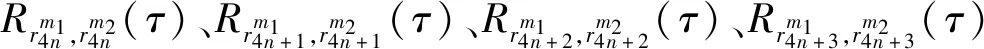
(21)

故引理3成立。

证毕

引理4 方法2构造的集合T的相关函数值满足

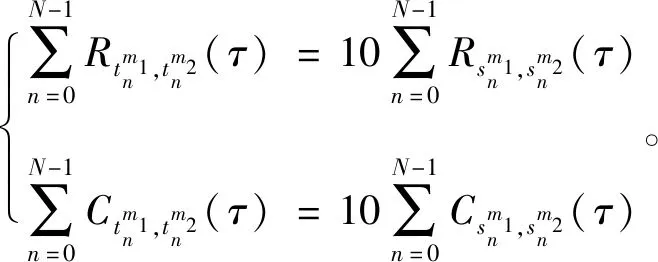
(22)

证明与引理3的证明过程类似，取Tm1、Tm2⊂T，

(23)

由此，引理4成立。

证毕

引理5 方法3得到的集合W的相关函数值满足

(24)

证明取Wm1、Wm2⊂W，

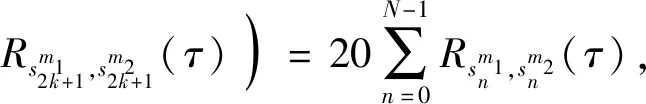
(25)

故引理5成立。

证毕

下面证明定理1，由于非周期互补都是周期互补的，相反却不成立[2]，加之篇幅的限制，本文只证明周期互补情况。

证明由于S是参数PCCS(M,N,L)的四元周期互补码集，所以周期相关函数满足

(26)

将式(26)分别带入引理3、4、5中，得到集合P、Q、R、T、W的相关函数为

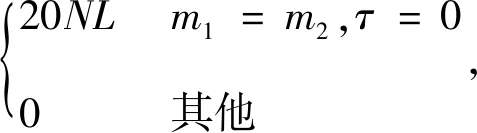
(27)

(28)

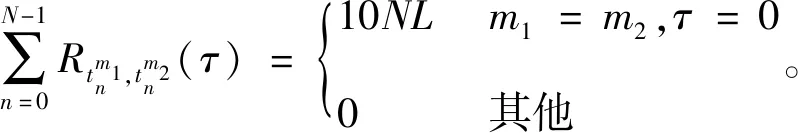
(29)

由定义2可知，集合P、Q、R、T、W均是周期互补码集，同理可证非周期互补特殊性亦成立，定理1成立。

证毕

例选取参数为ACCS(4，4，4)的四元非周期互补码集

由定理1可得到集合P、Q、R、T、W。下面只列出集合P、Q、R、T、W的其中一个互补码：

经计算，集合S的互补码非周期自相关函数是(0,0,0,16,0,0,0)，集合P、Q、R、T、W的非周期自相关函数分别是(0,0,0,320,0,0,0)、(0,0,0,320,0,0,0)、(0,0,0,640,0,0,0)、(0,0,0,160,0,0,0)、(0,0,0,320,0,0,0)，其互相关函数值均为0，所以集合P、Q、R、T、W分别是参数为ACCS(4,8,4)、ACCS(4,8,4)、ACCS(4,16,4)、ACCS(4,4,4)、ACCS(4,8,4)的16-QAM非周期互补码集。

文献[7]中证明，若采用四元Golay序列(即Golay互补对中的组成序列之一)作为基序列，通过式(6)σ1的映射操作可得到具有低PMEPR性质的16-QAM序列。此结论可推广到其他三种映射，因此若四元非周期互补码集的组成序列由Golay序列构成，那么通过本文映射方法得到的16-QAM非周期互补码集可具有低PMEPR的性质。

4 16-QAM周期/非周期互补码集参数及性能分析

本文提出了3种获得16-QAM周期/非周期互补码集的交织映射方法，根据不同交织方法，利用相同四元周期/非周期互补码集可得到5类不同构造结果、不同集合参数的16-QAM周期/非周期互补码集。文献[14]同样利用了交织映射的方法构造周期/非周期互补码集，在表1中与其进行了详细对比。

表1 构造方法对比表Tab.1 Comparison of the construction methods

本文以四元周期/非周期互补码集为基础码集，现有文献为其提供了较丰富的构造方法和构造结果[15]，保证了本文构造方法的实现。互补码中，码速率计算公式为R(Sm)=log2|Sm|/L比特/符号[10]，其中|Sm|表示互补码Sm的序列数量N，L表示序列长度，可见在L不变的情况下，增大互补码Sm的序列数量有利于提升码速率。由于码速率仅与N和L有关，因此表2比较了所构造的16-QAM周期/非周期互补码与基础四元互补码的码速率提升对比值。

表2 码速率提高比率对比表Tab.2 Comparison of the ratio of code rate increase

由表2可以看出，本文构造的周期/非周期互补码与四元基础序列的码速率比值均大于1，与其他文献相比也有提高，因此本文构造方法通过增大互补码的序列容量提升了单位时间内信息的传输量。

5 结论

本文提出了3种将四元周期/非周期互补码集交织映射为16-QAM周期/非周期互补码集的方法，获得了新的参数形式，成倍地提高了互补码中序列的数量。本文提出的方法有效地增加了16-QAM周期/非周期互补码集的存在范围，可用以提升多载波通信系统的传输速率。