基于改进粒子滤波的LiFePO4电池二元SOC估算

孙叶宁，魏艳君，赵 勇，漆汉宏,*，陈洪涛

(1.燕山大学 河北省电力电子节能与传动控制重点实验室，河北 秦皇岛 066004；2.国网吉林省电力有限公司松原供电公司，吉林 松原 138000)

0 引言

电动汽车时代即将到来，磷酸铁锂电池是电动汽车的主要动力来源，是本文的研究对象。电池管理系统(Battery Management System，BMS)是纯电动汽车的重要组成部分，荷电状态(state of charge，SOC)估算是BMS主要功能之一，准确估算电池SOC，可最大限度发挥电池的工作性能，延长电池使用寿命。但蓄电池SOC无法直接测量，电池本身又呈现高度非线性工作特性；此外，在不同的充放电倍率下，电池还会呈现可用容量弹性变化以及容量恢复等倍率容量特性，这也提高了SOC估算的难度[1-3]。

近年来随着SOC估算技术的深入研究，一些新颖的思路不断涌现，推动着BMS不断发展。安时积分法由于其简单、高效，在实际工程中得到大量运用，但是该算法对SOC初始值无法定位，长时间使用会导致累积误差不断扩大，尤其是在高温和电流充放电倍率频繁突变的情况，因此后期处理需要对其校正[4]。开路电压法是通过长时间静置(>1 h)使电压恢复开路电压，具有简单方便、易于实现的优点；长时间的静置虽然能够稳定电池的工作状态，但是在一定程度上电池会产生自放电效应，造成电池容量浪费[5]。卡尔曼滤波(Kalman Filter，KF)算法在一定条件下能够对SOC进行有效估算，只是算法对模型较为依赖，对电池参数敏感，且经过线性化处理后难免存在误差[6-8]。在此基础之上，改进后的卡尔曼滤波算法已成为当下研究的热点。美国科罗拉多大学Gregory L.Plett教授围绕扩展的卡尔曼滤波(Extended Kalman Filter，EKF)、递推最小二乘等算法在电池SOC/SOH估算技术中的应用进行了详尽分析[9-10]，得到了学术界和工业界的普遍认可；美国北卡罗来纳州立大学ADAC实验室的Mo-Yuen Chow团队在电池模型参数、SOC和SOH统一自适应在线辨识技术方面也取得一定成果[11]；文献[12]基于改进的Thevenin模型，利用双卡尔曼滤波算法(Dual Extended Kalman Filter，DEKF)在线辨识电池欧姆内阻R0参数；同时基于改进的Thevenin模型，利用DEKF对SOC进行实时估算，该算法具有较好的精确度和收敛性。文献[13]基于锂电池Thevenin模型，采用带遗忘因子的递推最小二乘算法(Forgetting Factor Recursive Least-squares，FFRLS)在线辨识Thevenion模型参数R0、Rp、Cp和Uoc。考虑到EKF局部线性化过程中会使最终结果引入误差，因此这里引入灰色预测模型(Grey Prediction Model，GM)代替EKF算法局部线性化，对当前时刻系统状态做先验估算；再通过观测方程对其进行更新修正，得到后验估算值，实现对SOC的估算。文献[14]基于改进的PNGV电池等效模型，模型是在原有PNGV的基础上串联一阶RC，同时采用扩展卡尔曼滤波算法对SOC进行估算，模型参数辨识采用离线方式，没有考虑初始SOC误差对估算结果的影响。文献[15]中以二阶RC等效电路模型为研究对象，基于Sage-Husa自适应滤波思想，提出一种自适应平方根无迹卡尔曼滤波算法，该方法研究状态方差阵和噪声方差阵平方根的递推估算，确保状态和噪声方差阵的对称性和非负定性，具有较高的稳定性和自适应性，相比传统平方根无迹卡尔曼滤波算法，该算法中包含两个UT变换，且引入自适应滤波算法，计算量大，难以在实际工程中广泛应用。除此之外，基于电化学模型的SOC估算方法近年来备受关注，美国加州大学的M.Doyle和J.Newman等基于多孔电极和浓溶液理论建立了准二维多孔电极(Pseudo two dimensional，P2D)模型。该模型采用偏微分方程组对电池负极、隔膜和正极区域内的法拉第效应、电极内部锂离子扩散及表面电化学反应、电解液中锂离子扩散与迁移等物理和化学过程进行了详细描述。P2D模型作为锂离子电池的基础性电化学模型一直被广泛使用[16-17]，虽然得到的模型精度很高，但是模型涉及非线性偏微分方程组，计算量大，很多内部参数也难以获得，故未实现广泛应用。

本文将KiBaM二元SOC模型和Thevenin模型结合起来建立综合模型，并引入改进粒子滤波(Particle Filter，PF)算法对SOC进行估算。该方案可有效跟踪电池倍率容量特性，实验结果验证了该方案的可行性，与常用的卡尔曼滤波算法对比，该算法具有更强的系统噪声处理能力，能够处理非线性、非高斯问题，是一种通用的贝叶斯滤波方法。

1 蓄电池综合模型

1.1 KiBaM基本思想

电池模型的建立以经典的Thevenin 模型为基础，引入较明确对蓄电池容量特性进行描述的KiBaM模型(双井模型)，进而将Thevenin模型与KiBaM模型相结合形成综合模型，如图1所示。综合模型中hmax表示蓄电池双井的最大高度；y1、y2等效为面积，表示两井中的电量；h1、h2分别表示可用井和受限井当前存储电量的高度；w、1-w分别表示可用井和受限井当前存储电量的宽度；S1和S2分别可用井和受限井的荷电状态；S为蓄电池的荷电状态；k为两井间阀门的电导系数，也可以理解为可用井恢复系数。R0是欧姆内阻；R1是极化电阻；C为极化电容；uc表示极化电容电压；V是电池端电压。

1.2 KiBaM离散模型

KiBaM模型采用两个井描述电池特性，它是一种基于感性认识的方法。具体表现为：

1) 倍率容量特性：放电电流越大，能够放出的容量越小。

2) 容量恢复特性：在放电过程中，能量从可用井y1的右下角流出；同时受约束井y2能量通过通道流入可用井y1。

根据模型可得到微分方程为

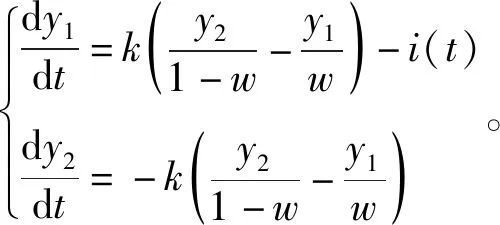
(1)

对KiBaM模型进一步推导，目的是让最终的综合模型建立与SOC的直接关系。现对式(1)两侧同时除以电池额定容量Qb可得

若将电池的荷电状态视作两个容量井荷电状态之和，令x1=S1，x2=S2，描述成状态空间方程的形式为

(2)

以上为连续KiBaM模型，为便于后续的工程实现，需将该模型离散化。结合式(2)，连续KiBaM模型对应的离散模型可以描述为以下形式

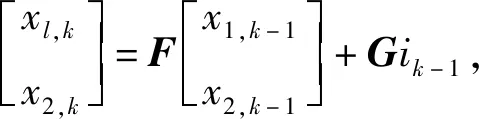
(3)

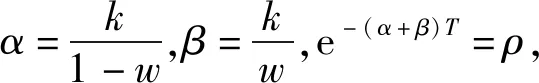
式(3)为适用于SOC估算的离散模型。关于KiBaM模型中参数k和w的获取，本文是采用离线多倍率放电测试配合统计分析法进行提取。首先，针对所研究电池样本，在充满电状态下采用多种倍率方式进行放电测试，直至电池电压到达下限2.5 V。然后，根据不同倍率下电池可以放出的实际容量采用离线统计分析手段，再结合循环仿真寻优，可以获得对应型号蓄电池的KiBaM模型参数k和w。最后，将以上结果与Thevenin模型[18]取得联立，得出离散状态空间综合模型为

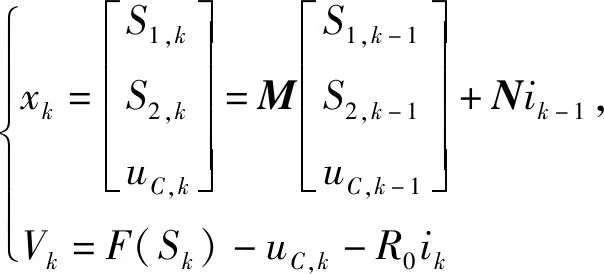
(4)

其中，

实验中采用LiFePO4电池，根据工程经验及离线数据拟合优化分析方法，获取参数值分别为w=0.85、k=9.5×10-5。Sk=S1,k+S2,k，而F(Sk)对应k时刻图1模型中的电池电动势E；E-S曲线的获取是将充满电的电池以0.05 C倍率恒流放电到下限截止电压2.5 V，静置3 h后，再以0.05 C倍率恒流充电到上限截止电压3.65 V，最后对两条曲线取平均得到。

2 基于改进PF的电池SOC估算

目前EKF和无迹卡尔曼滤波(Sigma Point Kalman Filter，SPKF)广泛用于蓄电池SOC估算，但是，它们假设状态变量均为高斯随机变量，一般都将系统噪声和观测噪声视为零均值的高斯白噪声，这使其对于非高斯、非零均值噪声的处理能力受到限制，进而引入误差。PF是一种基于蒙特卡罗仿真的近似贝叶斯滤波算法，核心思想是用离散随机采样的粒子表达系统随机变量的概率密度分布，与SPKF等方法相比，它对状态变量没有任何限制，能够处理非线性、非高斯问题，是一种通用的贝叶斯滤波方法，本方案电池SOC估算即采用一种改进的粒子滤波算法[19-20]。

改进PF算法是在标准粒子滤波算法的基础上，进一步引入残差重采样及Thompson-Taylor算法，如图2所示。

此算法的优势，一方面，残差重采样算法可以有效解决粒子退化问题；另一方面，通过Thompson-Taylor算法可对粒子进行随机线性组合，生成新粒子，可以抑制标准PF过程中出现的粒子贫化问题，产生的新粒子保证了粒子的多样性，能更好地适应蓄电池的非线性工作特性，从而实现对SOC的准确实时估算。

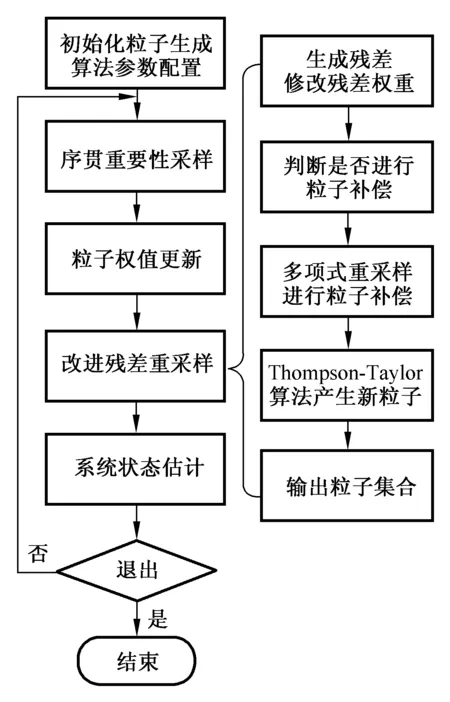
图2 改进PF算法流程图Fig.2 Flowchart of improved PF

2.1 基于标准PF的SOC估算

对于某非线性动态系统，其状态空间模型可描述为

对于本文来讲，该模型即为式(4)给出的综合电池模型。其递推步骤如下。

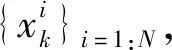
q(xk|x0:k-1(i),y1:k)=p(xk|xk-1(i))。

3) 权值更新及归一化：获得了k时刻观测值后，可对权值更新，进而做归一化处理为

如果单纯将原始系统观测模型作为增量权，则无法利用最新观测信息对粒子的权值进行有效修正，为保证粒子可依据各自的贡献大小获得相应的权值分配，在此引入Bhattacharyya距离的思想，结合高斯概率密度分布对似然函数进行重新构造为

其中,σ是高斯分布的方差。

4) 重采样：基本思想是繁殖权值较高的样本而淘汰权值较低的样本，重新生成一个新样本集合以克服样本退化。本文采用残差重采样，具体实现步骤见2.2节。

5) 系统状态估计为

6) 当前拍算法完成，回到序贯重要性采样步骤。

2.2 改进残差重采样算法

标准PF算法基于序贯重要性采样，存在粒子退化问题，即经过若干次采样后，重要性权值将集中在少数粒子上，这些粒子将不足以准确表征后验概率密度函数。为解决该问题，有人提出了重采样算法，主要思想是去除小权值粒子，复制大权值粒子。本方案中采用残差重采样更新粒子，采用多项式重采样进行粒子补偿。此外，多次进行重采样算法会产生粒子贫化问题，丧失了粒子的多样性。对此，本方案采用Thompson-Taylor算法对残差重采样结果随机线性组合产生新粒子，得到一种改进残差重采样算法。改进残差重采样算法步骤如下。

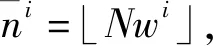
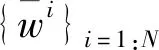
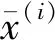
③ 产生m个均匀分布随机数uj为

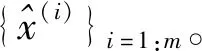
以上递推过程中，需要确定平滑系数m。这里采用实验的方式，比较在不同粒子数N和平滑系数m下SOC估算误差曲线，择优选取。一般取值为m=3N/10。

3 基于改进PF及RLS的SOC估算

蓄电池综合模型的等效参数是通过递推最小二乘(Recursive Least-squares，RLS)算法来获取的，RLS的基本思想为本次估计值等于上次估计值与修正值之和。算法无需存储和计算历史数据，代码执行效率较高，便于实现快速准确在线辨识。RLS详细分析参见文献[21],在此不做展开。

SOC估算框架如图3所示，本文将改进PF和RLS算法相结合，同时实现对电池模型参数的辨识和SOC的估算。RLS启动初值由前60组外特性采样值计算获得，RLS迭代过程需要用到电池电动势E，为上一拍估算出的SOC所对应的电动势E；RLS辨识得到模型参数R0、R1和C可代入综合模型，进而配合改进PF算法估计出系统状态；将估算得到S1、S2相加即得到S，再通过E-S关系查表可获得当前时刻的电动势E，用于下一拍RLS辨识。如此循环迭代，形成完整的耦合结构，实现对电池二元SOC的准确实时估算。

图3 整体SOC估算框架Fig.3 Framework of general SOC estimation

4 实验与分析

基于以上分析，对该方案进行了实验测试。该实验平台由锂离子电池和充放电系统组成。锂离子电池采用的是美国A123公司生产的26650型3.2 V/2 500 mAh的LiPePO4电池。充放电系统由杭州德康DT50W-16高精度单体测试仪和上位机组成。为了能够充分体现电池脉冲充放电性能，检验SOC估算的动态响应能力，采用模拟动态工况的随机脉冲充放电方式。

随机脉冲充放电实验电池外特性，如图4所示。为了便于对比，在相同的蓄电池模型以及模型参数辨识算法一致的条件下，本研究分别采用扩展卡尔曼滤波和改进PF算法对电池SOC进行估算。

图4 电池随机充放电测试外特性Fig.4 Battery external characteristic during random charge/discharge test

图5为传统SPKF算法获得的SOC估算结果。电池荷电状态S由两部分组成，分别是电池可用井容量的荷电状态S1和受限井容量的荷电状态S2。S1的变化率明显高于S2的变化率，传统SPKF算法的SOC估算结果，S估算误差保持在±6%，当SOC在40%～60%区间时，误差大于4%。出现此现象可能是由于电池在此阶段电动势变化率小，算法在这个阶段修正能力较弱。

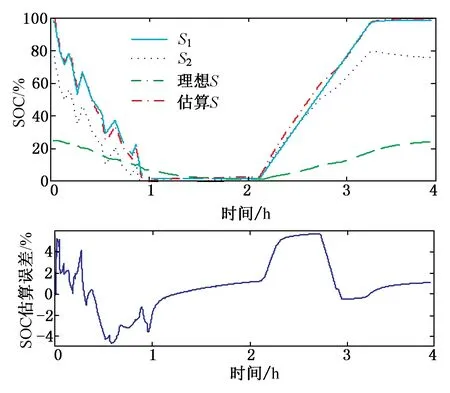
图5 基于传统SPKF算法的SOC估算结果Fig.5 SOC estimation results based on traditional SPKF algorithm

图6为基于改进PF算法的二元SOC估算结果。在整个测试过程中，S2的变化率明显低于S1的变化率，这是由电池厂商生产工艺和模型参数决定的。

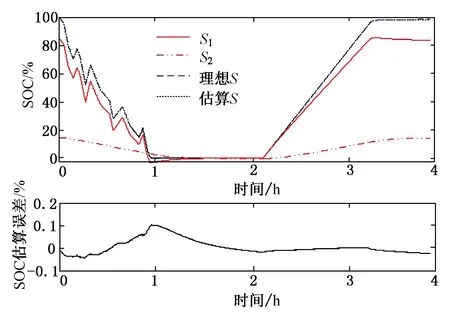
图6 基于改进PF算法的二元SOC估算结果Fig.6 SOC estimation results based on improved particle filter algorithm

随机充放电阶段末期(1 h前后)达到电池截止电压，可用井容量已被放空，受限井还存在小部分容量；随后经过一段长时间的静置过程，此时由于电流0，S保持不变，可用井容量S1逐渐增大，受限井容量S2逐渐减少；而恒流充电完成后也存在一段静置过程，S同样保持不变，可用井S1逐渐减少，受限井S2逐渐增大，这清晰描述了可用井与受限井两者之间的电荷转移过程，也充分体现了蓄电池的容量恢复特性，这与实际工况中电池在充放电结束后的静置阶段可用容量会发生变化的特性一致。基于改进PF算法的二元SOC估算结果，S估算误差保持在±0.2%之间。

通过两种算法对比可以发现，基于改进的粒子滤波二元SOC估算在荷电状态估算过程中精度较高，估算误差小于SPKF算法，并未出现SPKF算法中的局部误差较大现象，且在倍率突变工况估算中具有明显优势。

5 结论

结合Thevenin模型与KiBaM模型构建LiFePO4电池综合模型，采用RLS算法准确辨识锂离子电池模型参数。在标准PF算法的基础上，通过改进重采样部分，生成新粒子，提高粒子的多样性，解决了粒子贫化问题，有效提高了滤波性能，提高了估算电池SOC的准确性。通过实验测试，对比SPKF和改进的PF算法，估算电池SOC，结果表明，改进的PF算法能准确跟踪和估算电池SOC，整体估算误差不超过±0.2%，与SPKF算法相比，具有更高的估算精度。该方法有更强的实际噪声处理能力，能够更加准确地跟踪电池实际工作性能。结果表明，该方法估算出的二元SOC可以有效描述电池的倍率容量特性及容量恢复等特性，工程应用价值较高。