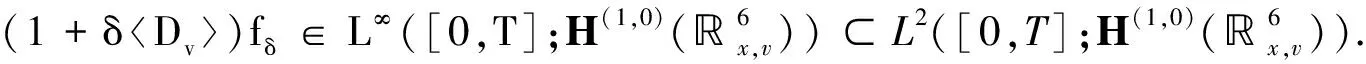线性Fokker-Planck方程柯西问题解的适定性
2019-12-25李浩光刘静
李浩光,刘静
(中南民族大学 数学与统计学学院,武汉 430074)
1 相关知识
这篇文章主要研究的是线性Fokker-Planck方程的柯西问题解的适定性. 考虑线性Fokker-Planck方程的柯西问题:
(1)
其中f=f(t,x,v)取决于时间t≥0,位置变量x∈3,速度变量v∈3.
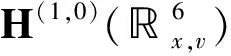
其中:
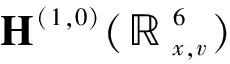
2 定理1的证明
定理1对于0
‖f‖L∞([0,T];H(1,0)(6))+‖vf‖L2([0,T];H(1,0)(6))≤
(2)
我们将定理1的证明分为两部分,首先利用Hahn-Banach延拓定理,在Sobolev空间证明命题1,从而证明方程存在唯一弱解,然后在速度变量上对弱解的正则性进行估计.
2.1 解的局部存在唯一性
命题1对于0 满足: 证明我们考虑伴随算子: P*=-∂t-v·x-Δv-v·v, Re(ψ(t),P*ψ(t))(1,0)= Re(ψ,Δvψ)(1,0)-Re(ψ,v·vψ)(1,0)= Re(v·xψ,ψ)(1,0)-Re(ψ,v·vψ)(1,0). 因为对于0≤t≤T,可知: Re(v·∂xψ,ψ)(1,0)=0,v·v=3. 利用Cauchy-Schwartz不等式,可以得到: 2‖ψ‖(1,0)‖P*ψ‖(1,0), 2e6t‖ψ‖(1,0)‖P*ψ‖(1,0). 因为ψ(T)=0,我们有: 2e6T‖ψ‖L∞([0,T];H(1,0)(6))‖P*ψ‖L1([0,T];H(1,0)(6)), 所以: ‖ψ‖L∞([0,T];H(1,0)(6))≤ 2e6T‖P*ψ‖L1([0,T];H(1,0)(6)). (3) 接下来,考虑向量子空间: ψ(T)=0}⊂L1([0,T];H(1,0)(6)), 因为f0∈H(1,0)(6),我们可以定义线性函数: Q:→, u=P*ψ|→(f0,ψ(0))(1,0), |Q(u)|≤‖f0‖(1,0)‖ψ(0)‖(1,0)≤ ‖f0‖(1,0)‖ψ‖L∞([0,T];H(1,0)(6))≤ 2e6T‖f0‖(1,0)‖P*ψ‖L1([0,T];H(1,0)(6))= 2e6T‖f0‖(1,0)‖u‖L1([0,T];H(1,0)(6)). 利用Hahn-Banach定理,Q可以在L1([0,T];H(1,0)(6))推广为连续线性形式,且其范数小于根据Riesz表示定理,存在唯一的f∈L∞([0,T];H(1,0)(6))满足: 使得: ∀u∈L1([0,T];H(1,0)(6)), Q(P*ψ)= 因此f∈L∞([0,T];H(1,0)(6))是柯西问题的唯一弱解.假设是柯西问题的另一个弱解,满足: 这部分将估计不等式(2),从而完成定理1的证明. 利用命题1,可以得到柯西问题(1)有唯一弱解: 我们将证明这个解满足不等式(2). 定义: fδ=(1+δDv)-1f,0<δ≤1, 利用文献[6]第5.9节中的定理3,可以得到映射: 是绝对连续的,且有: 将上述柯西问题(1)的方程与(1+δDv)-2Dv2f作内积并积分可得: 0=(∂tf+v·xf-Δvf-v·(vf), Re(v·xDvfδ,Dvfδ)L2- Re(Δvf,(1+δDv)-2Dv2f)L2- Re(v·(vDvfδ),Dvfδ)L2. 因为对于所有函数ψ∈S(6),有: Re(v·xψ,ψ)L2=0, 于是有: 由Gronwall不等式,对于所有0≤t≤T,存在一个正常数c>0,使得: 当δ→0时,可得: ‖f‖L∞([0,T];H(1,0)(6))+‖vf‖L2([0,T];H(1,0)(6))≤ 定理1得证.
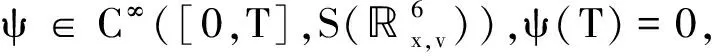
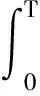
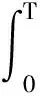
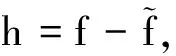
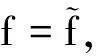
2.2 在速度变量上的正则性估计