一类分数阶Cohen-Grossberg神经网络的有限时间稳定性分析
2019-12-25杨占英李静文杨玺
杨占英,李静文,杨玺
(中南民族大学 数学与统计学学院,武汉 430074)
分数阶神经网络在数据优化、信号处理、联想记忆、并行计算、模式识别、人工智能等方面有着非常重要的应用,而其主要因素是人工神经网络的动态行为,特别是稳定性.因此,分数阶神经网络的稳定性问题已经成为目前最活跃的研究课题之一.随着研究的不断扩大,多种不同的稳定性不断涌现,例如:指数稳定性、有限稳定性、一致稳定性和Mittag-Leffler稳定性等.Cohen-Grossberg神经网络模型是由Cohen和Grossberg在1983年构造的,该模型包含了熟知的Hopfield神经网络和细胞神经网络,因此更具有一般性,它在信号处理、联想记忆和最优化问题等方面有着非常重要的应用价值.对于Cohen-Grossberg神经网络的有限时间稳定性问题,已有大量的文献进行了深入的研究.然而,这些研究所涉及的主要是整数阶Cohen-Grossberg神经网络.由于分数阶微积分理论的复杂性,这些结论并不能完全推广至分数阶Cohen-Grossberg神经网络,因此对于分数阶Cohen-Grossberg神经网络稳定性的研究是很有必要的.目前,已经有少量的文献对于分数阶Cohen-Grossberg神经网络的稳定性进行了不同的研究.例如,ZHENG 等在文献[1]中研究了一类分数阶忆阻Cohen-Grossberg神经网络的有限时间稳定性和同步问题;YANG 和LI 在文献[2]中研究了一类分数阶Cohen-Grossberg神经网络的有限时间稳定性问题;WAN和WU在文献[3]中研究了一类有偏差变元的分数阶模糊Cohen-Grossberg神经网络的Mittag-Leffler稳定性问题.
本文对于阶数在(0,0.5]和(0.5,1)的分数阶Cohen-Grossberg神经网络达到有限时间稳定的问题分别给出了一个充分条件,通过MATLAB仿真验证了其有效性.
1 基础知识
首先回顾Caputo导数的定义和一些重要不等式.
定义1[4]f(t)是R上的连续函数,对于任意的α∈[0,+∞),f(t)的α阶积分定义为:
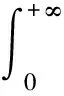
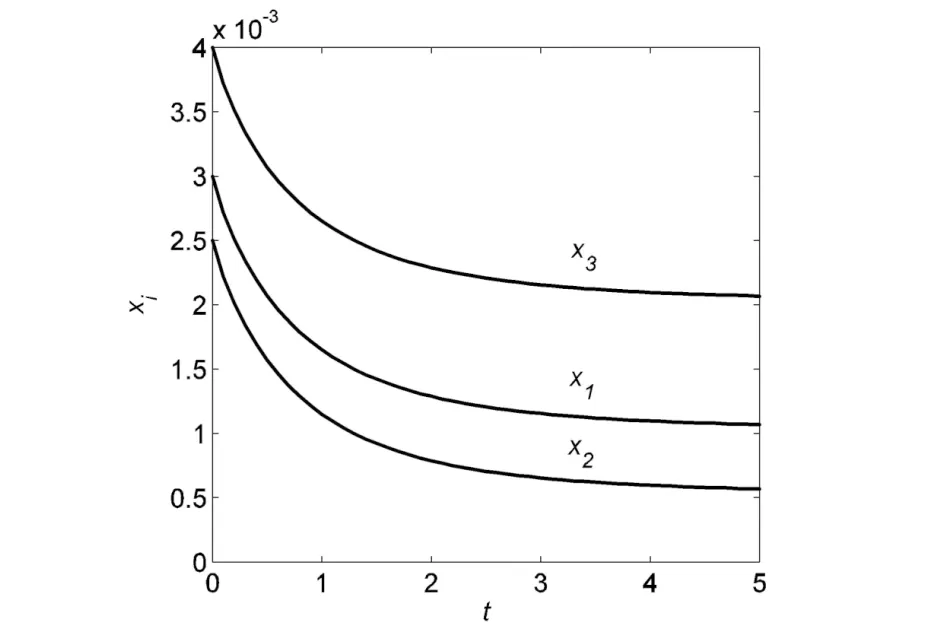
定义2[4]假设n∈Z+,x(t)∈Cm([0,+∞),Rn)且m-1<α 引理1[5]设m∈Z+且m-1<α 特别地,当p=q=2,则退化为Cauchy-Schwartz不等式,即: 引理3[6]假设σ<1且σ≠0.对于0 假设n为网络的神经元个数,x(t)=(x1(t),x2(t),…,xn(t))T表示t时刻的状态向量,fj和gj分别表示在t和t-τ时的激励函数,αi(xi(t))是放大函数,βi(xi(t))是行为函数,τ表示时滞,aij,bij分别表示连接权重,Ii表示第i个神经元的外部输入. 分数阶时滞Cohen-Grossberg神经网络可以用如下微分方程来描述: (1) 其中0<α<1,i=1,2,…,n. 记C([-τ,0],Rn)是定义在区间[-τ,0]上的全体n维连续向量函数的全体.系统(1)的初始条件为: x(t)=φ(t),t∈[-τ,0], (2) 假设系统(1)满足以下条件: (H3) 对于i=1,2,…,n,激励函数fj和gj满足Lipschitz条件,即:存在常数ξj>0和ηj>0满足|fj(x)-fj(y)|≤ξj|x-y|,|gj(x)-gj(y)|≤ηj|x-y|,∀x,y∈R; 引理5[8]假设条件(H1)~(H4)成立,则系统(1)存在唯一的平衡点. 定义3 假设条件(H1)~(H4)成立,δ和ε是两个任意正常数且δ<ε,x*是系统(1)的平衡点,x(t)为系统(1)满足条件(2)的一个解.如果‖φ-x*‖<δ,那么: ‖x(t)-x*‖<ε,∀t∈[0,T], 对于0<α≤0.5和0.5<α<1,以下分别给出系统(1)达到有限时间稳定的充分条件. 定理1假设条件(H1)~(H4)成立,给定两个任意正常数δ和ε,且δ<ε.当0.5<α<1时,若: 其中: 则系统(1)是有限时间稳定的. 证明假设x(t)=(x1(t),x2(t),…,xn(t))T是系统(1)的满足初始条件(2)的一个解,x*是系统(1)的平衡点,则有: 由Cauchy-Schwartz不等式得: ‖z(t)‖≤ 则有: ‖z(t)‖≤ 其中: 注意到t∈[-τ,0]且‖φ(0)‖≤‖φ‖=supθ∈[-τ,0]‖φ(θ)‖,则有: 从而: 令u0(t)=‖φ‖e-t+γ2‖φ‖,ω(t)=(γ1+γ2e-t),u(t)=e-t‖z(t)‖,v(t)=1,则由引理3和引理4得: W(t)=e-(γ1+γ2e-τ)2t, 所以: ‖z(t)‖e-t≤(‖φ‖e-t+γ2‖φ‖)+ (‖φ‖+γ2‖φ‖)2e(γ1+γ2e-τ)2t, 从而‖z(t)‖≤‖φ‖{1+γ2et+2(1+ γ2)e[(γ1+γ2e-τ)2+1]t}. 其中: 则系统(1)是有限时间稳定的. 定理3的证明与定理2的类似,在此从略. 在本节中,我们给出数值实验来证实主要结果的正确性. 考虑如下分数阶Cohen-Grossberg神经网络模型: (3) β1(x1)=1.25x1,β2(x2)=3x2,β3(x3)=2.5x3, a11=0.2,a12=0.1,a13=-0.1, a21=0.25,a22=-0.15,a23=-0.1, a31=-0.1,a32=0.1,a33=0.2, b11=-0.1,b12=0.1,b13=0.2, b21=0.15,b22=-0.15,b23=-0.1, b31=0.15,b32=-0.15,b33=0.25, I1=0.0012,I2=0.0015,I3=0.0050, fj(xj)=gj(xj)=0.02(|xj+1|-|xj-1|). 通过计算,可得: 从而系统(3)有唯一的平衡点x*,且满足如下方程组: 其中初值为x(t)=(0.003,0.0025,0.004)T,∀t∈[-0.1,0].取δ=0.01,ε=1,则系统(3)达到有限时间稳定的时间T=2.5824.图1展示了系统(3)的状态变量. 图1 系统的时间响应曲线Fig.1 Time response curve of the system 本文主要讨论了一类分数阶时滞Cohen-Grossberg神经网络的有限时间稳定性问题.首先,我们给出了一个系统平衡点存在且唯一的充分条件;然后,对于阶数在区间(0,0.5]和(0.5,1)内分别给出了一个保证系统有限时间稳定的充分条件.我们的证明方法主要是利用分数阶导数的性质、Hölder不等式和推广的Gronwall不等式.特别地,我们得到的充分条件是一些比较容易计算的代数不等式;最后,运用MATLAB仿真证实了主要结果的有效性.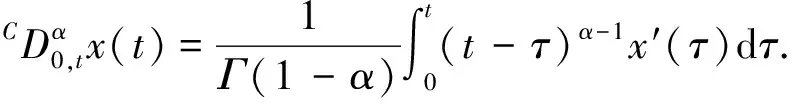
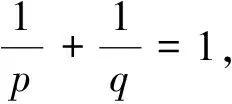
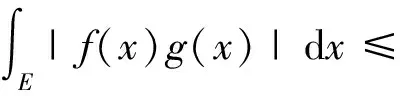
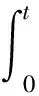


2 模型介绍
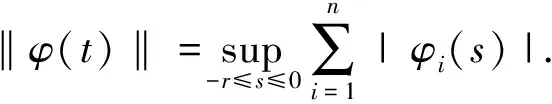
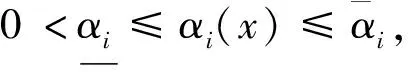
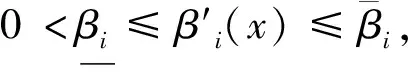
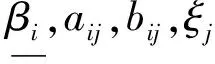
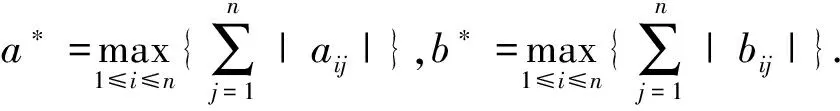
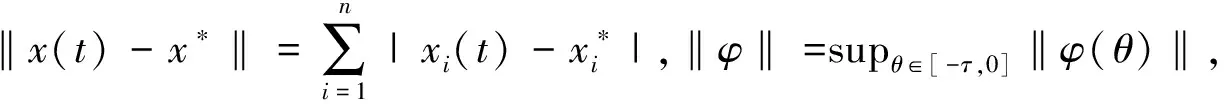
3 主要结果
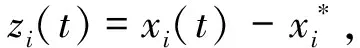




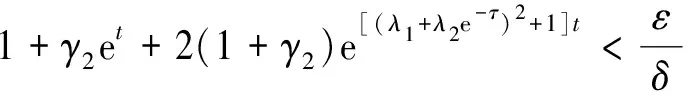
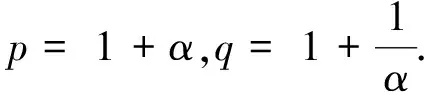
4 数值仿真
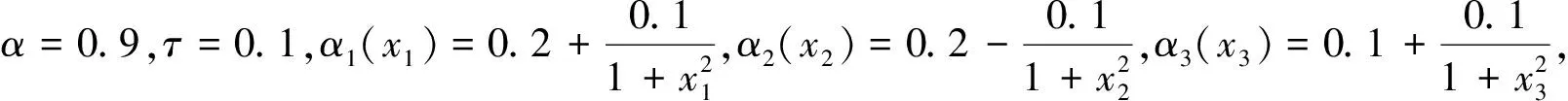
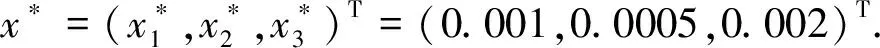
5 结论
