空间变化的彩色形态算子

段汕，周奇鱼，刘丹

(中南民族大学 数学与统计学学院，武汉 430074)

基于固定结构元素的二值与灰值数学形态学方法具有完整的理论体系和广泛的应用领域[1]. SERRA[1]提出的结构函数的思想将固定结构元素扩展到SV的形式，使得相应的形态算子在理论和方法上具备自适应性. BOUAYNAYA N和SCHONFELD D在文献[2,3]中详细阐述了SV灰值形态学的一般理论,通过引入SV结构函数，建立SV灰值形态腐蚀、膨胀、开、闭算子的基本形式，并研究了其相关性质，从理论和方法推广了固定结构元素下的灰值形态学理论.对于彩色图像或更一般的多值图像形态学方法的研究一直以来都是众多学者探索的目标.

将上述单值形态学理论扩展到彩色或多值图像，首先需要解决的是向量数据序关系以及与之相关的极大、极小运算的建立.在这一领域，本文以SV灰值形态学理论为基础，对SV彩色形态算子[4-6]进行了研究. 灰值图像表现为单值函数的形式，而彩色图像则是以向量函数的形式存在. 建立向量数据的序关系是研究彩色图像形态学方法的关键. 有关向量数据序关系的建立已有众多不同特点的方案[7-11]，如边缘序、条件序和P序，以及基于空间填充曲线[4]的导出序等方法. 本文将在SV灰值形态学理论[2]的基础上，通过引入双方单值的序函数，建立彩色图像模型空间上的导出序及与之相关的极大和极小运算，并以此为基础，建立SV彩色形态算子的框架理论，对SV彩色形态腐蚀、膨胀、开、闭算子的基本形式和形态学基本性质进行了研究推证. 研究表明，基于序函数的SV彩色形态算子，保留了SV灰值形态算子的基本性质，其研究结果为多值形态学框架理论的发展提供了基础.

1 SV灰值形态算子

BOUAYNAYA N和SCHONFELD D在文献[2,3]中对SV灰值形态算子进行了研究，给出了SV灰值形态基本算子的定义及等价形式,并建立了相关性质.

考虑欧氏空间E=Rn. 将灰值图像空间Ω={f:f=f(x)∈R,x∈Rn}中的图像f的支撑集记为：

Spt(f)={x∈E,f(x)≠-∞},

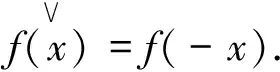
灰值图像的SV结构函数θ是一个从E|→U1的映射，其中U1是E上所有上半连续单值函数的全体.对任意的x∈E所对应的结构函数记为θx，且对u∈E,θx(u)∈R. 结构函数θ的转置定义为：

(1)

对于灰值图像f∈Ω，其四个基本的SV灰值形态腐蚀、膨胀、开、闭运算具有如下形式[2]：

εθ(f(x))=∧u∈Spt(θx)(f(u)-θx(u))=∨{v/θx+v≤f;v∈R},

(2)

(3)

Γθ(f)(x)=δθ(εθ(f(x)))=∨{θu+v≤f;(u,v)∈

E×R},

(4)

(5)

它们具有如下形态学性质：

性质1[2]设f,g∈Ω，则有：

(1)若f≤g，则εθ(f)≤εθ(g),δθ(f)≤δθ(g)(增性)；

(2)若θx(u)≥0，则δθ(f)≥f(扩展性)，εθ(f)≤f(非扩展性)；

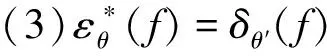
(4)δθ(f)≤g⟺f≤εθ(g)(附益性).

性质2[2]设f,g∈Ω，则有：

(1)若f≤g，则Γθ(f)≤Γθ(g),Φθ(f)≤Φθ(g)(增性)；

(2)Φθ(f)≥f(扩展性)，Γθ(f)≤f(非扩展性)；

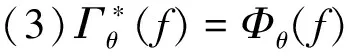
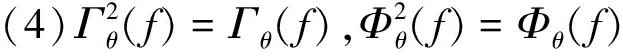
2 彩色图像空间

彩色图像表现为三维向量函数的形式：f(x)={f1(x),f2(x),f3(x)}，其中fk∈Ω,k=1,2,3.彩色图像f的支撑集记为[5]：

Supp(f)={x∈E,f1≠-∞,f2≠-∞,f3≠-∞}.

由灰值图像SV结构函数的定义，将彩色图像空间中的向量结构函数θ定义为E|→U3的映射，其中U3是E上的所有上半连续的三维向量函数的全体. 对任意的x∈E所对应的三维SV向量结构函数仍记为θx:

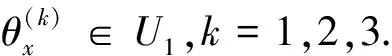
(6)

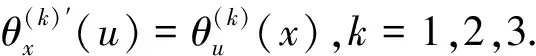
引入双方单值的序函数h:R3→R,x→h(x)，其将彩色图像中的每个像素点所对应的向量数据映射成为标量数据，利用实数集R上的序关系，可导出向量数据的序关系，称其为基于h的导出序，即对任意的xi,xj∈R3，

xi≤xj⟺h(xi)≤h(xj)⟺h-1(h(xi))≤

h-1(h(xj)),

显然，h关于向量及h-1关于标量均是增性的.

基于h的向量数据的极大和极小运算形式如下：

∧xi=h-1(∧h(xi));∨xi=h-1(∨h(xi)),

或：

h(∧xi)=(∧h(xi));h(∨xi)=(∨h(xi)),

即向量数据的极大极小运算与序函数h是可交换的.

利用基于h的导出序，可以建立彩色图像空间上的序关系:

f≤g⟺h(f)≤h(g)⟺f(x)≤g(x)⟺h(f(x))≤h(g(x)).

(7)

彩色图像空间在序关系(7)的基础上构成一完备格.

3 SV彩色形态算子

在SV灰值形态腐蚀、膨胀、开、闭运算的定义及等价形式的基础上，可建立基于序函数h的SV彩色形态腐蚀、膨胀、开、闭算子[5]：

εθ(f(x))=h-1[∧u∈Supph(θx)(h(f(u))-h(θx(u)))]=

h-1[∨u∈Supph(θx){α/(α+h(θx))≤h(f)}].

(8)

(9)

(10)

利用h函数，可得SV彩色形态开、闭算子Γθ，Φθ的等价形式：

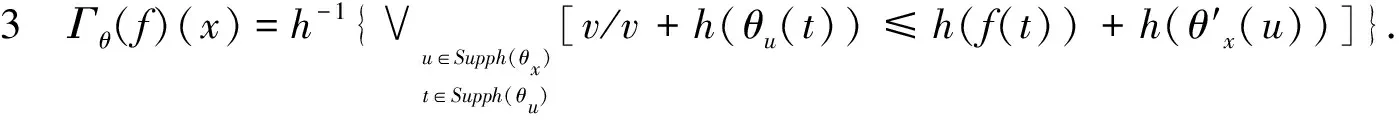
证明由(8)、(9)、(10)式可得:

Γθ(f)(x)=δθ(εθ(f(x)))=

h-1{∨u∈Supph(θx){(∨t∈Supph(θu){α/α+h(θx(t))≤

(11)

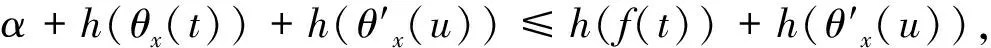
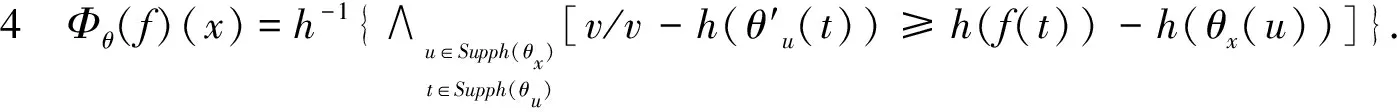
证明由闭算子的定义，得:

Φθ(f)(x)=εθ(δθ(f(x)))=

h(f(t))})-h(θx(u))},

(12)

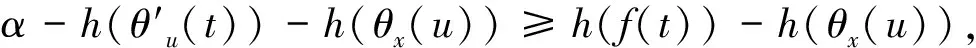
h(θx(u))]}.

在以上SV彩色形态腐蚀、膨胀、开、闭算子的定义及等价形式的基础上，可以进一步研究SV彩色形态算子的相关形态学性质.

4 SV彩色形态算子的基本性质

形态算子具有其基本的特点和性质，这些性质是实现形态算子功能的基本保证.以下对彩色图像空间上的SV彩色形态腐蚀、膨胀、开、闭算子的性质进行相关研究.

4.1 腐蚀和膨胀的性质

性质5(附益性)δθ(f)≤g⟺f≤εθ(g).

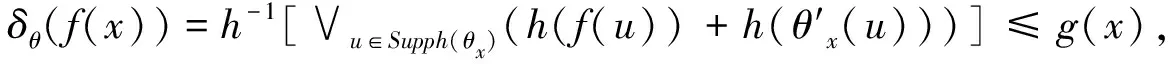
f(u)≤h-1[∧x∈E(h(g(x))-h(θu(x)))]，由此可得f(u)≤εθ(g(u)),即f≤εθ(g).

由此性质可见SV彩色形态腐蚀和膨胀具有附益性，是一对附益算子.

性质6(增性)若f≤g，则εθ(f)≤εθ(g)；δθ(f)≤δθ(g).

证明1)由(7)式可知：对任意的u∈E，有h(f(u))≤h(g(u)) ，可得：

h(f(u))-h(θx(u))≤h(g(u))-h(θx(u)),故∧u(h(f(u))-h(θx(u)))≤∧u(h(g(u))-h(θx(u))),即h-1(∧u(h(f(u))-h(θx(u))))≤h-1(∧u(h(g(u))-h(θx(u)))),从而εθ(f(x))≤εθ(g(x)).

2)由(7)式可得，对任意的u∈E，h(f(u))≤h(g(u)),可以得出：

该性质表明SV彩色形态腐蚀和膨胀关于目标对象都是增性算子.

性质7(扩展性、非扩展性)如果h(θ)≥0，则有δθ(f)≥f;εθ(f)≤f.

证明1)由h(θ)≥0,则：

εθ(f(x))=h-1[∧u∈Supph(θx)(h(f(u))-h(θx(u)))]≤

h-1[h(f(u))-h(θx(u))]≤h-1(h(f(x)))=f(x).

2)由(2)式，当h(θ)≥0时，有h(θ′)≥0,则：

此性质说明在序函数h具有非负性的前提下，SV彩色形态腐蚀具有非扩展性，SV彩色形态膨胀具有扩展性.

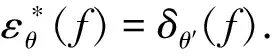
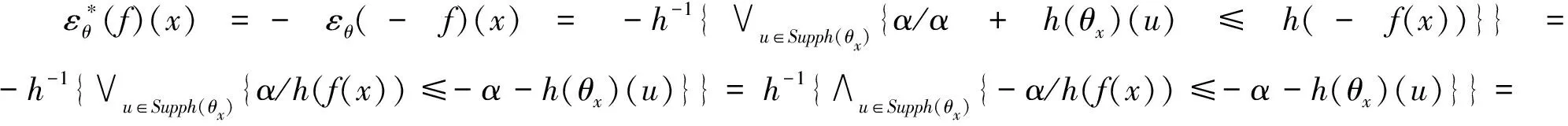
δθ′(f).

该性质表明，在序函数h具有奇性的条件下，SV彩色形态腐蚀与膨胀是一对对偶算子.

基于h变换的SV向量结构函数的θ1，θ2序关系，具有如下形式：

θ1≤θ2⟺(θ1)x≤(θ2)x⟺h((θ1)x(u))≤h((θ2)x(u)),x,u∈E.

性质9(结构元素的增性)若θ1≤θ2，则εθ2(f)≤εθ1(f);δθ1(f)≤δθ2(f).

证明1)由θ1≤θ2，则对任意的α∈R及x,u∈E，有：

h((θ1)x(u))+α≤h((θ2)x(u))+α,

故对于f(x)∈U3，则有:

{α/h((θ2)x(u))+α≤h(f(u))}⊆{α/h((θ1)x(u))+α≤h(f(u))}，从而：

∨u∈Supph(θx){α/h((θ2)x(u))+α≤h(f(u))}≤

∨u∈Supph(θx){α/h((θ1)x(u))+α≤h(f(u))},

即：

h-1{∨u∈Supph(θx){α/h((θ2)x(u))+α≤h(f(u))}}≤h-1{∨u∈Supph(θx){α/h((θ1)x(u))+α≤h(f(u))}},

故εθ2(f(x))≤εθ1(f(x))；

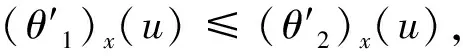
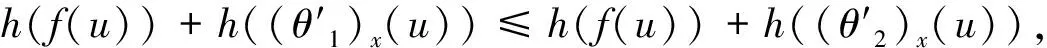
故：

即δθ1(f)≤δθ2(f).

这个性质说明SV彩色形态学腐蚀和膨胀关于动态结构元θ分别是减性和增性的.

给定两个结构向量函数映射θ1和θ2，我们用εθ1(θ2)和δθ1(θ2)来表示结构向量函数映射的腐蚀和膨胀，即对任意的x∈E，εθ1(θ2)(x)=εθ1(θ2(x))和δθ1(θ2)(x)=δθ1(θ2(x))，则有如下关系成立：

性质10(结构元素的复合性)εθ2[εθ1(f)]=εδθ1(θ2)(f),δθ2[δθ1(f)]=δδθ2(θ1)(f).

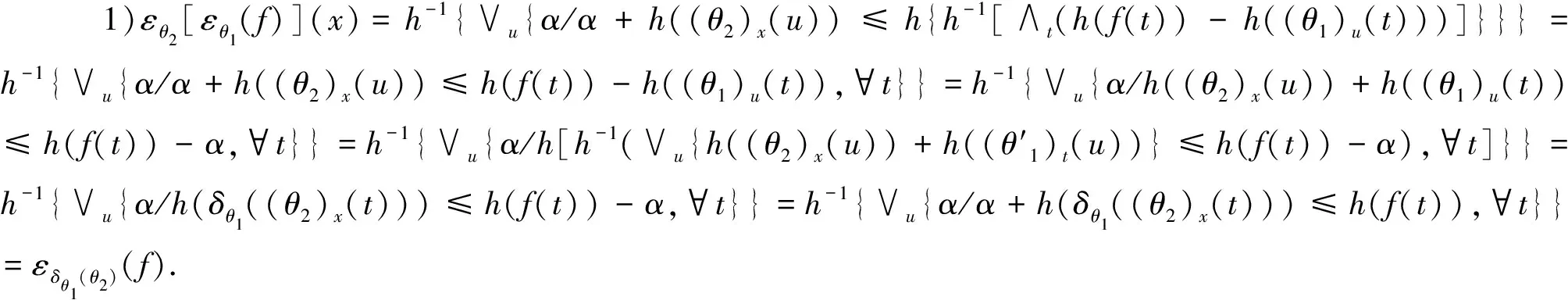
此性质表明用不同结构元对SV彩色图像进行连续腐蚀(膨胀)可转化为对结构元进行连续膨胀(腐蚀)之后再腐蚀(膨胀).

4.2 开和闭的性质

性质11(增性)若f≤g，则Γθ(f)≤Γθ(g);Φθ(f)≤Φθ(g).

证明1)由性质6可得：f(x)≤g(x)，则εθ(f)(x)≤εθ(g)(x)，从而可得：

δθ(εθ(f(x)))≤δθ(εθ(g(x))),

即Γθ(f)≤Γθ(g).

2)由膨胀的增性可知，对任意的x∈E，有δθ(f(x))≤δθ(g(x))，由性质6腐蚀的增性可得：

εθ(δθ(f(x)))≤εθ(δθ(g(x))),

从而得Φθ(f)≤Φθ(g).

该性质说明SV彩色形态学增性算子的复合仍是增性算子.

性质12(扩展性、非扩展性)Γθ(f)≤f;Φθ(f)≥f.

证明1)由性质3可知：

即Γθ(f)≤f.

2)又由性质4可知：

即Φθ(f(x))≥f(x).

此性质说明SV彩色形态开具有非扩展性，SV彩色形态闭具有扩展性.

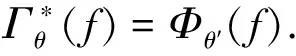
证明由性质8可得：

该性质表明SV彩色形态开、闭运算是一对对偶算子.

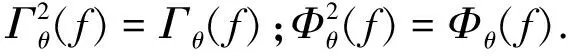
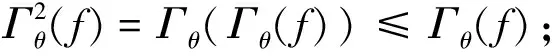
Γθ(f)(x)=δθ(εθ(f(x)))≤f(x),

即δθ(εθ(δθ(f(x))))≤δθ(f(x)),

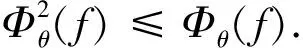
该性质说明SV彩色形态开、闭算子都是幂等算子.

由以上这些性质可以看出，基于h变换下所给出的SV彩色形态腐蚀、膨胀以及开、闭算子与SV灰值形态学理论在性质上基本保持一致.

5 结语

本文在文献[5]中所表示的SV彩色形态学腐蚀、膨胀的基础上，借助文献[2]中的SV灰值形态学理论，对SV彩色形态基本算子的理论进行深入研究，并探讨了腐蚀、膨胀、开、闭这四种算子的相关性质.通过以上研究，可以清晰地看到，SV彩色形态算子和SV灰值形态算子在大多数性质上基本保持一致，但SV彩色形态算子的核表示有待进一步研究.本工作实现了从SV灰值形态算子到SV彩色形态算子研究的扩展,有助于深入地理解SV彩色形态算子，以及整个数学形态学的基本理论，为后续的研究奠定了理论基础.