单晶炉观察窗工作热应力模拟

高利强

(西安理工大学工程训练中心，西安 710048)

1 引 言

提拉法单晶炉是单晶体Cz法生长设备。其炉室通常由炉底、炉筒、炉盖等焊接件装配而成，也存在其他装配形式如炉体和炉门装配成一体。这些焊接件在焊接过程中加热和冷却循环不可避免地产生焊接热应力热应变循环,导致残余应力的产生。在此过程中焊接接头可能产生焊接热裂纹、焊接冷裂纹、层状撕裂等焊接缺陷。经过振动时效处理，降低和均化焊接应力后，焊件还要进行一系列冷加工过程，然后进行冷炉和煅烧检验。在冷炉检验中如果出现冷却水泄漏，说明存在上述某种裂纹。在煅烧或拉晶过程中，炉室及炉壁分布着静态或动态的热场，从而使炉室内表面温度最高达到300 ℃左右。这必然导致组焊件出现热应力，为区别焊接残余应力，把单晶炉工作时的情况不妨称作工作热应力。这样，残余热应力和工作热应力的共同作用又可能引起焊接件产生再热裂纹、应力腐蚀裂纹、冷裂纹等焊接缺陷，会导致炉室工作时发生冷却水泄漏事故，损坏室内系统(包括坩埚、晶体材料、加热系统和保温罩等)。金属断裂理论认为裂纹的形核和迅速扩展跟拉应力有关，很多文献研究过应力对再热裂纹、应力腐蚀裂纹等缺陷产生机理的影响，认为除了拉应力，也和压应力有关，它们都是跟实验方法紧密相关的应力矢量，综合两种观点以基于应力张量的冯米斯等效应力作为衡量标准，应最大限度地消除应力集中和减少高应力区，以防止出现裂纹或断裂，避免漏水事故。生产实践发现冷却水泄漏事故主要发生在炉盖观察窗焊缝处，而且在相同的焊接材料和焊接工艺条件下，其漏水与焊件结构形状有一定关系。下面将对观察窗焊缝的工作热应力进行数值模拟，试图从理论上找出冷却水泄漏和焊件形状等因素之间的关系。

2 有限元模型

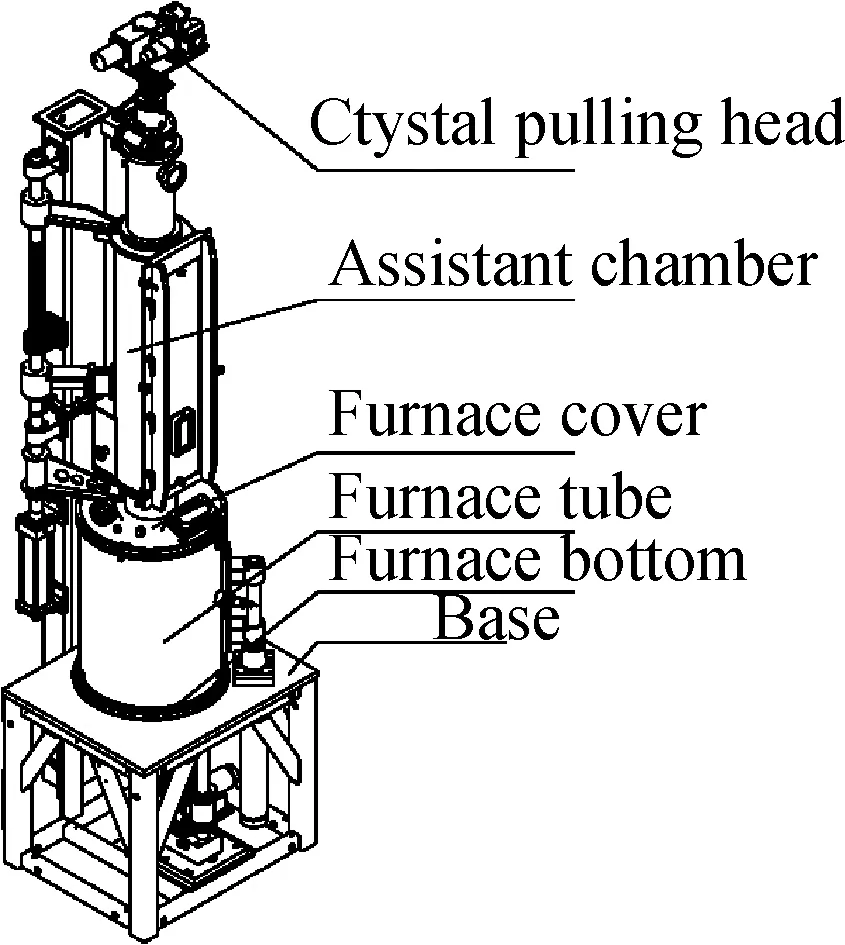
图1 提拉法单晶炉主机Fig.1 Main machine of Czochralski single crystal furnace

图1示出了一种电阻型提拉法经典炉型的主机结构。它包含了通常所需的几个部件，底座及坩埚传动、炉室、副室、晶体提拉头等。其特征是炉室内采用筒状石墨电阻加热元件。该热系统和水、氩气冷却系统共同作用，维持着晶体生长在固体、熔体两种形态下所需的温度梯度。在熔料和晶体生长过程中，由于不断发生物相转化，温度分布实时变化处于动态，在热系统保温盖和保温罩内部其变化较明显，而外部炉壁的温场变化微弱，一定情况下，可近似为静态。

要计算热应力首先计算热场，然后把求出或确定的温度作为载荷，其与炉盖受到其它的约束条件一起可用来建立有限元方程，求解后就得到了工作热应力。

图中炉盖支撑着上面部件即副室和晶体提拉头，受到它们的重力。炉筒又支撑着炉盖，对其下端面施加了一个位移边界条件。

照此情况可建立如下有限元模型。

2.1 几何模型

如图2～5所示，图2和图4(a)组合当m=181 mm,n=70 mm,M=225 mm,N=114 mm时，水夹层内外壁(近似为薄板的中面，以下同)横截面呈双矩形，模型用Plane-double rectangles表示，简记P-DRE；图2和图4(a)组合当m=n=70 mm,M=N=114 mm时, 水夹层内外壁横截面呈双正方形，模型用Plane-double squares表示，简记P-DSQ。

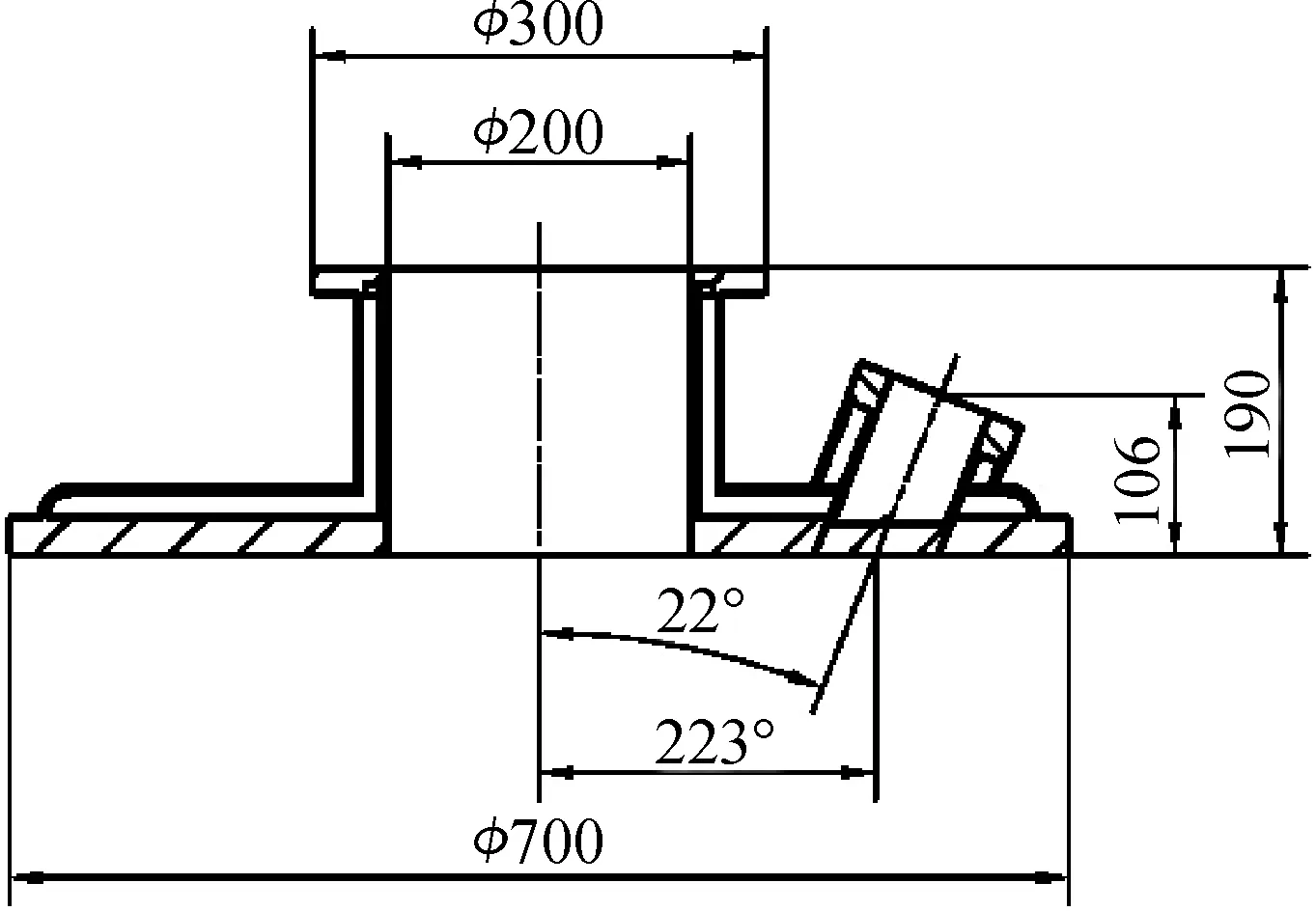
图2 平面炉盖几何模型Fig.2 Geometric model of planar furnace cover

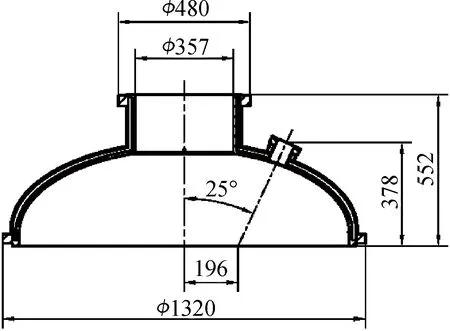
图3 椭圆炉盖几何模型Fig.3 Geometric model of elliptical furnace cover

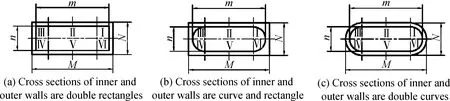
图4 观察窗形状模型Fig.4 Shape model of observation window

类似的对应关系如表1、2。其中，壁板带圆弧的长条窗横截面整体上视为曲线，以区别于圆形截面。

表1 平面封头窗形简称Table 1 Abbreviation for window shape of planar head

表2 椭圆封头窗形简称Table 2 Abbreviation for window shape of elliptical head

如图5所示：观察窗焊接接头漏水事故一般只出现在内壁，其上施焊时开放无遮挡、操作空间较充裕的一侧约定为第一焊缝或主焊缝，反之则称为第二焊缝或副焊缝，此时需要把外壁分成数块最后合装起来焊为一体。以下提到焊缝时，若无特殊说明均指内壁部位。

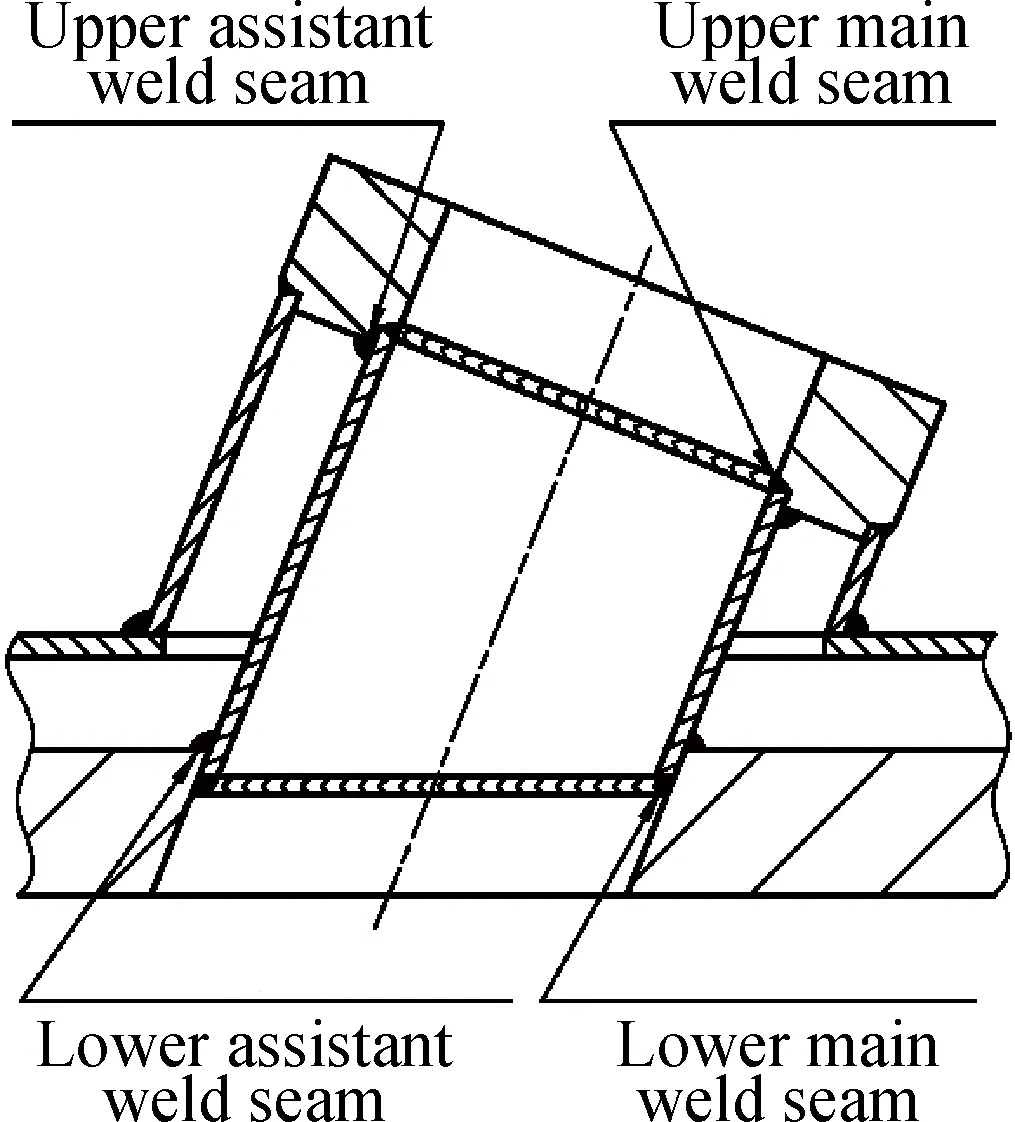
图5 观察窗焊接模型Fig.5 Welding model of observation window

2.2 材料模型

目前，国产设备炉室组焊件母材均为不锈钢材料304L，假定选用的焊条其化学成分同母材相同，这样炉盖内外壁和窗口内外壁及其焊缝计算时采用同样的物性参数，可通过下述办法确定。

不锈钢本构关系是非线性的，常采用Ranberg-Osgood模型，后经Hill修正和Van der Merwe[1]补充研究可表述为：

(1)

n=ln20/ln(σ0.2/σ0.01)

(2)

式中，E0为材料初始弹性模量，n为应变硬化指数，σ0.2为条件屈服极限即残余应变等于0.2%时的应力，σ0.01为规定比例极限即残余应变等于0.01%时的应力。参考相关文献对国产304不锈钢力学性能试验研究，含碳量更低的304L不妨取n值等于5, 于是得到：

(3)

表3给出了304L不锈钢不同温度时物性参数，其中20 ℃时的数值直接借用，290 ℃时可以通过线性插值得到近似值。例如，20 ℃、290 ℃时屈服强度分别为240 MPa、189 MPa，其它参数如表3所示。

表3 304L的物性参数[2]Table 3 Physical property values of 304L[2]

Ranberg-Osgood模型属于弹塑性力学模型。用20 ℃、290 ℃时的屈服强度替换公式(3)中σ0.2，用表3中弹性模量替换公式(3)中E0可得到公式(4)、(5)：

(4)

(5)

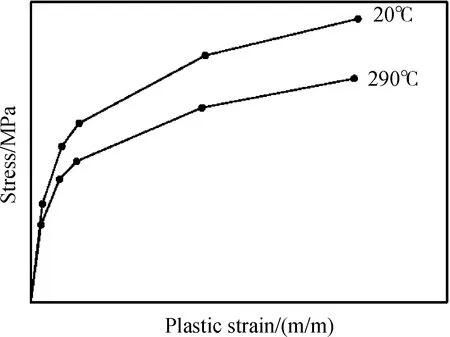
图6 本构模型Fig.6 Constitutive model

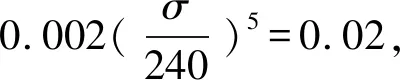
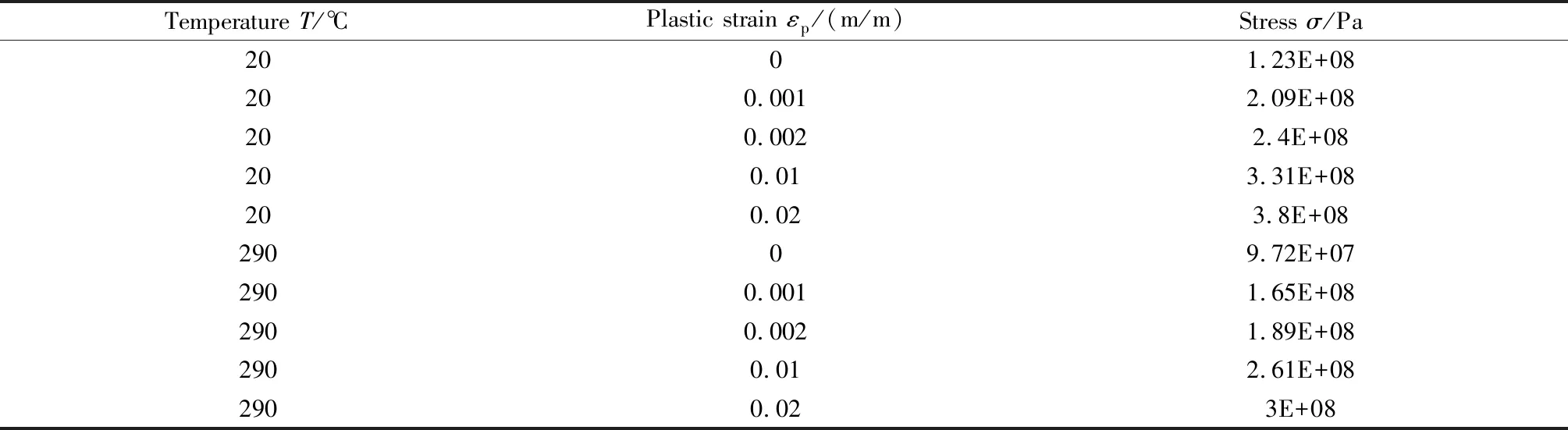
表4 物性参数Table 4 Physical property values

2.3 数学模型

2.3.1 稳态热传导一般形式

三维稳态温度场的场变量φ(x,y,z)在直角坐标中热传导方程一般形式为：

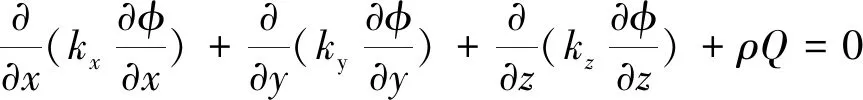
(6)

边界条件是

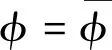
(在Γ1边界上)

(在Γ2边界上)

(在Γ3边界上)

2.3.2 稳态热传导具体参数

对晶体生长的模拟[3-7]，尽可能得到精确的数值解，需要考虑因素很多，普遍采用第二、三类边界条件。生长设备制造业关注目标是炉室外围具有水夹层的炉壁，为简便分析其炉盖组件观察窗形状对热应力的影响，兹忽略晶体生长过程的自然边界条件，只取炉盖焊接件(包含一个观察窗)作为研究对象，把各种换热综合作用的最终效果，根据经验和有关文献设定为强制条件，即第一类边界条件。当然，实际呈现的结果肯定是一个与时间相关的分布函数，这里简化处理，按区域设定为常数。

提拉法硅单晶炉的工作过程包括一天左右的拉晶过程和若干时间的冷却过程，然后取出单晶锭，这个周期类似对炉室内壁施行了一次低温时效。然而经冲压或卷制形成大比例弹性变形的奥氏体不锈钢构件不宜进行300～450 ℃的低温时效处理[8],所以炉室内壁的温度应控制在300 ℃以下，通过冷却水流量和流速可以实现。炉室外壁处在室内工作环境下，一般可以控制室温维持在25 ℃上下。生产实践当中水夹层的水温一般在50 ℃上下，所以求温场时，假定炉盖及其窗口内壁表面各处温度为290 ℃,假定外壁表面施加边界条件25 ℃,水夹层所有平面和曲面施加边界条件50 ℃。

2.3.3 弹塑性力学一般形式

弹塑性力学基本方程一般形式为：

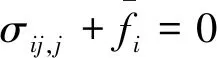
(7)

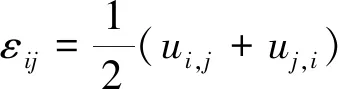
(8)

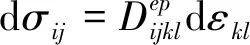
(9)

或

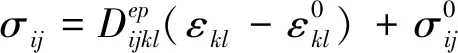
(10)

边界条件

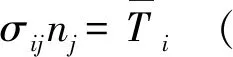
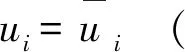
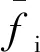
2.3.4 弹塑性力学具体参数

由图1看出，炉盖下面的炉筒支撑着它，考虑到它们随着室内温度同时热胀冷缩，认为炉盖下端面作用着一个无摩擦支撑，此即位移边界条件，在图2中Su为φ622 mm×φ700 mm的圆环，在图3中Su为最下面凸缘端面。炉盖上端面需要承受副室和晶体旋转提升部件的重力，此即分布力边界条件，Sσ在图2、3中分别作用3440 N、10535 N。炉盖受到的载荷包括自身重力(属于体力)、以及由温场产生的初应力和初应变。

3 计算结果与分析

热传导方程离散后建立有限元方程,据此求出稳态温度场后，它产生温度应变，从而在弹塑性力学的有限元方程中产生温度应变引起的载荷项，就可以进一步求出弹塑性体各部分的热应力。兹采用Ansys有限元分析软件完成离散求解过程。图7示出了椭圆封头上内外壁横截面均为曲线的长条孔即E-DCU观察窗子模型、上焊缝、上焊缝各区域等效热应力分布云图，类似得到各种窗形对应云图，限于篇幅不再示出，仅把最大应力列于表5和表6中。为便于观察，将表中整体焊缝最大应力示于图8～11。提取双面焊情况两种封头六种窗形沿主焊缝三条棱边路径等效热应力分布曲线如图12、13。提取两种封头三种长条窗形沿主焊缝三条棱边路径在单、双面焊情况等效热应力分布曲线如图14所示。

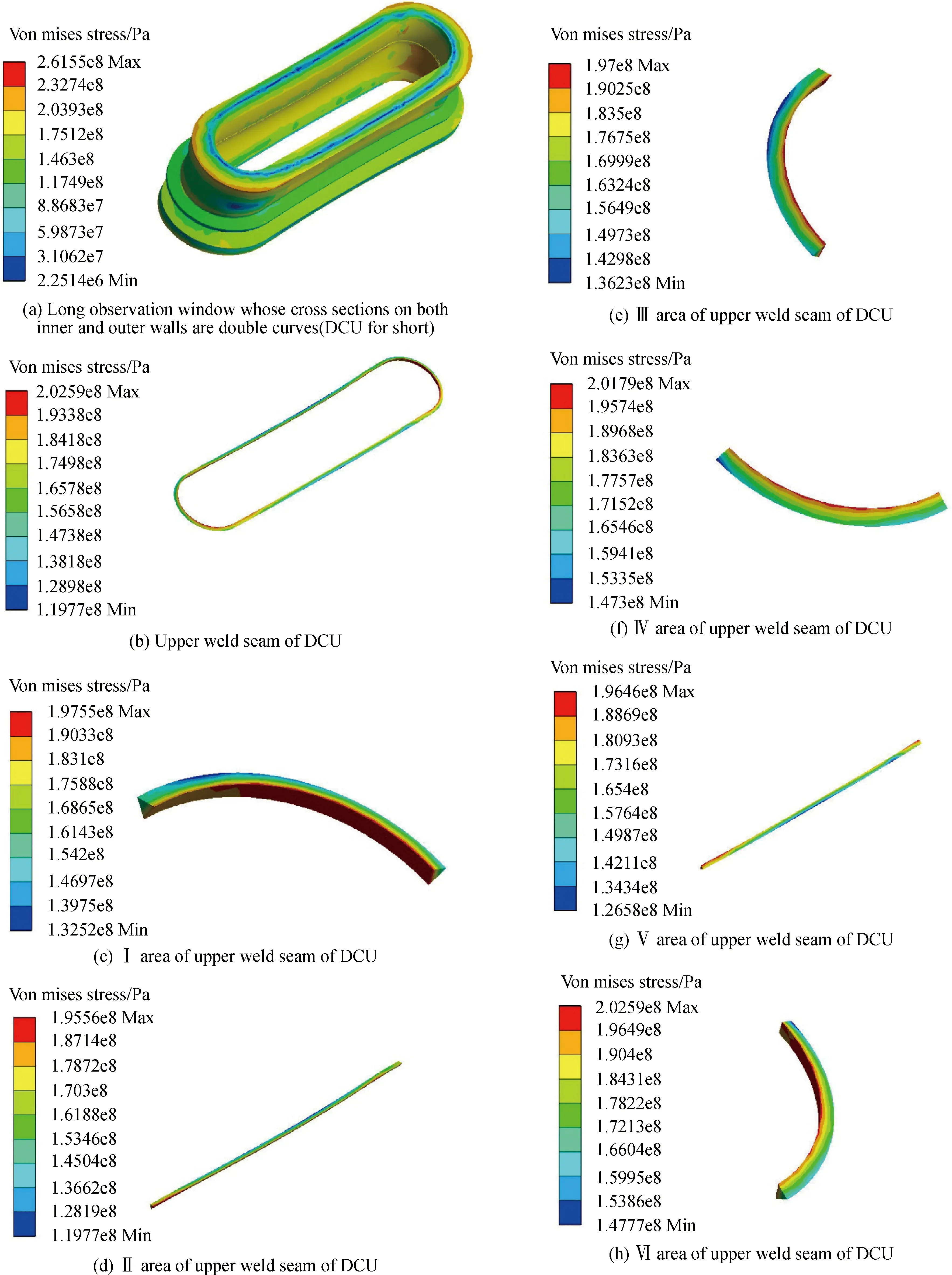
图7 子模型及上焊缝各区域热应力分布Fig.7 Thermal stress distribution in submodel and each area of upper weld seam

(1)图8、10表明两种封头的观察窗上下焊缝都在DSQ或DRE窗形取应力最大值，表5、表6说明焊缝各个区域绝大多数服从这个规律，例外情况发生在某些Ⅱ区和Ⅴ区的直线部分如表中上焊缝，这从路径分布曲线图12中也能看出来，曲线和云图两种类型的结果是一致的。手工焊接时，焊接质量是焊缝腐蚀漏水的关键原因，幸运的是直线部分的焊接质量很容易保证，不容易出现焊接缺陷，从而使裂纹扩展的临界应力大幅提高，即这两个区域韧性相对优良，综合考虑，不宜采用这两种窗形，同时圆形结构焊缝质量较容易保证，矩形结构很难保证，从工艺上也支持这种选项。

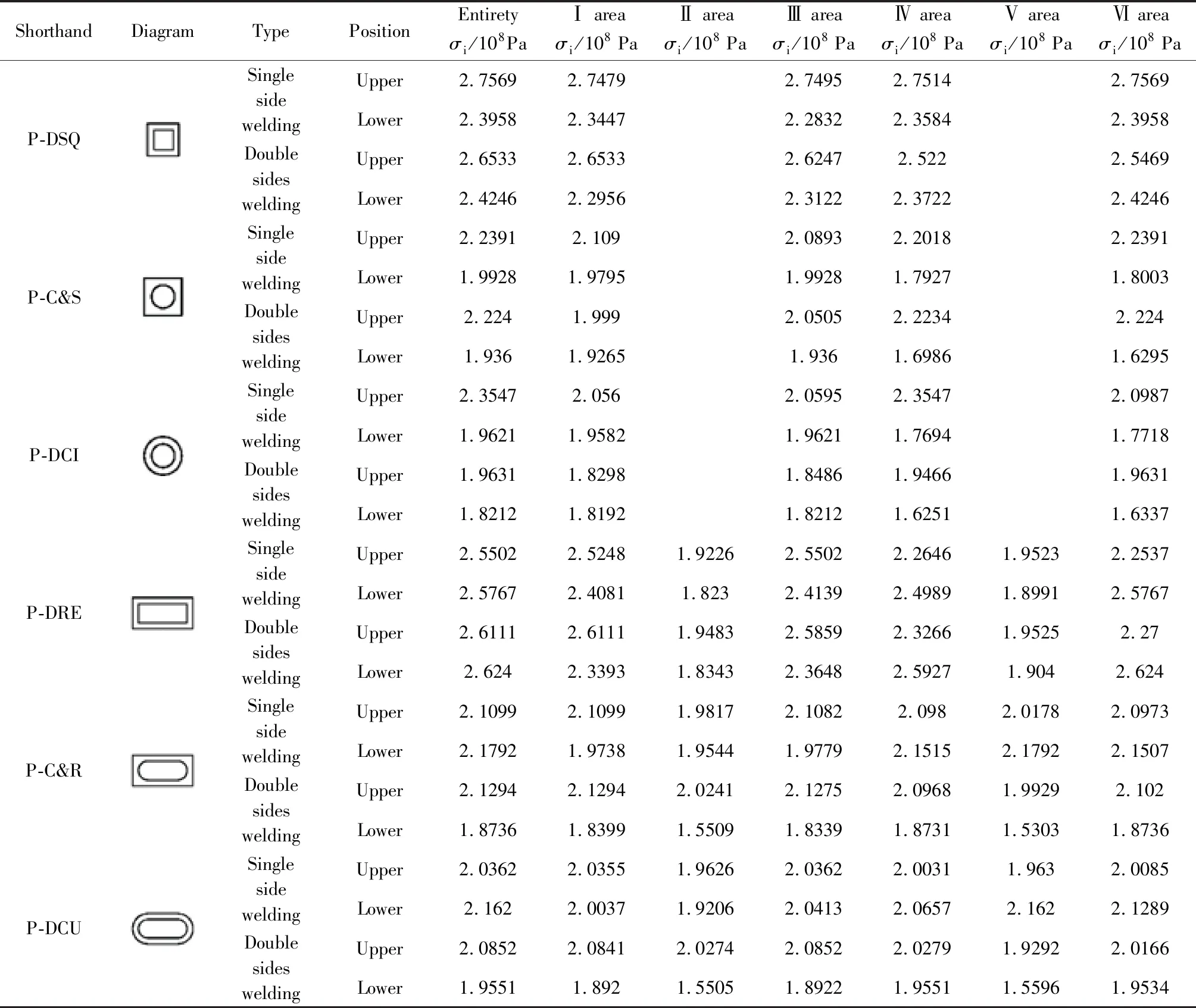
表5 平面封头窗形-主焊缝最大应力Table 5 Window shape of planar head-Maximum stress of main weld seam

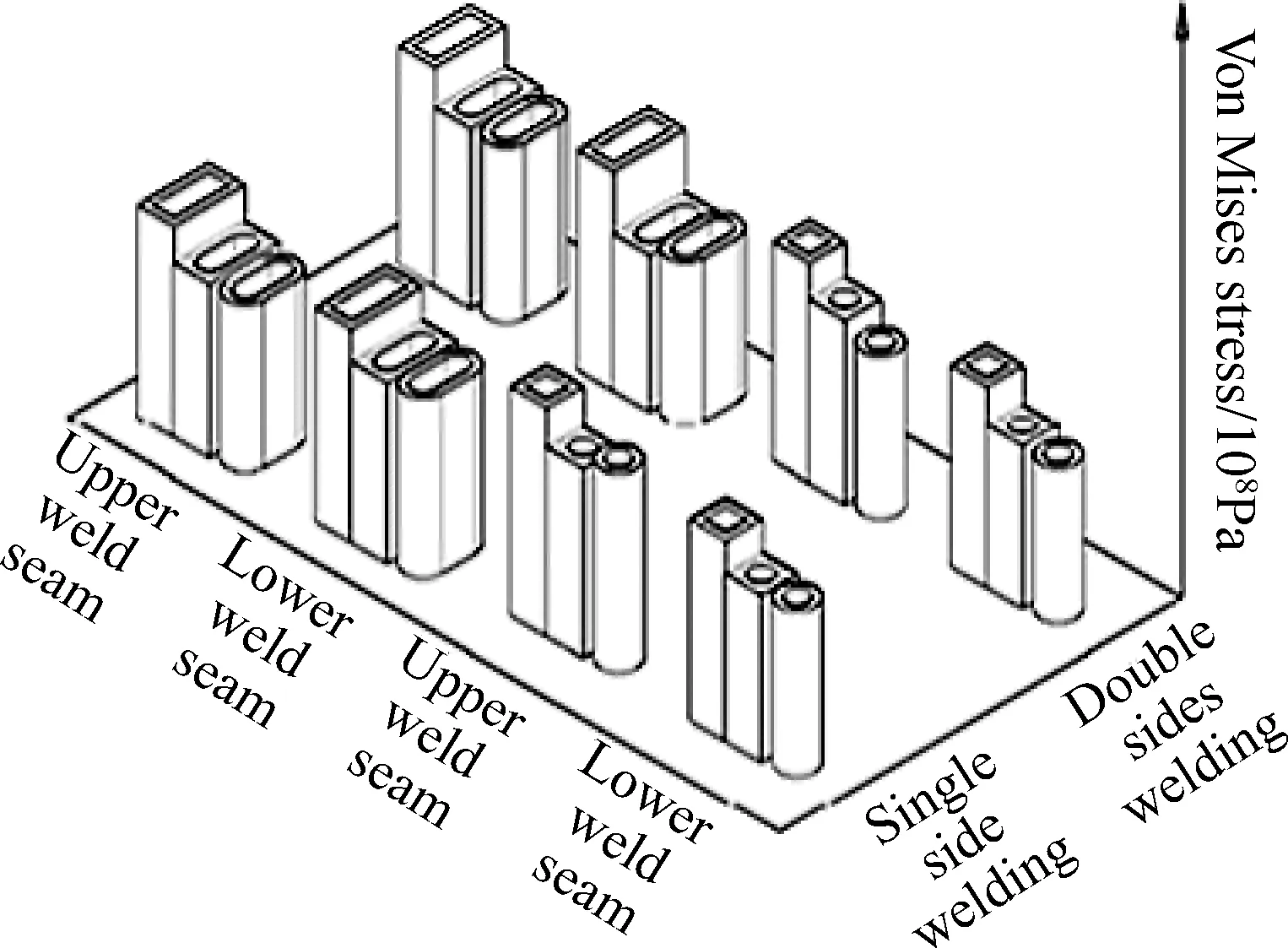
图8 平面封头窗口主焊缝最大应力/窗形影响Fig.8 Maximum stress in main weld seam of planar head window/effect of window shape

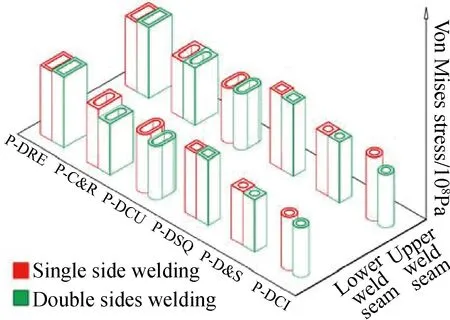
图9 平面封头窗口主焊缝最大应力/单双面焊接影响Fig.9 Maximum stress in main weld seam of planar head window/effect of single-sided and double-sided welding

图9、11表明双面焊几乎不影响主焊缝的应力分布，表5、6确认其各个区域服从此规律，这从路径分布曲线图14也能看出。

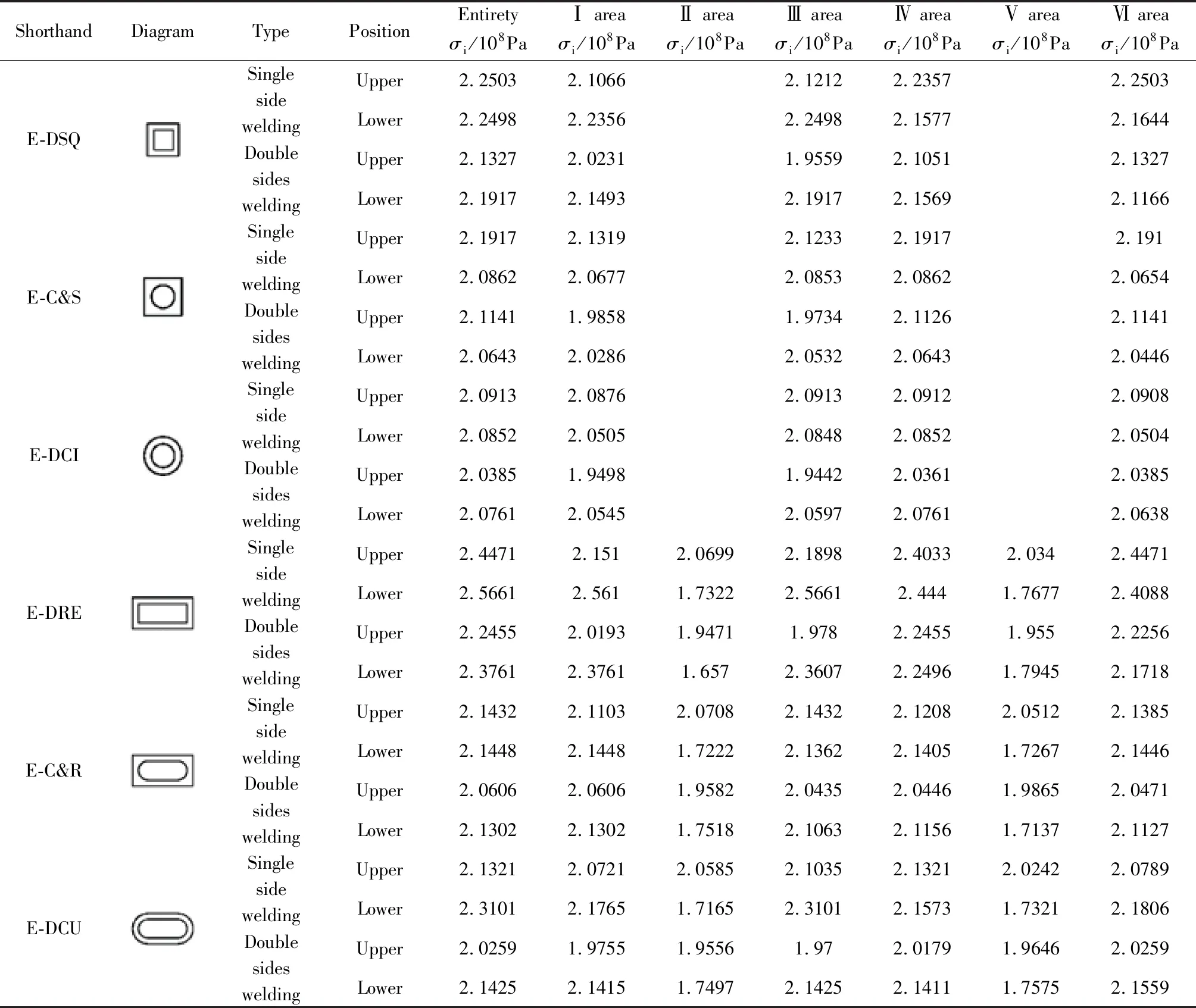
表6 椭圆封头窗形-主焊缝最大应力Table 6 Window shape of Elliptical head-Maximum stress of main weld seam

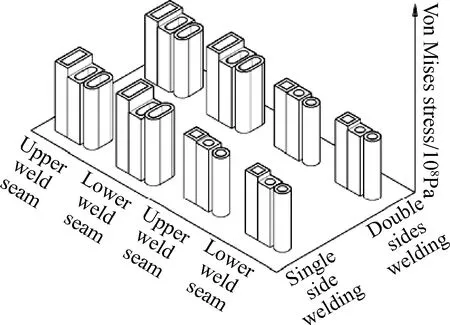
图10 椭面封头窗口主焊缝最大应力/窗形影响Fig.10 Maximum stress in main weld seam of Elliptical head window/effect of window shape

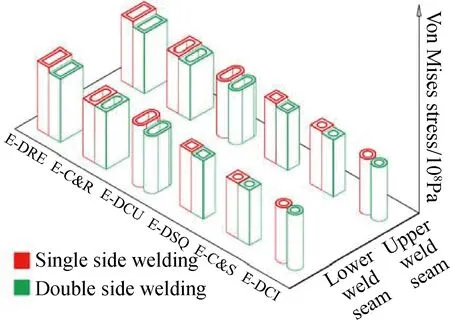
图11 椭圆封头窗口主焊缝最大应力/单双面焊接影响Fig.11 Maximum stress in main weld seam of Elliptical head window/effect of single-sided and double-sided welding

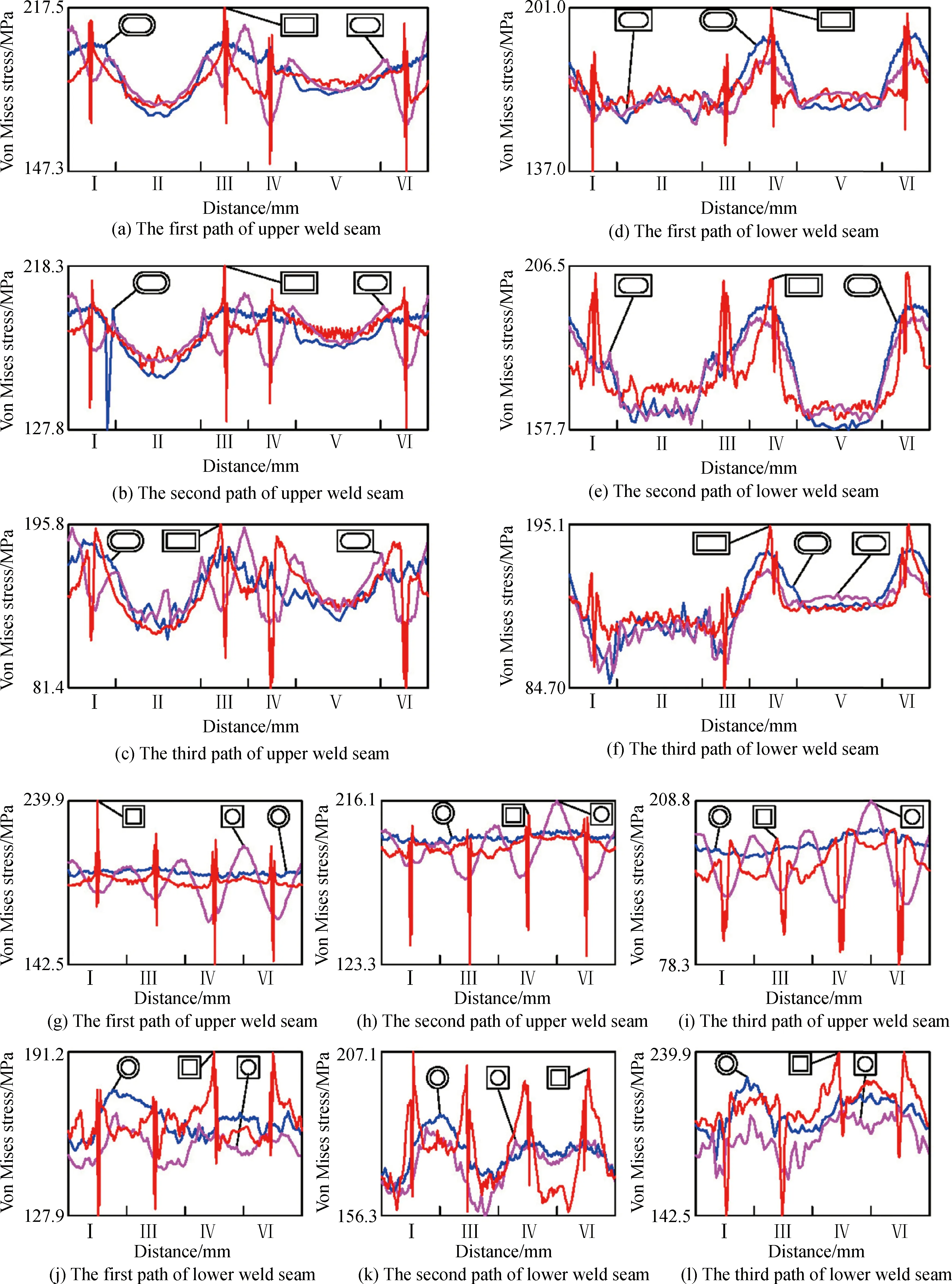
图12 平面封头窗口主焊缝沿路径热应力分布Fig.12 Thermal stress distribution along path of main weld seam in planar head window

(2)从图12、13看到，在焊缝一周范围内，沿每条路径应力成波浪式变化，各个半周区域内，应力分布是近似对称的，这是因为观察窗沿炉盖周向以轴线所在平面镜像对称。同一种窗形每条焊缝三棱边路径上应力分布曲线是相似的，那么组成焊缝的无数条路径也与它们相似，集成后将成为一个曲带，变化规律与单条路径相同。这说明通过三棱边路径可以预测焊缝区应力分布规律，例如从图12、13发现除Ⅱ、Ⅴ区外，最大应力都出现在DSQ或DRE窗形，与前面体积云图得到的结果一致。由于焊缝边界处在焊缝区和近缝区之间与两者都很近，那么三棱边路径也应该接近或代表近缝区的情况，换句话说，用焊缝几何边界(以区别于熔合线)3条棱边路径展示应力曲线，可以预测焊接接头一周范围内的分布规律。不同窗形在相似位置的路径上其应力曲线有相似性即总体变化趋势相同，还有显著区别即变化剧烈程度不同，使它们不能融合为一条线，而成不同程度分散交叉。DRE和DSQ窗形的应力曲线变化最剧烈，其它较为平缓，平面封头DCI窗形上焊缝3条路径的应力分布接近一条直线，明显比C&S和DSQ的波峰小如图12(g,h,i)。由此可以判断图中曲线的尖锐波峰部位出现应力集中现象，在绝大多数情况下，内外壁含直角的DRE和DSQ最严重，它们的焊缝在一周范围或各个区域内应力最大，这提示设计观察窗时，应略去它们的形状，而采用表1、2其它窗形。工程实践中，窗口内外壁横截面均设计为矩形(DRE)，主要归因于机加工艺简单，如果壁板带圆弧，相配合的窗口法兰要加工出外圆弧，用普通铣床难度大。

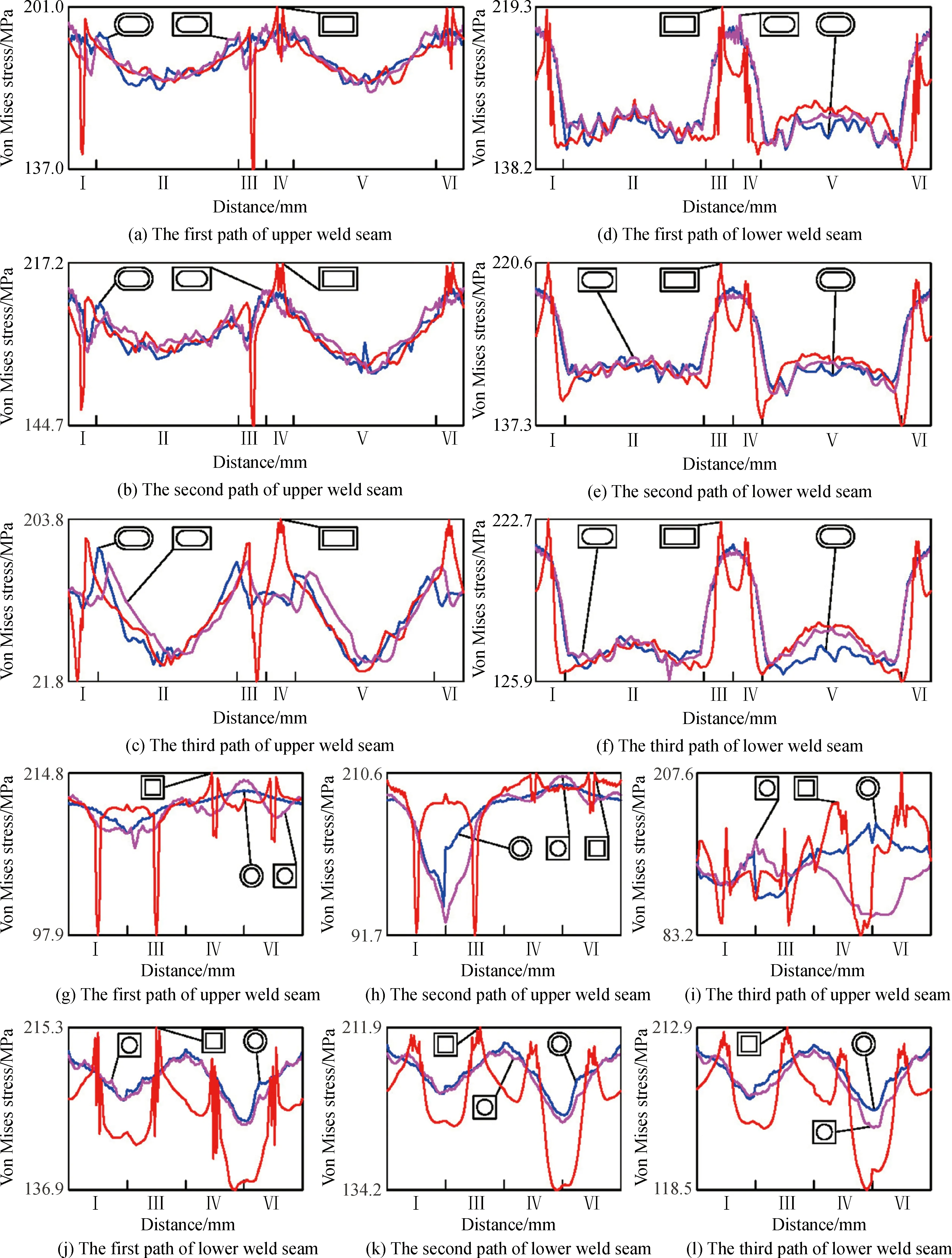
图13 椭圆封头窗口主焊缝沿路径热应力分布Fig.13 Thermal stress distribution along path of main weld seam in Elliptical head window

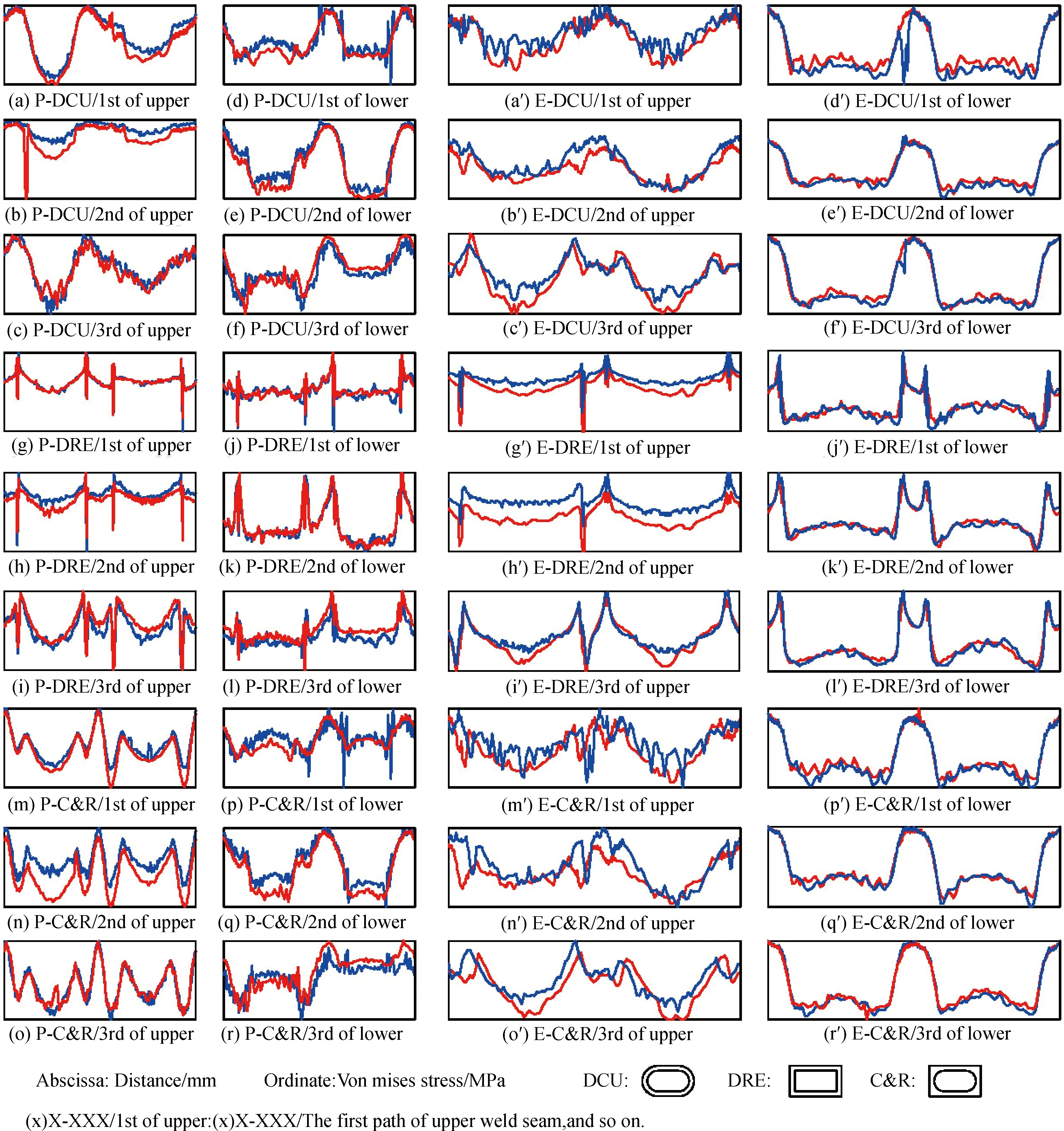
图14 双面焊与单面焊时主焊缝热应力分布比较Fig.14 Comparison of thermal stress distribution of main welding bead between double-sided welding and single-sided welding

壁板含正方形的DSQ和C&S在机加工艺和焊接质量等方面都比圆形窗DCI差，使方圆形观察窗多数情况下都用DCI窗形。模拟时列举前两者数据，为了说明从长条窗口变化到它们的特例方圆窗口时热应力影响服从相同规律，那么两个极限窗口中间所有尺寸，这一连续区域的长条观察窗也能服从。在模拟结果指引下，长条观察窗需要优化设计成C&R或DCU，通过使用夹具、模具和数控机床等克服制造工艺难度。目前，C&R在平面封头上用得较多，例如T50B、T62A、B、C、D、E系列单晶炉，DCU在椭圆封头上用得较多，例如T80、T70、T90、T100和T120等炉型。从同一条路径的不同区域看，有些应力大，有些较小，这种规律指出焊接过程更需关注的部位。比如，图12(d,f,j,l)Ⅳ、Ⅵ区，图13(d,e,f)Ⅰ、Ⅲ、Ⅳ、Ⅵ区应力较大，需给予更多关注。对热应力大小在整个路径范围内变化均衡的焊缝，需要全程保持谨慎。这些特点最好在焊接工艺上注明。

(3)图14对比发现，增加副焊缝成为双面焊后，主焊缝应力分布受到的影响不大，两种情况下曲线几乎融合，再次与体积云图吻合。这个结果非常好，主焊缝完全焊透或施加双面焊均可消除母材间的缝隙，都可以避免缝隙腐蚀，而后者主副焊缝总截面比单面焊缝截面增大，成型好，提高了观察窗承重和工作时遭遇意外冲击的能力。

另外，通过90 ℃和290 ℃两种条件下模拟结果(90 ℃云图和曲线不再示出)对比发现后者上述规律完全适用于前者，只是整体或焊接路径上最大热应力统一比90 ℃大很多。热变形产生的热应变等于α(φ-φ0), 其中α是材料的线膨胀系数，φ是弹性体内任一点现时温度，φ0是初始温度。显然温度越高，热应变越大，由炉盖内外壁产生的约束越严重，从而使热应力成数倍增加。这要求改进设计，严格控制冷却水进出口截面积和水压，保证一定流量和流速,使窗体能够充分冷却。设置冷却水温检测及超温报警，当冷却水温超过50 ℃时，使相应报警指示灯发亮并发出有声报警，便于及时处理故障，以免耽误时机，造成观察窗温度过高，热应力增加，使焊缝更容易产生裂纹。

单晶炉每个生产周期，窗口都要经历升温和降温的过程，难免遭遇冷裂纹的生成温度区间，所以窗形和双面焊的规律于此也有一定影响。

实践证明：采用DRE观察窗、单面焊、冷却水温控制失灵等因素会导致严重安全事故，即使在样机冷炉试验时能正常工作，出厂使用时寿命短频繁漏水，而采用C&R、DCU和DCI观察窗、双面焊以及控制冷却水温不超过规定值能有效避免泄漏事故，极大增加设备使用寿命。上述热应力模拟结果与其指导下工程实践成果是一致吻合的。同时说明以冯米斯应力作为裂纹和漏水的关联参数是合适的。与此相似，文献[9]提到晶体中的位错密度依赖于冯米斯应力，而位错观点认为裂纹形核由位错产生。甚至，通过一定的微分方程可以将热应力和位错联系起来。几个研究小组根据这种方程，由数值模拟所得热应力来预测位错密度。文献[10]比较了他们之间的模拟结果以及模拟结果与特性实验测量的结果，发现具有相同的变化模式。这对不锈钢合金材料承受的热应力在位错产生中所扮演的角色具有一定的参考意义。

4 结 论

导致焊接接头产生裂纹，甚至脆性断裂的内应力由多种因素决定，经验提示，炉盖的窗口形状对其工作热应力有重要影响，应把它作为阻止该部位产生裂纹，出现漏水的考虑因素之一。炉盖两种封头和六种形状观察窗可组合成12种结构，在单面焊和双面焊两种情况下，先对炉盖整体模拟计算，再用子模型技术对窗口局部重新计算提高精度，按几何边界提取主焊缝整体及各个区域数据，列成表格，主焊缝三条棱边路径的数据绘成应力分布线，研究发现：

(1)在单晶炉工作时，内外壁横截面均为正方形或矩形的两种窗形焊缝的热应力极值最大，设计炉盖时应选用圆形窗或者内壁带圆弧的长条窗。

(2)增加副焊缝成为双面焊后，主焊缝的应力分布几乎没有变化，新增加的约束对其影响甚微。从而整体上提高了观察窗承重和遭遇意外冲击的能力。

(3)温度越高，应力越大，应采取措施，避免窗体冷却水温超过规定值。

(4)对不同观察窗口形状的研究，可推广应用到取光口和类似观察窗的真空接口。