纤维缠绕复合材料压力容器多型封头对比分析

蔡 强，赵晓宁，李新田，淡林鹏，蒲晓航，黄慧慧

(中国运载火箭技术研究院，北京 100076)

0 引言

纤维缠绕复合材料压力容器(以下简称复材容器)由于具有轻质高强的优点，在航天技术领域得到了广泛的应用[1-7]。复材容器一般由前后封头和筒段组成，三者一体缠绕成型，在前后封头缠绕过程中，缠绕角、纤维厚度和纤维应力等参数是不断变化的，不同的缠绕线型和子午线形状直接影响复材容器的承压能力，因此封头设计及分析工作是复材容器设计的核心内容。

复材容器封头的设计分析多采用网格理论计算，内压完全由纤维承担，树脂基体仅起到黏合作用，纤维缠绕通常采用测地线缠绕理论，不用考虑摩擦力的因素，纤维能够在芯模上稳定铺敷不打滑[8-10]。近年来，有关学者引入经典层板理论和非测地线纤维缠绕轨迹，考虑了树脂基体的承力并扩大了纤维缠绕轨迹设计空间[11-19]。

在方案论证阶段，通常需要快速开展封头方案的迭代设计、优化分析，因此亟需建立不同封头的快速方案评估模型，并通过对比分析优选出满足设计要求的方案。为此，本文系统整理出螺旋缠绕封头、螺旋缠绕椭球封头、平面缠绕封头和平面缠绕椭球封头4种封头的控制方程，设计上采用成熟可靠的网格理论和测地线理论，通过实例计算对比分析缠绕线型和封头子午线类型对复材容器性能的影响。

1 复材容器参数模型

1.1 几何参数模型

本文主要研究对象是复材容器封头，但是筒段的长度、外径和壁厚直接影响封头的参数，因此采用图1所示的封头和筒段一体化的几何参数模型。封头的主要参数有子午线形状、缠绕角、封头壁厚和纤维应力。

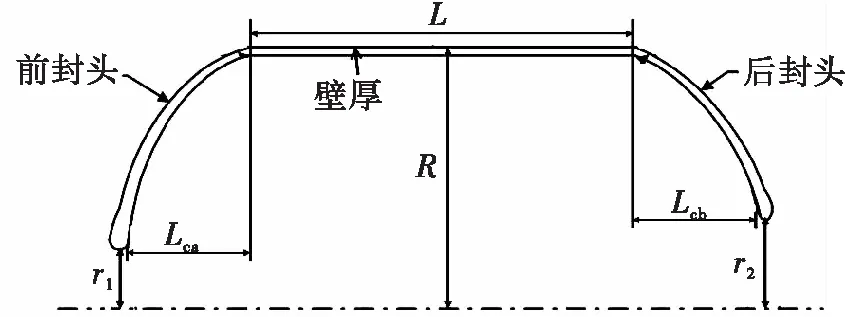
图1 复材容器参数模型Fig.1 Simplified parametric model of filament-wound composite pressure vessels

复材容器成型工艺是在芯模上按照一定的轨迹连续缠绕浸胶的复材纤维带，常用的纤维缠绕线型轨迹有螺旋缠绕和平面缠绕2种方式。

螺旋缠绕线型如图2所示，其中r1为给定的筒段径向位置；α1为筒段纤维缠绕角；r2为给定的封头径向位置；α2为封头纤维缠绕角。纤维轨迹严格满足稳定的测地线，即r1sinα1=r2sinα2，不存在滑纱的风险，同时封头各点纤维应力相等，但是要求前后极孔直径相等。

图2 螺旋缠绕线型Fig.2 Helical filament winding

平面缠绕线型如图3所示，其中φFront pole为前极孔直径，φBack pole为后极孔直径，前后极孔直径可以不等，α为纤维缠绕角。平面缠绕线型轨迹是从一个极孔直接缠绕至另一个极孔，这种线型只能用于长度较小的壳体，要求壳体长径比L/D≤2。

图3 平面缠绕线型Fig.3 Polar filament winding

以上2种线型，封头和筒段一体缠绕，纤维应力连续变化，承内压能力较好，但是封头子午线形状受限于缠绕线型无法自主设计，工程上为了设计和工艺方便，并提高体积装填率，经常采用椭球封头，即封头子午线方程满足椭圆弧曲线方程

r2/R2+z2/B2=1

(1)

令椭球比

m=R/B

将不同缠绕线型和封头子午线形状组合，常用的封头形式可以分为螺旋缠绕封头、螺旋缠绕椭球封头、平面缠绕封头和平面缠绕椭球封头4类。

1.2 网格理论假设

封头设计及分析时采用如下的网格理论，有如下假设条件：

1)复材容器的载荷全部由纤维的拉伸强度承担，树脂基体仅对纤维起黏结、定位的作用，使纤维强度充分发挥；

2)在整个复材容器上纤维连续缠绕，分布均匀且对称；

3)复材容器为薄壁结构件，应力沿壁厚均匀分布，无弯曲应力，内部压力处处相等，均匀一致；

4)复材容器前后封头和筒段螺旋向一体成型，然后筒段补充环向缠绕，即前后封头为“螺旋向”或“平面”缠绕线型，筒段为“螺旋向+环向”或“平面+环向”缠绕线型。

1.3 筒段壁厚计算方法

筒段长度L和外径R一般根据约束条件给定，筒段壁厚hfc与封头形式无关，本文采用参考文献[20]中方法计算，为了方便下文引用，列出筒段壁厚

(2)

式中：pb为容器最大内压；hfα为纤维螺旋向或平面缠绕壁厚；hfθ为环向壁厚；σfb为纤维的实际发挥强度。

2 复合容器封头设计模型

2.1 设计规则及控制方程

一般封头的几何构型如图4所示，封头上采用螺旋缠绕或平面缠绕线型，纤维分布满足以下3个规则：

规则1：纤维排列关于子午线对称；

规则2：纤维与子午线的夹角即缠绕角α是关于平行圆半径r的函数，α=α(r)，赤道圆上的缠绕角等于圆筒上的纵向缠绕角α0，在极孔上，α=π/2；

规则3：根据物质守恒定律，通过平行圆法截面上的纤维总量等于通过赤道圆法截面上的纤维总量，且等于通过圆筒横截面上的纤维总量。因平行圆半径是变化的，因而封头厚度hf也是r的函数，即hf=hf(r)，在赤道圆处，封头壁厚等于筒段壁厚hfα，即hf=hfα。

图4 一般封头几何构型Fig.4 Geometry of general dome

极坐标条件下，一般回转体封头的曲面方程

S(θ,z)={rcosθ,rsinθ,z}

(3)

式中：r=r(z)为封头的母线方程，r是平行圆半径坐标；z为回转体轴线坐标；r和z均大于0，θ为沿纬度圆的包角。

引入无量纲参数

(4)

根据规则1～规则3，可以推导出一般封头的无量纲化控制方程[20]

(5)

2.2 螺旋缠绕封头

(6)

图5 螺旋缠绕封头子午线拐点及处理方法Fig.5 Inflection point and modified meridian of helical winding dome

2.3 螺旋缠绕椭球封头

椭球封头的子午线方程是给定的椭圆弧，将式(4)代入式(1)得出无量纲化的子午线方程

ρ2+m2ε2=1

(7)

对ρ求一阶和二阶导数，可得

(8)

(9)

值得注意的是该封头不再满足等应力条件。

2.4 平面缠绕封头

从图3中可知，平面缠绕筒段纤维缠绕角α0满足

(10)

根据图6中的平面缠绕封头的几何关系，得出

ρsinθ=ρe+εtanα0

(11)

(12)

式中ρe为赤道处纤维轨迹起点坐标在子午线平面的投影。

图6 平面缠绕封头几何关系Fig.6 Geometry of polar winding dome

联合式(5)、式(11)和式(12)，得出平面缠绕封头的控制方程

(13)

与椭球封头相似，平面封头曲率在缠绕角α=54.7°时也会出现拐点，采用相同的处理方法，在等曲率点α=45°以后用圆弧替代原子午线。

2.5 平面缠绕椭球封头

将式(8)中椭圆弧二阶导数代入式(13)，得出平面缠绕椭球封头的控制方程

(14)

3 实例及结果分析

3.1 模型验证

为了验证本文计算模型的正确性，选取极孔半径ρ0=0.1、0.2、0.3、0.4共4种工况，分别对比螺旋缠绕封头曲线与参考文献[21]中的等应力封头曲线，计算结果如图7所示，可见吻合性非常好。

3.2 实例对比分析

以下针对4种不同类型复材容器封头的实例进行讨论，采用T700/树脂基体复合材料，纤维体积含量为60%，复合密度为1.56g/cm3，最大设计压强为10 MPa，筒段外径均为φ1 000 mm。4个实例三维模型如图8所示，其他几何参数如表1所示。

图7 封头设计模型验证Fig.7 Verification of dome design model

图8 设计实例三维模型Fig.8 3D solid geometric models of cases

表1 实例几何尺寸

由表1可以看出，4个后封头尺寸相同，以下对比4个后封头的设计结果。封头的子午线、缠绕角和壁厚的设计结果对比如图9所示。

1)子午线设计结果：除螺旋缠绕封头高度较大外，其余3种封头子午线轮廓设计结果相近，螺旋缠绕封头高度(332 mm)比其余封头高度大了约8.9%。另外，平面缠绕封头和螺旋缠绕封头在等曲率点前后变化趋势连续无奇异点，证明2.2节处理方法的正确性。

2)缠绕角设计结果：相同缠绕线型的缠绕角度变化趋势相似，且变化连续，z=250 mm之前螺旋缠绕线型缠绕角(初始缠绕角约15°)大于平面缠绕线型(初始缠绕角约30°)，之后变化趋势一致，由于螺旋缠绕封头高度较大，因此在极孔附近缠绕角变化较缓。

3)封头厚度设计结果：封头厚度的变化趋势同缠绕角，相同线型相似，且螺旋缠绕线型平均封头厚度大于平面缠绕线型。

图9 后封头设计结果对比Fig.9 Comparison of dome design results

4种封头的纤维应力对比如图10所示，可见：

图10 后封头纤维应力设计结果对比Fig.10 Comparison of fiber stress design results for rear dome

工程上为了解决极孔附近应力较大问题，通常在此处进行局部补强，另外在极孔处通过缠绕固定铝合金或钛合金接头的设计来弥补应力突变带来的结构强度不足。

为比较4种后封头的综合性能，引入参考文献[8]中的综合性能系数pV/W(p为容器内压；V为封头体积；W为封头质量)。详细对比如表2所示。

1)由于封头高度的原因，螺旋缠绕封头自由容积最大，其余三者相近。

2)由于螺旋缠绕封头平均厚度大于平面缠绕，相同缠绕线型的封头质量相近，螺旋缠绕线型封头的质量大于平面缠绕线型。

3)相同缠绕线型的综合性能系数pV/W相近，平面缠绕线型的封头的pV/W值优于螺旋缠绕线型。

表 2 后封头性能参数对比Tab.2 Comparison of performance parameters for rear dome

综上，相同缠绕线型的缠绕角、壁厚和性能参数接近，平面缠绕线型封头质量轻、pV/W值高，螺旋缠绕线型纤维受力较好。为了避免封头曲面曲率的不连续性，同时考虑设计和加工的便捷性，推荐采用螺旋缠绕椭球封头或平面缠绕椭球封头。

4 结论

本文基于复材容器的参数模型，系统研究了壳体筒段和封头的设计方法，完成了螺旋缠绕封头、螺旋缠绕椭球封头、平面缠绕封头和平面缠绕椭球封头等4类封头控制方程的建模，通过对4种后封头实例的子午线、缠绕角、壁厚、纤维应力以及综合性能参数对比，发现相同缠绕线型的封头设计结果相似，建议根据实际应用情况采用螺旋缠绕椭球封头或平面缠绕椭球封头，以避免子午线曲率的拐点，同时有利于加工制造。