基于自适应滑模观测器的终端角度约束制导律

赵 斌，朱传祥，仝 云，胡 阳，李 权，蒋瑞民

(1. 西北工业大学航天学院，陕西 西安 710072； 2. 西北工业大学机电学院，陕西 西安 710072；3. 上海机电工程研究所，上海 201109)

0 引 言

精确打击是现代战争的主要作战形式，是加速战争进程，决定战争胜负的关键要素。导弹的制导系统是导弹的大脑和中枢神经，它直接决定着制导性能和制导精度[1]。早期的制导方法大都基于比例导引及其各类改进方法实现[2-3]，此类方法在目标匀速直线运动且忽略速度衰减的条件下被证明是最优制导方法[4]。

然而，随着技术的发展，来袭目标速度越来越高，同时具有机动能力，这要求导弹不仅要准确命中目标，而且要以特定的攻击角度命中目标以充分发挥战斗部的毁伤效能。因此，研究具有终端攻击角度约束的制导律成为新的挑战。

最早的角度约束制导律从比例导引法发展而来[5-8]，这些方法针对静止目标和非机动目标具有较好的拦截效果，而在拦截大机动目标时，由于缺少目标运动信息，拦截精度难以保证。

为了有效应对目标未知机动引起的系统不确定问题，变结构控制被用于进行制导律设计[9-12]。此类方法只需要保证滑模变量符号项的系数大于不确定上界，就可以实现对于参数摄动和外部扰动的鲁棒性。由于目标机动是未知的，因此该参数的选择具有一定困难。如果选择过大，会导致系统制导指令抖动较大；如果选择太小，则又难以保证闭环系统稳定性。

针对以上问题，本文提出一种基于非奇异终端滑模[13-14]的终端角度约束制导律。针对目标机动引起的不确定性设计了一种新型自适应二阶滑模观测器，以实现对系统不确定性的有限时间估计，在此基础上证明了闭环系统的有限时间收敛特性。

1 数学建模

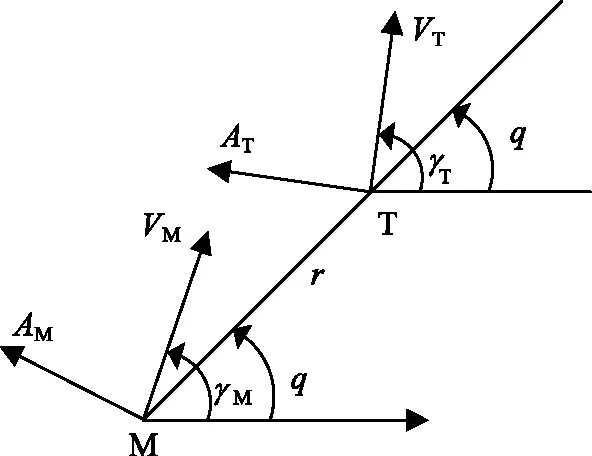
图1 二维弹-目相对关系Fig.1 Two-dimensional engagement geometry

考虑二维场景下的弹-目相对运动关系如图1所示。M,T分别代表导弹和目标；VM,AM代表导弹的速度和加速度；VT,AT代表目标的速度和加速度；r,q分别是弹-目相对距离和惯性系视线角；γM,γT分别为导弹与目标的航迹角。

由此，可建立非线性弹-目相对运动方程[1]，即

(1)

不失一般性，本文制导律设计时引入如下假设：

1) 假设1： 忽略导弹自动驾驶仪和导引头的动态特性，即认为弹体可以理想实现制导过程；

2) 假设2： 在短暂的末制导过程中，假设导弹与目标速度大小不变。

定义末制导的终端角θ(te)为命中瞬间导弹速度与目标速度方向的夹角。该角度与终端弹目视线角q(te)存在一一对应关系[15]，即

(2)

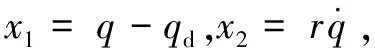
(3)

其中：不确定性Δ=ATcos(q-γT)/r表征由目标加速度引起的干扰项；u=AMcos(q-γM)为待设计制导指令。

本文的目标是设计制导律u，使得在未知干扰Δ存在的情况下，状态方程(3)所示系统的状态有限时间收敛至零。

2 引理及定义

定义1：非奇异终端滑模态[16]和快速非奇异终端滑模[17]分别定义为

(4)

(5)

其中：x∈R；sigβ(x)=|x|βsign(x)；s为滑模变量。

根据定义，可知其一阶微分可表述为

(6)

(7)

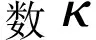
1) 有限时间稳定[16]：

(8)

其中：t>t0，t0是系统运行的初始时刻。若式(8)成立，则该函数将在有限时间收敛至零，且收敛时间T1满足

(9)

2) 快速有限时间稳定[17]：

(10)

若式(10)成立，则该函数有限时间收敛至零，且收敛时间T2满足

(11)

3 自适应滑模观测器设计与稳定性分析

给定非线性状态方程

(12)

其中：d为系统不确定；dU为未知的不确定微分上界。设计其自适应参数及自适应律选择为

(13)

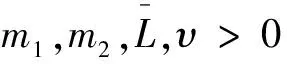
选择Lyapunov函数为

Vζ=L-2ζTP(t)ζ

(14)

(15)

根据矩阵及向量相关知识可知

(16)

同时对向量ζ进行求导可得

(17)

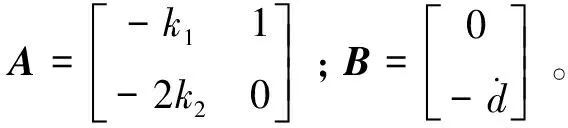
定理1： 对于式(12)所示系统选择式(13)所示的自适应律及式(14)所示的Lyapunov函数，并且相关矩阵参数满足

(18)

其中，Q(t)=-ATP(t)-P(t)A=

则系统状态ξ1(t),ξ2(t)有限时间内收敛于零。

证明：对式(14)所示的Lyapunov函数求导可得

(19)

将式(13)、式(17)代入式(19)可得

(20)

根据式(18)可知

(21)

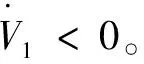
(22)

最终，综合式(18)～(22)可知

(23)

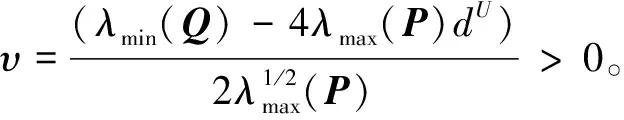
因此，根据引理1可知，系统状态ξ1(t),ξ2(t)有限时间内收敛于零。

基于定理1可以设计如下的干扰观测器，对状态方程(3)所示系统中目标机动引起的不确定性进行精确估计，即

(24)

根据定理1可知，干扰估计偏差在有限时间内将收敛至有界范围中，即满足

(25)

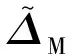
4 终端角度约束制导律设计与分析

定理2: 针对状态方程(3)所示系统设计非奇异快速终端滑模(如式(5)所示)，设计式(24)所示的干扰观测器，同时设计制导律为

(26)

式中：h1,h2>0；0<μ<1。由此可得：

1) 滑模变量有限时间收敛于|s|≤Δ1；

2) 状态有限时间收敛于|x1|≤Δ2,|x2|≤Δ3。

其中，各个收敛域为

(27)

证明：该定理证明过程可以分为两步完成。

1) 证明滑模变量的有限时间收敛

对滑模变量求导，并代入式(3)和式(26)可得

(28)

由于α2>0,1<β2<2，可知α2β2|x2|β2-1>0。

根据式(25)和代数不等式可知

(29)

选择Lyapunov函数为

(30)

对式(30)求导，并代入式(28)～(29)可得

(31)

其中：

(32)

① 当x2≠0时，若选择参数满足

(33)

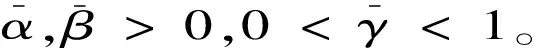
② 当x2=0且s≠0时，将式(26)代入状态方程(3)中的第2式，可得

(33)

由于s≠0，因此系统状态x2不会一直停留在x2=0,s≠0，则x2=0不是系统的吸引子。

2) 给出相关变量的收敛域

式(33)给出了滑模变量有限时间收敛的条件，由此可知滑模变量的收敛域可表述为

(34)

此外式(5)所示滑模面可等价写为

(35)

(36)

因此，对比式(35)、式(36)和式(5)，可知

(37)

(38)

证明完毕。

5 数学仿真与分析

本章通过数学仿真对上述算法进行验证。算法的制导律参数见表1，干扰观测器参数见表2，初始仿真场景见表3。仿真周期选择为1 ms，过载限幅为20g。仿真结果如图2～3所示。

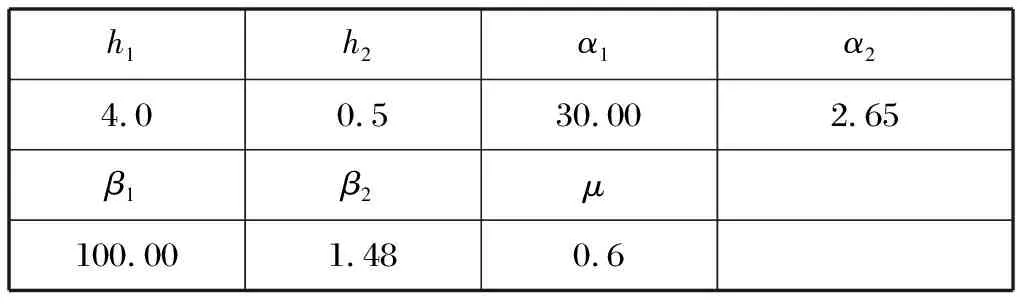
表 1 制导律参数

表2 干扰观测器参数Tab.2 Parameters of the disturbance observer

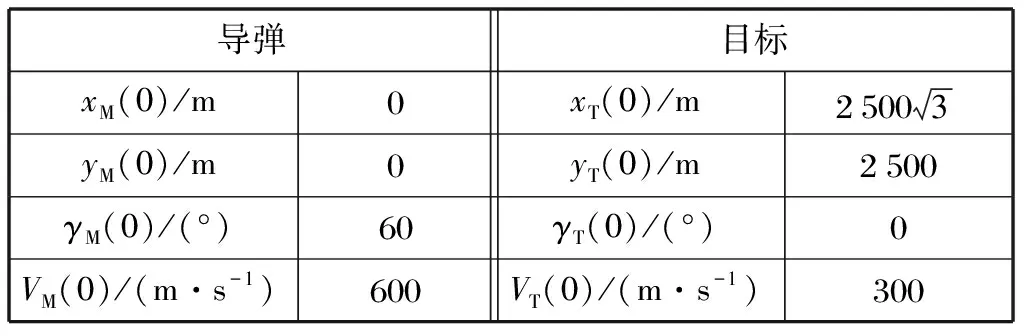
表3 导弹与目标初始条件Tab.3 Initial conditions for missile and target

图2 场景1下的仿真结果Fig.2 Simulation results in scenario 1

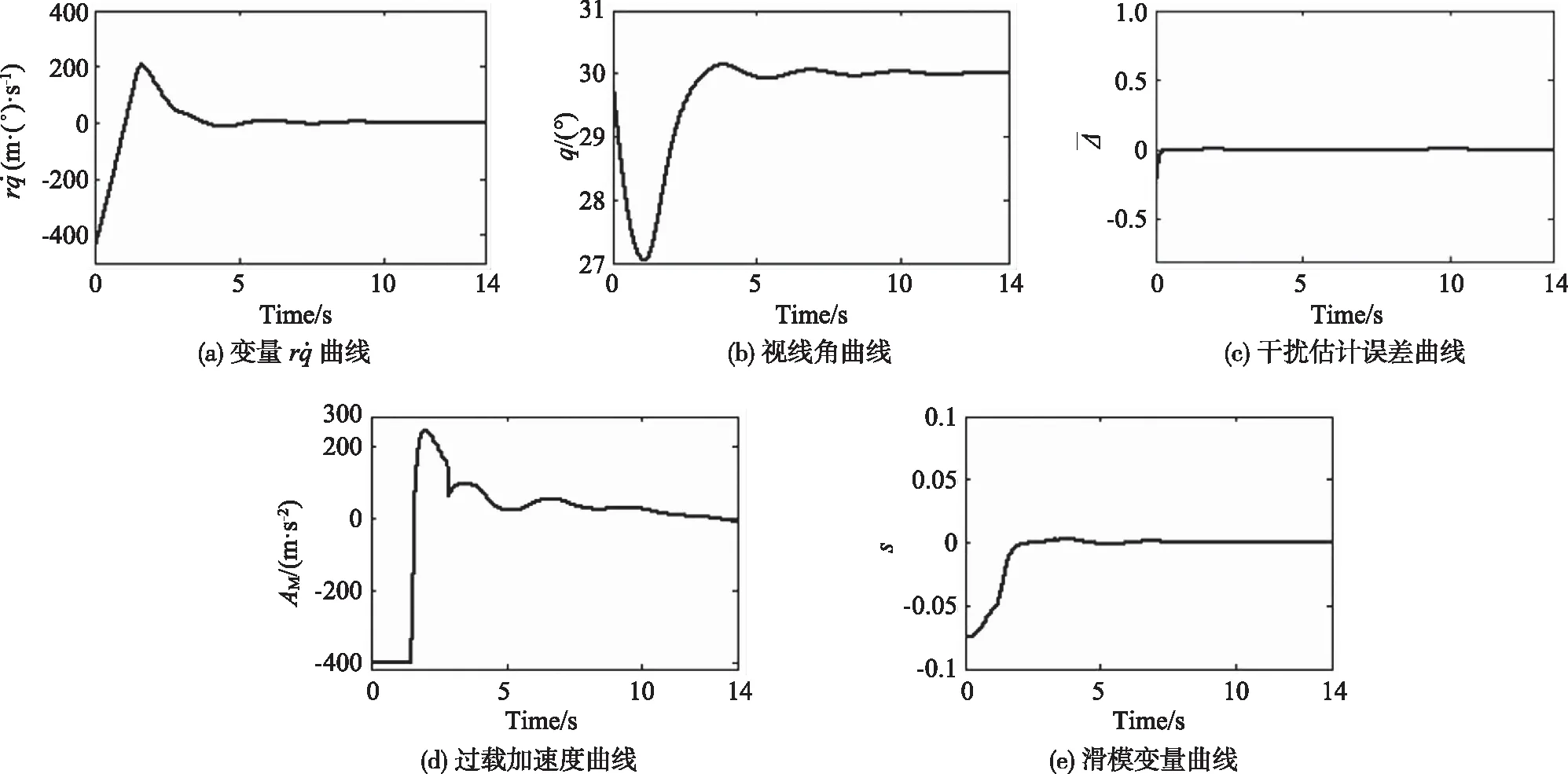
图3 场景2下的仿真结果Fig.3 Simulation results in scenario 2

仿真场景1：AM=5gcos(πt/4)，目标正弦机动，设置终端约束角度为20°；

仿真场景2：AT=5g，目标常值机动，设置终端角度为30°。

为了便于分析系统命中精度，定义新的变量

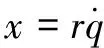
(39)

具体分析如下：

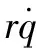
2) 从图2(b)和图3(b)可以看出，两种场景下最终视线角分别收敛于20°和30°，这与仿真预设的终端约束角度一致，说明了算法对于终端角度约束的有效性；

3) 从图2(c)和图3(c)可以看出，所设计的干扰观测器工作良好，可以实现有限时间内对目标机动引起的不确定性的精确估计，这符合定理1的相关结论；

4) 从图2(d)和图3(d)可以看出，整个制导过程中导弹加速度指令光滑有界，适合弹体自动驾驶仪的跟踪；

5) 从图2(e)和图3(e)可以看出，所设计的非奇异快速终端滑模变量均有限时间收敛至零，这符合定理2的相关结论。

5 结束语

本文提出了一种考虑终端角度约束的机动目标拦截制导律。针对目标未知机动引起的系统不确定性，采用本文提出的自适应滑模干扰观测器，实现了估计误差的有限时间收敛，该方法也可推广用于其他干扰微分有界的不确定系统。基于快速非奇异终端滑模，结合有限时间收敛理论，可以确保系统状态在滑模趋近阶段以及滑模面上运动的有限时间有界收敛特性。