卫星姿态控制的变结构滑模控制方法

李由,史梦芯

(西安电子科技大学空间科学与技术学院,710126,西安)

卫星的姿态控制对于航天技术的发展和应用起着关键作用,并且随着航天技术的日益发展和广泛应用,卫星的姿态控制问题越来越受到人们的关注。目前,已有许多研究人员对于卫星姿态控制的基本理论和问题进行了探究[1-4],这些成果对于实际工程起着重要作用。滑模控制作为研究卫星的姿态控制的众多研究方法之一,虽然在滑模面上的系统状态具有鲁棒性强、稳态精度高等优点,但是滑模控制在收敛速率方面存在不足,并不能满足对快速机动卫星的收敛速率要求。这就要求设计新的滑模控制方法满足卫星控制系统快速收敛的要求。

对于经典滑模控制方法,针对系统状态的有限时间收敛和良好稳定性的问题,冯昱澍等[5]在考虑扰动存在的情况下,为提高闭环系统的鲁棒性等特性,设计出自适应积分滑模控制器,而宋杉等[6]设计出自适应固定时间滑模控制器。王小婷[7]针对挠性卫星姿态系统外部干扰上界未知的问题,结合干扰自适应律和滑模控制设计了干扰自适应滑模控制器。上述研究和所涉及的控制方法都利用了滑模控制,但是针对滑模控制的收敛速率较低这一缺点并没有进行研究和解决。

对于变结构滑模控制方法,梁健等[8]针对敏捷卫星大角度姿态机动的问题,考虑变结构控制的系统参数变化和干扰具有很强的鲁棒性等特点,设计了基于变结构滑模控制器的敏捷卫星姿态机动方法。董超等[9]针对柔性航天器挠性附件振动与姿态机动耦合降低控制精度的问题,考虑控制力矩抖振和系统参数鲁棒性差等缺点,设计了改进的变结构滑模控制器。变结构滑模控制可以很好地改善经典滑模控制在收敛速率方面较低的问题,但是上述研究并没有将变结构滑模控制与其他控制方法进行比较,得出变结构滑模控制的优越特性。

对于滑模控制方法在实际工程中的应用,王家琪等[10]为保证控制系统的控制效果,针对抑制控制系统中的不确定性和外干扰等问题,考虑提高收敛速度的要求,设计了一种基于干扰观测器的新型滑模控制律。唐寅峰等[11]针对清理太空垃圾和利用太阳能的问题,并考虑消除弹射系统对空间太阳能电站的姿态影响,结合双环滑模变结构控制方法设计了空间太阳能电站。众多研究者在研究卫星控制系统时都利用了变结构滑模控制方法[12-16]。在上述的工程应用中,作者只是应用滑模控制来研究系统的稳定性和鲁棒性,并没有将收敛速率作为研究问题进行研究。此外在实际工程中,尤其在航天领域有许多特定系统都有力矩上界和角速率范围[17],这些重要因素也必须要着重考虑和研究。

对于经典滑模控制和变结构滑模控制,不仅在航天科技方面得到应用,而且在机器人[18]、机械臂[19]、同步电机[20-21]、无人机[22]、Vienna整流器[23]、导弹制导[24]、温度控制[25]等方面都有广泛应用。这足以证明经典滑模控制和变结构滑模控制在众多科技领域都有利用价值,因此发展和研究滑模控制对科技发展有着重要的推进作用。

针对卫星姿态机动控制问题中经典滑模控制存在收敛速率较低的缺陷,设计了一种变结构滑模控制方法。其主要的优势在于其维持了经典滑模控制器结构简单、鲁棒性强的优势,还大幅度提升控制系统的收敛速率。此外本文还讨论系统参数与控制力矩幅值、角速度幅值之间的约束关系,保证了控制器全程不超其上界。利用Lyapunov稳定性理论证明控制器的全局稳定性,最后通过数值仿真验证本文所提出的变结构滑模控制器的有效性和优越性。

1 数学模型

刚体卫星的姿态动力学模型可以写为

(1)

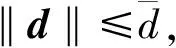
(2)

同时注意到在实际工程应用中转动惯量矩阵J一般无法做到精确已知,因此令

(3)

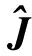
基于四元数描述的卫星姿态运动学模型的表达式为

(4)

式中:q0为姿态四元数标部;qv为姿态四元数矢部。矩阵F的奇异值满足如下性质

λM(F)=1

(5)

若无特别说明,在本文中,以λ(A)、λm(A)、λM(A)分别表示矩阵A的奇异值、最小奇异值与最大奇异值。

2 变结构滑模控制器

一般在卫星姿态控制领域,经典的滑模控制中滑模面结构可以写为

s=ω+kqv,k>0

(6)

当系统状态位于该滑模面上时有

ω=-kqv

(7)

以及

(8)

根据式(6)和式(7)可以看出,系统在该滑模面上具有指数收敛的特性。值得注意的是该滑模面的重要特性之一是角速度与四元数矢部的反向,同时欧拉角的运动学方程表示为[1]

(9)

式中:α为姿态角速度与欧拉轴亦即姿态四元数矢部的夹角。

从式(9)可以得出,在角速度范数一定的条件下,角速度与四元数矢部反向时欧拉角具有最快的收敛速率,这也就意味着在该条件下系统对于角速度的利用效率最高,正是因为如此经典滑模控制方法在提出之后得到了众多学者的关注。

经典滑模控制器的一大弊端在于其较慢的收敛速率,经典滑模面锁定滑模参数k的做法使得卫星的姿态角速度范数始终正比于姿态四元数范数,而随着系统状态的收敛,角速度的范数也随之急剧下降,从而导致了系统收敛速率的下降。为了解决这一问题,即提升系统收敛速率,增大滑模参数k是一种较为直观、可行的手段,但是其带来的弊端则是系统在控制初期所需要的控制力、控制力矩较大,这就会导致出现控制输出饱和的问题,进而导致系统无法追踪期望轨迹。同时该方法还有可能使得系统角速度范数超过其上界,从而带来飞轮过载、推力消耗加剧、挠性形变增大、姿态确定精度下降等不利影响。

针对上述弊端本文提出一种新的滑模面结构如下

s=ω+kqv,k(0)>0

(10)

式中:滑模参数k的初值k(0)为正常数;p为待设计正常数;ε为一小的正常数。

变结构滑模面(10)分为两个阶段,第1阶段亦即‖s‖≥ε时,系统状态尚未到达滑模面,此时角速度矢量与姿态四元数矢部尚未反向,滑模面(10)为经典滑模面,同时滑模参数不进行更新;而在第2阶段亦即‖s‖<ε时,系统到达或近似到达滑模面,角速度矢量与四元数反向,此时滑模参数k开始更新,同时基于其更新律可以看到其导数始终为正,这就意味着在系统状态到达滑模面之后,以较小的滑模参数初值开始运行,同时随着系统状态的收敛滑模参数开始实时增大,进而角速度的范数也能够随之得以提升,从而实现提升系统收敛速率的目的,此外值得注意的是在该滑模面上系统姿态角速度始终与四元数矢部保持反向,这也使得经典滑模面的优点得以保持。

基于滑模面(10)的滑模控制器可以写为

u=

(11)

其中

(12)

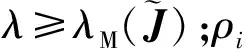
ρi=

(13)

其中

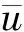
接下来对控制器(11)进行稳定性证明。选取Lyapunov函数如下

(14)

在系统尚未到达滑模面之前,即‖s‖≥ε时,对Vs求导并代入控制器(11)可以得到

-ρ1kssTs≤0

(15)

在系统到达滑模面之后,即‖s‖<ε时,对其求导并代入控制器(11)可以得到

(16)

从而有滑模状态s一致渐近稳定,而由前文讨论,系统状态ω与qv在滑模面s=0上一致渐近稳定,从而系统(1)、(4)在控制器(11)的作用下一致渐近稳定,系统稳定性证明完毕。

3 系统约束讨论

首先讨论系统控制力矩对于控制参数的选取约束。考虑到控制器(11)中滑模参数的比例项-kss可以通过控制增益因子ρi进行放缩,因而控制器(11)中的第一项并不影响控制力矩饱和问题,关键是保证控制器中之后几项不超过系统上界。在系统尚未到达滑模面时,有

(17)

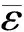
(18)

即可保证系统状态在滑模面之外时,所需要的控制力矩不超过上界的要求。

当系统状态到达滑模面之后,姿态角速度满足

ω=-kqv

(19)

同时注意到

(20)

从而可以得到

(21)

定义辅助变量z如下

(22)

(23)

从而当z取极值时有

(24)

进而有

(25)

因此只需满足下式

(26)

即可保证系统控制力矩全程不超过其上界。

综上所述,系统控制力矩对于滑模参数的约束可以写为

(27)

式(27)中的第1式是系统对于滑模参数初值的约束,第2式是对于滑模更新参数的约束,二者共同保障系统的控制力矩约束。

(28)

即可使该阶段系统角速度范数不超过其上界。

在系统状态到达滑模面之后,计算角速度范数的导数可以得到

(29)

从而当角速度范数取得其极值时有

(30)

从而可以得到

(31)

因此系统角速度范数对于控制参数的约束为

(32)

式(32)中的第1式为角速度对于滑模参数初值的约束,而第2式则为角速度对于滑模更新参数的约束。

4 收敛性对比分析

对于卫星姿态控制而言较为常用的经典滑模面表达式为

s=ω+kqv

(33)

式中:k为正常数。

当系统状态到达滑模面时,有ω=-kqv,因此选取Lyapunov函数如下

V=1-q0

(34)

对其求导可以得到

(35)

对于本文设计的变结构滑模控制器,当系统到达滑模面时,有ω=-kqv,因此同样选取Lyapunov函数式(34)。对其求导可以得到

(36)

5 数值仿真

首先设定系统参数如下

(37)

同时为了说明本次研究所提出算法的有效性与优越性,将以如下的经典滑模控制器(38)作为对比,仿真结果如图1～图4所示。

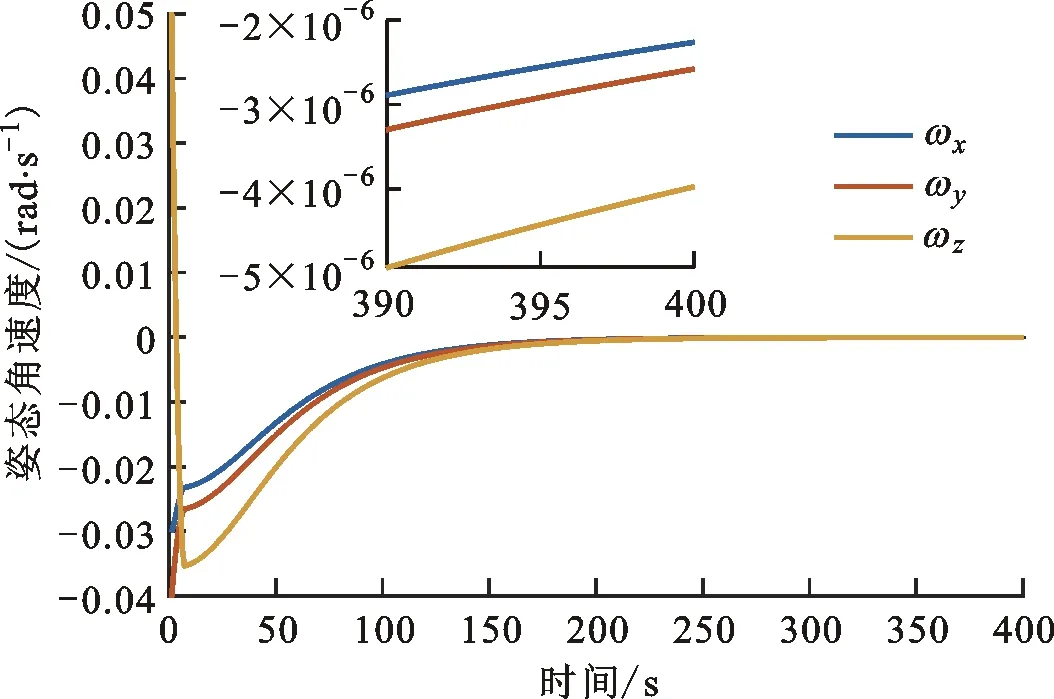
图1 经典滑模控制器的姿态角速度曲线

图2 经典滑模控制器的姿态四元数曲线

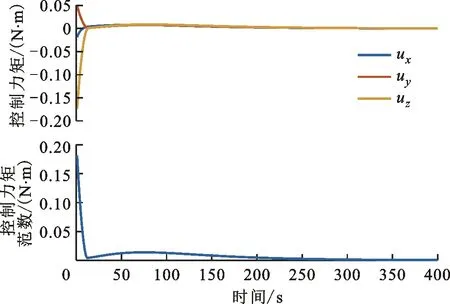
图3 经典滑模控制器的控制力矩及其范数曲线

图4 经典滑模控制器的角速度范数曲线

(38)

如果使经典滑模的参数与变结构滑模的参数相同,由图1～图4可以看出,系统能够稳定收敛,收敛时间约为240 s,此外在400 s时的角速度与四元数稳态精度分别为5×10-6rad/s与8×10-5。通过仿真结果可以发现,此条件下的控制力矩范数和角速率都没有超过各自的上界,但是此条件下的收敛速率远低于k较大时和变结构滑模控制的收敛速率,这表明同等条件下经典滑模控制的收敛速率远低于变结构滑模控制,不能够满足控制系统的收敛速率要求。

为增加经典滑模控制与变结构滑模控制的对比效果,将经典滑模控制器(38)中的k提高数倍使得其与变结构滑模控制的收敛速率在同一级别,参数修改如下式所示,仿真结果如图5～图8所示。

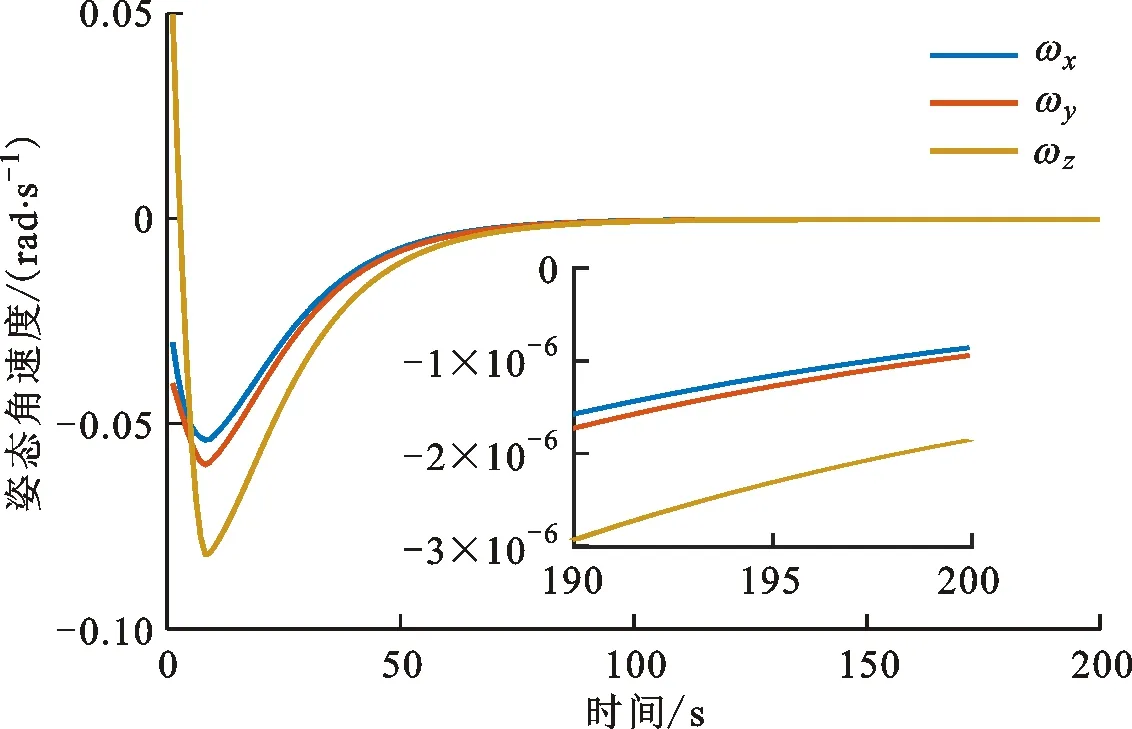
图5 经典滑模控制器的姿态角速度曲线

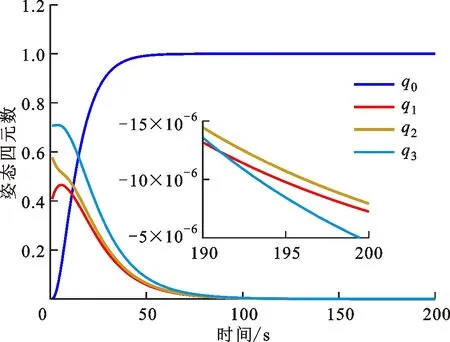
图6 经典滑模控制器的姿态四元数曲线

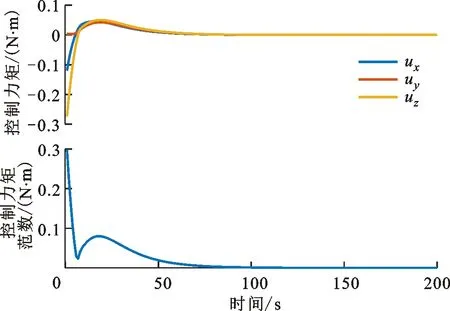
图7 经典滑模控制器的控制力矩及其范数曲线

图8 经典滑模控制器的角速度范数曲线

k=0.12,ks=2

(39)

如果使经典滑模的收敛速率与变结构滑模的收敛速率达到同一级别,则需要使得经典滑模参数k是变结构滑模参数k的数倍。基于图5～图8可以看出,系统能够稳定收敛,收敛时间约为100 s,此外在200 s时的角速度与四元数稳态精度分别为3×10-6rad/s与1.5×10-5。通过仿真结果可以看出,此条件下的仿真结果使得系统初始控制力矩较大,由图7和图8可以很明显地看出,虽然整个控制力矩不超过系统上界,但是存在约10 s的区间(5～15 s)超过系统的姿态角速度上界。若采用飞轮、力矩陀螺等角动量交换装置作为控制执行机构,角速度超过上界意味着需要通过推力器工作对角动量机构进行卸载,进而影响到系统的寿命,这一弊端在实际工程应用中对卫星的寿命限制较为严重。

接下来给出本文所提出的变结构滑模控制器的仿真结果。首先选取控制参数如下

k(0)=0.05,p=0.08,λ=3,ks=2

(40)

对控制力矩约束式(27)与角速度约束式(32)进行校验可以得到

(41)

(42)

可以看到系统控制力矩约束与角速度约束能够同时得到满足。

本文所提出的变结构滑模控制器仿真结果如图9～图13所示。

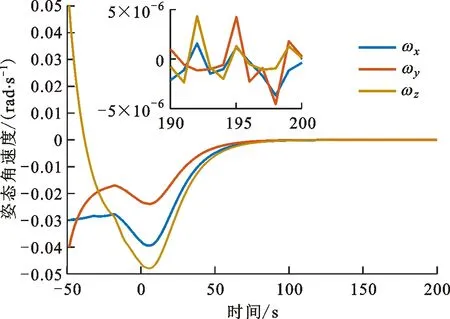
图9 变结构滑模控制器的姿态角速度曲线

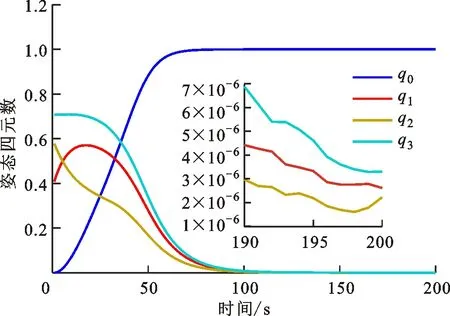
图10 变结构滑模控制器的四元数曲线

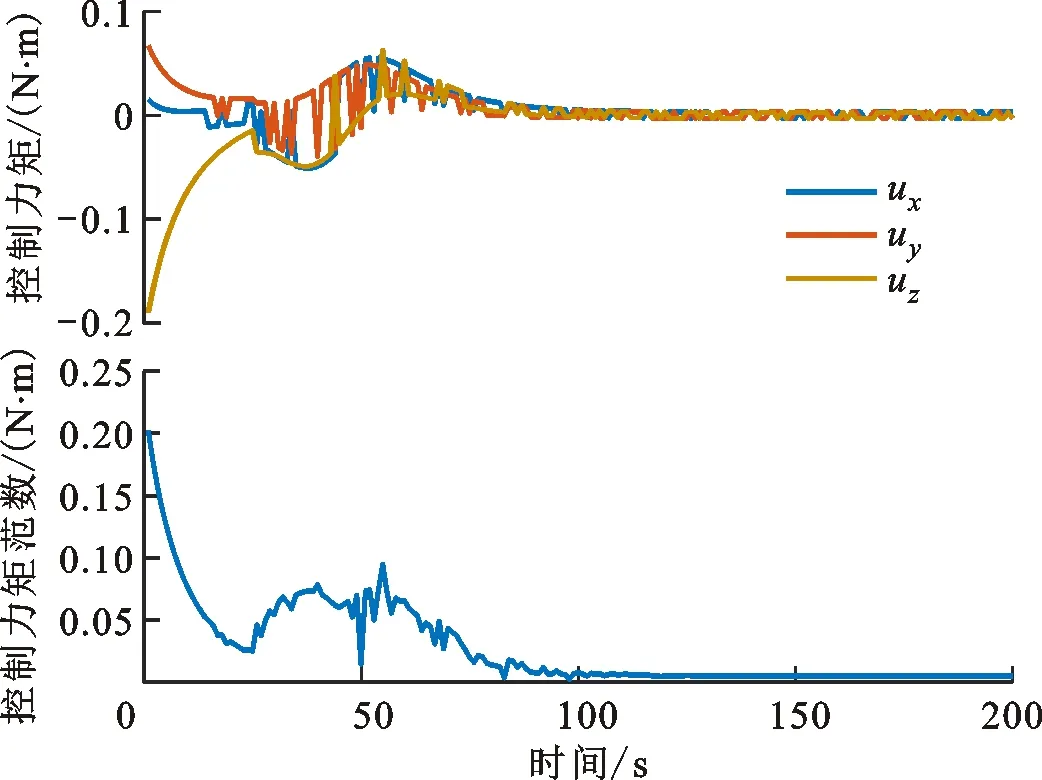
图11 变结构滑模控制器的控制力矩及其范数曲线

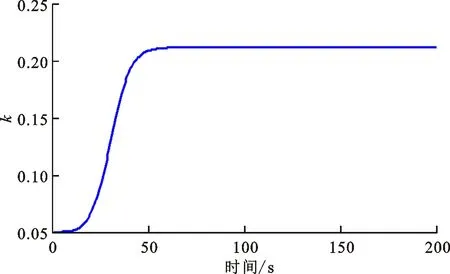
图12 变结构滑模控制器的滑模参数曲线

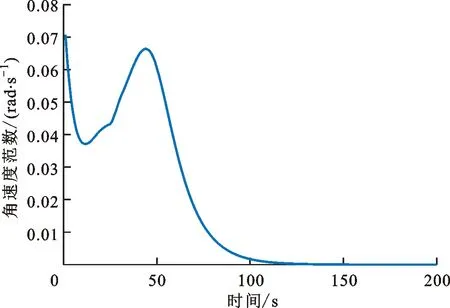
图13 变结构滑模控制器的角速度范数曲线

由图9、图10可以看出,系统在控制器作用下稳定收敛,且收敛时间约为105 s,与经典滑模控制器(38)(k=0.05)收敛时间相比有大幅度提升,这表明本文所提出的变结构滑模控制器收敛速率明显优于经典滑模控制器。同时由图9、图10可以看出,系统角速度与四元数的稳态精度为5×10-6rad/s与6×10-6,系统稳态精度仍然维持在较高的水准。但由图11、图13可以看出,系统控制力矩与角速度范数全程不超过系统上界,这证明了本次研究所提出的控制参数约束的有效性,并避免了控制力矩饱和与角速度饱和带来的一系列问题。同时由图12可以看出,滑模参数从初始值0.05开始逐步更新、放大,最终达到0.16左右,也正是滑模参数的实时放大避免了系统姿态角速度的过快下降,进而系统在滑模面上维持了较快速度的收敛速率,由图13的角速度范数曲线中也可以看出,在系统状态到达滑模面之后,系统姿态角速度有一个明显的先增后减的过程,这也是本文所设计的变结构滑模控制器的核心思路。

由控制器设计过程可以看到,主要影响系统收敛速率的是滑模初始参数k(0)与滑模更新参数p,二者选取较大的值能够带来更快地收敛速率,同时系统能够更加有效地利用控制机构能力。为说明二者对系统收敛速率的影响,选取多组仿真初值并进行仿真,其结果如图14～图16所示。

图14 k(0)=0.05、p=0.15条件下四元数曲线

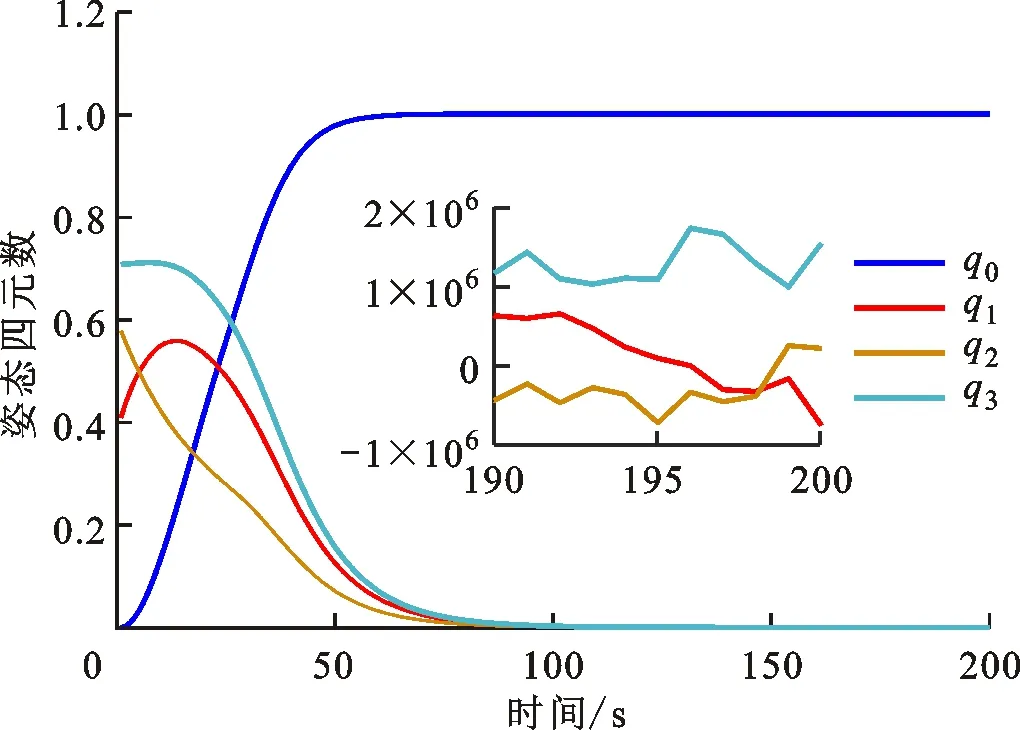
图15 k(0)=0.08、p=0.08条件下四元数曲线

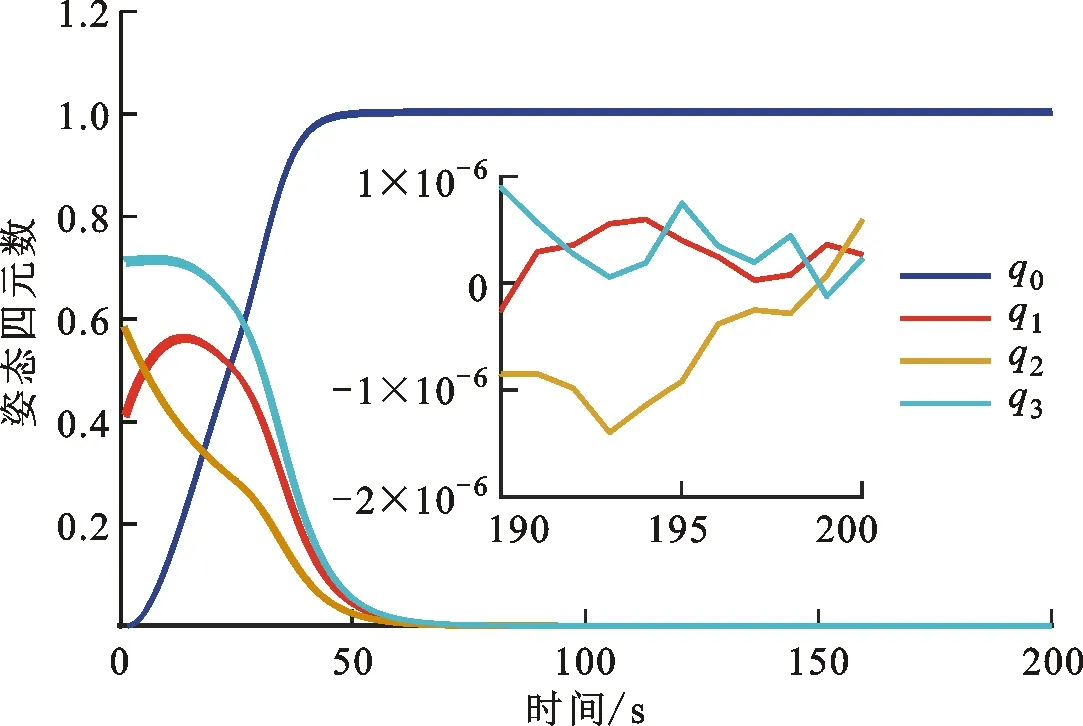
图16 k(0)=0.08、p=0.25条件下四元数曲线

可以看出,3组收敛时间分别为90 s、95 s与70 s,分别相比较于第一组变结构滑模控制的收敛速率都有所提升,这样说明增大滑模初值与其更新参数均能够提高系统收敛速度,但值得注意的是,在这3组仿真中只有前两组满足系统角速度约束亦即角速度未超过系统上界(严格参数约束式(32)已经不满足),最后一组系统角速度已超过系统上界,这也说明需要在系统收敛速率与性能约束之间进行合理平衡。

由表1所示的对经典滑模控制器与变结构滑模控制器的对比可以看出:同样条件下变结构滑模控制的收敛速率远大于经典滑模控制;不同条件时在基本维持变结构滑模控制的收敛时间与经典滑模控制在同一水平的前提下,系统的稳态精度仍然与经典滑模控制器保持在同一水平,但本文所提出的变结构滑模控制器解决了系统控制力矩饱和与角速度饱和的缺陷,并有效地提升了控制系统的收敛速率。

表1 经典滑模控制器与变结构滑模控制器对比

6 结 论

本文基于经典滑模控制器提出了一种变结构滑模控制器,在维持原有经典滑模鲁棒性强、物理特性明确的优势下,通过设计动态滑模面与滑模参数更新律,进而提高了系统的收敛速率,解决了经典滑模控制器中存在的收敛速率较慢的缺陷。此外还解决了当控制系统对收敛速率有较高要求时,经典滑模控制的控制力矩和姿态角速度因k增大而带来的其各自超过上界的问题。

研究结果表明,通过对于滑模参数的实时放大与更新,能够在初始滑模参数较小的前提下,有效避免系统角速度下降过快而带来的缺陷,从而实现对于系统收敛速率的改良,进而提升系统在平衡点附近的性能。值得注意的是,该研究所采用的方法均考虑的是最极端情形,这也意味着系统性能没有得到完全利用,而这也是作者在后续研究中需要重点解决的。