全捷联光电导引头的高动态解耦方法

陈 兵，李克勇，陈国良

(上海机电工程研究所，上 海 201109)

0 引 言

采用传统导弹对付非传统目标和软目标的效费比太低，且在城市战场和反恐战争中对付点目标情况下还会带来较大的附带毁伤。小型化低成本的导弹因其效费比高、能实现外科手术式精确打击而得到各国的重视[1]。鸭式双通道控制的气动布局、微惯性测量单元(miniature inertial measurement unit，MIMU)、全捷联光电导引头进行组合，是实现导弹低成本和小型化设计的重要途径之一[2]。随着MEMS技术、焦平面阵列(focal plane array，FPA)探测器技术和数字信号处理能力的发展，对于机动性要求不高的导弹，采用全捷联光电导引头进行目标探测和制导已成为可能。为了提高制导精度，该类导弹多采用比例导引方式，但捷联导引头无法直接获取比例导引所需的视线角速度，因而，惯性视线角速率的重构及滤波已经成为微小型捷联导弹需要攻克的几个主要关键技术之一[1]。

针对捷联式光电制导导弹，国内外学者提出了采用附加速率补偿的方法进行单通道视线角速率重构[3]，利用抖动自适应加滤波与微分网络形成视线角速率[4]，利用扰动观测器估计视线角速率[5]，采用扩展Kalman[6]与无迹Kalman[7]滤波技术估计惯性视线角速率等方法。但上述方法只适用于弹目相对运动关系已知或导弹只进行小过载机动的情况。

本文以某类微小型光电制导导弹为研究对象，其特点为：目标探测传感器与弹体固连，输出弹轴与弹目视线的夹角；MIMU与弹体捷联，输出弹体姿态角速度和弹体姿态；弹体在4片鸭舵控制下进行俯仰偏航机动，同时绕纵轴连续滚转。导弹采用比例导引实现对运动目标的高精度拦截，由于弹体姿态变化快，跟踪解耦提取视线角速度的方法难以达到精度要求。因此，本文提出一种基于Kalman滤波的数字解耦算法，解决弹体旋转等高动态带来的捷联解耦问题，并通过数值仿真验证了该方法的可行性。

1 坐标系定义

射击坐标系Axyz：坐标原点A为导弹发射时刻质心位置；Ax在水平面内，指向目标运动方向的反方向；Ay铅垂向上；Az根据右手定则确定。

弹体坐标系Ox1y1z1：坐标原点O为导弹质心；Ox1与导弹纵轴重合，指向前为正；Oy1位于弹体某一纵向对称面内，弹体平放时指向上为正；Oz1根据右手定则确定。

视线坐标系O1xsyszs：坐标原点O1为导引头视场中心；O1xs与导弹-目标连线重合，指向目标为正；

O1ys位于O1xs所在铅垂平面内，垂直于O1xs，指向上为正；O1zs根据右手定则确定。

体视线坐标系O1xtytzt：坐标原点O1为导引头视场中心；O1xt与导弹-目标连线重合，指向目标为正；O1zt位于弹体坐标系Ox1z1平面内，并垂直于O1xt；O1yt与O1xt、O1zt组成右手坐标系。

各坐标系的关系如图1所示[8]。

图1 坐标系转换关系Fig.1 Coordinate systems transformation relationship

则有

(1)

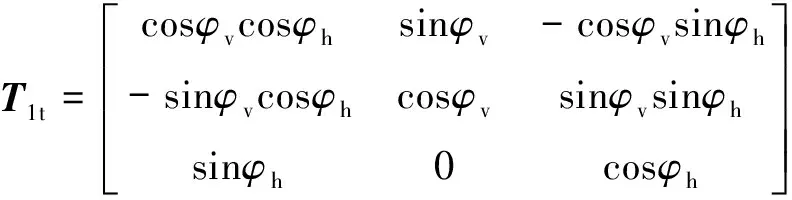
(2)

(3)

(4)

式中：Τ01为射击坐标系到弹体坐标系的转换矩阵；T1t为弹体坐标系到体视线坐标系的转换矩阵；Tts为体视线坐标系到视线坐标系的转换矩阵；T0s为射击坐标系到视线坐标系的转换矩阵；ψ、ϑ、γ为弹体姿态角；φh、φv为目标方位角；qh、qv、γq为弹目视线角。

2 传统跟踪解耦算法

传统的跟踪解耦算法根据弹上MIMU测量的弹体角速度信息构建跟踪解耦平台进行解耦[9]。跟踪解耦原理框图如图2所示。

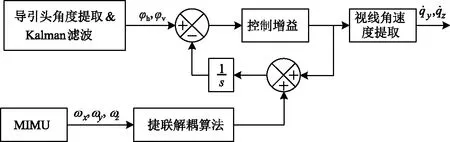
图2 跟踪解耦原理框图Fig.2 Tracking decoupling block diagram

3 数学解耦算法

3.1 数学解耦原理

数学解耦提取视线角速度的原理框图如图3所示。

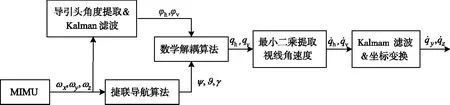
图3 数学函数解耦原理框图Fig.3 Mathematical function decoupling block diagram

射击坐标系到体视线坐标系的转换矩阵有如下2种表达形式。

(5)

(6)

式中：

(7)

由此可得

qv=arcsin(C12)

(8)

(9)

(10)

则可得体视线系下的视线角速度为

(11)

3.2 导引头视线角提取

对于全捷联光电导引头，目标在导引头视场中的位置如图4所示。通过Δx1,Δy1,Δz1即可解算出弹轴与弹目视线的夹角φh,φv。

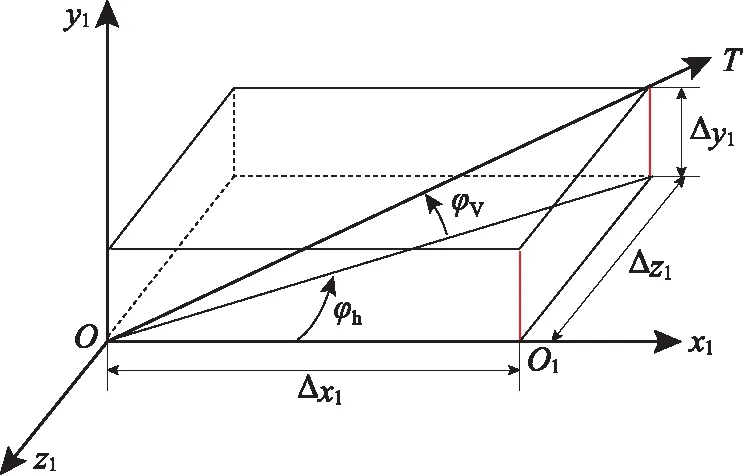
图4 全捷联光电导引头测角原理Fig.4 Angle measurement principle of strapdown photoelectric seeker

(12)

采用Kalman滤波获得φh、φv的基本方程为

(13)

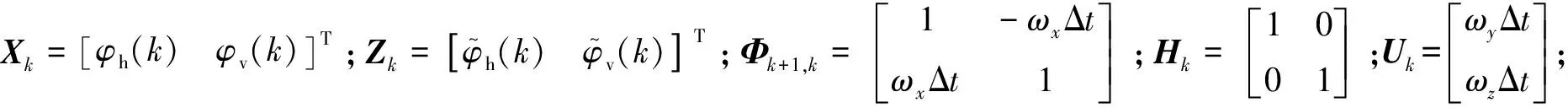
3.3 弹体姿态角解算

弹载MIMU可以输出弹体的姿态角或姿态角速度。当输出仅为姿态角速度时，需通过式(14)积分获得姿态角或者采用四元数旋转双子样算法解算姿态[10]。

(14)

3.4 视线角速度提取

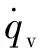
(15)

式中：a、b分别为线性项和零次项的系数。

(16)

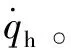
4 数值仿真分析

在弹体非旋转和旋转条件下采用跟踪解耦方法进行数值仿真，得到视线角速度曲线分别如图5和图6所示。由图可知，当弹体非旋转时，跟踪解耦能够输出较好的视线角速度；当弹体旋转时，解算的视线角速度存在严重的延时和衰减。因此，该方法用于鸭式双通道控制的捷联光电制导导弹提取视线角速度时存在困难。

图5 无滚转时导引头视线角速度输出(跟踪解耦)Fig.5 Line-of-sight angular velocity output without roll (tracking decoupling)

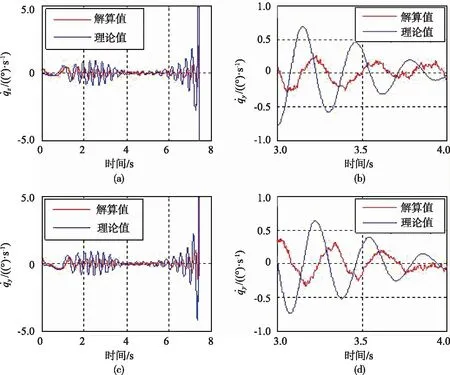
图6 弹体3 r/s滚转时导引头视线角速度输出(跟踪解耦)Fig.6 Line-of-sight angular velocity output with roll rate of 3 r/s (tracking decoupling)

采用本文提出的数学捷联解耦方法进行数值仿真，仿真结果如图7～10所示。其中，导引头框架角叠加了0.1°(3σ)的测量随机噪声。由图可见，在弹体旋转和非旋转情况下，解算输出的视线角速度以及导引头测角均与理论值吻合很好。

图7 无滚转时导引头测角输出Fig.7 Seeker angle output without roll

图8 无滚转时视线角速度解算输出Fig.8 Line-of-sight angular velocity output without roll

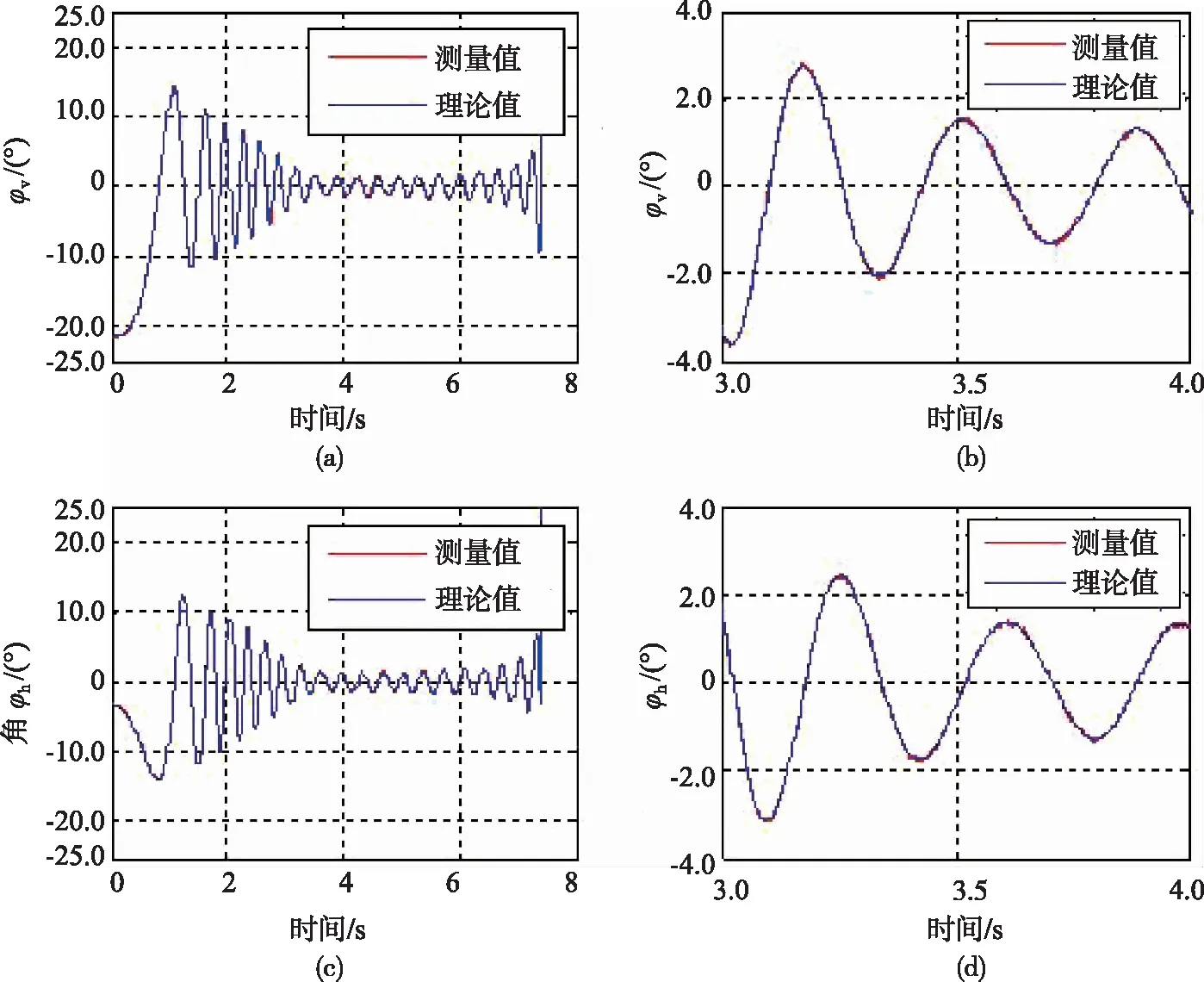
图9 弹体3 r/s滚转时导引头测角输出Fig.9 Seeker angle output with roll rate of 3 r/s

图10 弹体3 r/s滚转时视线角速度解算输出Fig.10 Line-of-sight angular velocity output with roll rate of 3 r/s

5 结束语

本文提出了一种微小型光电制导导弹的捷联解耦方法。该方法基于弹体姿态角和导引头测角输出，通过数学方法解算惯性空间视线角，采用最小二乘拟合获取视线角速度，并将惯性系视线角速度转到弹目视线系中，以实现捷联制导与控制。该方法避免了弹体旋转等高动态因素引起的捷联解耦困难。数值仿真结果表明，本文提出的数学解耦方法能够准确输出视线角速度，相比跟踪解耦方法，具有更好的适应能力。