基于动态逆的空天变体飞行器姿态控制

万 航，徐胜利，张庆振，张 迪

(1. 北京航空航天大学 自动化科学与电气工程学院，北京 100083；2. 上海机电工程研究所，上海 201109)

0 引 言

对于采用后掠机翼的高超声速飞机，高速和低速性能要求相互矛盾。大后掠角虽然可以降低激波阻力，有利于跨声速和超声速飞行，但是也带来诱导阻力大、低速特性差的问题[1]。面对现代高超声速飞行器飞行包线大、作战任务复杂的特点，需要具有可变几何形状机翼的气动布局，典型的方案就是机翼后掠角可以为适应飞行环境而主动变形。可变后掠翼布局是指在飞行过程中机翼后掠角可以随飞行速度变化而改变的气动布局。变后掠翼飞机最大的优点在于飞行中可以通过改变机翼后掠角来改善飞机升力、阻力特性，使飞机飞行性能在高速和低速情况下都能得到优化[2-3]。

但是，外形切换必然导致诸如气动参数、质心和转动惯量等系统关键参数的变化，同时考虑多刚体力学原理，各刚体之间必然存在复杂的相互作用力，惯性耦合、运动耦合强烈，这些都对飞行器姿态稳定控制提出了挑战。文献[4]针对一类变外形飞行器设计线性变参数(linear parameter varying，LPV)姿态稳定控制系统，基于多胞形定理设计顶点控制器并利用权重矩阵进行控制分配从而完成整个飞行包线的稳定控制。文献[5]针对变外形飞行器将LPV系统与鲁棒控制思想结合起来，研究了LPV系统的H∞变增益控制。文献[6]使用鲁棒动态逆的控制方法对高超声速再入飞行器的控制问题进行了研究。

从国内外研究现状看，目前对于变外形飞行器的研究多集中于对飞行器纵向运动进行稳定控制，大多忽略了具有强烈耦合特性的横侧向通道，缺乏对六自由度模型的姿态控制研究，也未对高超声速条件下进行外形切换所产生的不确定性对控制系统的影响进行研究。

本文针对变后掠飞行器在变外形过程中的稳定控制问题，利用Kane方法建立了考虑多刚体相互作用机理以及变外形动态作用机制的动力学模型，基于固定构型设计稳定控制器，利用ESO观测补偿变外形过程中的不确定项以及干扰项，保证过渡过程的控制稳定，并进行了仿真验证。

1 空天变体飞行器动力学模型的建立

在保留模型主要特性的条件下，为了简化问题的复杂性，需要对飞行器及其飞行环境做出以下假设。

1) 假设飞行器机体和机翼均为刚体，飞行过程中质量均保持不变；

2) 翼身连接点到机翼任意点的距离保持不变，即保证机体和机翼的连接；

3) 机翼只能水平转动，不能垂直转动；

4) 机翼为均匀质矩形薄面，不考虑翼型带来的影响。

模型也不考虑控制设备和执行机构的动态特性。在变体方式主要为变后掠角的情况下，将对象飞行器简化，如图 1所示，各坐标系定义与传统苏式坐标系定义相同[7]。

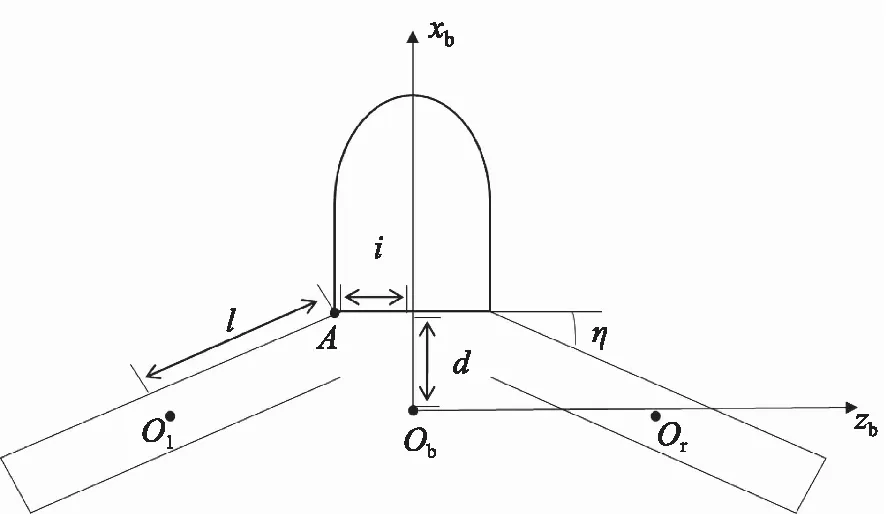
图1 空天变体飞行器模型简化图Fig.1 Schematic diagram of aerospace morphing vehicle model

飞行器被简化为三个刚体：机身、左右机翼。机身质心为Ob；左右机翼质心分别为Ol、Or，左机翼可绕翼身连接点A转动，变形方式为对称变形；d、i分别为机身质心到左翼身连接点A的纵向(xb方向)距离和侧向(zb方向)距离；l为翼身连接点到机翼质心的距离；η为左右机翼的前缘后掠角。

利用基于逆的思想设计控制器，需要保证对象模型相对精确，本文采用适用于多刚体建模机制的Kane方法建立无动力空天变体飞行器动力学模型。为便于控制系统设计与分析，其仿射型表达如式(1)所示。

(1)

系统的状态量为三通道气流角和姿态角速率：x=[α,β,γV,ωx,ωy,ωz]T；系统的控制量为升降舵、方向舵和副翼舵偏角：u=[δe,δr,δa]T；系统依赖项如式(2)所示。

(2)

式中：

(3)

式中：v表示系统质心运动速度；L、C分别表示飞行器所受升力和侧力；θ、ψV分别表示弹道倾角和弹道偏角；Lβ、Nβ分别为滚转力矩和偏航力矩关于侧滑角的系数；M0、Mα分别表示俯仰力矩基准值和俯仰力矩关于攻角的系数；Jbx、Jby、Jbz为机身的转动惯量；mT、ml、mr分别表示飞行器质量和左右后掠翼质量；c表示机翼质心在yb方向的偏置；Δ1、Δ2、Δ3为变后掠产生的附加力矩。

控制矩阵如式(4)所示。

(4)

式中：Lδr、Lδa分别为滚转力矩关于方向舵和副翼的系数；Nδr、Nδa分别为偏航力矩关于方向舵和副翼的系数；Mδe为俯仰力矩关于升降舵的系数。

2 基于动态逆的控制器设计

2.1 姿态控制模型转换

根据姿态运动方程(1)，我们定义Δα=α-αT和Δδe=δe-δeT，分别为攻角α与平衡攻角αT的差值、升降舵偏δe与配平舵偏δeT的差值。对于无动力再入飞行器，平衡攻角αT一般与马赫数有关，对于姿态稳定回路来说，马赫数为长周期变量，本文将平衡攻角αT视为常量，δeT为对应的配平舵偏。

同时，我们将弹道倾角θ、重力加速度g等长周期变量视为常量。根据受力分析，可以忽略舵偏角对升阻侧力的影响，并且将气动力矩系数在平衡点附近做线性化展开，便于系统的仿射型表达。对于系统线性化近似所带来的模型误差将会在控制律设计中加以考虑，从而保证局部稳定性。

对于无动力再入飞行器，气流角是再入过程中的关键变量，而再入过程中纵向通道一般采用配平攻角，所以在设计控制器时我们选择攻角相对于平衡点的变化量Δα、侧滑角β和倾侧角γV作为系统输出，即

y=[α-αT,β,γV]T=[Δα,β,γV]T

(5)

相应的控制量为升降舵相对于平衡点的变化量、方向舵和副翼舵偏角。为了能够得到系统输出和控制量的线性化关系，我们采用文献[8]的方法，对系统每个输出求其高阶微分项直到其微分方程中显式地含有控制量，用ri来表示上述方法中第i个输出的最小微分阶数，定义与所选输出相关的系统相对阶数r为

(6)

基于输入输出线性化思想设计的控制器性能都依赖于非线性系统的内动态稳定性。如果系统的相对阶数与状态量维数相等，就不会存在不稳定的内动态，就可以基于线性化模型设计控制器；否则，非线性系统仅仅只能部分线性化，其稳定性是由线性化后的系统和内动态两者共同决定[9]。

考虑本文所研究对象，系统输出攻角、侧滑角和倾侧角都需要分别求二阶微分才可以显式地包含控制量。因此，系统的相对阶数与状态量维数相同，线性化后的模型可以完整地表达原非线性系统的所有动态，不存在不稳定的内动态。

(7)

(8)

(9)

(10)

2.2 基于动态逆的控制器设计

改写2.1节得到的线性化系统，将控制量显式表达，得到正则表达式，如式(11)～(13)所示。

(11)

(12)

(13)

用矩阵形式表示式(12)，有

(14)

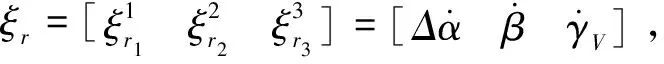
u=A-1(ξ)(-B(ξ)+vs)

(15)

式中：vs为虚拟控制量，包含一个比例反馈校正环节和指令的微分，指令的微分可以用文献[10]所述的跟踪微分器(tracking-differentiator，TD)对指令信号求取微分获得。将指令信号yic代入其中，可以得到跟踪微分信号如式(16)～(17)所示。

x1→yic

(16)

(17)

将上述控制律代入系统方程(12)，得到响应形式如式(18)～(19)所示。

(18)

(19)

只要控制指令的微分求取正确，yi就会跟踪对应的指令信号。

2.3 基于ESO的衔接控制器设计

空天变体飞行器在外形切换过程中，其多刚体内部作用机理存在不确定扰动项，外界环境也会产生很大的干扰力矩，这些动态过程无法被精确建模。在系统方程中，如式(2)所示，内环角速度微分方程中的Δ1、Δ2、Δ3即为系统的广义总和扰动，本文采用基于ESO的干扰观测技术[11]，将外形切换过程中的时变参数作为干扰量，对其进行观测和补偿，从而达到稳定过渡的控制效果。

(20)

设计状态观测器

(21)

式中：zi1，zi2，zi3为系统状态量的估计值；βi1，βi2，βi3为观测器增益系数。

最终实现观测结果

zi1→yi

(22)

(23)

(24)

将状态观测器估计的扰动值作为前馈补偿项加入式(15)中，得到基于ESO的衔接控制律为

u=A-1(ξ)(-B(ξ)-ξ′+vs)

(25)

3 仿真试验

3.1 固定构型稳定控制仿真

为验证控制器性能，对本文所设计控制器在固定构型下进行仿真，仿真结果如图2～4所示。仿真初始条件为：后掠角60°，高度50 km，速度5Ma，攻角6°，跟踪4°阶跃指令，侧滑角和倾侧角为0°，侧滑角保持0°，倾侧角跟踪20°阶跃指令。由于系统方程呈现出高阶非线性特性，仿真时，对阶跃指令进行平滑处理，防止仿真初始时刻较大的误差对系统稳定性造成不利的影响。

由图2～4可以看出，攻角和倾侧角都可以在4～5 s内实现对指令的无超调跟踪，侧滑角则很好地稳定在0°附近，初始跟踪阶段存在容许偏差内的微弱振荡。

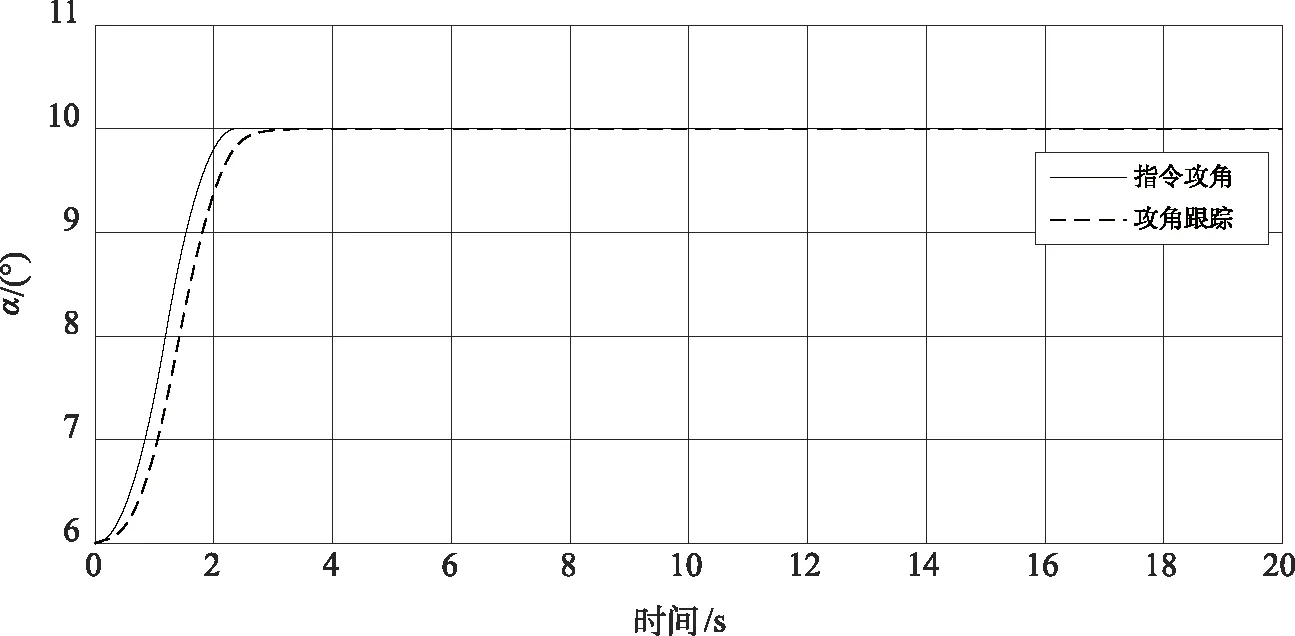
图2 固定构型攻角跟踪曲线Fig.2 Angle of attack tracking curve of fixed configuration

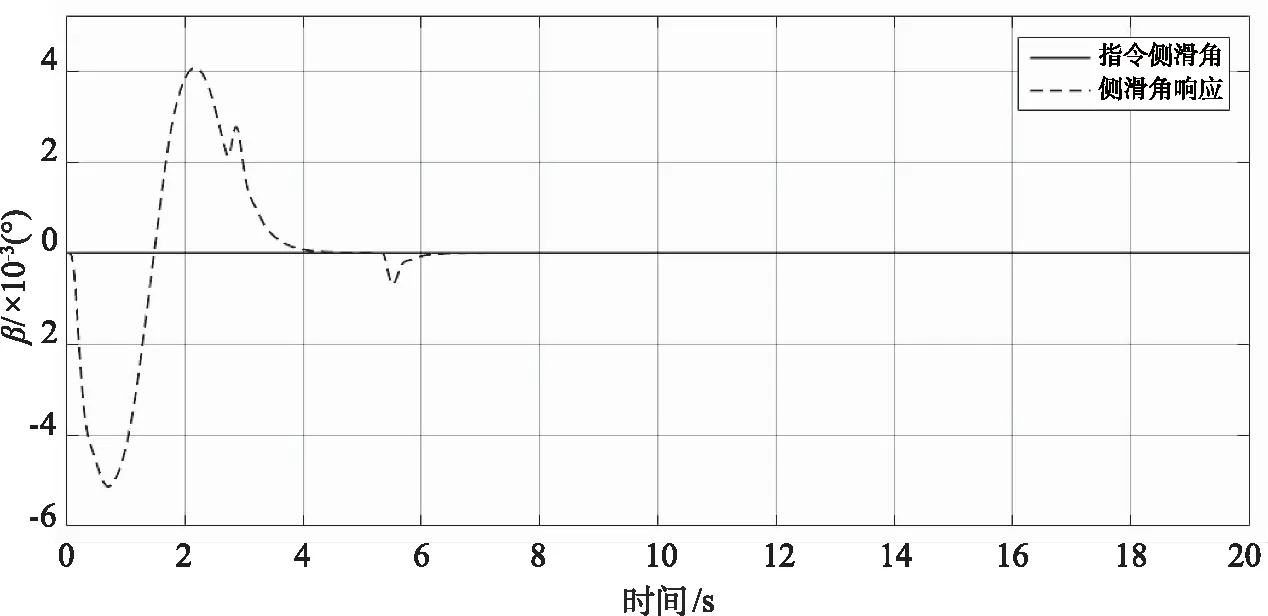
图3 固定构型侧滑角跟踪曲线Fig.3 Angle of sideslip tracking curve of fixed configuration

图4 固定构型倾侧角跟踪曲线Fig.4 Bank angle tracking curve of fixed configuration

3.2 衔接控制仿真

为验证变外形阶段衔接控制器的控制性能，在其余初始条件不变的条件下，设定后掠角变化的角速度为1 (°)/s，后掠角从基础状态的50°增加到60°，保持5 s，然后再增加到65°。攻角指令为方波信号，分别在初始时刻和变后掠结束时刻进行指令切换，侧滑角和倾侧角指令不变。将控制结果与未加ESO控制器的仿真结果进行比较，如图5所示。

(a) 攻角跟踪对比曲线

(b) 侧滑角跟踪对比曲线

(c) 倾侧角跟踪对比曲线图5 过渡过程姿态角跟踪曲线Fig.5 Attitude angle tracking curve of transition process

图5(a)给出了两种控制器作用下系统对方波指令的响应曲线，可以看出，相较于动态逆控制，衔接控制器具有更小的超调量，并且稳态误差基本为零。而动态逆控制由于无法消除变外形过程中的干扰力矩，具有较大的稳态误差。由图5(b)可以看出，侧滑角控制效果方面也可以得出相同的结论，基于ESO的衔接控制器可以有效抑制扰动，对干扰力矩具有一定的鲁棒性。

4 结束语

本文针对无动力空天变体飞行器的稳定控制问题，提出了一套适用于变体飞行器的姿态稳定控制律设计方法。通过Kane方法建立考虑飞行器多刚体相互作用机理的动力学模型，基于精确模型设计动态逆控制器。理论推导和仿真试验表明，系统不存在不稳定内动态，可以实现对指令的良好跟踪。针对外形切换可能导致的干扰问题，设计基于ESO观测补偿的衔接控制器，仿真结果表明，所设计控制器能够实现过渡过程的稳定控制。