光电二维探测系统中基于视线距离的数据关联算法研究
2019-12-18王鑫亮蔡卫峰邱令存原爱华
王鑫亮,蔡卫峰,邱令存,原爱华,曹 政
(1. 南京理工大学自动化学院,江苏 南京 210094;2. 上海机电工程研究所,上海 201109)
0 引 言
现代化战争对作战平台的隐身性、战场情报的全方位和实时性等要求越来越高,光电探测系统作为航空电子技术的重要组成部分,成为各国竞相发展的高新技术[1]。不过光电二维探测系统仅能探测到目标的方位角和俯仰角,即目标视线(line-of-sight,LOS),属于被动跟踪。被动传感器系统需要多个观测站相互协作才能对空间目标进行定位。它通过高精度的测向设备在多个观测点对目标进行测向,各个测向线的交点就是目标的位置,在该过程中需要解决的一个重要问题就是测量数据关联问题,也就是确定哪些测量值来源于同一目标,即同一性识别问题。然而由于噪声的存在,解决噪声情况下的数据关联问题就成为了许多研究者研究的重点。
通常被动多传感器数据关联可以描述为多维分配问题,用穷举法求其最优解是 NP-hard 问题,计算复杂度随问题维数的增加呈指数增长[2-4]。由于其过于巨大的存储和计算要求,实际系统中很少采用这种方法。还可以采用基于角度余切值的关联算法[5],该方法直接利用角度信息,构造检验统计量,然后通过方位角检测和俯仰角检测得到可能的候选关联集,进而采用指示函数法对候选关联集进行分析,挑选出正确的关联组合[6]。该方法仍然存在着计算量大与复杂等问题,不适用于光电系统。文献[7]的算法简单清晰,理论性强,很有可能适用于工程应用。对其进行系统的仿真与分析后发现(仿真结果与分析在下文中给出),在不存在噪声并且测量无误差的情况下,该方法确实简洁准确,然而当存在噪声时该方法的准确性将急剧下降,所以并不适用。在以上所有算法的启发下,本文提出了一种基于视线距离构建检验统计量的关联算法,该算法理论性强、易于理解、实用性强。通过大量仿真,证明本文所用方法的有效性与实用性。由于本项目主要应用于3部光电系统,故本文重点给出不同杂波下基于三站的仿真结果。
1 视线距离
在介绍视线距离之前,先了解方位角、俯仰角的概念以及本工程所用的坐标系,如图1所示。X轴表示正北方向;Z轴表示正东方向;Y轴表示高度;α表示方位角,也就是某点从北方向线起,依逆时针方向(偏正东方向)到目标方向线之间的水平夹角;β表示俯仰角,也就是目标相对于XOZ坐标系平面的“俯仰”的角度;R表示空中飞行的目标。下文中给出了视线距离的概念。
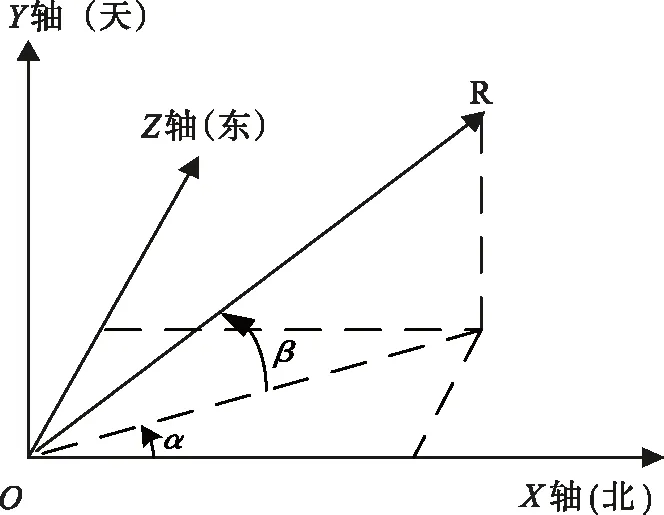
图1 坐标系规范图Fig.1 Standard diagram of coordinate system

(1)
(2)
(3)
(4)
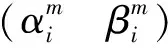
(5)
如图2所示,在存在测量误差和噪声的情况下,两直线不会相交,

图2 视线距离示意图Fig.2 Schematic diagram of line-of-sight distance
2 关联算法
2.1 时空对准
各部光电探测器针对共同的目标会得到不同步的测量信息,时间配准的任务是将这些信息同步到相同的时间点上。为了获得可靠的目标测量值,需要将全部传感器的局部测量值转换到相同的坐标系中,通过多部光电探测器对空间内相同目标的测量完成传感器系统偏差的估计和补偿,从而完成空间对准。具体方法如下。
在进行时空坐标统一时,先采用三次样条函数进行采样点之间的函数拟合,然后通过函数插值的方法进行时空坐标的统一。
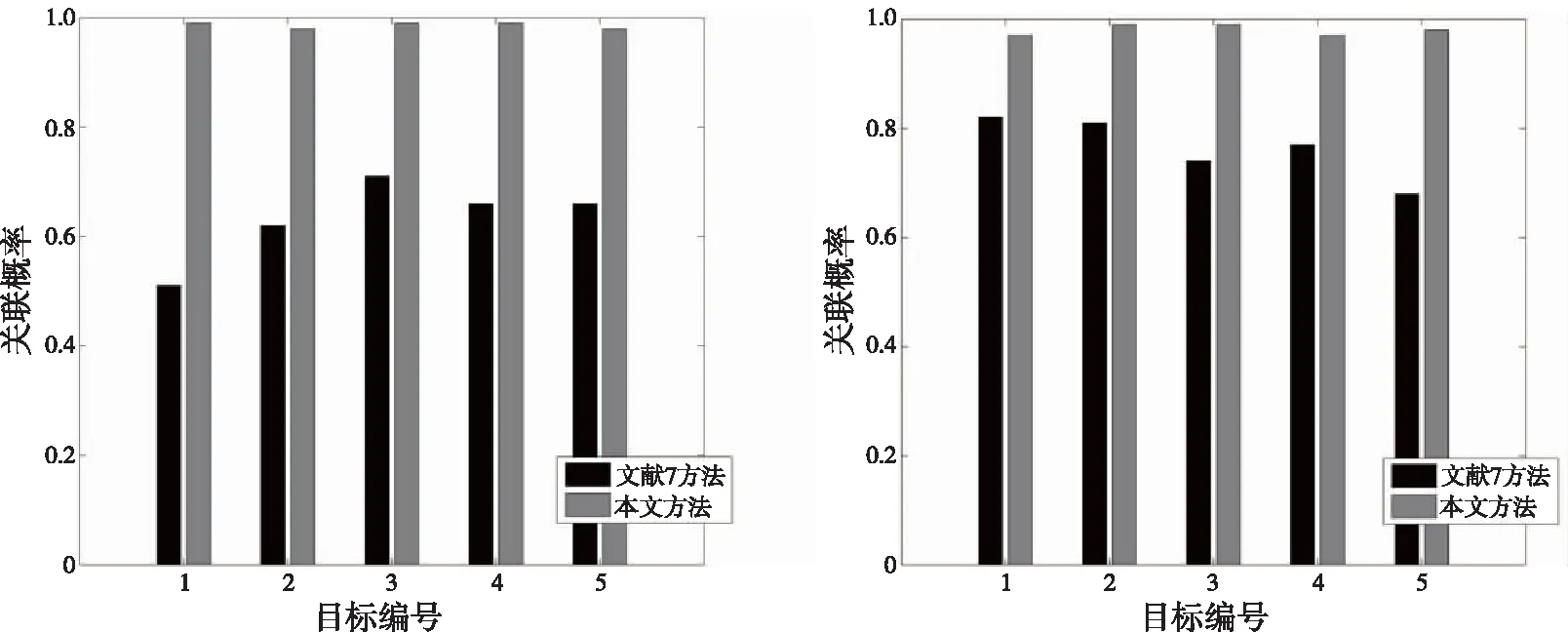
假设区间[a,b]上具有n个小区间Δ(a=t0 (6) 式中,Mi的计算式为 (7) 式中ai、βi和γi的取值为 (8) (9) (10) (11) 图3 时空对准示意图Fig.3 Schematic diagram of time-space alignment 在进行时空对准时,考虑到各个探测源的采样周期不同,需要将采样周期短的航迹向采样周期长的航迹对齐。 (12) (13) 由式(13)可以看出:代价函数为关联组合中任意两个测量值之间的视线距离之和,当各探测器的测量误差为0时,各部光电探测器对于同一个目标的视线便会相交于目标的位置点。当存在测量误差时,各部光电探测器对于同一个目标的视线之间的距离和应最短。这是本文判别是否关联成功的一项重要条件。 1) 步骤1 假设共有Ns部光电探测器,mn个目标,设置一个检验门限D(文献[7]方法与本文仿真的参考门限均由经验法所得),对探测到的数据进行时空配准。 2) 步骤2 3) 步骤3 4) 步骤4 5) 步骤5 6) 步骤6 下面以3部光电探测器、5个目标为例进行仿真计算,目标位置分为水平编队和十字编队,场景与文献[7]相同。 水平编队时,各目标位置为 十字编队时,各目标位置为 其中,d1和d2(d1=10 m,d2=2d1)表示目标间隔,也就是目标的空间分离度。给定这些初始目标在X、Y、Z方向的速度,模拟空中真实飞行的目标,3部光电探测器位置分别为(0,3 000,0),(3 000,0,0),(-3 000,0,0),按照一定的时间间隔探测出不同时戳下的目标测量值,然后对这些数据进行时空对准与同一性识别,完成关联。场景序号1~3表示不同系统误差设定值的3个场景,下面给出仿真计算结果。 表1 不同序号下的系统误差设定值Tab.1 System error settings under different sequence numbers 本文通过改变目标位置,在不同的噪声情景下进行大量的仿真。由于光电探测系统中的噪声瞬时值呈正态分布,同时它的功率频谱密度又是均匀分布的,因此仿真中的噪声为0均值的高斯白噪声(如表1所示,σα1、σβ1分别表示方位角和俯仰角的系统误差设定值)。图4~6中方位角误差σα2和俯仰角误差σβ2分别设定为1.0°、0.6°。本文对不同噪声下的情景分别进行100次的Monte Carlo仿真,通过分析比较得出结论。 分别对文献[7]的方法和本文的方法进行仿真,如图4~6所示。图4~6中,(a)图为目标水平编队结果图,(b)图为目标十字编队结果图,横轴上1~5表示目标1~5,纵轴表示正确的关联概率,图中列出了文献[7]方法与本文方法的对比仿真结果。 图4~6分别对应场景序号1~3的仿真结果。 (a) 目标水平编队结果 (b) 目标十字编队结果图4 场景序号1关联概率比较结果图Fig.4 Association probability comparison result graphs in Scenario 1 (a) 目标水平编队结果图 (b) 图为目标十字编队结果图图5 场景序号2关联概率比较结果图Fig.5 Association probability comparison result graphs in Scenario 2 (a) 目标水平编队结果 (b) 图为目标十字编队结果图6 场景序号3关联概率比较结果图Fig.6 Association probability comparison result graphs in Scenario 3 通过对文献[7]中的方法进行仿真可知,在未加入噪声的条件下,数据基本全部关联成功。而加入噪声后,随着噪声的增大,由文献[7]方法得出的关联概率不断下降,而由本文方法得出的关联概率较高且基本保持稳定。分析图4~6可以得出: 1) 当目标空间分离度大时,关联概率会有一定的提升,与文献[7]得出的结论一致。 2) 当噪声较小时,关联概率基本不会受到影响;随着噪声的增大,由本文方法得出的关联概率较高且基本保持稳定。 3) 在有噪声的情况下,本文方法具有较强的适用性,能够满足工程应用需求。 本文提出了一种适用于存在杂波情况下的基于视线距离的被动多站多目标数据关联算法,详细地阐述了在不同噪声下算法的适用性,通过构建检验统计量取代仅基于视线距离的关联算法,具有较强的理论意义,并通过仿真验证了该算法的有效性。然而该算法仍存在一定问题,在目标分离度较小的情况下,该算法得出的关联概率偏低,后续研究中需不断对本文算法进行改进,从而达到适用于任意场景的效果。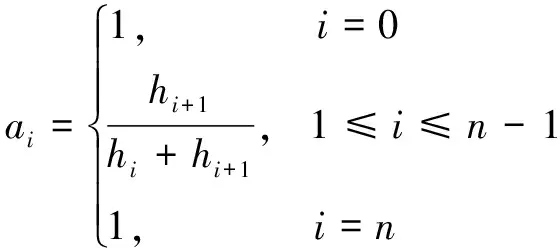
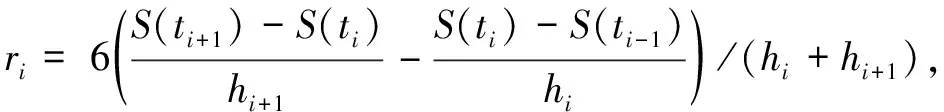
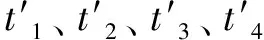
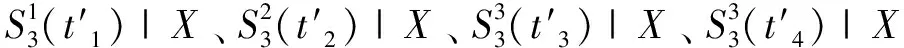

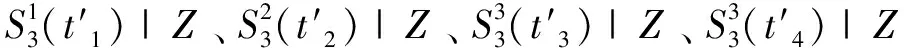
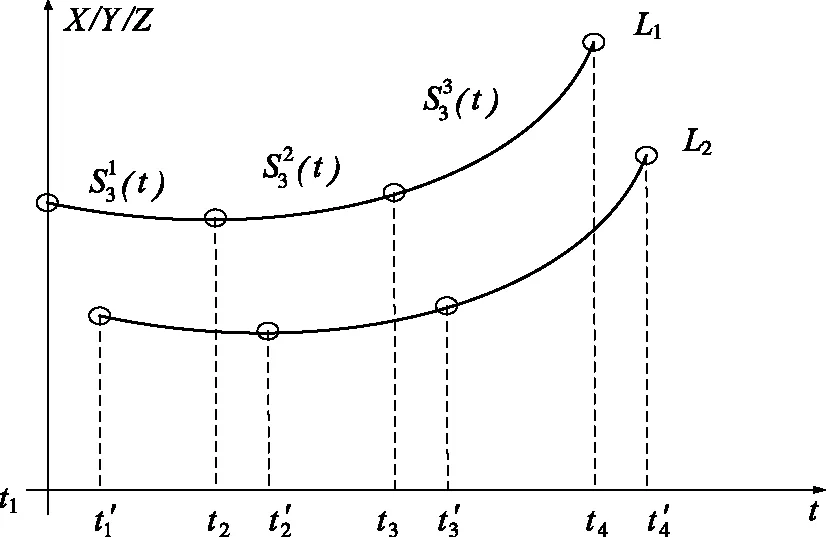
2.2 检验统计量


2.3 代价函数
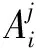
2.4 具体算法流程
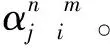
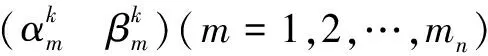
3 仿真计算与结果分析
3.1 仿真场景
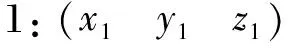
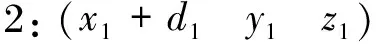

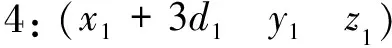
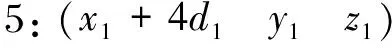
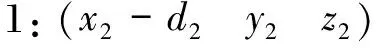
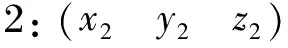
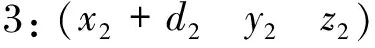
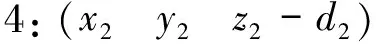


3.2 仿真结果


3.3 结果分析
4 结束语
