基于改进K均值聚类的战术导弹试验数据分析

黄伟恺，马 行，刘 进，李宇平，郑丹力

(上海机电工程研究所，上海 201109)

0 引 言

开展战术导弹振动及应力筛选试验时，通常是在比较宽的频率范围内对导弹施加振动，使导弹的多个共振点同时受到激励而产生共振，从而发现扭曲、碰撞等作用可能对导弹造成的损坏，尽早暴露产品的早期设计缺陷。因此，针对战术导弹的振动及应力筛选试验开展试验数据分析工作，可以为战术导弹的研制以及相关测试系统的改进提供分析依据或建议。

在试验数据中，由于系统误差、人为误差或者数据变异等原因，部分试验数据与总体试验数据的行为特征、结构或者相关性不一致，则称该部分试验数据为异常试验数据。通常，对异常试验数据的筛查方法主要包括：基于统计的方法[1]、基于距离的方法[2]、基于偏度的方法[3]以及基于聚类的方法[4]。其中，聚类方法的复杂度低、效率较高，比较适用于数据量较大的异常试验数据筛查。

K均值聚类算法在数据挖掘领域应用较为广泛，但是，基本K均值算法在具体工程应用上有一些局限性，例如初始聚类中心选择的随机性、容易陷入局部最优等。很多学者致力于解决基本K均值聚类的缺陷：①陶莹[5]采用全局化思想改进了K均值聚类算法，通过对比分析验证了算法的稳定性，但是没有解决K=1时初始聚类中心的随机性问题，并且算法迭代过程效率不高；②马晨光[6]建立了基于遗传K均值算法的聚类分组模型，实现了聚类过程分组数目的自动学习，但没有实现异常数据的检测；③陈永波[7]改进了K均值聚类初始聚类中心的选取方法，在一定程度上解决了局部最优的问题，提高了动态心电分析的准确性和效率，但是所提出的改进K均值聚类算法不具备普适性；④由于试验数据是典型的时间序列，霍纬纲[8]提出了一种基于升力系数 (lift ratio, LR)分量提取的多维时间序列 (multivariate time series, MTS)聚类算法，采用K均值算法对模型向量集进行聚类分析；⑤张乾君[9]针对多雷达数据融合问题，提出了基于时间序列的模糊聚类算法，解决了跟踪目标较多算法效率低的问题。

本文针对战术导弹振动及应力筛选试验数据的分析和处理问题，对K均值聚类算法的缺陷进行分析，以期从大数据量的试验数据中发现蕴含价值的潜在规律，从而实现战术导弹试验数据的自动化处理和分析。

1 K均值聚类算法原理和局限性分析

1.1 K均值聚类算法的基本原理

K均值聚类算法的基本原理如下：

1) 随机指定K个数据点作为算法的初始簇中心；

2) 计算数据集中所有数据点与初始簇中心的相似度，把各个数据点归入最相似的簇；

3) 根据被归入的数据点，重新计算各簇中心；

4) 反复迭代2)、3)，至满足收敛条件。

K均值聚类算法复杂度低，若以欧氏距离作为数据点的相似度测度，算法复杂度可表达为O(t·K·n·d)。其中：n为数据集的大小；K为聚类中心个数；d为数据的维度；t为迭代次数。通常，取t、K、d为常量，所以算法复杂度可简化为O(n)。

1.2 K均值聚类算法的局限性

K均值聚类算法存在以下缺陷：

1) 随机选择的初始簇中心对聚类结果影响巨大。如图 1所示，(a)和(b)对应的聚类结果较(c)和(d)对应的聚类结果要好，这是因为(a)和(b)所选择的初始簇中心更接近真正的簇中心。通过上述对比可知，选择初始簇中心不合适会导致聚类结果存在较大误差。

2) 异常试验数据对聚类结果也存在重大影响。

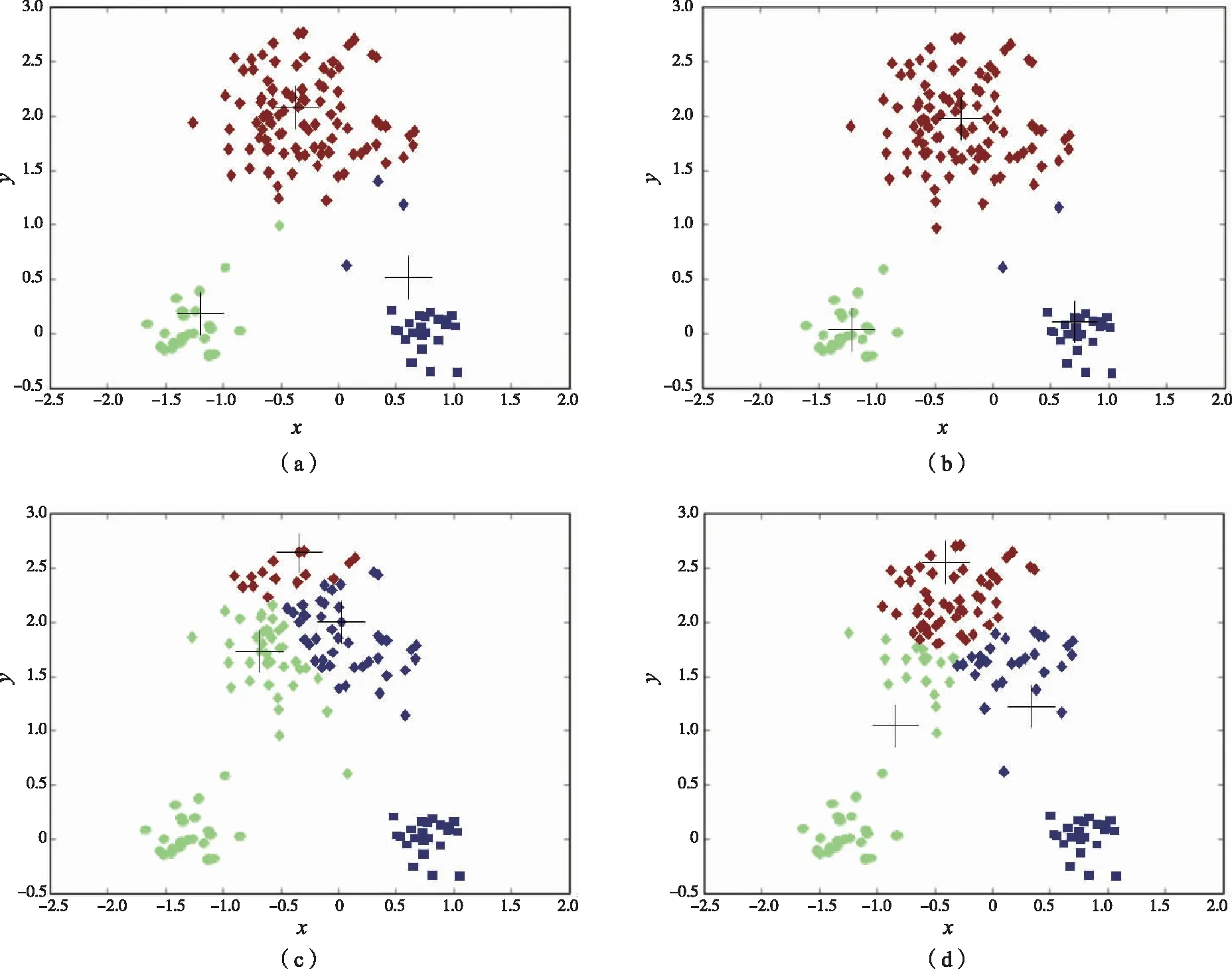
图1 初始簇中心对K均值聚类结果的影响Fig.1 The influence of initial cluster center on K-means clustering

试验数据中存在的异常数据会干扰聚类中心的计算，进而影响聚类结果。

3) 随机选择的K值对聚类结果影响较大。不同的初始值K可能导致数据点被分配到不同的簇中，从而导致结果非确定。

2 异常试验数据筛查方法

2.1 改进K均值聚类算法

为了解决初始簇中心的随机性问题，应遵循以下原则选择初始簇中心：避免选择异常数据点；在高密度且均匀分布区域内进行选择。

改进K均值聚类算法的流程如图 2所示。为选取合格的初始簇中心，执行以下步骤：①计算数据集中所有数据点的紧密程度，剔除较为稀疏的数据区域；②根据紧密程度，在数据密集区选择数据点作为第1个初始簇中心；③在该区域内选择与第1个初始簇中心距离最远的数据点作为第2个初始簇中心；④以此类推，后续初始簇中心均选择与已选簇中心距离最远者，以保证各个簇中心分布均匀。

例如，对于Rd空间上的数据集合X={x1,…,xi,…,xn}中的任一数据点xi，首先求其紧密度值为

T(xi)=1/∑xj∈GD(xi,xj)

(1)

式中：G为xi的m个最近邻数据点集合；D(xi,xj)为数据点xi与xj之间的距离。从数据集合X中剔除紧密度值小于∑xi∈XT(xi)/n的数据点，得到数据密集区集合X′。在X′中，取紧密度值最大者作为第1个初始聚类中心c1；取距离c1最远的数据点作为第2个初始聚类中心c2；第m(m∈[3,K])个初始聚类中心cm所对应的xi满足条件

(2)

改进K均值聚类算法可以有效避免选择异常的离群点作为初始簇中心，从而保证算法的迭代初始起点不会大范围地偏离真实的聚类中心。同时，以数据的紧密程度作为初始簇中心的选择依据，更加符合最优聚类中心选择方法。

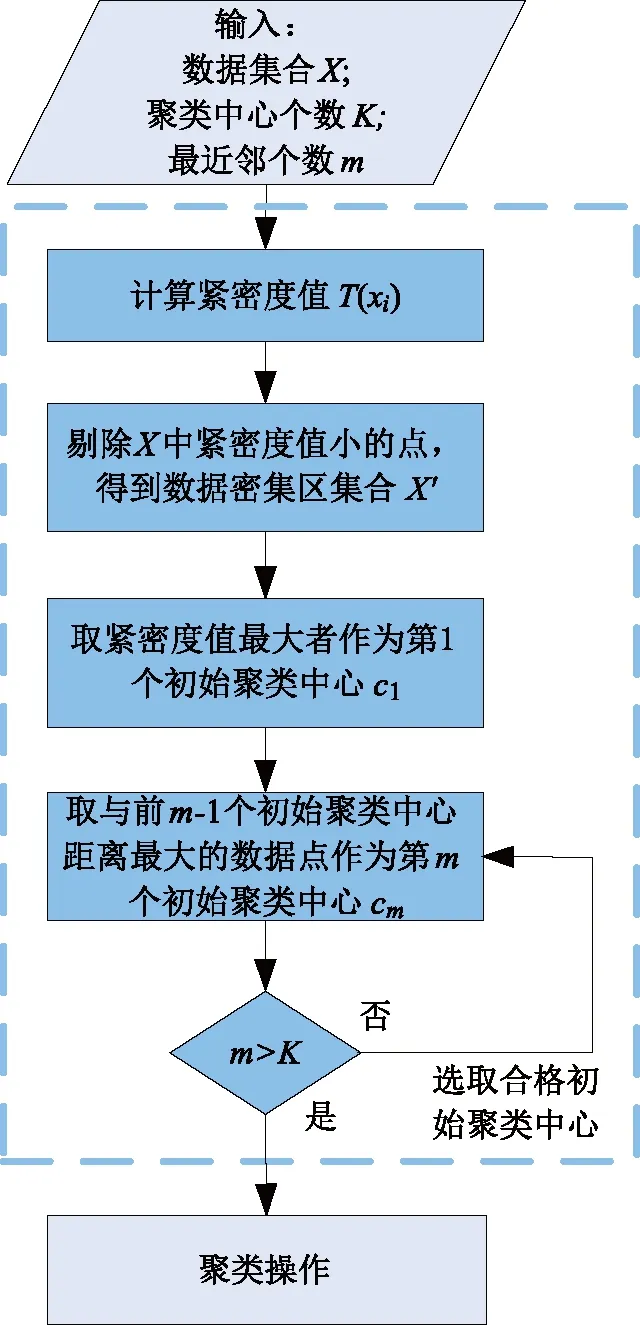
图2 初始聚类中心选择算法流程Fig.2 Flow chart of initial cluster center selected algorithm

2.2 异常试验数据筛查算法

根据K均值聚类算法特性，若在迭代过程中有离群点参与聚类中心计算过程，就会对聚类结果造成偏差。因此，基于对离群点敏感的特性，在改进K均值聚类算法基础上，提出异常试验数据筛查算法，利用迭代过程筛查并剔除异常试验数据点，算法流程如图3所示。

算法输入：Rd空间上的数据集合X={x1,…,xi,…,xn}；聚类中心个数K；聚类收敛阈值ε；最近邻个数m。

算法输出：聚类后的数据集C={c1,…,cj,…,cK}；数据xi的聚类标签L(xi)，异常数据点集合U。

初始化聚类准则函数J0=0，数据xi的异常度值A(xi)=0，根据初始聚类中心选择算法求得的K个初始聚类中心，分别对应K个聚类ωj(j=1,…,K)。计算X中所有数据点与各个聚类中心之间的距离，距离测度选择欧氏距离，则有

(3)

式中：i=1,…,n；j=1,…,K；k为聚类ωj中聚类中心数据点的标记。对数据点x，若有cj满足D(x,cj)=Dmin(x,cj)，则将数据点x归入cj所对应的聚类，即L(x)=ωj。在K个聚类中，若属于该聚类的数据点x与聚类中心的距离大于平均距离，即

D(x,cj)>(1/pj)∑L(x)=ωjD(x,cj)

(4)

式中：pj为cj的数据点总数，则记A(x)+ +。计算聚类准则函数为

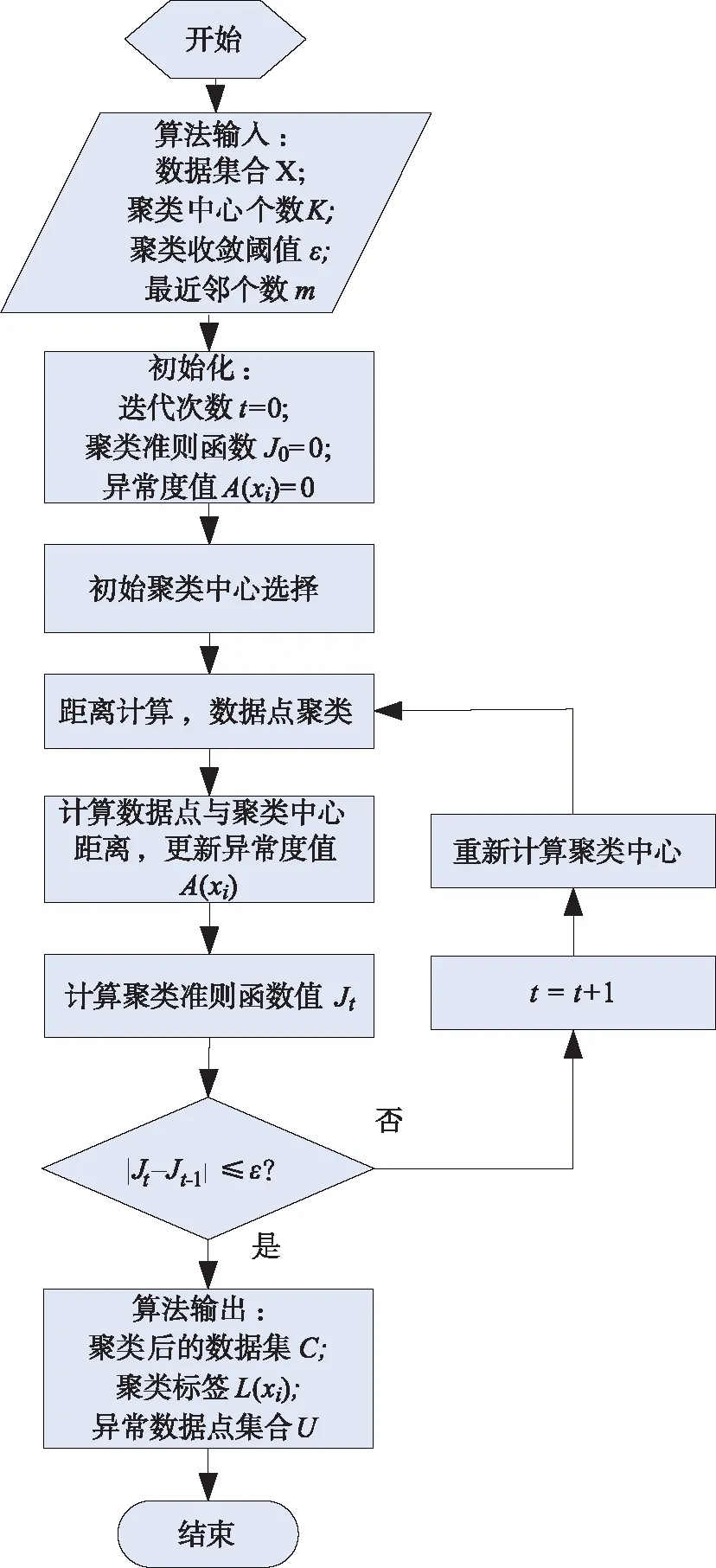
图3 异常试验数据筛查算法流程Fig.3 Flow chart of abnormal test data screening algorithm

(5)

若满足|Jt-Jt-1|≤ε，对所有数据的异常度值A(xi)求取平均值，将A(x)值大于平均值的数据点加入异常数据点集合U，算法结束；否则，根据各聚类的数据值，重新计算聚类中心，然后根据式(6)继续迭代。

cj(t)=(1/pj)∑L(x)=ωjx

(6)

上述算法基于改进K均值聚类算法，利用数据点与聚类中心的距离进行异常数据筛查判断。准确选择聚类中心是具备良好的异常数据筛查性能的基础。通过优化初始聚类中心的选择，选取距离真实聚类中心更近的数据点作为算法迭代起点，不仅可以提高聚类质量，而且可以提高异常数据筛查率。

3 实例验证

3.1 振动及应力筛选试验数据分析

以振动及应力筛选试验数据为例，选取其中-5 V无线电、引信输出两个通道数据对异常试验数据进行筛查。单个通道的试验数据分别如图4所示，采样点均为175 000个。其中，异常试验数据出现于图4(a)和(b)中红色圆圈处。

根据改进K均值聚类算法，对试验数据进行聚类，结果如图 5所示。为便于观察，选取-5 V无线电与引信输出两个变量，图5(a)为两个变量的三维显示结果，图5(b)为聚类中心个数K=2时的聚类结果，聚类中心用红色圆点标出。聚类结果与图4所示相一致，根据聚类结果，判断远离聚类中心的数据点为异常数据点。图5(b)中用虚线框标出了由聚类结果判断出的异常数据点，对应的-5 V无线电值为-4.95 V，这与图4(a)中的异常数据点也相一致；对应的引信输出值为4.50 V，这与图4 (b)中的异常数据点也相一致。

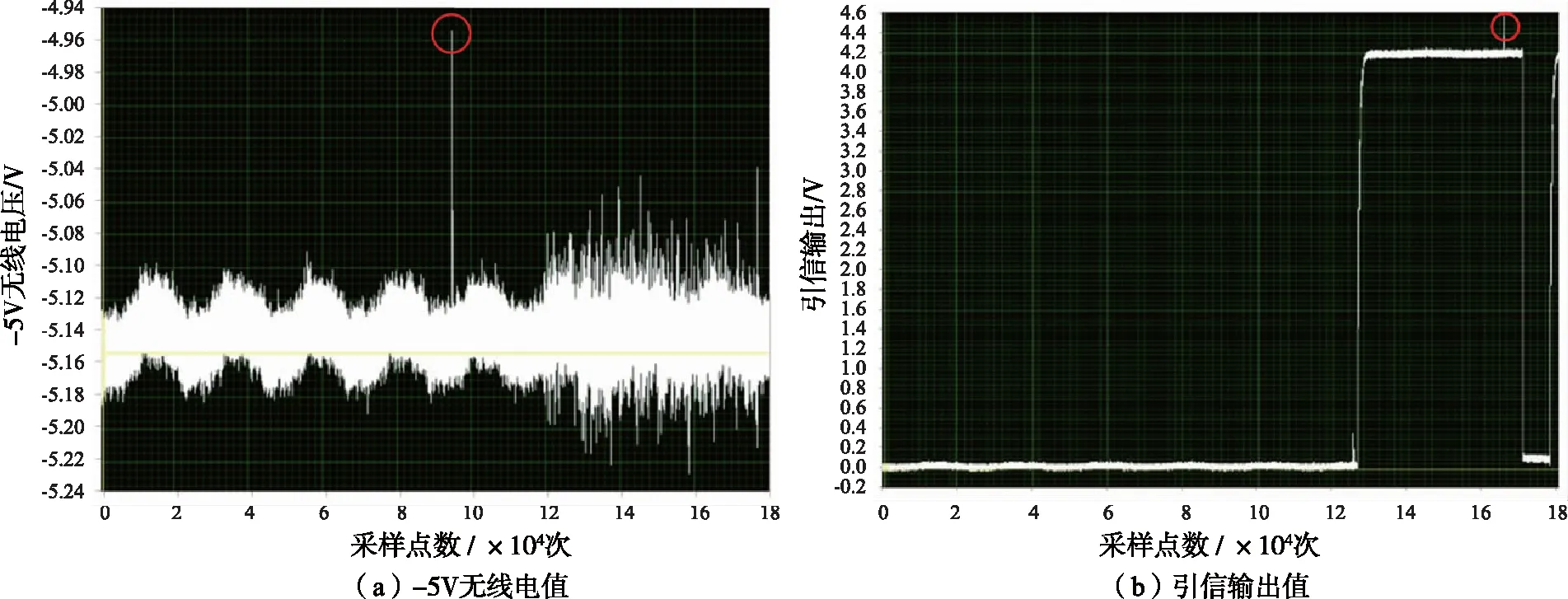
图4 振动及应力筛选试验数据Fig.4 Data of vibration and stress screening tests

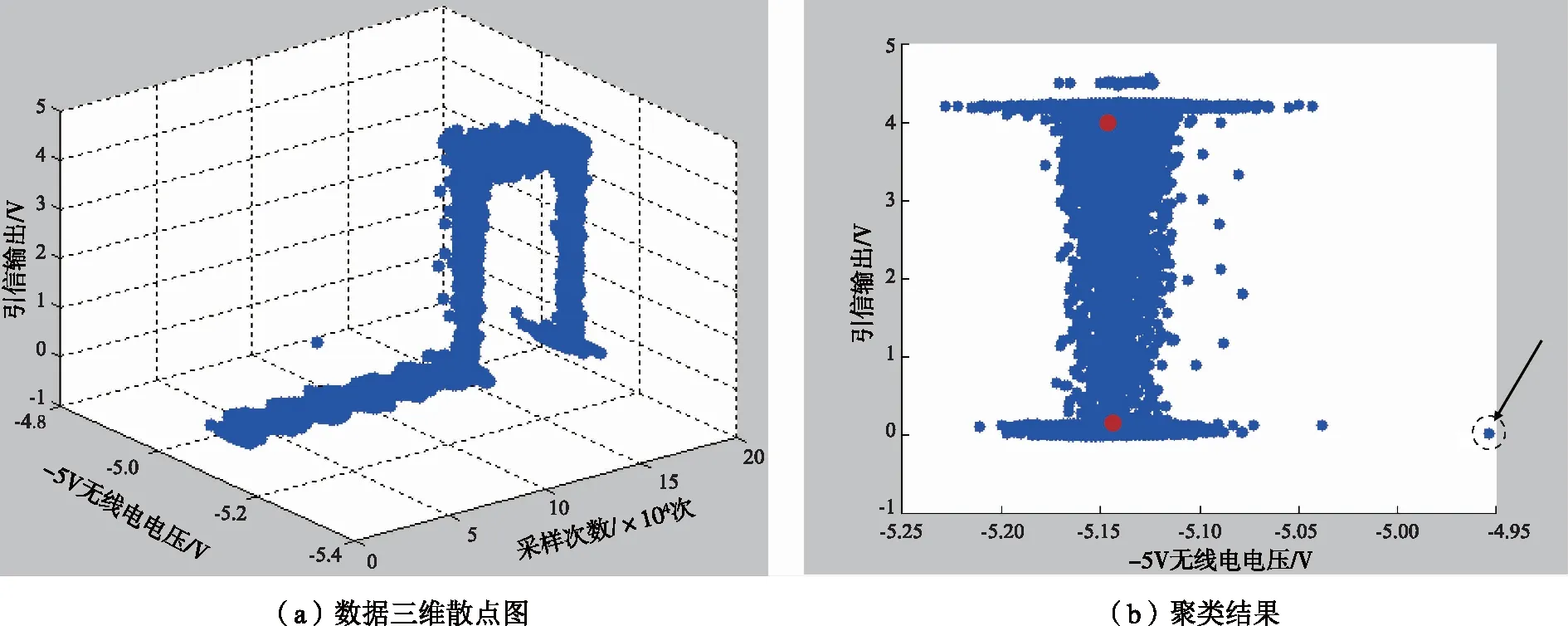
图5 -5 V无线电-引信输出三维显示和聚类结果Fig.5 3D plot and clustering result of -5V radio and fuze

3.2 算法性能比较

为了比较改进K均值聚类算法与基本K均值聚类算法的性能，在试验数据中随机加入10%的异常数据(在原始175 000个采样点中，随机叠加17 500个噪声点)，聚类中心个数K取2，分别进行10组实验，统计两种算法的检测率、误检率、迭代次数以及算法运行耗时等指标数据，实验结果如表1所示。

从表1可以看出，基本K均值聚类算法进行10次实验的平均检测率为74.8%，平均误检率为15.6%，迭代次数约为19次，平均耗时为95 s，且10次实验的检测率和误检率波动较大。改进K均值聚类算法进行10次实验的检测率、误检率、迭代次数以及耗时的均值都优于基本K均值聚类，分别为84.3%、9.4%、10次、62 s，且检测率和误检率波动较小。

因此，与基本K均值聚类算法相比，改进K均值聚类算法无论在检测率还是误检率方面都得到了优化，而且算法平均耗时较少，效率得到提升，同时指标数据的波动较小，算法运行更加稳定。

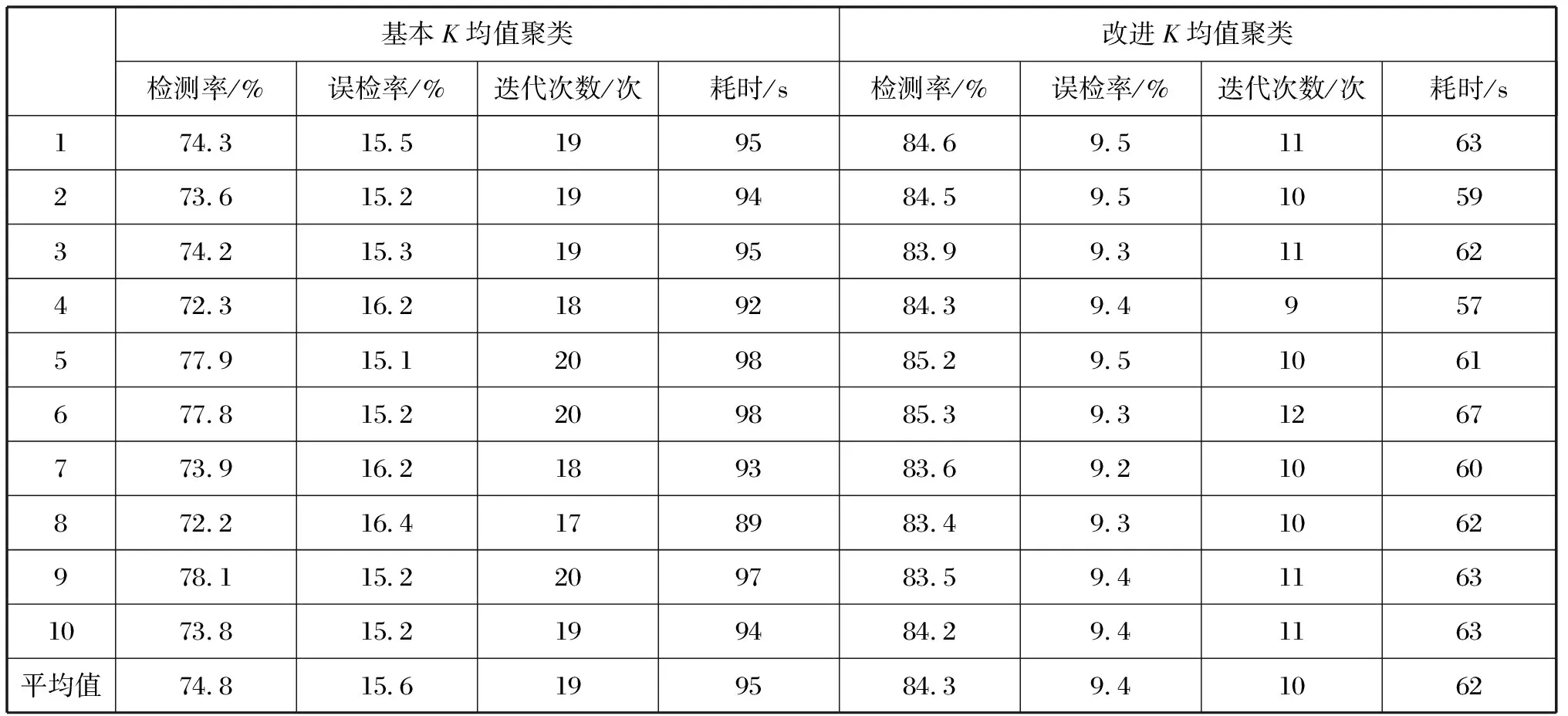
表1 聚类算法性能比较Tab.1 Comparison of clustering algorithm performance

4 结束语

针对战术导弹试验数据分析问题，本文引入数据挖掘技术，在分析K均值聚类算法局限性的基础上，提出了基于改进K均值聚类的异常试验数据筛查算法。通过选取距离真实聚类中心更近的数据点作为算法迭代起点，优化初始聚类中心的选择，以数据点与聚类中心的距离作为异常数据筛查判断的依据。将导弹振动及应力筛选试验数据作为算例进行分析，结果表明，与基本K均值聚类算法相比，本文提出的改进K均值聚类的异常试验数据筛查算法在聚类准确性和运行性能方面都有较大的提升。