浅谈中考数学动态问题
2019-11-25李峰
李 峰
(山东省禹城市伦镇中学 251200)
教学目标1.让学生理解动态问题中动点的变化过程,有拐点的或者动点速度发生变化的情况,认清变化过程的不同阶段.
2.找到动态问题中的不变的量,以静制动,把动态问题转化成静态问题来解决.
3.通过对动态问题的学习,进一步理解分类讨论,数形结合,化归转化的数学思想.
学考要求:中考常见题型,在中考中占重要位置.近几年中考几乎每年都考,动点问题有点动,线动,面动,难度依次增大,题目以选择填空居多,属中档题,解答题有时跟相似相结合属中高档题.
动(变化量):一般来说动点的时间,路程在运动过程中是不断变化的;
静(不变量):一般来说动点的速度,方向(折点,折线,分段)在运动过程中是不发生变化的.
关键:找临界点 临界位置,把运动过程分解.
宗旨:先定性结合选项排除,再定量依据关系式解答.
技巧:一般来说单个动点或单变量变化时图象是直线,双动点或者双变量变化时是曲线,增大的“”可以称之为上凸,增加得越来越慢,“”可以称之为下凸,增加得越来越快;减小的“”减小得越来越慢,“”减小得越来越快.

1.(四川资阳)如图1,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( ).
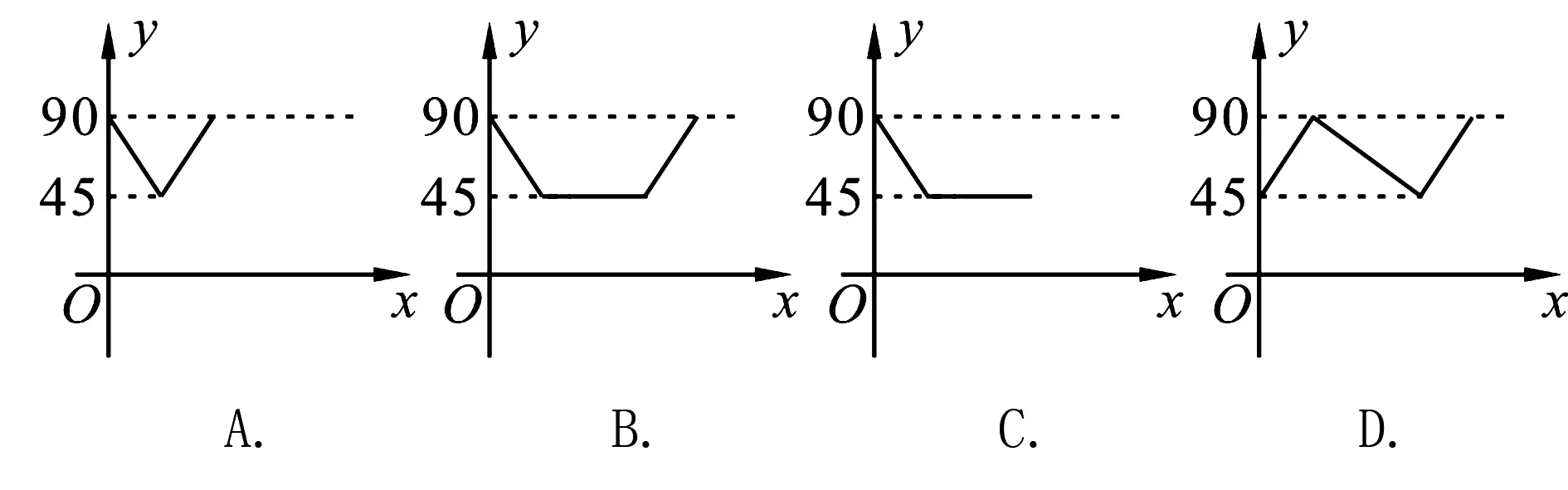
解析点P从点O出发,沿O→C→D→O运动过程中经过点C和点D时P的运动方向发生变化,图形应该是有两个折点,O→C时∠APB逐渐变小,对应图象逐渐降低;C→D时∠APB是弧AB所对圆周角不变,对应图象平行x轴;D→O时∠APB逐渐增大,对应图象逐渐升高.结合选项应该选B.
本题只要找到折点理解∠APB的变化情况,结合选项即可得到答案.

2.如图2,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( ).



3.如图3,点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( ).
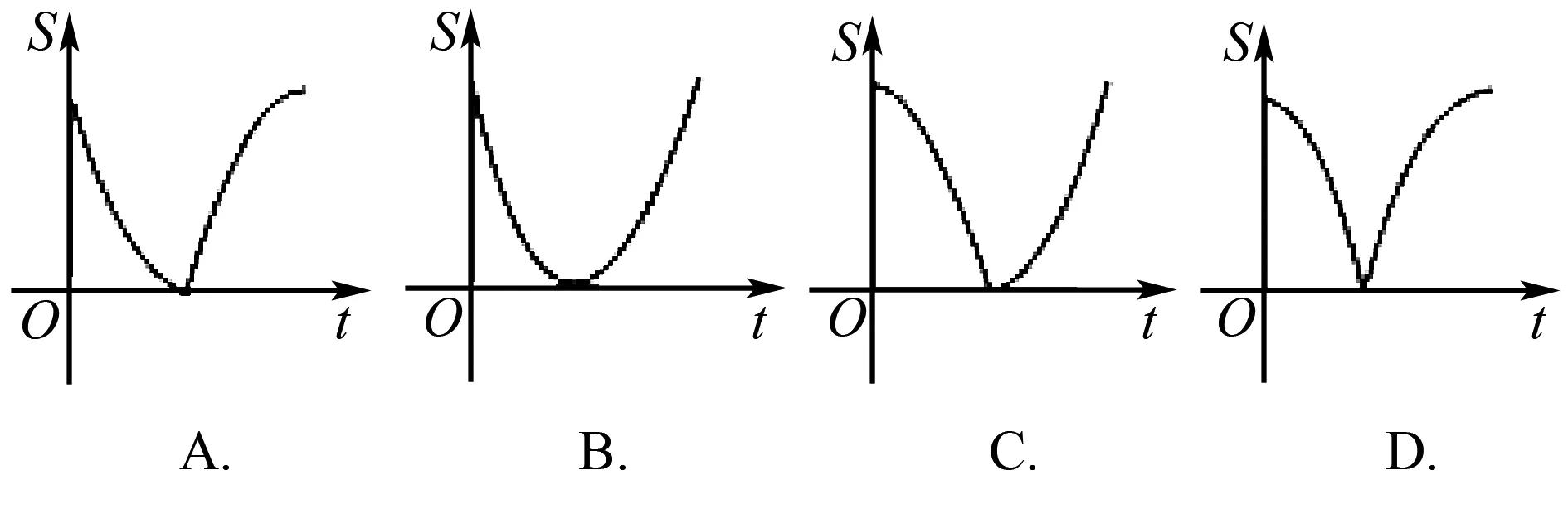
解析P从A→B过程中BP逐渐变短,S=πBP2面积变小,P从B→A过程中BP增大,面积S变大.面积S的图象具有轴对称性,B、D选项符合.又注意到P运动到AB中点时,圆的面积是圆最大面积的四分之一.观察选项B、D中的图象,只有B的图象符合.故选B.

4.如图4,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( ).


解析本题是双动点问题.可以先定性分析过D作DF⊥AB,易得AF=3,BF=CD=2.P从M运动到E需要7秒,Q从N运动到E需要5秒,所以时间t≤5.点Q有D,C两个折点,运动到D需要2秒,到C需要4秒,P有一个折点,运动到B需要4秒,图象应该在2秒,4秒,5秒的时候发生变化.2秒以前△APQ的底和高都增大,面积变化得快,图象应该是下凸,结合选项答案在C,D中.t=2时Q运动到D,AP=3,S=6;t=5时,如图5,S=1/2×PE×AB=5<6.选择D.
详细解答:略.(参考2016济南中考)

5.如图6,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( ).
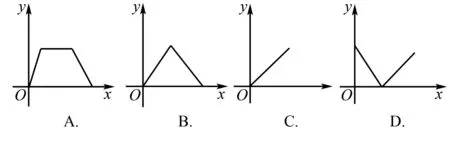
解析本题是线的移动问题.EF随着时间变化先增大后减小,A是折点,A点时最大.结合选项选B.
练习1.如图7,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图8是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是( )



A.A→B→E→GB.A→E→D→C
C.A→E→B→FD.A→B→D→C