高考动量守恒“高频模型”分析与归纳
2019-11-19
广西
(作者单位:广西区北海市合浦廉州中学)
动量守恒“高频模型”命题特点分析与归纳
“高频模型”为历年高考试题中出现频率比较高的模型,大多是高中物理主干知识。动量守恒定律是物理学中最基本的普适原理之一,也是高中物理教学的重要内容,同时还是高考考查的重点和热点,在历年高考中出现的频率很高,尤其是几种典型的“高频模型”。这些模型多立足于现实生活的实际问题,考查学生物理核心素养及综合分析能力。笔者通过研究历年高考试题,总结几种模型,并归纳解决此类题型一些方法,以飨读者。
一、人船模型
人船模型是一种反冲现象,即由人和船两个物体构成的系统,在该系统中,人和船在相互作用下各自运动,只有人与船的摩擦力,即摩擦力是内力,水面对船的阻力可以忽略不计,运动过程中该系统所受到的合外力为零,即人和船组成的系统在运动过程中总动量守恒。这类问题相互作用过程中系统的动能增大,有其他能向动能转化。可以把这类问题统称为反冲。
【例1】如图1所示,质量为m的人站在质量为M长为L静止小船的右端,小船的左端靠在岸边。当他向左走到船的左端时,船左端离岸多远?

图1

【点评】此结论与人在船上行走的速度大小无关,不论是匀速行走还是变速行走,甚至往返行走,只要人最终到达船的左端,那么结论都是相同的,人船模型问题是我们常遇到问题之一,本题所用方法和结果有普遍意义,但应注意l1、l2必须是相对同一参考系。
【扩展1】如图2所示,一个倾角为α的直角斜面体静置于光滑水平面上,斜面体质量为m,顶端高度为h,现有一质量为M的物体(M>m,且物体可以看做质点),沿光滑斜面下滑,当物体从斜面顶端自由下滑到底端时,斜面体在水平面上移动的距离是
( )

图2

【分析】由于斜面体放在光滑地面上,则物体下滑的过程中,斜面后退,由平均动量守恒可列式求解,列式时要抓住两物体运动的水平位移之和等于斜面的水平长度。

【点评】本题考查平均动量守恒定律的应用,要注意根据动量守恒得出两物体质量与水平长度的乘积也是守恒的。
二、滑块模型
滑块模型是指物块在木板上运动的情景,是一种物体相对运动的现象,由于两物体之间有相互作用力,会出现相对滑动的物理情景。一般来说,滑块受到木板的摩擦力约束,只能在一个平面上运动,无论相对静止还是相对滑动,都要分析两个物体之间的相互作用力。在高考中出现的题型各种各样,主要以受力分析为突破口进行考查,涉及动量守恒、牛顿运动定律、能量守恒等内容。
【例2】如图3所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,m 图3 (1)A、B最后的速度大小和方向; (2)从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动的位移大小。 【点评】本题关键是分析清楚两物体的运动过程,此类问题内部滑动摩擦力做功发热,能量守恒是我们常用方法Q=fs相对=Ek末-Ek初。 图4 (1)滑块C与A,B间的动摩擦因数及滑块C滑行的时间; (2)若解除锁定,再让滑块C以同样的初速度滑上长木板A。则最终A、B的速度分别为多少? 【分析】A、B两个长木板锁定在光滑水平面上时,滑块C从长木板A的左端进入刚好能停在长木板B的右端时速度为零,由功能关系求动摩擦因数μ,利用动量定理求运动时间。若解除锁定,三个物体组成的系统动量守恒。最终C停在B上,且两者速度相等,根据动量守恒定律和能量守恒定律结合求解。 【点评】本题综合运用了动量守恒定律、动量定理和能量守恒定律,关键要正确选择研究对象和研究过程,把握隐含的临界情况和临界条件,以及知道摩擦产生的热量Q=fΔs=fL相对。 动量守恒定律是矢量式,研究的很多系统中,在某一方向上,系统符合动量守恒定律的条件,那么,在这一方向上则可以利用动量守恒定律列方程,计算复杂的运动过程。 【例3】如图5所示,AB为一光滑水平横杆,杆上套一质量为M的小圆环,环上系一长为L质量不计的细绳,绳的另一端拴一质量为m的小球,现将绳拉直,与AB平行,由静止释放该小球,则当细绳与AB成θ角时,圆环移动的距离是多少? 图5 【点评】本题是以某一方向动量守恒为特点,以动量守恒定律等知识为依托,考查动量守恒条件的理解与灵活运用能力。 【扩展3】如图6所示,水平光滑轨道宽和弹簧自然长度均为d,m2的左边有一固定挡板,已知m1≥m2,m1由图示位置静止释放,当m1与m2相距最近时m1速度为v1,则求在以后的运动过程中( ) 图6 A.m1的最小速度是0 C.m2的最大速度是v1 爆炸类的模型,主要考查的是研究系统某一瞬间出现爆炸的情景。在爆炸的过程中,内力远大于外力,则系统可以近似处理为动量守恒。爆炸模型类似反冲特点,这类问题相互作用过程中系统的动能增大,有其他能向动能转化。 【例4】抛出的手雷在最高点时水平速度为10 m/s,这时突然炸成两块,其中大块质量300 g仍按原方向飞行,其速度测得为50 m/s,另一小块质量为200 g,求它的速度的大小和方向。 【分析】手雷在空中爆炸时所受合外力应是它受到的重力G=(m1+m2)g,可见系统的动量并不守恒。但在爆炸瞬间,内力远大于外力时,外力可以不计,系统的动量近似守恒。 【点评】爆炸类的题型类似于反冲,都是由其他形式的能转化为动能。 子弹打木块实际上是一种完全非弹性碰撞。作为一个典型模型,它的特点是子弹以水平速度射向原来静止的木块,并留在木块中与木块共同运动,下面从动量、能量和牛顿运动定律等多个角度来分析这一过程。 【例5】设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹平均阻力的大小和该过程中木块前进的距离。 图7 【点评】这个式子的物理意义为f·d恰好等于系统动能的损失;根据能量守恒定律,系统动能的损失应该等于系统内能的增加;可见f·d=Q,即两物体由于相对运动而摩擦产生的热(机械能转化为内能)等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热与路径有关,所以这里应该用路程,而不是用位移)。做这类题目时一定要画好示意图,把各种数量关系和速度符号标在图上,以免列方程时代错数据。 图8 【点评】对于复杂的物理问题要搞清物理过程,要明确是否满足动量或机械能的守恒条件,特别是碰后的两物体有共同速度的情况,机械能损失最大,所以动量守恒时,机械能不一定守恒。 【例6】甲乙两球在水平光滑轨道上同方向运动,已知它们的动量分别为P甲=5 kg·m/s,P乙=7 kg·m/s,甲从后面追上乙并发生碰撞,碰撞后乙球动量变为10 kg·m/s,则两球质量m甲与m乙间关系为 ( ) A.m甲=m乙B.2m甲=m乙 C.4m甲=m乙D.6m甲=m乙 【点评】碰撞的特点为①作用时间极短,内力远大于外力,总动量总是守恒的;②碰撞过程中,总动能不增加,因为没有其他形式的能量转化为动能;③碰撞过程,两物体产生的位移可忽略。 【扩展3】静止在水平地面上的两小物块A、B,质量分别为mA=1.0 kg,mB=4.0 kg;两者之间有一被压缩的微型弹簧,A与其右侧的竖直墙壁距离l=1.0 m,如图9所示。某时刻,将压缩的微型弹簧释放,使A、B瞬间分离,两物块获得的动能之和为Ek=10.0 J。释放后,A沿着与墙壁垂直的方向向右运动。A、B与地面之间的动摩擦因数均为μ=0.20,重力加速度取g=10 m/s2。A、B运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短。 图9 (1)求弹簧释放后瞬间A、B速度的大小; (2)物块A、B中的哪一个先停止?该物块刚停止时A与B之间的距离是多少? (3)A和B都停止后,A与B之间的距离是多少? 对于高考压轴题来说,运动的多重性、研究对象的复杂性是解决问题的关键。三体两次作用的问题,主要是多过程交织在一起,试题具有一定的难度。 【例7】如图10所示,长木板A静止放在水平地面上,其右端叠放着物块B,左端恰好在O点,水平地面以O点为界,左侧光滑,右侧粗糙。物块C(可以看作质点)和物块D之间夹着一根被压缩的弹簧,并用细线锁住,此时弹簧的弹性势能为8 J,两者以共同的速度v0=6 m/s向右运动,某时刻细线突然断开,物块C与弹簧分离后,撤去物块D,物块C与长木板A碰撞并与之粘连(碰撞时间极短)。已知A、B、C、D的质量均为m=2 kg,木板A的长度l=6 m,A、C与粗糙地面间的动摩擦因数相同,均为μ1=0.1,A、B间的动摩擦因数为μ2=0.2,最大静摩擦力等于滑动摩擦力,重力加速度为g=10 m/s2。 图10 (1)求物块C和弹簧分离时物块D的速度大小; (2)求最终物块B离长木板A左端的距离; (3)若物块C与长木板A碰撞的同时,在长木板A的右端施加一水平向右的恒力为F=18 N,经过一段时间后撤去,物块B刚好不从长木板的左端滑出,求恒力F作用的时间。 图11 【点评】本题的问题比较复杂,过程也比较多,对于复杂的物理问题要搞清物理过程,要明确是否满足动量或机械能的守恒条件,特别是碰后的两物体有共同速度的情况,机械能损失最大,所以动量守恒时,机械能不一定守恒,这时应注意用动能定理或者功能关系进行求解。





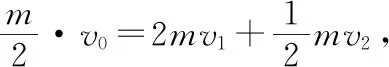
三、某一方向上的动量守恒

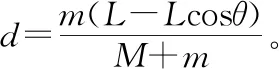




四、爆炸类问题

五、子弹打木块模型
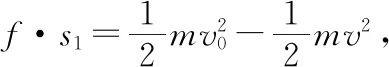


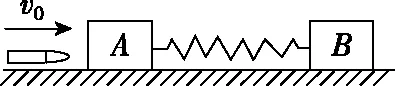
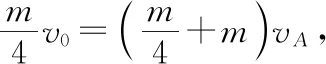

六、碰撞模型




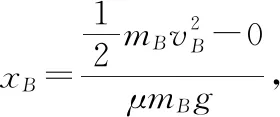

七、三体两次作用模型(能量和动量综合问题)






