物理模型在解题中的应用

福建

(作者单位：福建省漳州市漳浦第一中学)

利用物理模型分析解题，能使复杂的题目大大简化

高中物理涉及的范围广，内容多，题型复杂，要解决这些问题需要利用抽象的解题思维能力，故而学生普遍感到物理难学，题目难解，对物理产生畏难情绪。在新高考模式下，一些先试先行的省份，采取3+3模式后，出现了物理遭到大面积弃选的现象。这与我国现阶段大力发展自主创新产业，需要大量科技人才的背景不相适应。而这些没选物理的学生，进入大学后，对有些专业的学习也出现了困难，致使有些高校还要给学生补上高中物理课，造成很多麻烦。现在一些省份开始实行3+1+2高考选科模式，依然有相当多学生不敢选物理。在这种背景下，如何让学生更好地学习物理知识，更得心应手地解决物理问题，使学生对物理学科不再惧怕，显得十分重要。尤其高三阶段，学生已经学习了高中的全部物理知识，面对高考总复习中的茫茫题海，常常无所适从。因此，如何教会学生采用适当的方法，理解和解答各种题型，是老师们应当思考的问题。

面对一道题，学生首先要对题目进行分析，分析题目的已知条件，物理情景，满足什么物理规律，应采用何种定律、公式解题。题目纷繁复杂，题型多种多样，如何选择正确的物理方法解题，有很大难度。但物理试题有很多共性，可抽象出同样的物理模型，从而应用相似的方法解题。这样，学生只要掌握了多种物理模型，便能得心应手地应用解题。下面以几种物理模型为例，让学生领会应用物理模型解题的方便性和实用性。

一、用一种模型解释科技领域中的不同实例，帮助学生理解掌握各种情况

例如学生刚接触到磁流体发电机、电磁流量计和霍尔效应等实例时，往往感到复杂多样。上课看似听懂了，可是当独立分析解题时，往往还会出现困难。若教师能够引导学生利用速度选择器模型，加以总结分析，就会让学生感到这些实例简洁易懂，从而轻松掌握它们的原理，不易混淆。分析如下：

1.速度选择器

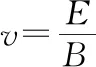
2.磁流体发电机

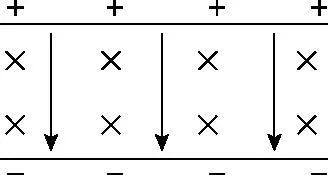
高温等离子体源源不断地射入如图2所示的平行极板AB间，带电粒子由于受到洛伦兹力的作用发生偏转，带正电粒子积累在下极板，带负电粒子积累在上极板，从而产生了电场，形成如图3所示复合场(磁场方向为N极指向S极)。当射入的粒子受到的电场力小于洛伦兹力时，粒子继续偏转，电场强度继续增强，直到当后续的粒子再射入板间受力平衡时，粒子不再偏转，达到动态平衡状态，此时构建的复合场与图1中右图所示的速度选择器相似，也可以看成速度选择器模型，粒子受到的电场力和洛伦兹力平衡，即qBv=qE，再根据U=Ed，得U=Bdv。这样两极板间形成电势差，即成为一个可对外供电的电源，这就是磁流体发电机原理。

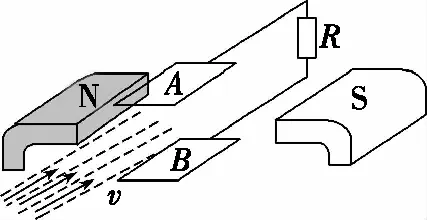
图2

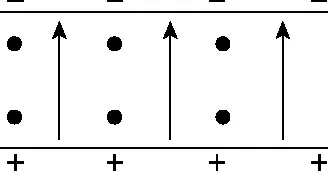
图3

3.电磁流量计

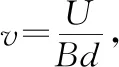
图4

图5

4.霍尔效应

图6

二、物理模型对实际生活中实例的解释

生活中处处有物理知识。近年来，让学生对生活中的现象应用物理规律分析，也是高考的热点。

1.日常生活中实例解释

例如力的分解对拉链为何易拉、斧头有效劈柴的解释。

力是矢量，它的分解满足平行四边形定则，对它的分解有多种方法。其中，按力的效果分解是常用的方法。人们常见的拉链很容易被拉开，是由于拉头与拉链接触的地方是三角形，如图7所示，对拉头施加一个向下的拉力，对此力向垂直于三角形两边的方向进行分解，可以发现，两个分力比向下的拉力大得多，这样拉链很容易就被拉开了。同样的道理，斧头劈柴的原理，也可以这样来分析。

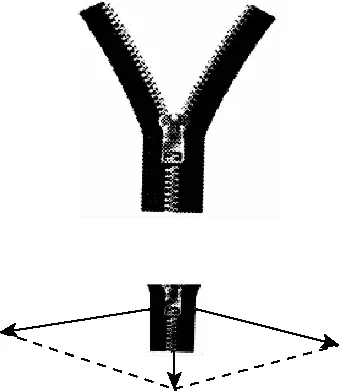
图7

2.体育运动中的物理知识

例如平抛模型对一些体育运动的解释。

平抛运动是高中物理的一个重点知识，也是高考的重点，几乎年年高考都会出现平抛或类平抛运动模型的考题。近年来，用平抛运动的规律来解释一些体育运动，成为出题者的喜爱。在近几年的高考中，就较为频繁地出现了这类题型。例如，2015年全国卷Ⅰ第18题中乒乓球发射机水平发射乒乓球的题目(如图8)；2015年浙江理综第17题，足球运动员沿水平方向顶足球攻门，足球做平抛运动，射入球门左下方死角的题目(如图9)；排球运动员水平击打排球，研究排球既不触网又不出界等排球的落点问题(如图10)；滑雪运动员经过倾斜向下的曲道加速后，沿水平滑道飞出，落在斜面上的问题(如图11)。此外，还有带电粒子在匀强电场中的类平抛问题等等，都是高考的热点。像这类的题型，都可以把物体的运动看成平抛运动，从而应用平抛运动规律来解题。学生只要分析出这种类平抛的运动模型，熟练掌握平抛运动的规律，列出相关方程，问题就能得到解决。

图8

图9

图10

图11

三、特殊物理模型在解题中的应用

一些物理模型结论有趣且实用，如果能掌握它们的规律，在解答相似题型时直接应用其二级结论，可以做到省时省力，同时提高解题准确性。

下面以等时圆模型为例，三根光滑细杆端点都在圆环上，如图12所示放置。物体分别沿三条路径的上端点无初速度释放，到达最低点的时间是相同的，这个等时圆的结论并不难推导。

图12

接下来，我们利用等时圆的规律来解决一些变式题。如图13所示，两根光滑杆AM和BM，紧靠在竖直放置的圆环上，与图12所示的等时圆不同的是，BM杆的B端高出了圆环与墙的接触点。现要求判断物体分别从B端和A端无初速释放，要到达M点，沿哪条路径更快。这道题显然可以看成等时圆的变形题，若物体从BM杆与圆的交点滑下，显然比从B点无初速下滑时间短，故而题中的两条路径显然是沿AM物体能更快到达底端。

图13

再看下一个变式题，如图14所示，此图只是变换成两个竖直叠加的相切圆，P为相切点。要判断物体由两条光滑的路径APB和CPD无初速度分别下滑，所用的时间关系只需按照等时圆原理的推导方式，即可推出两条路径时间相等的结论。显然，学生平时如果能够充分理解等时圆的特点，看到这类的题型，便能立即使用等时圆模型的等时性规律进行分析，从而可以快速得出正确答案。

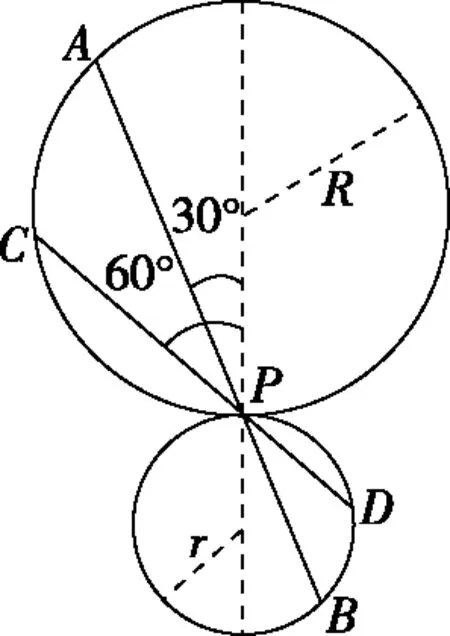
图14