知“三”求“二”确定磁场中轨迹圆的圆心
2019-11-19
湖北
(作者单位:湖北省利川市第五中学)
知“三”求“二”定圆心,精准高效真省心
带电粒子在磁场中运动是高考的热门考点,也是学生难以掌握的核心知识之一。磁场问题题型乱、方法杂、解答难,学生不易建立知识网络。笔者发现“知三求二”的方法可以有效地帮助学生归纳整理此类问题。
一、方法简介
1.磁场中纯轨迹问题,一般可以把重要信息归结为五个要素:
A.入射点 B.入射方向 C.出射点 D.出射方向
E.半径
2.对于一般磁场问题而言,只要知道其中任意三个要素就可以确定带电粒子在磁场中运动轨迹的圆心,当然也可以求出剩下的两个要素。故名知“三”求“二”,类似运动学中的知“三”求“二”(x、t、v0、vt、a)和等差数列中的知“三”求“二”(a1、公差d、n、an、Sn)。
①ABC、ACD、ACE:中垂线法
②ABE、CDE:直接法
③ABD、BCD:估计法
④BDE:角平分线法
⑤ADE、BCE:动圆法
二、基础例题
1.只要知道带电粒子某点速度方向,都可以过该点作其速度方向的垂线
【例1】如图1所示,质量为m,电荷量为q的带负电粒子,不计重力,与AB边成60°从M点进入匀强磁场。已知磁场垂直纸面向里,宽度为d,磁感应强度为B。

图1
(1)若粒子从N点射出磁场,且MN=d,求粒子的速度大小。
(3)若要让粒子从入射AB边射出磁场,求粒子入射速度的最大值。

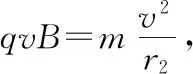
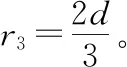
【感悟】1.三类题都要过入射点作入射速度方向的垂线,这样做的目的就是把圆心束缚在这条垂线上。2.中垂线法是连接入射点和出射点成弦并作弦的中垂线,则圆心必然在此垂线上,故交点即圆心。3.直接法是圆心到入射点(圆周上的点)必为半径。4.估计法作两速度方向的垂线,再通过一定点(圆周上的点)来确定另一圆周上的点,从而得到圆心。
【训练1】如图2所示,质量为m,电荷量为q的带正电粒子,垂直OA边从A点射入磁感应强度为B的有界匀强磁场。已知磁场垂直纸面向里,∠AOB=30°且OA=3d。

图2
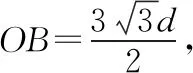
(3)若要粒子在OA边射出,求粒子速度的最大值。

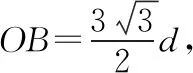
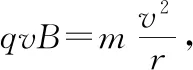
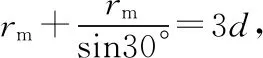
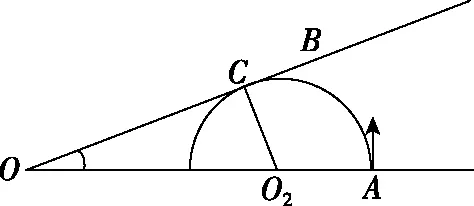
图3
2.知两速度方向却无定点时优先考虑角平分法
【例2】如图4,一带电质点,质量为m,电荷量为q,以平行于Ox轴的速度v从y轴上的a点射入图中第一象限所示的区域,为了使该质点能从x轴上的b点以垂直于Ox轴的速度v射出,可在适当的地方加一个垂直于xy平面、磁感应强度为B的匀强磁场,若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径,重力忽略不计。

图4
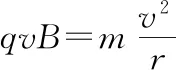
【感悟】1.遇速度方向就作其垂线,无定点时要想到用估计法。2.圆心可以被束缚在角平分线上。
【训练2】在如图5所示的平面直角坐标系xOy中,有一个圆形区域的匀强磁场(图中未画出),磁场的磁感应强度为B,方向垂直于xOy平面向里,O点为该圆形区域边界上的一点。现有一质量为m、带电荷量为+q的带电粒子(不计重力)从O点以初速度v0沿x轴正方向进入磁场,已知粒子经过y轴上P点时速度v方向与y轴正方向夹角为θ=30°,求OP之间的距离。
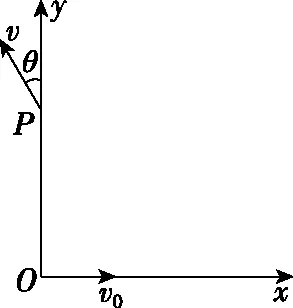
图5
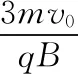
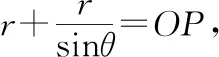

图6
3.入射方向任意时,多靠动圆法帮助
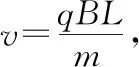
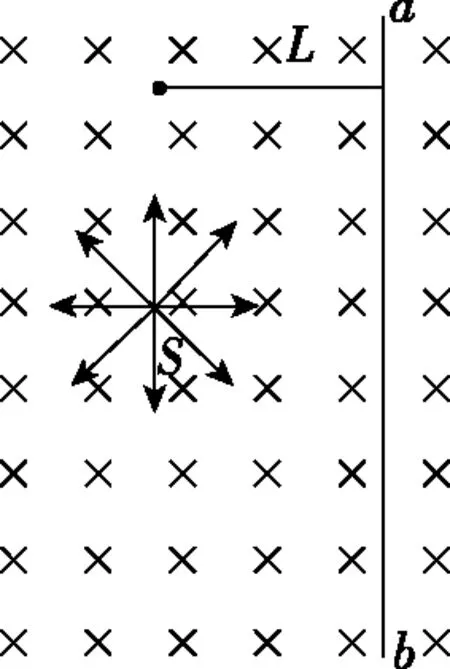
图7
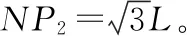
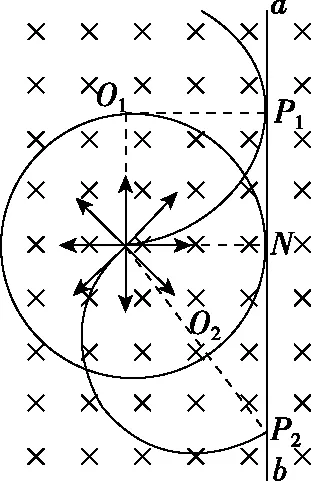
图8
【感悟】知道半径时,圆心可以被束缚在某个圆上。
【训练3】将例3中的ab板绕N点(图7中未画出,N点与S点处在同一水平线上)逆时针旋转30°,其余条件不变,求ab板上被α粒子打中的区域的长度。
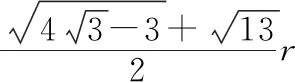
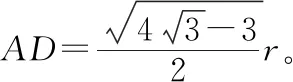
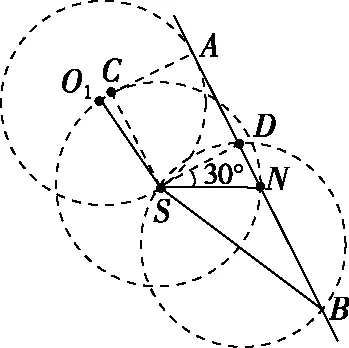
图9
三、强化训练
1.有些题目看似不属于这些类型,但其实只是某种类型的特例而已。
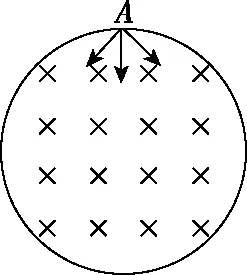
图10
【例4】如图10所示,半径为r的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B,磁场边界上A点有一粒子源,可以在纸面内源源不断地向各个方向发射速度大小均为2kBr的带正电的粒子(重力不计),其中k为粒子的比荷,则粒子在磁场中运动的最长时间为
( )
【答案】B


图11
【感悟】此题知入射点和半径,隐藏的另一个要素是出射点(因为出射点一定在圆上),要运动的最长时间则是圆心角越大,即对应的弦(入射点和出射点的构成的线段)越长,这样就把出射点锁定,属于中垂线法。

图12
【变式训练】如图12,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,P为磁场边界上的一点,大量相同的带电粒子以相同的速率经过P点,在纸面内沿不同方向射入磁场。若粒子射入速率为v1,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速率为v2,相应的出射点分布在三分之一圆周上。不计重力及带电粒子之间的相互作用。则v1∶v2为
( )
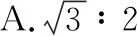
【答案】C

2.角平分线法的灵活运用

( )
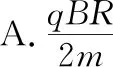

图13

图14
【答案】B

【感悟】本题的角平分线不好画,但知两速度方向时用角平分线方法较容易,故研究角平分线还可以与谁联系起来,发现在圆形磁场中角平分线一定会过磁场圆心。
三、小结
1.带电粒子在磁场中轨迹圆的圆心确定方法很多种,归根到底是想办法把圆心束缚住,如过点作速度方向的垂线就是把圆心束缚在垂线上,再作中垂线也是把圆心束缚在中垂线上,两线交点即为圆心。而圆心还可以被束缚在角平分线上以及某个圆上,有了这些认识后加以练习,就不会再感觉磁场问题又难又杂了。

