巧用“转元法”处理高中“非线性”变化物理问题

福建

(作者单位：福建省南平市南平九中)

山重水复疑无路，柳暗花明又一村

在不同的物理图象中，斜率是决定物理过程中每个阶段图象走势的关键信息。但某些情况下直接用纵横坐标变化量的比值，无法看出斜率代表的物理意义，此时可以通过“转元法”把已知的微元关系转换成未知的微元关系，对取得的微元进行转化，找出新的微元关系。本文从数学的思维方法对“转元法”进行铺垫，调研高中物理常见的几种微元并进行“转元”，使物理关系的研究方向明朗化，采取定性和半定量的方式分析物理问题，使得复杂问题迎刃而解，旨在培养学生的创新思维意识和提高应用数学解决物理问题能力。

一、应用“微元法”，数学思想通过“转元法”化归物理意义

二、巧用“转元法”，数形结合处理“非线性”变化物理问题

( )

A.若A不变，则a也不变

B.若A>0且保持不变，则a逐渐变大

【调研试题2】行驶中的汽车遇到红灯刹车后做匀减速直线运动直到停止，等到绿灯亮时又重新启动开始做匀加速直线运动直到恢复原来的速度继续匀速行驶，则从刹车到继续匀速行驶这段过程，位移随速度变化的关系图象描述正确的是

( )

A

B

C

D

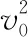
【调研意图】本题通过解图象题的常规思路与“转元法”进行对比：当图象走势未知时，要把图象对应的函数关系式推导出来，根据图象反映的函数关系，找到图象所反映的两个物理量间的关系，分析其物理意义和变化规律。而采用的“转元法”，只需考虑图象斜率的变化规律即可进行判断，抓住了解决图象问题的根本，殊途同归。

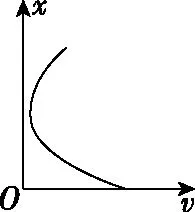
【调研试题3】一带正电的试探电荷，仅在电场力作用下沿x轴从x=-∞向x=+∞运动，其速度v随位置x变化的图象如图所示。x=x1和x=-x1处，图线切线的斜率绝对值相等且最大，则在x轴上

( )

A.x=x1和x=-x1两处，电场强度相同

B.x=x1和x=-x1两处，电场强度最大

C.x=0处电势最高

D.从x=x1运动到x=+∞过程中，电荷的电势能逐渐增大

【调研意图】本题在教辅资料上频频出现，无论是网上或教辅的参考答案上，基本都是类似如下解析：“速度随位置的变化率即斜率体现的是加速度的变化，根据F=ma及F=qE可知电场强度取决于加速度，也就是斜率，x=x1和x=-x1两处斜率最大，则电荷的电场强度最大”，这种错解错析流行较广，而该题的图象是速度-位置图象，速度-位置图象的斜率不等于加速度，也不表示加速度，根据“转元法”可以很清晰地推导出无从判断场强E的大小，此类问题要引起足够的重视。

【调研试题4】如图所示，MN和PQ是电阻不计的平行金属导轨，其间距为L，导轨弯曲部分光滑，平直部分粗糙，右端接一个阻值为R的定值电阻。平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场。质量为m、电阻也为R的金属棒从高为h处静止释放，到达磁场右边界处恰好停止。已知金属棒与平直部分导轨间的动摩擦因数为μ，金属棒与导轨间接触良好。则金属棒穿过磁场区域的过程中

( )

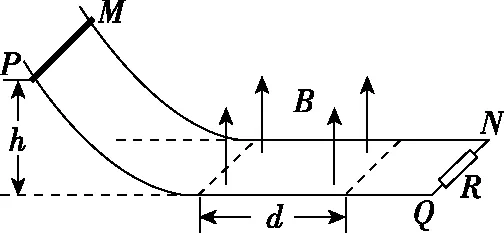
A.流过定值电阻的电流方向N→Q

【调研试题5】(改编)如图甲所示为一个质量为m、电荷量为+q的圆环，可在水平放置的足够长的粗糙细杆上滑动，细杆处于磁感应强度为B的匀强磁场中，不计空气阻力，现给圆环向右的初速度v0，在以后的运动过程中，圆环运动的动能Ek与时间t图象可能正确的是

( )

甲

A

B

C

D

【解题思路】(1)当qv0B=mg时，杆的弹力为0，摩擦力为0，圆环做匀速直线运动。Ek-t图象是一条平行于t轴的直线。

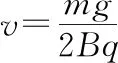
常规解法：由Wf=Ek-E0得Ek=E0+Wf=E0-Pft=E0-fvt=E0-μ(qvB-mg)vt，即斜率Ek-t图象的斜率k=-μ(qvB-mg)v。