“动能+势能”的守恒定律归类例析

重庆

(作者单位：重庆市第三十七中学校)

能量守恒，此消彼长

功能关系指的是“功是能量转化的量度”，力对物体做了多少功就有多少能量(该力对应的能)发生转化，如果扩大研究系统，虽然有力做功，但系统的总能量仍保持不变，只是系统内不同种类的能量发生了转化，即“此消彼长”。如：只有重力做正功，物体的重力势能减少，动能增加，且减少的重力势能等于增加的动能，但动能和重力势能的总和保持不变，机械能守恒。高中物理中这样的守恒形式还有很多，笔者总结了动能与势能相互转化但总量保持不变的系列守恒定律，如下表所示：

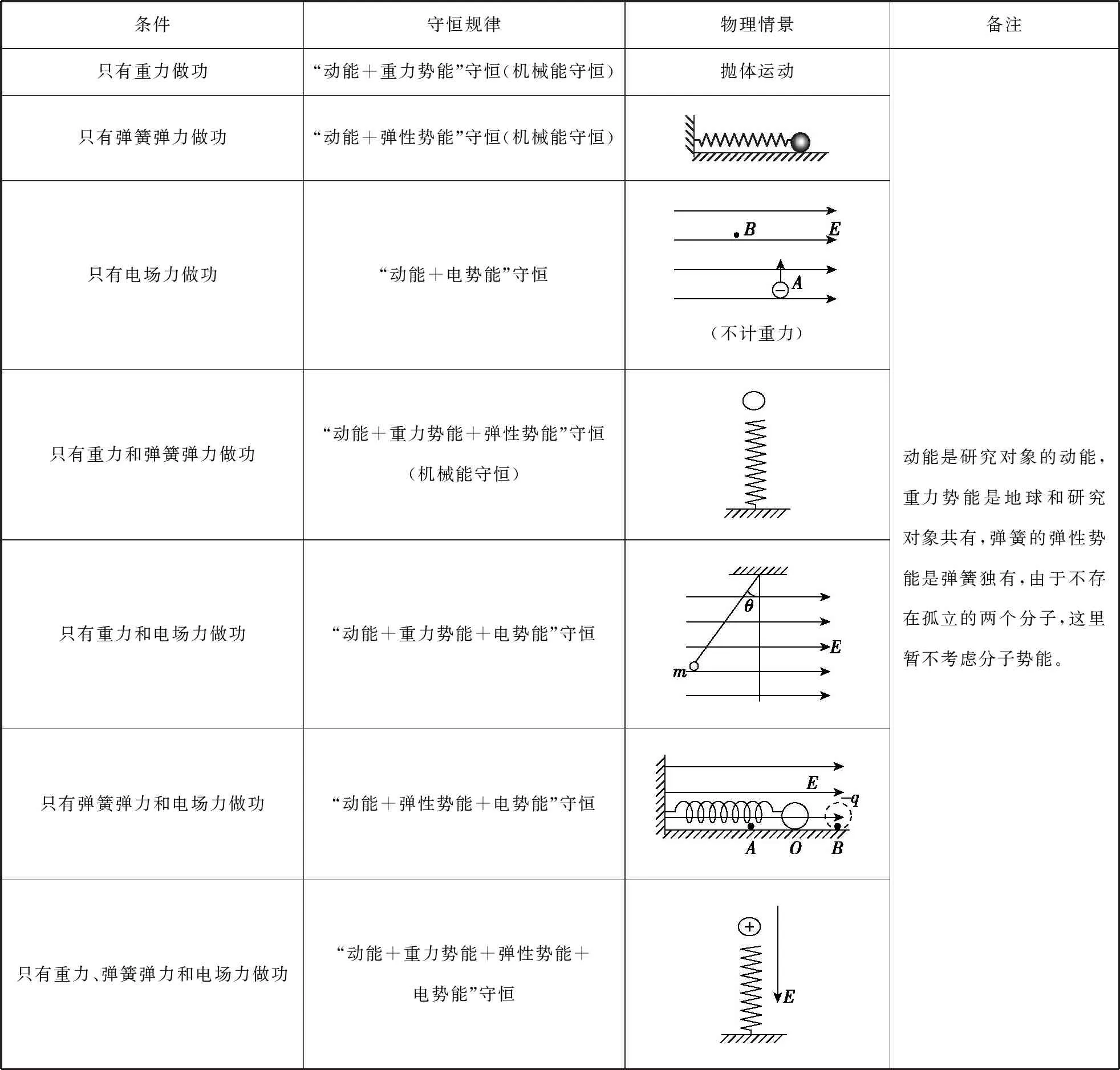
条件守恒规律物理情景备注只有重力做功“动能+重力势能”守恒(机械能守恒)抛体运动只有弹簧弹力做功“动能+弹性势能”守恒(机械能守恒)只有电场力做功“动能+电势能”守恒(不计重力)只有重力和弹簧弹力做功“动能+重力势能+弹性势能”守恒(机械能守恒)只有重力和电场力做功“动能+重力势能+电势能”守恒只有弹簧弹力和电场力做功“动能+弹性势能+电势能”守恒只有重力、弹簧弹力和电场力做功“动能+重力势能+弹性势能+电势能”守恒动能是研究对象的动能,重力势能是地球和研究对象共有,弹簧的弹性势能是弹簧独有,由于不存在孤立的两个分子,这里暂不考虑分子势能。

机械能守恒的情形比较普遍，在此不再赘述。

【例1】(“动能+电势能”守恒)在光滑水平面内有一沿x轴的静电场，其电势φ随坐标x的变化关系如图1所示，一质量为m，带电荷量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动，则下列叙述正确的是

( )

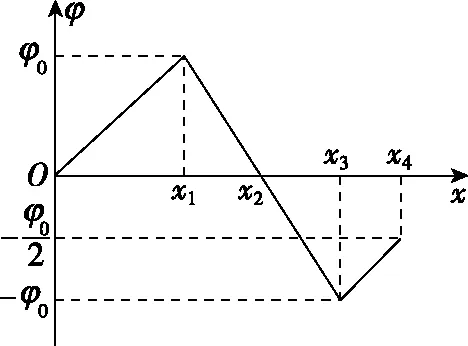
图1

A.若小球能运动到x1处，则该过程小球所受电场力逐渐增大

B.带电小球从x1运动到x3的过程中，电势能先减小后增大

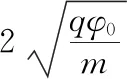
【答案】D

【点评】在静电场中，力学规律依然成立，只是在受力分析时多了一个电场力而已。正所谓“电学搭台，力学唱戏”。本题不涉及计算电场力做功的多少，只要求用电势求电势能，由动能求速度等，我们可以不用动能定理求解，直接用只有电场力做功，动能和电势能总和守恒求解。

【例2】(“动能+重力势能+电势能”守恒)如图2，一带负电荷的油滴在匀强电场中运动，其轨迹在竖直面(纸面)内，且相对于过轨迹最低点P的竖直线对称。忽略空气阻力。由此可知

( )

图2

A.Q点的电势比P点高

B.油滴在Q点的动能比它在P点的大

C.油滴在Q点的电势能比它在P点的大

D.油滴在Q点的机械能比它在P点的小

【答案】AB

【解析】由于油滴轨迹相对于过P的竖直线对称且合外力总是指向轨迹弯曲内侧，所以油滴所受合外力沿竖直向上的方向，因此电场力竖直向上，且qE>mg，则电场方向竖直向下，所以Q点的电势比P点的高，A选项正确；当油滴从P点运动到Q点的过程中，电场力做正功，电势能减小，C选项错误；由于只有重力和电场力做功，动能、重力势能和电势能总和守恒，因为P点的电势能大于Q点的电势能，所以Q点机械能大于P点的机械能，同时合外力做正功，动能也增加，所以Q点动能大于P点的动能，B正确，D错误。

【点评】例1的小球在水平面内运动，不会涉及重力势能的改变，本题油滴(计重力)在运动过程中的动能、重力势能、电势能都在相互转化，但只有重力和电场力做功，带电油滴的机械能和电势能总和守恒，本题同样不涉及重力、电场力做功的多少，只需要知道能量的变化，这种不考虑力做功多少，只求解能量转化的题目，用能量守恒定律比用功能关系更简单。

【例3】(“动能+弹性势能+电势能”守恒)如图3所示，一绝缘轻弹簧的左端固定，右端与一带电小球相连接，小球静止在光滑绝缘的水平面上，施加一个水平方向的匀强电场(图中未画出)，使小球从静止开始向右运动，则向右运动的这一过程中(运动过程中始终未超过弹簧的弹性限度)由此可知

( )

图3

A.小球动能最大时，小球电势能和弹性势能总和最大

B.弹簧弹性势能最大时，小球和弹簧组成的系统机械能最大

C.小球电势能最小时，小球动能为零

D.当电场力和弹簧弹力平衡时，小球的动能最大

【答案】BCD

【解析】小球运动过程中只有电场力和弹簧弹力做功，故小球的电势能、动能和弹簧的弹性势能总量守恒，小球动能最大时，小球电势能和弹性势能总和最小，故A错误；在最右端，弹簧弹性势能最大，电势能最小，故小球和弹簧组成的系统机械能最大，故B正确；小球向右运动时，电场力做正功，电势能减小，故最右端电势能最小，此时动能为零，故C正确；当电场力和弹簧弹力平衡前，电场力大于弹簧的弹力，小球做加速运动，当弹力等于电场力时，速度达到最大，小球的动能最大，故D正确；故选BCD。

【点评】在例题中用弹性势能代替重力势能，即只有电场力和弹簧弹力做功，带电小球的电势能、动能和弹簧的弹性势能总和守恒。其目的是不考虑力做功多少的情况下，求解能量转化的题目时，用能量守恒定律比用功能关系解题更简单。

【例4】(“动能+重力势能+弹性势能+电势能”守恒)如图4所示，绝缘轻质弹簧的下端固定在斜面底端，弹簧与斜面平行，带电小球Q(可视为质点)固定在光滑绝缘斜面上的M点，且在通过弹簧中心的直线ab上。现把与Q大小相同，带电性也相同的小球P，从直线ab上的N点由静止释放，在小球P与弹簧接触到速度变为零的过程中

( )

图4

A.小球P的速度先增大后减小

B.小球P和弹簧的机械能守恒，且P速度最大时所受弹力与库仑力的合力最大

C.小球P的动能、重力势能、电势能与弹簧的弹性势能的总和不变

D.弹簧弹性势能的增加量等于小球P的重力势能和电势能的减少量

【答案】AC

【解析】小球P与弹簧接触时，沿平行斜面方向受到小球Q对P的静电力、重力的分力、弹簧的弹力，开始时合力的方向沿斜面向下，速度增加，后来随着弹簧压缩量变大，合力的方向沿斜面向上，速度逐渐减小，A正确；小球运动过程中只有静电力、重力和弹簧弹力做功，故小球的电势能、动能、重力势能和弹簧的弹性势能总量守恒，C正确，B错误；初末位置弹簧弹性势能的增加量等于小球P的重力势能和电势能的减少量，但过程中有动能参与转化，D错误。

【点评】为了将带电小球的能量转化进一步扩大，本题设计了四种能量相互转化，即小球的电势能、动能、重力势能和弹簧的弹性势能相互转化，只有电场力、重力和弹簧弹力做功，小球的电势能、动能、重力势能和弹簧的弹性势能总和守恒。这样高中物理所涉及的宏观物体受到的保守力做功，相对应的能量守恒定律，共有七种情况。