“电场+动量”多元命题的思路和解读

福建

(作者单位：福建省福鼎市第一中学)

情境、多元、能力——建构学科综合素养本位

“电场+动量”问题即以带电体在电场中的运动为试题主体情境，动量定理或动量守恒定律为必要解题环节，实现学科内不同分支知识有效互联的一种试题多元编制方式。这类试题要求学生对于不同知识模块要融会贯通，不仅要了解电场的知识框架，而且会灵活应用动量定理、动量守恒定律和能量守恒定律分析电场中的动力学、功能关系，研究带电体在电场中的运动规律，因此有一定的综合性，对学生能力的考查也呈现多维化，在试题中常以压轴题的形式出现。下面对《考试大纲》框架内电场与动量的综合命题思路进行梳理，供大家参考。

试题编制一 带电导体球碰撞型问题

设计思路：基于两个或两个以上的带电导体球在电场中的运动创设静电学试题情境，以导体球碰撞问题为纽带关联动量守恒定律等动力学、功能知识。

试题解读：(1)导体球碰撞瞬间分为弹性碰撞或非弹性碰撞，不论为何种碰撞类型，导体球是否带电，由于作用持续的时间极短，相互作用力很大，可认为内力远大于外力，因此碰撞过程符合动量守恒；若发生弹性碰撞，碰撞前与碰撞后总动能相等；若为非弹性碰撞，系统的总动能减少；如果发生完全非弹性碰撞，系统的总动能损失为最大值。(2)导体球接触瞬间电子在导体球间发生转移，符合电荷守恒定律，导致电荷会在导体球间重新分配，接触后电荷分布的规律有：

①两个完全相同的导体球接触，若为同种电荷则平分原来所带电荷量的总和；若为异种电荷则先中和再平分；

②一个大导体球和一个小导体球接触，且小导体球半径远小于大导体球半径，可忽略不计，则接触后电荷全部集中于大导体球上，小导体球呈中性。

③两个半径不同的导体球接触，两球静电平衡为等势体，根据导体表面电势相等关系，可知接触后两球分布电荷量与半径成正比。

图1

(1)甲、乙两球碰撞后瞬间，乙球的速度v2的大小；

(2)小球乙落在D点时，甲、乙两小球之间的距离s；

(3)若只改变场强E的大小，为了保证乙球能沿竖直轨道运动，并通过C点后落到水平轨道AB上，试确定场强E的取值范围，设乙球从B点运动到C点的过程中，电势能的变化量为ΔEp，在图2的坐标系中，定量画出小球乙的电势能变化量ΔEp与场强E的关系图象。(画图时不必说明理由)

图2

【解析】(1)设甲球和乙球碰撞后的速度分别为v1、v2，由动量守恒定律和机械能守恒定律可得

mv0=mv1+mv2

(2)设乙球经过C点时的速度为v3，由动能定理可得

解得FN=0.45 N

乙球离开C点后做类平抛运动，设加速度为a，运动时间为t，水平位移为x，得

联立解得x=2 m

因甲球在这一过程中的速度v1=0，所以s=x=2 m，甲、乙两小球之间的距离为2 m。

(3)乙球能够运动到C点的条件是FN≥0，

解得E≥600 V/m

为保证碰撞前甲球在轨道AB上运动，需满足的条件是Eq≤mg，解得场强的最大值为E≤1.5×103V/m，所以场强的取值范围为600 V/m≤E≤1.5×103V/m

乙球由B点沿轨道运动至C点的过程中，电场力做正功，电势能减小

ΔEp=-W=2Eq1R

解得ΔEp1=-0.06 J，ΔEp2=-0.15 J

其电势能变化量ΔEp与场强E的关系如图3所示

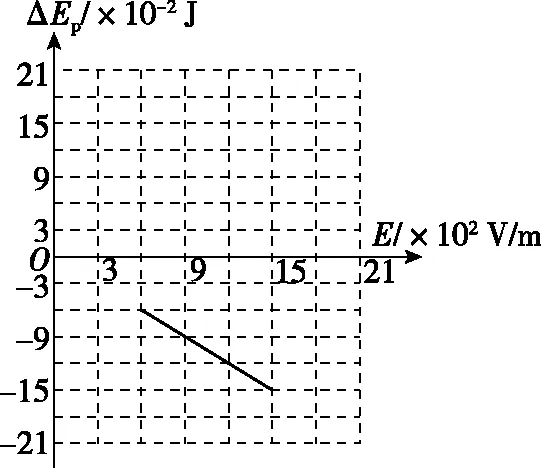
图3

【点评】小球甲、乙发生弹性正碰，动量守恒，机械能守恒，结合动量守恒定律和机械能守恒定律求出碰撞后瞬间小球乙的速度，碰撞瞬间根据导体球电荷分布规律可知两球电荷量平均分配，本题以电场中的导体球为载体很好地将电场力、能的性质和动量守恒融合为一体；小球乙在圆形轨道中的运动为圆周运动，根据动能定理和牛顿运动定律求出小球乙通过C点的速度和轨道对它的压力大小，离开C点后小球做匀变速曲线运动，运用运动的合成与分解，可分析竖直方向上的运动时间和水平方向上的位移；为了保证小球乙能沿轨道运动并通过C点，过C点时压力大于等于零，抓住电场力小于重力，结合动能定理求出电场强度的范围，由电场力做功与电势能变化之间的关系可求出ΔEp的最大值和最小值，作出ΔEp-E图象。本题考查了动量守恒定律、机械能守恒定律、动能定理、牛顿第二定律的综合运用，综合性较强，在处理小球圆周运动和匀变速曲线运动时，要注意电场力的作用及做功情况。

试题编制二 带电液滴结合型问题

设计思路：以带电液滴为主要研究对象，与多滴液滴或其他带电体构成作用系统创设试题主体支架，以液滴在电场中的运动过程为试题情境，研究液滴结合瞬间的动力学、功能关系问题。

试题解读：带电液滴结合瞬间与其他带电体融合为一个整体，若结合瞬间不计重力、电场力等系统外力的影响，可近似认为发生完全非弹性碰撞，符合动量守恒定律，结合为一体后，液滴的总质量为结合前液滴的质量之和，电荷量为结合前液滴各自所带电荷量的代数和。

【例2】真空中存在电场强度大小为E1的匀强电场，一带正电油滴a在该电场中竖直向上做匀速直线运动，速度大小为v0，在油滴处于位置A时，电场强度的大小突然增大到某值，但保持其方向不变。持续一段时间t1后，到达某位置B点，在B处与一质量相同的中性油滴b相碰，并立即结合成大油滴(中性油滴的速度忽略不计，结合瞬间不计重力、电场力的影响)，同时突然将电场反向，但保持其大小不变；再持续同样一段时间后，油滴运动到C点，重力加速度大小为g，求：

(1)油滴运动到C点时的速度；

(2)求增大后的电场强度的大小；为保证后来的电场强度比原来的大，试给出相应的t1和v0应满足的条件。已知不存在电场时，油滴以初速度v0做竖直上抛运动的最大高度恰好等于C、A两点间距离的两倍。

【解析】(1)设油滴a质量和电荷量分别为m和q，油滴速度方向向上为正。油滴在电场强度大小为E1的匀强电场中做匀速直线运动，故匀强电场方向向上，在t=0时，电场强度突然从E1增加至E2时，油滴做竖直向上的匀加速运动，加速度方向向上，由动量定理得

E2qt1-mgt1=mv1-mv0

油滴a和油滴b相碰瞬间，由动量守恒定律得mv1=2mv2

电场强度在时刻t1突然反向，油滴做匀变速直线运动，加速度方向向下，由动量定理得

-E2qt1-2mgt1=2mv3-2mv2

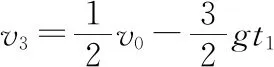
(2)由题意知在t=0时刻前有E1q=mg，在t1时间内，加速度大小a1满足E2q-mg=ma1

在t1时刻后，加速度大小a2满足E2q+2mg=2ma2，油滴在从时刻t1到油滴运动到C点时间内的位移为

【点评】对于带电体在匀强电场中的运动问题，可以从两条线索展开：一是力和运动的关系，根据带电体受力情况，利用牛顿第二定律结合运动学公式或用动量定理确定带电体的速度、时间和位移等；二是功和能的关系，根据电场力对带电体做功，引起带电体的能量发生变化，利用动能定理进行解答，在关联时间的前提下一般优先考虑动力学方程或动能定理，当然在选择动力学公式时要注意带电体的运动条件—匀变速直线运动；油滴的结合瞬间，由于不计重力、电场力的影响，符合动量守恒定律，利用动量守恒定律求解。

试题编制三 带电体相互作用型问题

设计思路：相互作用的带电体间发生相对运动时，带电体间的电场力为系统内力，若系统所受合外力为零，符合系统动量守恒定律，可以以此模型结合带电体运动设计“电场+动量”问题。

试题解读：带电体孤立系统相互作用过程中，电场力为内力，动量守恒；通过电场力做功，系统的动能和电势能相互转化，可应用能量守恒定律综合分析问题；关联运动的动态分析，带电体往往会出现临界状态，要注意隐含条件的采集和研究，如电势能最大时系统内各物体的速度相同等。

图4

(1)若两个带电小球逐渐靠近，带电小球A的电势能如何变化；

(2)如果A不会超过B，计算A、B间的最小距离；

(3)若让A能够超过B，求B最终的速度？

【解析】(1)两带电小球逐渐靠近，电场力做负功，A带电小球的电势能逐渐增大；

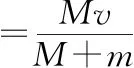
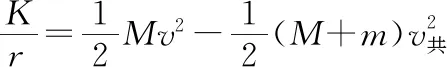
(3)A超过B后，由于球间电荷产生的排斥力，两球的间距逐渐增大，最终距离会趋向无穷远，两带电小球的电势能趋近于0，由动量守恒定律得Mv=MvA+mvB

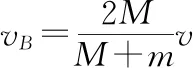
【点评】A、B运动过程中，系统动量守恒，因此解题切入点要明确依据动量守恒定律和能量守恒定律，如果A球不会超过B，A初动能全部转化为两者的动能和系统的电势能，根据临界条件、动量守恒定律以及能量守恒定律列式求解；若A超过B，根据动态分析研究两球最终的稳态，运用动量守恒定律和能量守恒定律求解，在运用能量守恒定律时要注意电场力做功与电势能变化的关系。

试题编制四 动体模型拓展问题

设计思路：以力学中常见的动量守恒模型为载体，承载电荷构建带电体运动的动体系统模型，从动力学、功能角度研究系统中带电体和其他物体的运动。

试题解读：以动体模型为载体组成的孤立系统中，带电体间会发生相对运动，电场力可能为系统外力，也可能为系统内力，带电体间的滑动摩擦力为内力，若系统所受的合外力仍为零，系统动量守恒，通过电场力、摩擦力做功，系统的机械能和电势能、热能间相互转化。可以以动量守恒定律和系统功能关系联立求解，但要注意守恒条件的判定。

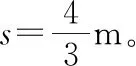
图5

(1)A与B相碰前的速度为多大；

(2)要使C刚好不脱离滑板，滑板的长度应为多少；

(3)在满足(2)的条件下，求最终A、B的距离满足的关系式？

【解析】(1)A与B相撞之前由动能定理

代入数据得v0=4 m/s

(2)A与B相碰后速度为v1，由动量守恒定律得

C在A上滑行时，A、B分离，B做匀速运动，A与地面的摩擦力f2=μ2(m+M)g=0.8 N，A受到的电场力F=qE=0.8 N，故A、C系统动量守恒，当C刚好滑到A左端时共速v2，由动量守恒定律有mv1=(m+M)v2，得

设A长度为L，则由系统功能关系有

代入数据得L=0.5 m

(3)对C由牛顿第二定律可知μ1Mg=Ma，

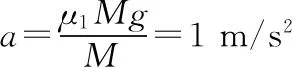
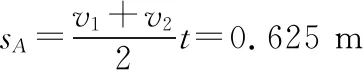
0.5 s内B的位移sB=v1t=1 m

两者以后距离关系式为

x=sB-sA+(v1-v2)t=0.375+1.5t

【点评】本题的编制设计仍基于力学的板块模型，再从力、能的角度融合电场的相关知识。A与B相碰后，C在A上滑行时，A、B分离，B做匀速运动，根据动量守恒定律求出C滑上A时A的初速度。C滑上A后，A所受地面的摩擦力与所受的电场力大小相等，方向相反，A、C系统符合动量守恒的条件，结合动量守恒定律和能量守恒定律可求出滑板的长度；结合牛顿第二定律和运动学公式求出C在A上滑行的时间和A、C一起运动的速度，从而求出A、C速度相同时，A、B的距离。本题综合考查了动能定理、动量守恒定律、能量守恒定律以及牛顿第二定律和运动学公式，综合性较强，关键于在理清物体的运动情况，选择合适的规律求解。