基于第一性原理的钙钛矿材料空位缺陷研究

袁海东，周 龙，苏 杰，林珍华，常晶晶，郝 跃

(西安电子科技大学 微电子学院，陕西 西安 710071)

1 引 言

近年来，有机-无机杂化钙钛矿材料由于具有光吸收率强，迁移率高，载流子寿命长，带隙可调以及加工方式多样等优点,在太阳能电池，OLED(Organic Light Emitting Doide)，光探测器等领域中展现出了巨大的潜力，已经成为国内外研究热点[1-7]。尤其在太阳能电池领域，自2009年首次报道以来，基于有机-无机钙钛矿材料的太阳能电池能量转换效率已从3.8%增加到23.7%[8-11]，已经远远超过商业化所期望的能量转换效率门槛(10%)，这使得有机-无机杂化钙钛矿材料变得更加具有竞争力。此外，有机-无机钙钛矿材料可以采用溶液法制备，并且可以与印刷工艺相结合，从而极大地节省生产成本，加快制备周期[12]。同时，有机-无机钙钛矿材料可沉积于柔性基底，这进一步拓展了其应用范围[13-14]。有机-无机钙钛矿材料的分子式符合AMX3(A 为有机阳离子，M为Pb，Sn等阳离子，X为I，Br，Cl 阴离子)结构，通过不同组分和不同元素的掺杂等方式能够有效地改变其材料特性，例如电荷复合速率，载流子扩散长度和界面的能级势垒。研究发现通过掺杂Cl和Br元素能够改变钙钛矿材料的带隙，随着Br比例的提升，其带隙越来越大[15-18]。目前，为了避免铅的毒性，钙钛矿材料无铅化已成为钙钛矿材料研究领域的新热点。研究发现用Sn取代Pb元素可以有效避免毒性，同时保持相对良好的器件效率[19-20]。同时，研究者提出通过掺杂过渡金属和多价金属阳离子能够有效地改变钙钛矿材料的电学和光学特性，对于材料薄膜的制备和器件性能的提升具有显著作用[21-24]。

目前，相继有研究者报道过量的PbI2能够有效钝化钙钛矿材料晶界，同时提高器件性能[25-26]。Hong等人[27]发现由于钙钛矿材料的本征点缺陷不会产生间隙态，同时其缺陷态会以自掺杂方式改变材料的特性，故通过溶液法制备的多晶钙钛矿薄膜材料可以成为优异的光电材料。尽管有机无机杂化钙钛矿材料作为新型优异的光电材料，在光电器件领域具有广泛的研究和应用，但对于空位缺陷自掺杂钙钛矿材料的电子结构和光学性质的微观作用机理研究鲜有报道。本文基于密度泛函理论的第一性原理计算方法，从微观电子层研究缺陷自掺杂钙钛矿的电子结构和光学性质，初步揭示其自掺杂对钙钛矿材料性质变化的微观机理，为钙钛矿材料实验研究提供理论指导。

2 模型构建和计算方法

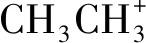
采用Materials Studio 8.0软件的CASTEP模块，基于广义梯度近似方法(GGA) 和PBE泛函，对1×2×1的超晶胞模型进行结构优化和计算。结构优化和能量计算选用的平面波截止能量为500 eV，K空间点选用4×3×4，而且考虑采用范德华力修正和自旋轨道耦合作用(SOC)进行能量计算。同时，每个原子的自洽收敛标准为1×10-5eV, 能量变化范围不超过1×10-5eV，晶体内应力不大于0.05 GPa。布里渊区的积分使用Monkor-Pack方案进行。计算时每个原子上的力不大于0.3 eV/nm。

图1 本征钙钛矿和空位缺陷钙钛矿的电子结构 Fig.1 Electronic structures of intrinsic perovskites and perovskites with vacancy defects

3 钙钛矿的电学特性

3.1 钙钛矿的电子结构

通过对空位缺陷的几何结构进行优化，得到其超晶胞模型的晶格常数，键长和键角。如表1所示，本征钙钛矿材料优化模型的晶格常数和实验值的晶格常数非常符合，说明本文构建的模型与实验一致，这是后续计算分析的基础。同时也说明构建的空位缺陷结构非常稳定。对比Pb空位缺陷和本征结构之间的不同，可以看出晶格常数都变小了，这是因为失去了一个Pb原子，存在一个空位缺陷。同时，因为Pb原子的半径较大，失去Pb原子后，其晶格变化比较明显，Pb-I的键长也减小了，在键角方面，因为缺陷的存在，导致其键角减小了很多。而对于I空位缺陷钙钛矿的晶格常数基本未变，Pb-I的键长也没有太大变化。这是因为I原子的半径相对较小，虽然失去了一个I原子存在一个空位缺陷，但是这种缺陷是可以被容纳的。但是由于I空位缺陷的存在，键角减小了很多。

表1 本征钙钛矿和空位缺陷钙钛矿的晶格常数、键长和键角

为了更好地证明本文构建的缺陷体系的稳定性，需计算出缺陷自掺杂体系的形成能。形成能的值越小，说明自掺杂体系越稳定，这种自掺杂方式越可能在晶体中存在。本文计算形成能量的表达式为：

ΔE=E(CH3NH3PbI3)vacancy-

E(CH3NH3PbI3)+μ(X) ,

(1)

其中，E(CH3NH3PbI3)vacancy和E(CH3NH3PbI3)分别是缺陷体系的总能量和本征钙钛矿材料的能量，μ(X)是元素Pb、I的化学能。通过计算得到不同空位缺陷对应的形成能，如图2所示，可以看到，Pb空位和I空位缺陷钙钛矿材料的形成能都是负值，形成能越小说明缺陷自掺杂的电子结构越稳定。

图2 空位缺陷钙钛矿材料的形成能 Fig.2 Formation energy of perovskites with vacancy defects

3.2 本征钙钛矿材料的能带和态密度

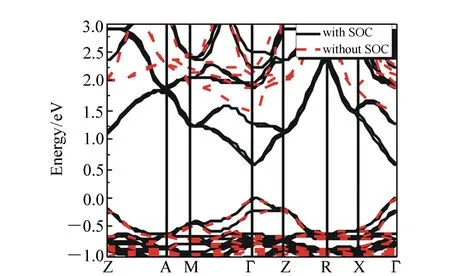
图3 本征钙钛矿材料的能带图 Fig.3 Energy band structure of initial perovskites

通过优化和计算本征钙钛矿材料结构，对比考虑SOC作用和采用范德华力修正两种计算方法的计算结果，并给出其对应的能带结构图，如图3所示。由图3可知，本征钙钛矿材料是直接带隙半导体，其禁带宽度为1.52 eV，与实验值1.57 eV基本相近。由于Pb2+是重金属离子，在理论计算中需要考虑SOC，才能够准确计算能带变化以及进行其他物性研究。然而，考虑SOC后，计算得到的带隙仅为0.57 eV，远远低于实验值。这主要是因为传统的密度泛函理论近似计算不能准确描述重金属离子的f态，进而导致所计算的钙钛矿材料的禁带宽度偏低。准确的带隙值对于材料物性分析非常重要，但考虑SOC的作用后，其计算量增大很多，计算成本也将增加很多。针对这一问题，本文通过采用GGA-PBE的方法和范德华力修正，得到准确的带隙值，同时采用范德华力修正能够节约计算成本和时间。更重要的是，可以看到不管是否考虑SOC的作用，两者的能带变化和趋势是一致的，所以对于其物性研究没有影响。因此，为了在准确的带隙下研究钙钛矿材料特性，本文采用范德华力修正，以得到更加准确的带隙。本征钙钛矿材料导带顶的最低点同价带顶最高点位于同一Γ点，说明钙钛矿材料是直接带隙的宽禁带半导体材料。

为了进一步研究钙钛矿的微观机理，需要结合能带图和态密度图，详细分析电子对能级的贡献。图4是计算出的本征钙钛矿材料的态密度图。结合能带图和态密度分析，可明显看出价带的3个主要区域，以及位于费米能级以上的1.7～3.8 eV的导带区域。价带区域的能级很窄，非常缓慢平滑，而导带区域较宽，波动较大，这表明导带中的电子有效质量很小，非局域密度起着很大的作用，组成导带的原子轨道组分是高度可扩展的。在计算得到的能带图中导带部分则主要是来源于Pb 6p态电子和I 5s态电子的杂化作用。

图4 本征钙钛矿材料的态密度 Fig.4 Density of state for intrinsic perovskites

从图中可以清楚地看出，Pb 6p态电子容易跃迁到I 5s态，导致I位局域态密度中心向低能级移动，表明钙钛矿材料具有很强的离子特性，且共价键的相对作用较弱，所以钙钛矿材料是混合键型化合物。

从态密度图可以看出，上价带区Pb 6s态电子与I 5p态电子的重叠程度非常大，表明Pb 6s态电子和I 5p态电子在上价带区发生非常强烈的电子轨道杂化。而在下价带和偏远价带区域，Pb 6s态电子和I 5p态电子重叠的部分比上价带区域小很多，这表明Pb 6s态电子和I 5p态电子在下价带区域内杂化程度比较低。

3.3 空位缺陷钙钛矿的能带和态密度

基于前面本征钙钛矿能带的分析，采用范德华力修正，得到相应的空位缺陷自掺杂钙钛矿的能带图，如图5所示。由图5可知，Pb空位缺陷型钙钛矿材料，在失去一个Pb原子后，其费米能级下移进入价带，形成偏P型钙钛矿材料；相反，对于I空位缺陷钙钛矿材料，失去一个I原子后，其费米能级上移进入导带，形成偏N型钙钛矿材料。同时，本文也计算考虑SOC作用后得到的能带图。通过对比发现，在SOC作用下，导带会下移，其带隙会比准确带隙偏低，这是由于传统GGA方法低估了带隙。尽管如此，采用范德华力修正后，其带隙明显得到提升，同时其价带和考虑SOC价带的变化趋势基本一致，也说明空位缺陷自掺杂能带图的准确性。

图5 空位缺陷钙钛矿的能带图 Fig.5 Band structures of perovskties with Pb and I vacancy defects

为了进一步探究空位缺陷对钙钛矿能带的影响，本文计算出了Pb、I空位缺陷钙钛矿材料的态密度图，如图6所示。对于Pb空位缺陷，可以明显看到费米能级进入价带，进一步证明Pb空位缺陷属于P型材料。同时，其导带区域(2～4 eV)主要是由Pb的p态和I的s态电子贡献；对于上价带区域(-4～0 eV)则主要是由I的p态和Pb的s态电子贡献；而下价带区域部分(-8～-6 eV)主要是由Pb的s态和I的p态电子的杂化作用形成的。通过分析态密度，其变化趋势和能带基本是一致。

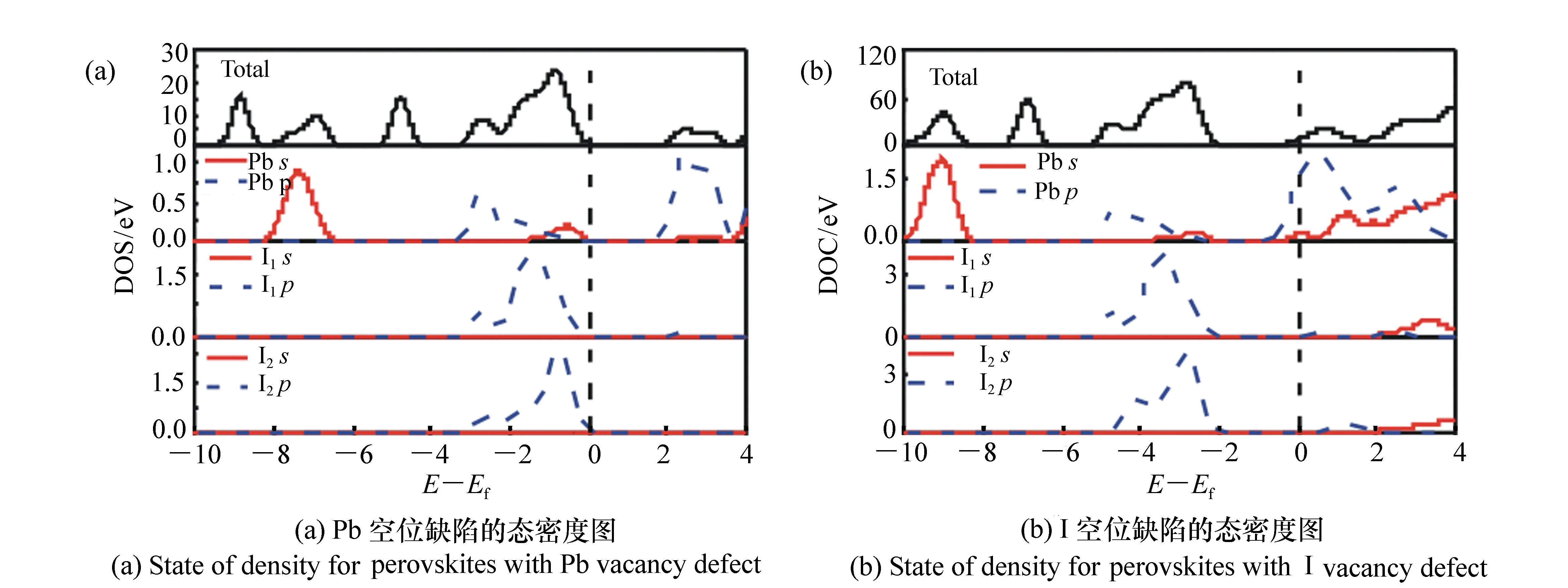
图6 空位缺陷钙钛矿的态密度图 Fig.6 Density of state for perovskites with Pb and I vacancy defects

3.4 空位缺陷钙钛矿的差分电荷密度图

分别计算并绘出本征钙钛矿和空位缺陷钙钛矿的差分电荷密度图，如图7所示(彩图见期刊电子版)，进一步论证各个原子的电子得失能力。在本征钙钛矿中，Pb和I原子的电荷与纯离子的相互作用有显著偏差，表明Pb-I有共价键和离子键的组合，这也可以解释为何Pb 6s、6p电子和I的5s电子在价带顶部有一个共价键。差分电荷图中，Pb原子周围是黄色，表明Pb易失去电子，I附近是蓝色表明其易得到电子，颜色深浅表明得失电子能力的强弱。结合上文的态密度图可以看出，本征钙钛矿材料的总态密度主要是Pb 6p态电子和I 5s态电子的贡献。

对于Pb空位缺陷钙钛矿材料，Pb有失去电子的趋势；I原子有得到电子的趋势，其主要得失的都是s和p态电子，Pb原子s和p态得到电子，I原子s和p态失去电子。差分电荷密度图中，明显缺失了一个Pb原子，Pb失去电子，I得到电子，正好和电荷分布的分析相符合。

对于I空位缺陷钙钛矿材料，Pb有失去电子的趋势，但是与本征钙钛矿相比，其失去电子能力较低，同时I原子也有得到电子的趋势，相比于本征钙钛矿，其能力也较低。主要的得失电子变化都是s和p态电子，d态都没有变化。同样，在差分电荷密度图中，明显缺失了一个I原子，Pb失去电子，I得到电子，正好和电荷分布的分析相符合。

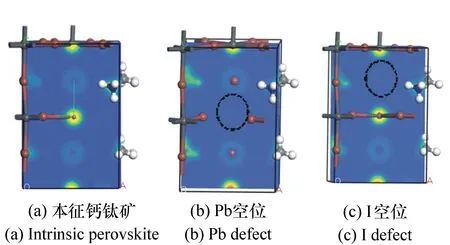
图7 本征钙钛矿和空位缺陷钙钛矿的差分电荷密度图 Fig.7 Difference charge densities of intrinsic perovskites and perovskites with vacancy defects

4 钙钛矿的光学特性

此外，本文计算了Pb和I空位缺陷型钙钛矿材料的光学性质，其理论部分源自固体光学公式。使用线性响应的光介电常数来更好地描述固体的宏观光学响应函数。在这里，ε1、ε2表示介电函数的实部和虚部。通过使用Krams-Clonish色散关系和直接转移概率的定义，可以很容易地导出介电函数的实部、虚部、吸收系数、反射系数和能量损失。

这里直接给出相应的推导结果：

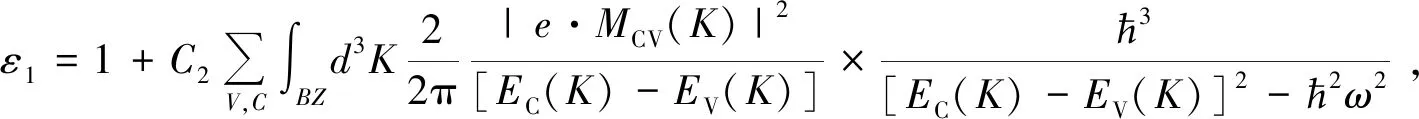
(2)

(3)

(4)

(5)

(6)

上式中，导带和价带分别用C和V表示，第一布里渊区用BZ表示，ћ是狄拉克常数，K为空间倒格矢，ω为角频率，|eMcv(K)|2为动量矩阵元。上述公式是理论分析晶体能带结构和光学性质的主要依据，其反映的内容是电子跃迁引起的光谱发光机理。这种分析方法可以用来表征材料的物理性质，并可以与物理相互作用过程中的微观电子结构和微观模型相结合。

图8 钙钛矿材料的光学特性 Fig.8 Optical properties of perovskites

图8(a)为计算得到的本征钙钛矿和Pb、I空位缺陷钙钛矿介电函数虚部，从图中可以看出，本征钙钛矿材料的虚部有3个主要的峰值，这些峰分别出现在3.0、7.0和14.7 eV。在3.0 eV处的峰主要由远离价带顶部的Pb 6s态与高价带底部的I 5p态之间的光学跃迁引起；在7.0 eV的峰值是由于价带顶部的Pb 6s态和上价态I 5s态之间的电子跃迁引起的；在14.7 eV处的峰值是由于价带顶部的Pb 6s态和导带顶部的I 5p态之间的跃迁引起的。而Pb、I空位缺陷钙钛矿的介电函数图中则出现4个峰，且相比本征钙钛矿材料而言，其在近红外区域有明显的峰。这个峰主要是由于费米能级进入导带或价带，电子更容易发生跃迁所导致的。在7 eV和14.7 eV附近的峰基本没有变化，相反，在3 eV附近，空位缺陷钙钛矿的峰则有明显提升，这主要归因于Pb原子和I原子之间的光学跃迁，包括Pb 6p和I的5s态电子之间的跃迁。这可以从图6中的Pb空位缺陷和I空位缺陷钙钛矿分态密度中看到。

图8(b)为本征、Pb、I空位缺陷钙钛矿材料的光学吸收谱。从图中可以明显看出，本征钙钛矿材料的光吸收峰分别位于3.7 eV和8.8 eV。且本征钙钛矿材料的光吸收边约为1.52 eV，这与图3中所计算的带隙相对应，即价带顶的电子跃迁至导带底所需要的能量。当存在Pb或I空位缺陷时，其吸收边发生明显的蓝移，这一结果与介电函数虚部的变化相对应。值得注意的是，在0.67 eV的地方存在一个近红外区间隙带隙。这应该主要是由于费米进入导带或价带，部分电子更容易跃迁，所以在近红外区域出现小的吸收峰。

5 结 论

本文基于第一性原理计算研究了空位缺陷自掺杂对钙钛矿电子结构及光学性质的影响，从微观电子层次解释自掺杂对钙钛矿的电学和光学性质的影响机制。研究表明通过采用范德华力修正，解决密度泛函理论的低估带隙的问题，得到与实验值相近的禁带宽度值1.52 eV。同时，研究发现空位缺陷能够改变钙钛矿的材料特性，Pb空位缺陷会导致钙钛矿材料呈现P型属性；而I空位缺陷会导致钙钛矿材料呈现N型属性。在光学方面，空位体系会增大其介电函数，同时在近红外区域出现一个小的吸收峰。此外，由于缺陷态自掺杂作用，其吸收谱会出现蓝移现象。通过研究分析发现，空位缺陷自掺杂作用对钙钛矿的光学特性具有较好的调控作用，对于钙钛矿的物性研究及其在光电器件领域的应用具有重要的理论价值。