跳跃-滑翔弹道扰动引力自适应网格快速赋值方法*
2019-10-14王顺宏戴陈超杨奇松
王顺宏,戴陈超,李 剑,杨奇松
(火箭军工程大学 作战保障学院, 陕西 西安 710025)
随着弹道导弹制导工具误差的不断减小,制导方法误差的影响日益突出,而扰动引力是影响制导方法误差的主要因素。对于滑翔距离超过12 000 km 的高超音速滑翔导弹,扰动引力影响滑翔段弹道所产生的落点偏差达到千米量级。因此,必须提高滑翔导弹制导计算机中扰动引力赋值精度。同时,由于弹载计算机存储空间有限,应当尽可能减小扰动引力赋值所需的数据存储量。另外,由于是弹上实时计算,对计算速度也提出了较高的要求,传统扰动引力赋值方法(如点质量法、球谐函数法等)无法同时满足计算精度、存储量和计算速度的要求,因此必须针对跳跃-滑翔弹道开展高精度扰动引力快速赋值方法研究。
数值逼近方法是高精度扰动引力快速赋值的主要方法,对于主动段的扰动引力,文献[1]通过拉格朗日插值模型,利用有限元方法逼近扰动引力;文献[2]提出了广义延拓逼近算法在扰动引力快速赋值中的应用;文献[3-4]分别采用了神经网络逼近算法和三次等距B样条函数方法,以上方法对于主动段扰动引力均取得了较好的逼近效果;文献[5]针对弹道导弹全程提出了“漏斗形”有限元单元构建方法,将有限元方法扩展到被动段扰动引力快速赋值中,取得了较好的效果;文献[6]采用球谐函数换极法研究被动段扰动引力快速赋值,在保证精度的前提下,提高了赋值速度,但是仍然不能满足弹上实时计算的要求。对于跳跃-滑翔弹道的扰动引力快速赋值,上述方法均有一定的借鉴意义,但仍存在以下不足:第一,传统弹道导弹的再入段通常忽略扰动引力的影响,研究重点集中于主动段与被动段,但跳跃-滑翔弹道属于再入段,此时导弹在临近空间内以高超音速滑翔,其弹道特性与上述文献所研究的弹道导弹弹道特性存在较大差异。因此上文提及的快速赋值方法在跳跃-滑翔弹道的适用性需做进一步分析。第二,文献[2]中广义延拓逼近算法相对于一般方法精度大幅提高,但也增加了数据存储量,同时由于跳跃-滑翔弹道的弹道轨迹较长,若按照传统方法进行网格划分同样会导致网格数量较多,数据存储量加大。
1 基本思路
传统基于有限元法的扰动引力快速赋值是将参考弹道附近空域进行有限元划分,建立以参考弹道为中心的飞行管道,确定各单元节点并对节点进行赋值,而后根据导弹实时位置判断所在单元,通过插值算法,快速计算当前位置的扰动引力值。
众所周知,对于有限元方法而言,单元划分的大小直接决定了求解精度以及存储的节点数目,考虑到上文提及的跳跃-滑翔弹道的特殊性,传统划分方式将导致较大的弹上数据存储量。基于上述考虑,提出跳跃-滑翔弹道扰动引力自适应网格赋值模型,在保证赋值精度的同时,通过增加单元格边长,从而减少单元格划分数量,降低弹上存储量。基本思路如下:
1)根据发射任务,在不考虑扰动引力等干扰因素下确定一条参考跳跃-滑翔弹道;
2)根据参考弹道将附近空域进行有限元划分,以参考弹道为中心建立较大的一级网格单元,并采用球谐函数法对一级单元节点的扰动引力赋值;
3)导弹进入跳跃-滑翔段之后,根据导弹实际位置坐标确定所在一级单元,并在一级单元内部在线生成包含该点的自适应二级单元(以下简称二级单元);
4)根据一级单元节点的扰动引力值,采用基于反距离加权的广义延拓逼近算法计算二级单元节点扰动引力值,然后根据二级单元节点值,采用拉格朗日插值法快速计算导弹当前位置的扰动引力值;
5)对于新的待求点,先判断是否属于当前的二级单元,若在其内部,直接通过该二级单元计算扰动引力值,反之,转第3步。
2 自适应网格构建模型
文献[7]中基于发射坐标系对被动段弹道进行了单元划分,该方法的优点在于整体坐标与局部坐标的转换较为简单,并且提高了搜索效率。由于本文只考虑跳跃-滑翔段弹道的扰动引力计算,因此将发射坐标系平移至跳跃-滑翔段弹道下方,其原点与起始滑翔点延地心矢径方向在地球表面的投影重合,各坐标轴方向均不变,此时称该坐标系为再入滑翔段坐标系,简称再入段坐标系,本文将在此坐标系内基于基准弹道构建单元。
2.1 一级单元构建及节点确定
在再入段坐标系内设定空域Ω并进行划分,按照直角坐标(x,y,z)截取六面体单元Ωe,Ωe可由3组坐标区间表示为{[x1,x2],[y1,y2],[z1,z2]},同时Ωe的8个节点坐标为(xi,yi,zi)(i=1,2,3,…),如图1所示。
图1 一级单元空域划分示意图Fig.1 Schematic diagram of the first level grid space division
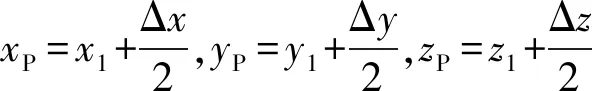
(1)
通过导弹在再入段坐标系中的位置坐标即可确定其所在的一级单元。
2.2 自适应二级单元构建及节点确定
自适应二级单元的构建是根据导弹所处的一级单元以及在再入段坐标系中的坐标在线生成的,具体步骤如下:
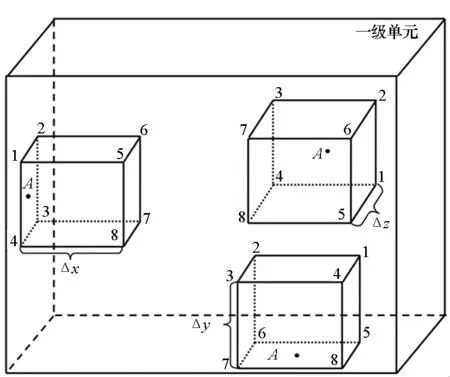
步骤1:根据导弹的全局坐标A(xA,yA,zA)确定其所处的一级单元格j,单元格j的坐标区间可以表示为{[xj,1,xj,2],[yj,1,yj,2],[zj,1,zj,2]},同时定义单元格j-1的坐标区间为{[xj-1,1,xj-1,2],[yj-1,1,yj-1,2],[zj-1,1,zj-1,2]}。
步骤2:判断A(x,y,z)与一级单元坐标区间的相对位置,若x∉[xj-1,1,xj-1,2]且y∈[yj-1,1,yj-1,2],z∈[zj-1,1,zj-1,2],则定义ox轴为二级单元格扩展方向,并且当x>xj-1,2时,则沿ox轴正方向扩展,反之沿负方向扩展。若存在2个或2个以上坐标超出单元格j-1的坐标区间,则任选一个方向作为扩展方向。
步骤3:以扩展方向为ox轴方向为例,以A点为几何中心,在平行于oyz的平面内作边长为Δy和Δz的长方形平面k1,各边分别与oy轴和oz轴平行。
步骤4:将步骤3中的长方形平面沿扩展方向平移Δx得到另一长方形平面k2(若k2平面超出一级单元,则直接取一级单元边界作为k2平面)。依次连接长方形平面的各个顶点kij(i=1,2;j=1,2,3,4),构成一个六面体单元。
步骤5:假设新待求点B的全局坐标为(xB,yB,zB),判断(xB,yB,zB)与当前二级单元坐标区间的相对位置。若在该二级单元内部,则以该二级单元节点进行插值计算;若不在该二级单元内部,按照步骤2确定点B所在二级单元的扩展方向,建立新的二级单元。以此类推,直至到达当前一级单元边界。
自适应二级单元在线生成示意图如图2所示,图中坐标点1~4对应顶点k11~k14,坐标点5~8 对应顶点k21~k24。
根据上述二级单元的构建方式,可确定以A(xA,yA,zA)为几何中心,沿ox方向构建二级单元时,对应的8个节点坐标依次为:
(2)
oy轴与oz轴的表达式可类推。
(a) 自适应二级单元沿坐标轴方向扩展示意图(a) Schematic diagram of second level adaptive grid extending on axis direction

(b) 自适应二级单元在线生成示意图(b) Schematic diagram of second level adaptive grid online building图2 二级单元构建示意图Fig.2 Schematic diagram of the second level grid structure
根据式(1),可将二级单元节点坐标转换为局部坐标(ξ,η,ζ),通过一级单元节点,采用基于反距离加权的广义延拓逼近算法,插值计算出二级单元各节点的扰动引力值,再通过拉格朗日插值法计算A点扰动引力值。
3 扰动引力赋值模型
3.1 基于反距离加权的广义延拓逼近算法
自适应网格插值计算的关键在于二级单元节点扰动引力的求解精度,但由于一级单元在构建过程中所选取的边长较长、网格较大,如果采用传统的拉格朗日插值方法必然导致计算结果存在较大误差,最终影响弹道扰动引力的计算精度。文献[7-9]将广义延拓逼近算法用于计算弹道扰动引力,得出结论:该算法的求解精度优于拉格朗日算法,并且广义延拓逼近算法求解精度随待求点位置的变化而变化,在每个单元边缘(靠近节点)的逼近结果优于单元中心(远离节点)。基于上述结论,本文在求解二级单元节点扰动引力的过程中,根据反距离加权插值算法,引入距离权系数矩阵,提出了一种优化广义延拓逼近算法。在计算过程中考虑待求点与已知节点的相对位置关系,进而提高二级单元节点扰动引力值的求解精度。
3.1.1 一般广义延拓逼近算法原理
根据延拓逼近的思想,六面体一级单元称为主域单元,将主域单元每个节点再分别沿x,y,z方向向外延伸,形成次域单元,如图3所示。每个主域单元有8个主节点,与之相连的次域单元有24个次域节点。
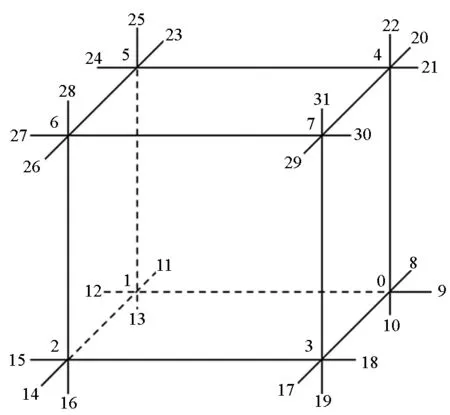
图3 一级单元延拓示意图Fig.3 Schematic diagram of the first level grid extension
由于扰动引力是坐标的函数,因此在一级单元内采用阶次为m的多项式来逼近待求点的扰动引力。根据文献[10],为了避免出现严重的龙格现象,增强多项式的容错性,选取m=17,并且设a为多项式系数向量,Fi为多项式类,即
a=[a0,a1,…,a16]T
(3)
(4)
因此逼近函数可以表示为:
δi=Fia
(5)
广域延拓逼近要求主域节点上的多项式值与扰动引力计算结果相等,而次域节点上的多项式值与扰动引力差值的平方和最小,即
(6)
其中,FI=[F1,F2,F3,…,F8]T,FJ=[F9,F10,F11,…,F32]T,s为主域与次域节点上的扰动引力值,sI=[s1,s2,…,s8],sJ=[s9,s10,…,s32]。
引入拉格朗日乘子λ=[λ1,λ2,…,λ8],可将模型表示为:
(7)
根据优化原理求解出a的值,通过式(5)结合待求点坐标即可求出该点的扰动引力值。
3.1.2 算法优化及求解
次域节点的作用在于将拟合的思想加入插值计算中,使得扰动引力插值结果与次域节点多项式值之差的平方和最小。但如果待求点位于网格边缘位置(靠近节点),则必然存在部分次域节点与待求点的距离较远,此时次域各个节点的重要程度应当有所区别。因此根据反距离加权插值思想,在次域节点拟合过程中引入距离权系数矩阵。
反距离加权插值算法是一种以距离作为权重的滑动平均加权插值法,其公式如下:
(8)
式中,f*表示待求点数值,f表示已知点数值,wi表示各已知点的权重。
(9)
式中,di为待求点与已知点之间的距离,k为幂指数。
根据式(9),建立次域节点与待求点的权系数对角矩阵:
(10)
结合式(7),优化广义延拓逼近算法的模型:
(11)
根据优化原理以及分块矩阵求逆,解出待定系数矩阵a。
(12)
式中,
(13)
结合式(5),扰动引力为:
(14)
结合2.2节中二级单元节点坐标的求解公式,即可求出二级单元各个节点的扰动引力值。
3.2 拉格朗日插值算法
在同等单元划分下,广义延拓逼近算法在精度上优于拉格朗日插值算法,但所需要的节点数目是拉格朗日插值算法的4倍。考虑到二级单元数量较多,如果同样采用广义延拓法计算二级单元内待求点扰动引力,必然会导致计算量加大。因此,在二级单元内部采用模型较为简单的拉格朗日插值算法求解。
假设二级单元内任意一点P的全局坐标为(x,y,z)(在求解过程中节点的全局坐标转换为局部坐标(ξ,η,ζ),为表述方便此处使用全局坐标(x,y,z)),根据2.2节可以求出二级单元各节点坐标(xm,ym,zm)(m=1,2,…,8)。采用形函数法求解P点扰动引力,令
N(x,y,z)=L(x)L(y)L(z)
(15)
式中,L(x),L(y),L(z)分别为计算x,y,z3个方向的拉格朗日插值基函数。以扩展方向为ox轴正方向为例,假设二级单元节点编号如图2所示,则8个节点对应的形函数分别为:
(16)
设二级单元节点处扰动引力为δm(m=1,2,…,8),则二级单元内一点P的扰动引力计算式为:
(17)
上述跳跃-滑翔弹道扰动引力赋值模型通过优化广义延拓逼近算法求解二级单元节点值,采用拉格朗日插值法计算自适应二级单元内部实际弹道点扰动引力值。在保证计算精度与计算速度的同时,可以减少弹上数据存储量,适合于弹上扰动引力的实时计算。
3.3 模型误差分析
由于在计算二级单元格节点数值时采用了最优平方逼近的拟合思想,因而无法推算其误差的解析表达式,因此本节采用仿真的方式对自适应网格赋值模型的误差进行分析说明。
根据插值算法截断误差公式可知,当待求点位置距离插值节点越近,则插值结果的误差越小,精度越高。因此所建立的赋值模型的误差分析思路为:
1)分析优化广义延拓逼近算法赋值精度与待求点位置的关系;
2)分析拉格朗日插值算法赋值精度与待求点位置的关系;
3)结合两种算法的误差变化曲线,分析本文赋值模型的误差变化曲线。
在分析算法赋值精度与待求点位置关系过程中,不同位置的待求点选取方法为:
1)在大地直角坐标系oexsyszs中的任意位置建立一个正六面体一级单元格,边长为L。
2)在一级单元格内部建立局部坐标系oxyz,原点o为单元格中心点,ox轴、oy轴及oz轴的指向与地心大地直角坐标系一致。
3)在局部坐标系内由原点出发,按照步长Δl向外扩展构建单元格,单元格边长记为li,新建单元格的顶点即为待求点,如图4所示。

图4 待求点选取示意图Fig.4 Schematic diagram of the point selection
由于三方向扰动引力的误差具有相似性,因此以zs轴方向扰动引力为例进行仿真计算。在仿真计算中取L=100 km,Δl=5 km,采用EGM2008模型计算一级单元节点扰动引力以及内部单元格节点扰动引力值,将同一单元格8个节点的标准误差值作为该距离下待求点的误差。
通过优化广义延拓逼近算法求解待求点扰动引力值,各内部单元格标准误差如表1、图5所示。

表1 优化广义延拓逼近算法不同位置待求点标准误差
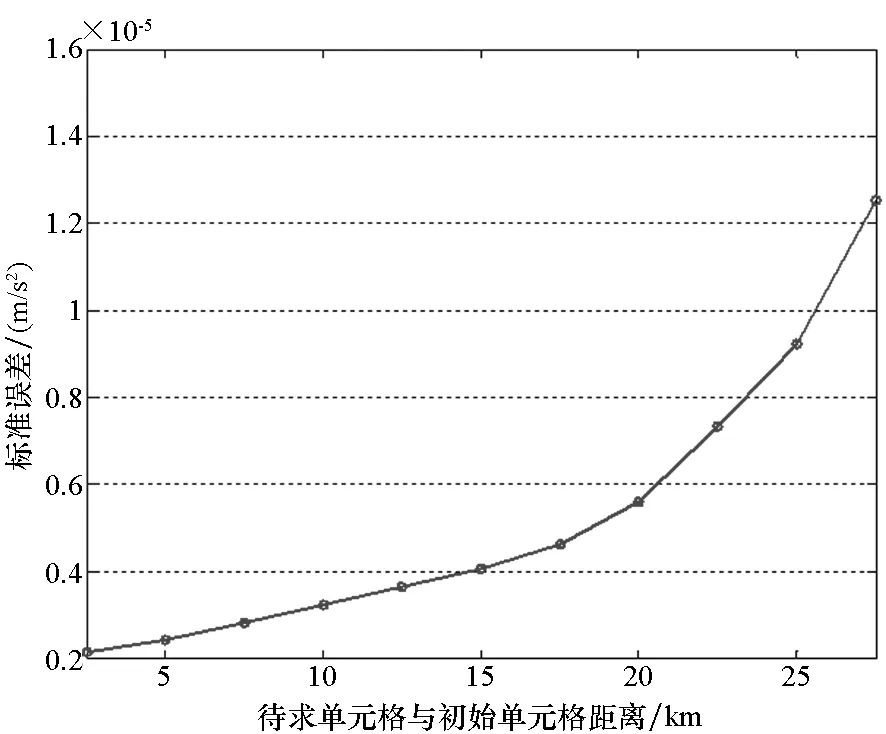
图5 优化广义延拓逼近标准误差与待求点位置关系Fig.5 Optimization generalized extension approximation standard error and point position
通过拉格朗日插值算法求解待求点扰动引力值,各内部单元格标准误差如表2、图6所示。
通过对两种算法误差曲线的分析,可以得出以下结论:
1)随着待求点与一级单元格节点距离的增加,其扰动引力值的求解精度逐渐降低,误差值逐渐增大。
2)随着距离的增大,误差的变化率逐渐增大。

表2 拉格朗日插值算法不同位置待求点标准误差
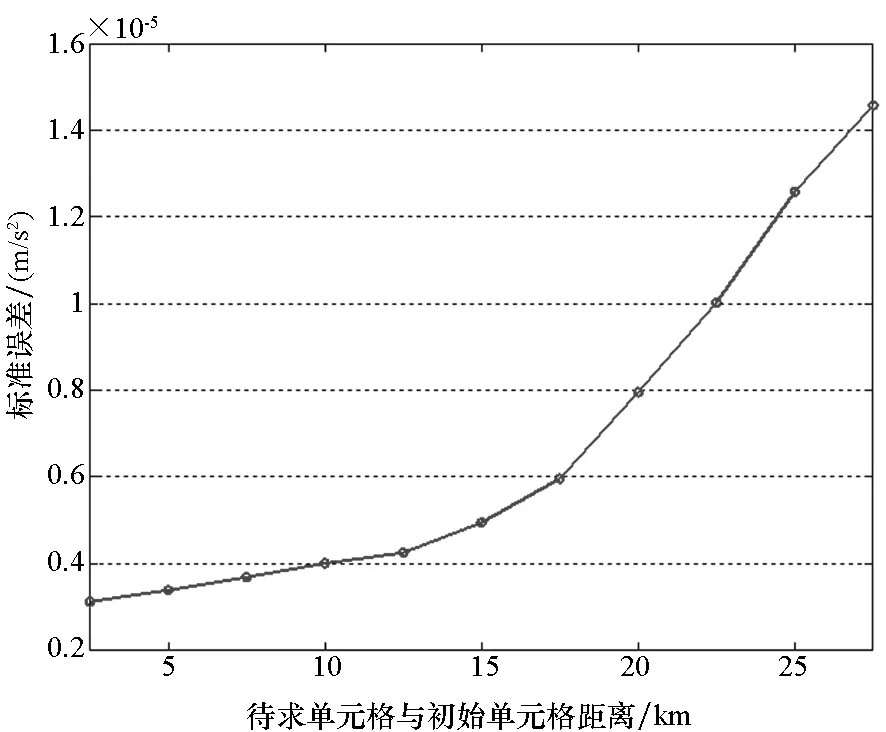
图6 拉格朗日插值标准误差与待求点位置关系Fig.6 Lagrange interpolation standard error and point position
本文的赋值模型采取了两级单元格分步逼近的方式,根据图5及图6两种算法的误差曲线可以近似采用如下公式表示:
(18)
其中:Δδi(i=1,2)表示两种算法的标准误差;ai,bi(i=1,2)表示两种算法误差的待定系数;xl表示待求点与其所在一级单元格最近节点的距离。
假设某一一级单元格I1内存在待求点A,其在一级单元格I1内对应的距离xl记为xA,因此当采用优化广义延拓逼近算法求解时,其标准误差为:
(19)
假设待求点A的拓展二级单元为I2,且单元格I2的中心点与一级单元格重合,此时二级单元格8节点在一级单元格I1内对应的距离xl相等,记为x1,待求点A在二级单元格I2内对应的距离xl记为x2。
当采用自适应网格赋值模型求解时,其标准误差为:
(20)
将式(19)与式(20)相减得:
(21)
式中由于误差计算采用的是标准误差,因此b2>0。当x1≥x2时,
(22)
由表1及表2可知,优化广义延拓逼近的误差小于拉格朗日逼近,结合图5及图6可知,a1-a2<0,且a1与a2的差距较小,因此3a1-a2>0,R>0,即自适应网格赋值模型的误差小于优化广义延拓逼近。
4 仿真分析
4.1 基本仿真条件
一级单元划分以参考弹道所在再入段坐标系空域为基础进行划分,一级单元以及自适应二级单元均划分为正六面体。一级单元节点扰动引力采用球谐函数法进行赋值,采用EGM2008模型2156阶位系数[11]。参考跳跃-滑翔弹道以远程高超声速滑翔式再入飞行器为对象,气动参数采用美国波音公司1998年设计的带控制翼的锥形体再入机动飞行器CAV-H的参数拟合得到[12]。
4.2 赋值精度分析
设定滑翔弹道的起始高度为70 km,起始速度为6500 m/s,为了使得仿真结果更具一般性,取步长为45°,将再入方位角由0°递增至315°,选此8个再入方位角的典型跳跃-滑翔弹道进行仿真计算[13],将8条弹道对应的误差结果取平均值作为最终结果进行精度分析。考虑到弹道末端扰动引力对落点精度影响很小,因此以高度20 km作为滑翔弹道终端条件,一级单元划分选择相邻节点间Δx=Δy=Δz=100 km,同时二级单元选定Δx=Δy=Δz=20 km。图7给出了正北方向弹道扰动引力逼近效果(由于篇幅有限,仅给出x轴方向逼近效果图),参考值为采用球谐函数法计算得到的扰动引力值,所采用的数据与节点赋值数据相同。图8给出了不同逼近方法标准差对比。表3给出了在同等单元格划分下,不同赋值方法对三方向扰动引力的逼近精度。

图7 扰动引力逼近效果图Fig.7 Accuracy of gravity anomaly approximating

图8 不同赋值方法标准误差对比Fig.8 Comparison of standard error of different assignment methods
通过分析上述图表的仿真结果可得:
1)由图7的逼近效果可以看出,所建模型的赋值精度较高,误差不随时间的增加而积累,整体逼近效果较好。
2)由图8可知,优化广义延拓逼近的标准误差小于传统广义延拓逼近,优化广义延拓自适应网格的标准误差小于广义延拓自适应网格,因此基于反距离加权的优化广义延拓算法进一步提高了传统广义延拓逼近算法的求解精度,有更好的逼近效果。
3)自适应网格插值与传统网格插值相比较,自适应网格的标准误差没有因为二次插值而增加,同时在加入优化广义延拓之后,其标准误差与传统广义延拓自适应网格相比有所下降,逼近精度提高。

表3 不同赋值方法逼近精度比较
考虑到扰动引力计算的主要目的是进行扰动引力落点影响修正,因此给出了优化广义延拓自适应网格的逼近误差对应落点偏差的大小,其横向偏差为1.225 4 m,纵向偏差为4.338 2 m[14]。
4.3 弹上存储量分析
弹上存储量的大小与单元格划分大小直接相关,在保证逼近精度的前提下,单元格划分越大,则所需要的单元格数量越少,因此弹上需要存储的数据量越少;反之,单元格划分越小,则所需单元格数量越多,从而弹上存储量越大。
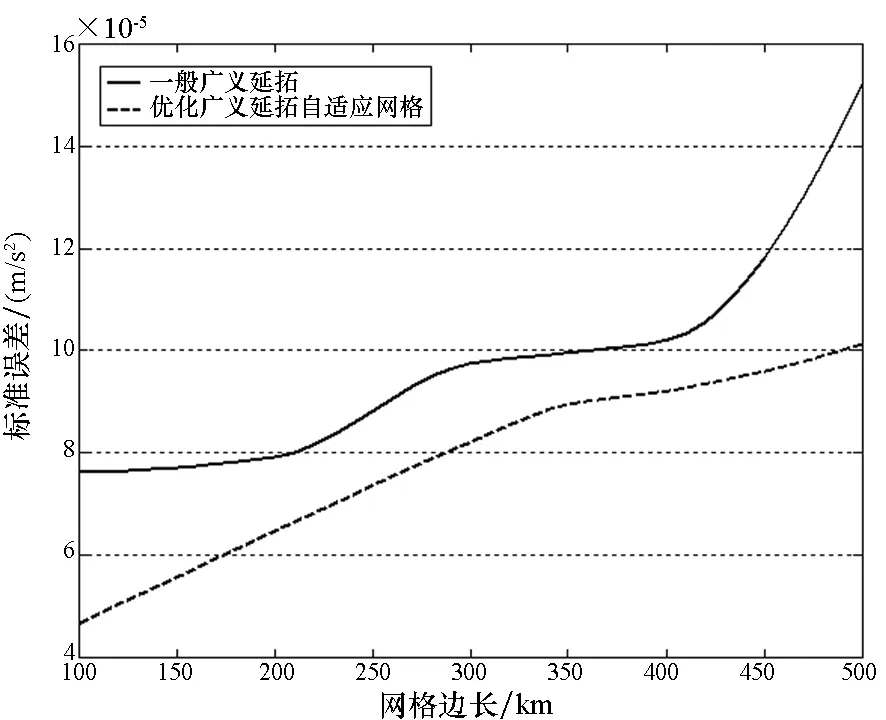
将网格划分为正六面体,边长取L,针对一般广义延拓逼近法和优化广义延拓自适应网格模型,通过选取不同的网格划分大小,分别分析两种赋值方法的逼近精度。表4为四种网格大小下赋值算法的绝对误差最大值以及标准误差。图9表示三方向标准误差随网格大小的变化情况,其中初始边长L0=100 km,步长ΔL=50 km,最大网格边长Lf=500 km。

表4 不同单元格大小下算法的逼近精度比较

(a) x
(b) y
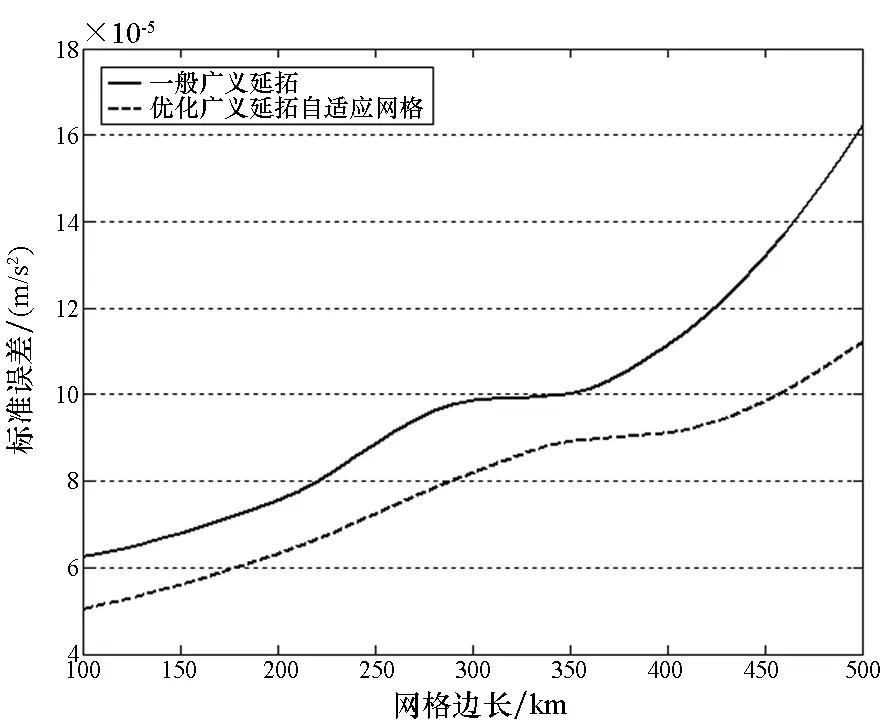
(c) z图9 标准误差随网格大小变化情况Fig.9 Variation of standard error with the size of the grid
由上述图表可知:
1)两种赋值方法的逼近误差随着网格边长的增加而增大,但自适应网格模型的标准误差的变化率总体上低于一般广义延拓逼近方法。
2)当标准误差相等时,自适应网格赋值方法对应的单元格边长较长,图9(c)中,当标准误差为10×10-5m/s2时,一般广义延拓的单元格边长约为325 km,而自适应网格赋值的单元格边长约为450 km,单元格边长增幅超过38%。因此在同等精度要求下,与一般赋值方法相比,优化广义延拓自适应网格赋值方法的最大网格边长更长,可以减少参考弹道的网格划分数量,从而减小弹上数据存储量。
4.4 适应性分析
自适应网格插值方法依赖于基准弹道,基准弹道的形状可能会影响单元的构建,进而对扰动引力赋值精度造成影响。因此有必要分析在不同滑翔距离、滑翔方向下自适应网格赋值方法的适应性。
通过改变起始速度,分别针对滑翔距离为9000 km、13 000 km以及16 000 km的三条跳跃滑翔弹道进行分析。图10表示起始滑翔方向为-180°~180°情况下三条弹道扰动引力逼近误差对应落点偏差的大小。

图10 不同滑翔距离弹道扰动引力逼近 误差对应落点偏差Fig.10 Drop point deviation corresponding to the gravity anomaly approximation error under different gliding distance
由图10可知,滑翔距离越远,扰动引力逼近误差对应落点偏差越大,但均保持在5 m之内。由此可知,在各个起始滑翔方向下,扰动引力逼近精度均很高,可以满足导弹精度要求,自适应网格模型具有较好的适应性。
4.5 赋值速度分析
扰动引力的赋值包括两个方面:地面数据准备阶段和弹上实时赋值阶段。在普通配置的微机上(CPU主频2.53 GHz,内存512 MB),对于4.2节的跳跃-滑翔弹道,地面数据准备时间为16.8 s,弹上单点赋值时间为0.19 ms。因此自适应网格模型虽然增加了计算量,但计算时间仍然满足快速诸元计算以及弹上实时计算需要。
5 结论
本文提出了一种自适应网格赋值模型,并根据反距离加权理论,优化了广义延拓逼近算法。通过与传统赋值方法的对比分析以及适应性分析,得出以下结论:
1)在同等大小的网格划分下,优化广义延拓自适应网格模型的逼近精度高于一般赋值方法。
2)随着单元格边长的增加,优化广义延拓自适应网格赋值模型的误差增加平缓,在同等精度要求下,该赋值模型的最大单元格边长大于一般赋值方法,从而减小了单元格划分数量,降低了弹上数据存储量。
3)该赋值模型能够适应不同滑翔方向以及不同滑翔距离的弹道扰动引力快速赋值,逼近误差对应落点偏差小于5 m。同时模型的计算速度满足快速诸元计算以及弹上实时计算需要。
