内压作用下复合材料修复裂纹管道的失效分析*

邱金水，陈如木，刘伯运，任广鲁

(海军工程大学 动力工程学院， 湖北 武汉 430033)

舰船和海洋平台管道在制造、安装、服役过程中，以及在潮湿、湿热等恶劣环境中极易使管道产生裂纹缺陷，在管道内部介质高压作用下可能会使裂纹缺陷发生失稳扩展，并且足以在压力管道运行期间引起灾难性的结构失效[1-2]。因此，应定期对管道进行裂纹缺陷检测，并及时对管道含裂纹区域进行结构增强修复，以确保其安全性及结构完整性。

纤维增强聚合物复合材料(Fiber Reinforced Polymer, FRP)越来越多地应用于缺陷构件(管道表面金属损伤缺陷、管道表面裂纹及钢板裂纹)的加固及修复[3-7]。利用这些复合材料来修复含缺陷的管道比传统修复技术具有独特的优势，不仅消除焊接造成的爆炸危险，而且由于FRP的质量较轻而使得复合材料修复系统易于安装操作，较高的比强度/模量使较薄的复合材料加固层即可增强裂纹结构[8]。

FRP加固陆上和海上缺陷管道的方法正在迅速发展，其性能、设计方法及潜在的应用范围均应进行深入的研究。目前，大多数文献较深入地研究了复合材料修复局部腐蚀管道的修复性能及极限承压能力[9-11]，而对于复合材料修复含裂纹管道的研究较少。且现有文献对于修复裂纹的有效性均通过在一定内压作用下修复前后管道裂纹尖端应力强度因子的降低程度来表征[12-13]，虽然该方法在一定程度上可以验证复合材料修复含裂纹管道的有效性，但其并未考虑在内压作用下裂纹管道修复后的极限承载能力，即在其所建立的数值模型中并未考虑管道的裂纹扩展、胶层的脱粘失效以及复合材料层的失效。文献[14]研究了玻璃纤维增强聚合物复合材料修补受内压作用的裂纹钢管的修复性能，以及纤维取向对减小裂纹前沿J积分的影响。虽其所提数值模型考虑了钢材料的塑性行为，但该数值模型假定复合材料贴片与管道外表面之间的界面为绑定约束，并未将胶层考虑在内，因此，其数值计算结果具有一定的偏差。

针对上述存在问题，为了准确评估在极限内压作用下FRP修复含裂纹管道的有效性、失效压力以及管道裂纹扩展行为，本文利用ABAQUS有限元软件建立复合材料修复后裂纹管道的失效数值模型。

1 扩展有限元法

研究结构裂纹扩展的方法中，具有代表性、可靠的数值方法有经典有限元方法和扩展有限元方法(eXtended Finite Element Method, XFEM)，每种方法都有其自身的优点，可用于特定类型的问题。在经典的有限元方法中，结构应该以裂纹体与单元边界重合的方式进行网格划分，即裂纹扩展只能沿着单元边界进行，无法做到沿任意路径扩展[15]。因此对于研究裂纹扩展行为的问题，应该考虑裂纹的预定义路径，或者对于任意的裂纹扩展问题，裂纹扩展的每一步后都应该重新生成及细化网格。

XFEM可弥补经典有限元方法的不足，该方法不需要重新细化网格，并且在含裂纹的结构区域可使用规则的网格进行划分，不需要将裂纹边界与单元边缘匹配重合。扩展有限元的核心思想是在传统有限元位移自由度的基础上扩充两项，分别引入间断跳跃函数和裂纹尖端渐进函数。其中：间断函数用于描述裂纹面穿过单元内的位移跳跃；裂纹尖端渐进函数则用来模拟裂纹尖端附近的应力奇异性。而ABAQUS提出一种思路，如若裂纹每一次扩展需要通过一个完整单元，表示裂纹尖端的渐进函数可以省略，因此裂纹穿越区域内的位移方程可以表示为：

(1)

式中：Nl(x)是节点形函数；ul是传统意义上的标准节点位移向量，它作用于模型内的所有单元上的节点；H(x)为间断跳跃函数，al为其对应的扩充自由度，H(x)al作用于模型内被裂纹面切开的单元上的节点。

间断跳跃函数可以表示为：

(2)

式中,x为单元的Gauss积分点,x*是裂纹上最接近x的点，n是裂纹在x*上的外法线向量。

2 材料模型

2.1 钢材料模型

管道钢材料是20号钢，其为各向同性材料，且考虑了弹塑性行为。在MTS型万能实验机上对20号钢标准试件进行拉伸试验，可得材料的杨氏模量、屈服强度和泊松比分别为206 GPa、305 MPa和0.3，钢材料的塑性行为通过真实应力-塑性应变曲线来定义，如图1所示。

图1 20号钢真实应力-塑性应变曲线Fig.1 True stress versus plastic strain of Steel 20

在利用XFEM进行管道裂纹扩展模拟时，需确定钢材料的失效机理，包括损伤初始准则和损伤演化规律。选取最大主应力作为钢材料发生损伤的起始判据，该参数主要影响材料初始损伤的最大承载能力。而损伤演化规律与内聚力理论类似，主要基于牵引-分离本构行为，即需预先设置等效临界能量释放率Gc，该参数主要影响材料损伤后抵抗裂纹扩展的能力。这两个参数的取值大小会直接影响XFEM模拟裂纹的准确性。本文参考文献[16]中的方法，通过含裂纹试件的拉伸试验及其所对应的数值模型，对试验及数值模型得到的载荷-变形响应进行对比分析，从而确定最大主应力及能量释放率的临界值分别为380 MPa和120 N/mm。

2.2 胶层材料模型

管道外表面与复合材料缠绕层之间的界面采用胶层连接，在数值分析模型中采用cohesive单元模拟胶层的脱粘失效，该单元本构模型所定义的力-位移关系(牵引-分离曲线)包括单元损伤前的线弹性阶段和损伤后的刚度退化阶段[17]，如图2所示。当所施加的载荷达到临界点时，界面单元刚度按照损伤演化准则开始逐渐退化，随着单元中损伤参数的增加，机械性能会降低到单元发生完全损伤时失效，从而可以模拟胶层的损伤和脱粘。cohesive单元的初始损伤采用最大应力失效准则，研究所采用的胶层材料性能见表1。

图2 胶层的双线性本构模型Fig.2 Bilinear constitutive model of adhesive layer

2.3 复合材料模型

由于管道修复用纤维复合材料是由玻璃纤维方格布经环氧树脂黏结形成的层合薄壳结构。对于层合薄壳结构的失效，可暂不考虑其层间及细观结构的失效，视层合薄壳为各向异性材料，并将其宏观力学性能使用复合材料工程常数进行描述，纤维复合材料的工程常数和损伤强度阈值均由层合板试验测定[18]，如表2所示。采用ABAQUS有限元软件中的最大应力失效准则进行失效模拟。最大应力失效准则是最常用的限制性失效准则，即对应力设置最大限制值，当至少一个应力分量(沿材料主轴)超过该方向的极限强度时，FRP层合板失效。最大应力失效准则能够很好地表征非延性材料的失效行为，其表达式为：

(3)

式中，σ11为复合材料纵向应力，σ22为横向应力，σ12为12向切向应力，X为纵向强度，Y为横向强度，S为切向强度。

表1 胶膜参数

3 复合材料修复裂纹管道的失效数值模型

图3为FRP修复裂纹管道的几何模型，主要包括裂纹管道、胶层、复合材料缠绕层、初始裂纹。其中，管道外直径D为108 mm，管道壁厚t为4 mm。在管道外表面设置轴向初始裂纹，并将其形状简化为规则的半椭圆形状[13-14]，通过选取管道裂纹半长a、裂纹深度d、玻璃纤维布缠绕层数e来表征不同的修复工况(a,d,e)。修复层的轴向长度参考ASME PC-2-2015中的规定，由式(4)确定。

(4)

式中,L是复合材料修复层的轴向长度。

表2 玻璃纤维布增强环氧树脂基复合材料层合板性能参数

1—含裂纹管道；2—初始裂纹；3—复合材料缠绕层；4—胶层图3 复合材料修复裂纹管道数值模型Fig.3 Numerical model of cracked pipelines repaired by composites

为了减小边界效应的影响，数值模型中管道长度须取管道直径的3～5倍，取全尺寸数值模型长度为800 mm。对几何模型的左右两端施加全约束，同时为避免管道端部应力集中的影响，在距离左右端部40 mm处对裂纹管道模型进行切割，仅对40～760 mm处的管道内表面施加单调递增的内部压力，如图3所示。为了避免各层之间相互作用而导致的数值模拟错误，各层之间接触面施加绑定约束。

管道结构采用C3D8R 三维实体单元进行网格划分。XFEM虽能有效减少裂纹扩展时的网格敏感性，但是仍然无法完全消除网格密度的影响，过低的网格密度仍然会带来不准确的计算结果[17]。因此，需基于收敛性选择网格单元的最佳数值，即网格单元数设置对含裂纹管道失效压力的影响。经模拟计算，超过以下网格划分方法设置的单元数，裂纹管道的失效压力值趋于稳定值。网格划分方法为：对管道初始裂纹周围及可能扩展的区域进行网格加密处理，如图4所示，加密区域轴向长度为100 mm,在其轴向上布置50个单元，在其左右两侧的非加密区域的轴向上分别布置40个单元，在管道的环向上布置61个单元，奇数是为了保证初始裂纹位于网格内部，而不在网格的边界上，否则会影响裂纹扩展的准确性；胶层采用cohesive单元进行网格划分，其在厚度方向只能划分1层网格，网格控制属性必须采用扫掠技术，同时扫掠方向必须为单元厚度方向；复合材料缠绕层采用SC8R连续壳单元进行网格划分，同样其扫掠方向也须为缠绕层厚度方向；胶层和复合材料缠绕层在轴向及环向长度上布置的单元数与管道一致。

图4 裂纹区域网格细化Fig.4 Mesh refinement of crack area

而后使用静力通用分析步骤求解该数值模型，管道内部压力随分析时间单调递增，直至管道真实裂纹贯穿整个壁厚，或者胶层发生脱粘失效，或者复合材料修复系统失效(判定依据为复合材料缠绕层中应力值达到最大应力失效准则，即复合材料修复裂纹管道的任一组件达到各自的失效准则)。

4 静水压爆裂试验

为验证复合材料修复裂纹管道的失效数值模型的有效性及预测结果的准确性，对含裂纹管道及修复后的裂纹管道进行静水压爆裂试验。图5为静水压爆裂试验装置，主要包括高压液压泵、裂纹钢管、压力传感器、压力记录仪等。钢管试件是由20号钢制成的，其尺寸与数值模型尺寸一致，利用高压液压泵对复合材料修复前后含裂纹钢管试件进行注水加压，直至钢管试件发生爆裂失效，利用压力记录仪记录钢管试件爆裂失效时所对应的压力值。

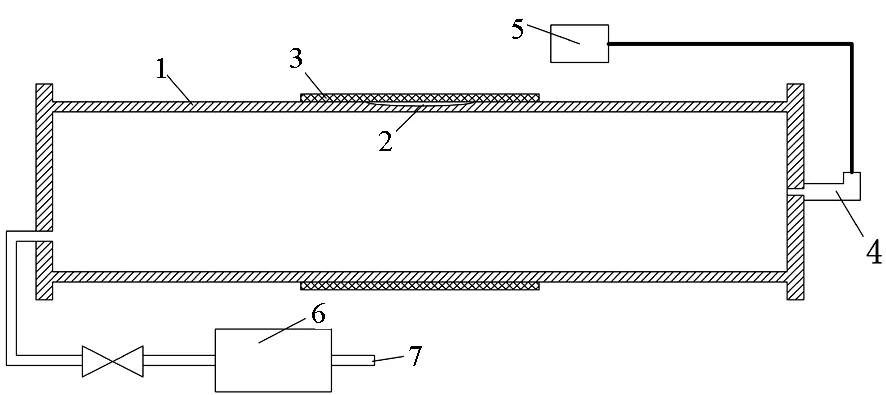
1—裂纹钢管；2—裂纹缺陷；3—修复层；4—压力传感器； 5—压力记录仪；6—高压液压泵；7—水源图5 静水压爆裂试验装置Fig.5 Hydrostatic burst test device

5 结果与讨论

5.1 数值计算与试验结果对比

利用静水压爆裂试验装置分别对试件1、试件2进行爆裂压力加载试验，其中，试件1为含裂纹钢管试件，预制缝隙尺寸(a,d)为(25 mm，3 mm)，试件2为在裂纹钢管(对应于试件1)的外表面缠绕的复合材料。

表3为试件1、试件2的实验结果与相对应的数值计算结果对比。由表3可知，裂纹钢管试件的实验值大于其所对应的模拟值，两者之间的差异为8%，其原因可能为所使用的钢管试件中的裂纹是通过切割而成的裂缝进行表征的，相同尺寸的裂缝与裂纹相比具有较大的承载能力，同时钢管尺寸、裂缝尺寸的加工精度以及数值模拟过程中边界条件的简化均会使实验与结果之间产生一定的差异；而复合材料修复后的裂纹钢管试件的实验值小于其所对应的模拟值，两者之间的差异为2.7%，其原因可能为在数值模型中复合材料缠绕层为理想状态，无任何缺陷，但在实际缠绕裂纹钢管中，复合材料缠绕层成型后会存在各种缺陷，并不能达到数值模型中的理想状态。

表3 数值计算与试验结果对比

复合材料修复裂纹钢管试件的静水压爆裂试验值与模拟值虽存在一些差异，但其在一定程度上验证了失效数值模型的预测结果。静水压爆裂试验仅能得到极限爆裂失效压力值，而对于在加压过程中管道裂纹的扩展、胶层的脱粘失效以及复合材料的失效只能通过失效数值模型进行研究。

5.2 裂纹管道的爆裂失效分析

图6为含初始裂纹(25 mm，3 mm)的管道在爆破过程(内部压力增大过程)中管道外表面的应力分布情况。由图6可知，随着内部压力载荷的逐步增大，管道应力集中于裂纹尖端区域，而在初始裂纹的两侧形成了低应力区域，说明该区域失去了抵抗内压载荷的能力。

STATUSXFEM值为XFEM单元的状态值，若该值在0～1范围内，说明在此单元处形成黏结裂纹，若该值等于1，则在此单元处形成真实裂纹。因此，含裂纹管道的失效通过管道内壁单元的STATUSXFEM值进行判定。若出现STATUSXFEM值为1的内壁单元，则认为裂纹贯穿整个壁厚，含裂纹管道发生爆裂失效。

图7为含初始裂纹(25 mm，3 mm)的管道在爆破失效过程(内部压力增大过程)中内表面的应力分布及裂纹扩展情况。图7(a)、图7(c)为内压增大至22.35 MPa时，内表面的应力分布及裂纹扩展情况；图7(b)、图7(d)为内压增大至22.36 MPa时，内表面的应力分布及裂纹扩展情况。由图7可知：随着管道内部压力不断增加，初始裂纹沿深度方向逐渐扩展至管道内表面，当内压上升至22.35 MPa时，管道内壁单元形成黏结裂纹，这说明此时内壁单元处裂纹尖端的最大主应力值达到钢材料发生损伤的起始判据，但此时管道仍具有抵抗内部压力的能力。随着内部压力进一步增大至22.36 MPa时，内壁单元处裂纹尖端的能量释放率达到裂纹阻力率，裂尖处的黏结裂纹开始扩展成真实裂纹，裂尖单元的STATUSXFEM值达到1，裂纹沿轴向方向失稳扩展，真实裂纹贯穿管道整个壁厚方向，即认定管道发生爆裂失效，此时所对应的管道内部压力即为含初始裂纹(25 mm，3 mm)管道的极限承压能力(失效压力)。含初始裂纹(25 mm，1 mm)、(25 mm，2 mm)管道的爆裂失效压力分别为28.88 MPa、24.77 MPa，说明初始裂纹深度对裂纹管道的失效压力具有较大的影响。

(a) 22.35 MPa

(b) 22.36 MPa图6 爆破失效过程管道外表面的应力分布Fig.6 Stress distribution on the outer surface of pipeline during blasting failure

图8为含裂纹管道的爆裂失效压力随轴向裂纹半长的变化曲线，取裂纹深度为2 mm。由图8可知，裂纹管道爆裂失效压力在裂纹轴向半长为10～20 mm范围内迅速下降，当l≥20 mm时，爆裂失效压力趋于稳定值，即不再随着裂纹轴向半长的变化而变化。对所获得的压力Pf数据进行指数拟合，得到拟合函数为Pf=13×exp(a/5.5)+24.6。同时根据拟合的决定系数R2来判断拟合结果的优劣，该拟合曲线的决定系数R2=0.988，R2接近于1，表明拟合效果好，同时也说明爆裂失效压力Pf随初始裂纹半长呈指数形式下降。

(a) 22.35 MPa时应力分布(a) Stress distribution under 22.35 MPa

(b) 22.36 MPa时应力分布(b) Stress distribution under 22.36 MPa

(c) 22.35 MPa时裂纹扩展(c) Crack propagation under 22.35 MPa

(d) 22.36 MPa时裂纹扩展(d) Crack propagation under 22.36 MPa图7 爆破失效过程管道内壁的应力分布及裂纹扩展Fig.7 Stress distribution and crack propagation of inner wall during blasting failure

图8 含裂纹管道爆裂失效压力随裂纹半长的变化趋势Fig.8 Trend of failure pressure of cracked pipelines with half length of crack

4.3 修复后裂纹管道的失效分析

研究修复层厚度(玻璃纤维复合材料层数)对修复性能的影响，对不同的复合材料缠绕层数修复同一管道裂纹工况进行失效模拟。由分析结果可观察到不同修复工况呈现相同的失效模式，即管道内表面首先出现黏结裂纹，而后复合材料内层应力急剧上升到极限强度后失效。下面以修复工况(25 mm，3 mm，6 mm)为例对失效模式进行详细分析。

在ABAQUS软件的后处理中，纤维增强树脂复合材料的最大应力失效准则通过MSTRS值进行表征：当MSTRS值小于1时，说明复合材料处于弹性阶段；当MSTRS值大于等于1时，说明该单元的应力分量超过了纵向或横向方向的极限强度，认为复合材料缠绕层失效。胶层的失效判定通过cohesive单元的损伤参数SDEG值进行表征：当出现单元的SDEG值大于0时，说明该单元达到损伤起始判据——最大应力失效准则，其刚度开始退化；当SDEG值等于1时，说明该单元的刚度完全退化并失效。

图9为复合材料修复裂纹管道数值模型中裂纹管道内壁、复合材料缠绕内层、复合材料缠绕外层、胶层的失效判定云图。当内部压力载荷上升至26.376 MPa时，黏结裂纹在管道内壁单元生成。同时，复合材料缠绕内外层的应力主要集中于管道裂纹区域上方。其主要原因是：在不断增大的内压载荷作用下，管道初始裂纹具有向两侧张开的趋势，而复合材料层的存在能够很好地抑制裂纹张开趋势，进而裂纹区域将载荷传递至其上方的复合材料区域。此时，复合材料缠绕内层的MSTRS最大值为0.322，复合材料缠绕外层的MSTRS最大值为0.182，可判定复合材料层的最大应力分量并未超过材料主轴方向的极限强度；胶层的最大SDEG值为0.813，说明胶层中已有单元发生刚度退化，但仍具有一定的承载能力，因此在26.376 MPa内部压力载荷作用下，复合材料修复裂纹管道并未完全失效。

(a) 26.376 MPa时裂纹管道内壁 (b) 26.391 MPa时裂纹管道内壁(a) Cracked pipe wall under 26.376 MPa (b) Cracked pipe wall under 26.391 MPa

(c) 26.376 MPa时复合材料缠绕内层 (d) 26.391 MPa时复合材料缠绕内层(c) Twined internal layer of composite material under 26.376 MPa (d) Twined internal layer of composite material under 26.391 MPa

(e) 26.376 MPa时复合材料缠绕外层 (f) 26.391 MPa时复合材料缠绕外层(e) Twined outer layer of composite material under 26.376 MPa (f) Twined outer layer of composite material under 26.391 MPa

(g) 26.376 MPa时胶层(g) Adhesive layer under 26.376 MPa (h) 26.391 MPa时胶层(h) Adhesive layer under 26.391 MPa图9 失效数值模型中各组件的失效判定Fig.9 Failure judgment of each component in failure numerical model

随着内部压力进一步上升至26.391 MPa，管道内壁单元的黏结裂纹沿轴向扩展，且此时内壁单元的STATUSXFEM值并未增大至1，说明在管道内壁面未形成真实裂纹。同时，由于管道内壁面单元形成黏结裂纹，其承载力急剧下降，其外表面裂纹张开趋势急剧上升，进而使得复合材料内外层的应力和MSTRS最大值急速上升，复合材料内层的MSTRS最大值上升至1.056，复合材料外层的MSTRS最大值上升至0.497，内层的MSTRS最大值已超过1，表明该层的最大应力分量超过了材料在该方向的极限强度，即可判定复合材料缠绕层失效；但此时胶层的最大SDEG值上升至0.838，表明胶层未完全失效。因此，在26.391 MPa内压作用下，复合材料修复裂纹管道中的复合材料缠绕层失效，复合材料修复系统中任一组件发生失效，即判定修复系统失效，此时所对应的管道内部压力即为该修复工况下的极限承载能力(失效压力)。

图10为复合材料修复后含裂纹管道的失效压力随复合材料缠绕层数的变化趋势，其中取裂纹工况为(25 mm，2 mm)和(25 mm，3 mm)。由图10可知，在复合材料修复工况(25 mm，3 mm)中，当复合材料缠绕层数小于6时，复合材料修复系统的失效压力随着缠绕层数而呈近似线性增长；而当缠绕层数大于6时，失效压力的增量可忽略不计。因此，从复合材料修复效能及经济性角度考虑，可选择缠绕6层复合材料作为裂纹工况(25 mm，3 mm)的临界缠绕层数，与未修复裂纹管道的爆裂失效压力(22.36 MPa)相比，缠绕6层修复后失效压力提升了18%，验证了复合材料修复系统的有效性。而对于修复工况(25 mm，2 mm)而言，其临界缠绕层数为8，且失效压力提升了21.7%。由图10亦可知，与对裂纹管道失效压力的影响类似，初始裂纹深度对复合材料修复后的裂纹管道的失效压力亦具有较大程度的影响。

图10 失效压力随复合材料缠绕层数的变化趋势Fig.10 Failure pressure changes with the number of layers of composite materials

图11为裂纹管道在缠绕6层复合材料前后的失效压力随裂纹轴向长度的变化趋势，对修复工况(3 mm，0)、(3 mm，6)所获得的失效压力Pf数据进行指数拟合，两拟合曲线的决定系数分别为0.972和0.984，表明拟合效果好，同时也说明复合材料修复裂纹管道后的失效压力亦随着裂纹轴向长度的增大而呈指数形式下降。同时，由图11亦可知，在不同裂纹轴向长度下，修复后裂纹管道失效压力的增量基本相等。

图11 失效压力随裂纹长度的变化趋势Fig.11 Failure pressure changes with crack length

6 结论

本文提出了包含裂纹管道、胶层、复合材料缠绕层的失效数值模型，以裂纹深度、裂纹轴向长度以及复合材料缠绕层数来表征不同的修复工况，对不同的裂纹修复工况进行非线性数值分析，根据分析结果可知：

1)未修复裂纹管道在单调递增的内部压力作用下，初始裂纹沿轴向及壁厚方向逐渐扩展，进而使得管道内壁单元形成黏结裂纹。随着载荷的进一步增加，黏结裂纹处扩展成真实裂纹，此时真实裂纹贯穿整个壁厚方向，即认定裂纹管道发生爆裂失效。初始裂纹尺寸对裂纹管道的失效压力具有较大影响，爆裂失效压力随初始裂纹半长呈指数形式下降。

2)由数值分析结果可知，不同修复工况呈现相同的失效模式。在管道单调递增的内部压力作用下，管道内表面首先出现黏结裂纹，其外表面裂纹张开趋势急剧上升，使得复合材料内层应力急剧增大，达到极限强度而发生失效，此时所对应的内部压力即为修复后裂纹管道失效压力。对于不同的初始裂纹尺寸存在对应的复合材料缠绕层数临界值，且修复后失效压力亦随着裂纹轴向长度的增大而呈指数形式下降。