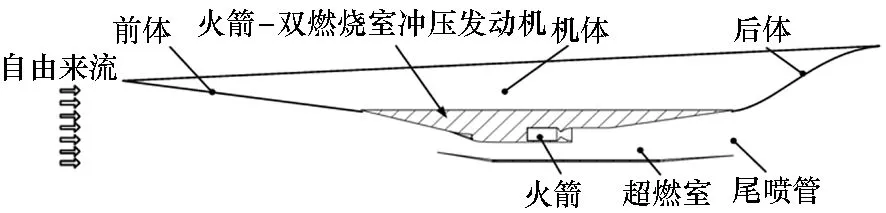
火箭-双燃烧室冲压组合循环发动机概念研究*

2019-10-14吴继平谭建国张紫豪

国防科技大学学报 2019年5期

吴继平，谭建国，陈健，张紫豪

(1. 国防科技大学空天科学学院，湖南长沙 410073；2. 国防科技大学高超声速冲压发动机技术重点实验室，湖南长沙 410073)

临近空间是地球大气层内海拔高度20 km到100 km之间的区域[1-2]。这个区域在军事侦察和商业通信上具有重要意义。高超声速飞行器非常适合在临近空间飞行，近年来获得了广泛关注[3-7]。

在高超声速飞行条件下，超燃冲压发动机具有非常高的性能，世界范围内开展了大量研究。然而，超燃冲压发动机难以自启动。为了解决该问题，组合循环发动机的研究被提上日程。研究人员已经提出了好几种组合循环发动机方案[8-9]，并开展大量研究。其中火箭基组合循环(Rocket-Based Combined Cycle, RBCC)发动机就是最为人所熟知的一种方案。RBCC包含了引射模态、亚燃冲压模态、超燃冲压模态和纯火箭模态。然而，RBCC在超燃冲压模态时仍然存在一些问题：如关闭火箭，采用纯超燃模态，则由于煤油在超声速气流中燃烧困难，点火和火焰稳定面临巨大挑战[10-12]；若采用火箭以低工况作为火炬工作，可以解决点火与火焰稳定的难题，但推进剂比冲效率很低[13]。

20世纪80年代约翰霍普金斯大学的Billig等第一次提出了双燃烧室的概念[14]。双燃烧室将亚燃冲压发动机和超燃冲压发动机进行了最好的组合，在宽马赫数工作范围(3.5～6.5)内具有易点火、火焰稳定性强、低马赫数条件下性能高和壁面冷却方便等优点，但是在飞行马赫数超过6.5以后会变差。

在飞行马赫数不超过6.5的范围内，将火箭发动机和双燃烧室冲压发动机组合在一起具有非常广阔的前景。本文研究的临近空间飞行器如图1所示。该飞行器由多模块并联的火箭-双燃烧室冲压组合循环(Rocket Dual Combustion Ramjet Combined-cycle, RDCRC)发动机作为动力。采用发动机与机体一体化设计，前体作为进气道的预压缩面，后体作为喷管的一部分。

图1 基于RDCRC发动机的临近空间飞行器示意Fig.1 Schematic of a near space vehicle with multi-module RDCRC engine

1 RDCRC发动机概念

RDCRC发动机由进气道、引射火箭、预燃室、超燃室和喷管组成，如图2所示。进气道分为超声速进气道和亚声速进气道。在一个RDCRC发动机模块中，包含了2个引射火箭、4个预燃室和1个超燃室。

图2 RDCRC发动机组成示意Fig.2 Schematic of RDCRC combined-cycle engine module

RDCRC发动机剖面示意如图3所示，其工作模态包含引射模态、引射亚燃模态、双燃烧室亚燃模态和双燃烧室超燃模态。

(a) 沿火箭对称面剖切(a) Section along the symmetry plane of the rocket

(b) 沿预燃室对称面剖切(b) Section along the symmetry plane of the preburner图3 RDCRC发动机剖面示意Fig.3 Schematic sections of RDCRC engine module

在引射模态，空气在引射火箭的引射作用下进入进气道，在混合段与引射火箭产生的高温燃气进行混合、引射增强、燃烧，并最终排出喷管，产生推力。

在引射亚燃模态，引射火箭工作类似于一个燃气发生器，可以工作在较高工况以产生加大推力，或者工作在较低工况以获得较高比冲效率。

在双燃烧室亚燃模态和双燃烧室超燃模态下，引射火箭关闭，预燃室作为火焰稳定装置提供连续、可靠的点火，发动机的比冲由于没有额外消耗氧化剂，从而可以获得更高的比冲。

当飞行马赫数小于3时，RDCRC发动机可以工作在引射模态；当飞行马赫数在2～5.5时，发动机可以工作在引射亚燃模态或双燃烧室亚燃模态；当飞行马赫数在5.5～6+时，发动机可以工作在双燃烧室超燃模态。

在飞行马赫数2～6之间可根据飞行任务的多学科优化来确定究竟选择使用高推重比、较低推进剂比冲效率的引射亚燃模态，还是较低推重比、高推进剂比冲效率的双燃烧室亚燃模态。

2 弹道设计

2.1 空中发射弹道

基于RDCRC发动机的临近空间飞行器飞行弹道如图4所示。和X-43A类似[15]，由载机将飞行器运送到海平面10 km左右的高空，然后投放。在重力和RDCRC发动机的共同作用下，飞行器沿斜向下并最终转平的弹道加速至2马赫左右，飞行高度降至5～8 km，发动机工作在引射模态。之后依靠引射亚燃模态较高的推力增强性能和高动压带来的大升力加速爬升至3马赫(10～12 km)。然后，根据任务特性，采用弹道优化技术选择引射亚燃模态或双燃烧室亚燃模态进一步加速爬升至6马赫(26～30 km)，转入双燃烧室超燃模态进行巡航飞行。最后，在到达目标点后，临近空间飞行器滑翔返回并在RDCRC发动机的辅助下实现水平着陆，此时RDCRC发动机工作在引射模态。

图4 临近空间飞行器弹道示意Fig.4 Sketch trajectory of the air launched near space vehicle

2.2 推力计算模型

发动机性能分析参考位置如图 5所示，飞行器前体能够实现进气压缩的作用，后体主要由喉道构成。整个发动机位于临近飞行器的下部位置。

(a) 沿引射火箭对称面剖切(a) Section along the symmetry plane of the rocket

(b) 沿预燃室出口纵向对称面剖切(b) Section along the symmetry plane of the preburner图5 发动机参考位置示意Fig.5 Simplified engine reference stations

2.2.1 进气道

(1)

其中，

(2)

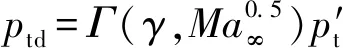
2.2.2 引射模型

在引射模态，预燃室入口关闭，引射火箭燃气作为一次流，进气道吸入的空气作为被引射的二次流。主火箭燃气与吸入的空气掺混，进行动量和能量的交换。

一般认为即时混合燃烧(Simultaneous Mixing and Combustion, SMC)模式的燃烧效率低于扩散后燃烧(Diffusion and AfterBurning, DAB)模式，因此本文采用DAB模式进行建模分析。基于此，假定引射火箭推进剂完全燃烧，在与来流空气混合过程中不存在任何燃烧。

假定主火箭喉道壅塞面积为A*，超声速一次来流与亚声速二次来流在等截面段进行引射混合。采用动量守恒、能量守恒和连续性方程求解等截面管道混合模型。同时假定：来流为无摩擦、稳态、绝热等熵；忽略进气压缩、一次流与二次流掺混和相互作用过程中以及热传递和火焰稳定过程中的压力损失；一次流与二次流在混合室入口处压力和速度分布均匀；在混合室内不发生化学反应，在混合室出口处完全混合均匀。

由此，给定飞行条件和推进剂组合，假定在虚拟的2′处p2′s=p2′p，则3处的气流参数由以下参数决定：

1) 引射火箭混合比ψ：该参数决定了一次来流的主要参数，如比热比γp、气体常数Rp、一次流总温比Θ=Tts/Ttp，定压比热容之比c=Cps-Cpp。

3) 二次流速度系数λs：该参数可以确定总压pts和静压ps。

给定推进剂组合，采用吉布斯自由能最小化方法，由引射火箭混合比ψ能够确定一次流参数(Ttp、γp和λp)。由此，可以得到引射系数n：

(3)

式中，

(4)

(5)

通过能量守恒方程和连续性方程，解出混合参数：

(6)

(7)

(8)

联立动量守恒方程和连续性方程，得：

(9)

式中，

(10)

|Z|>2时，可以解出实根λ3。负号对应λ3<1，正号对应λ3>1。亚声速解可由超声速解通过正激波扩压后得到。当|Z|≤2时，引射器出口壅塞。本文研究中，引射模态下二次燃料燃烧处于亚声速状态，因此仅取亚声速解。应用动量守恒方程可计算3处的总压为：

(11)

2.2.3 二次燃料喷注和壅塞特性

二次燃料与来流空气燃烧，放热产生的能量提高了燃气的总温。根据能量守恒，可以求得燃气总温：

(12)

其中：二次燃料与空气混合比f=mf/m3，mf为二次燃料流量，m3为3处空气总流量；hPR为反应热；ηb为燃烧效率。

1)亚声速燃烧。在引射模态、引射亚燃模态和双燃烧室亚燃模态，λ3<1，通过在3和4之间注入二次燃料，发动机在4处可形成壅塞，实现亚声速燃烧。因此，4处的速度系数λ4=1。忽略燃烧室阻力和燃料喷注的轴向速度，假定pt4=pt3，燃烧室出口面积A4也可通过连续性方程求得。

2)超声速燃烧。在双燃烧室超燃模态，λ3>1，燃烧室出口不壅塞。假定燃烧室压力恒定，燃料喷注方向垂直于流向。忽略燃烧室阻力和燃料喷注的轴向速度，动量守恒方程可以写为v4=v3/(1+f)，其中v3=λ3[2γ3R3Tt3/(γ3+1)]0.5，则λ4=v4/[2γ4R4Tt4/(γ4+1)]0.5，A4也可以通过连续性方程求得。

2.2.4 扩张段

假定扩张段是等熵膨胀，则pt10=ηept4，Tt10=Tt4，其中ηe为喷管效率。由此，速度系数λ10可由式(13)求得：

A4q(γ4,λ4)=A10q(γ4,λ10)

(13)

2.2.5 发动机推力

优化的目标函数是发动机比冲和推力。假定最优膨胀(p10-p∞)，则比冲和推力为：

(14)

(15)

2.3 基本的运动关系

图6 飞行器二维平面内受力示意Fig.6 Two-dimensional free-body force diagram

假定飞行器在二维平面内飞行，当机翼相对飞行轨迹倾斜时，会产生攻角α，从而产生相对于飞行轨迹垂直的升力。图6给出了二维平面内飞行器受力示意图。θ是飞行轨迹与水平面的夹角，ψ是推力方向与水平面的夹角，则飞行方向和法向的加速公式为：

(16)

其中，D和L分别是阻力和升力，

(17)

CD为阻力系数，CL为升力系数，v为速度，Aref为参考面积。

3 计算结果与分析

3.1 典型轨迹

采用火箭基组合循环发动机的临近空间飞行器，在低马赫数(0～2.0)段由于飞行速度较低，动压ρv2/2低，升力不足。如果要维持飞行轨迹向上，则需要足够大的推力分量平衡重力，但速度提升缓慢，推进剂消耗却非常可观。如果考虑初始就有一个倾斜向下的飞行轨迹，则重力分量mgsinθ可以为飞行器提供更大的加速度。虽然之后还需要转向，再次爬升，但考虑到较高飞行动压情况下比较可观的推力增强效果，这种初始倾斜向下投放的空中发射方式就非常值得尝试了。

(a) 参数随Ma的变化曲线(a) History of parameters versus Mach number

(b) 参数随飞行时间的变化曲线(b) History of parameters versus flight time图7 飞行器在11 km处以0.8马赫、θ=-30° 投放后的性能参数和轨迹参数Fig.7 Performance and trajectory parameters of a vehicle dropped at 0.8Ma and 11 km above sea level with an initial flight path angle of θ=-30°

3.2 轨迹优化

鉴于上述结果，要进一步研究飞行器轨迹参数对性能的影响，需要开展飞行轨迹优化。假设临近空间飞行器沿二维轨道平面飞行。在约10 km高度以0.8马赫的速度投放，发动机工作在引射模态；之后，加速到2.5马赫以上，转变工作模态，进入引射亚燃模态或双燃烧室亚燃模态；最终，在25～30 km高度达到6马赫，进入双燃烧室超燃模态，巡航至目的地。优化分析不考虑巡航与着陆。约束条件为最大动压不超过200 kPa、最大加速度为30 m/s2。

为了简化，采用飞行攻角α控制飞行器的飞行轨迹。攻角α变化范围为-5°～8°。为了开展采用数值方法求解优化问题，飞行攻角等优化设计参数需要离散化。基于这个方法，将攻角α和引射火箭总压ptp随马赫数变化的曲线分为9段。

优化计算考虑了如下设计参数：

1)飞行器进气道面积A0。

2) 2个引射火箭几何参数：φ*和φs。

3)初始轨道角度θ0和海拔高度y0。

4) 9段攻角α：α1，α2，…，α9。

5) 8段引射火箭总压ptp：p0R1，p0R2，…，p0R8；因为此时发动机进入双燃烧室超燃模态，故p0R9=0。

轨道设计的目的是找到一组设计参数使得飞行器达到巡航点设计参数(飞行马赫数Mac=6，飞行高度yc=26 km，轨道倾角为0)时，剩余质量最大。飞行速度达到巡航马赫数Mac时轨迹仿真结束，并计算误差，误差方程定义为:

δ=|y-yc|+|θ|

(18)

通过求解函数(18)的最小化问题，即可得到一条符合条件的轨迹(可行解)。采用MATLAB提供的遗传算法工具包求解轨迹可行解。

轨道优化的目的是找出剩余质量最大的一条轨迹及其对应的一组设计参数。采用Isight8.0进行了轨道优化计算。

3.2.1 空中发射与地面发射

当飞行器从地面发射时，由于飞行速度较低，飞行器的升力不足以克服重力，必须采用较大的初始飞行轨道倾角，利用发动机的推力来克服重力。这样就大大增加了推进剂的消耗速度。以初始飞行角θ0取值范围0°～90°、初始飞行高度y0=0 km、初始马赫数Ma0=0开展优化设计，并与空中发射方式(y0=11 km,Ma0=0.8)进行对比。优化计算结果表明空中发射和地面发射最优初始飞行角度θ0分别为-0.2°和86°，如图8所示。

(a) 参数随Ma的变化曲线(θ0=-0.2°)(a) History of parameters versus Mach number(θ0=-0.2°)

(b) 参数随Ma的变化曲线(θ0=86°)(b) History of parameters versus Mach number(θ0=86°)

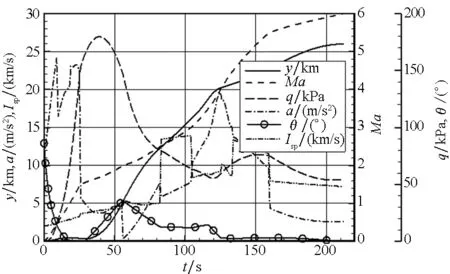
(d) 参数随飞行时间的变化曲线(θ0=86°)(d) History of parameters versus flight time (θ0=86°)图8 空中发射与地面发射的最优轨迹Fig.8 Optimal trajectories of the vehicle for air launch and surface launch

3.2.2 空中发射时初始轨道倾角θ0的影响

针对初始飞行轨道倾角θ0对飞行器轨迹参数和飞行器性能的影响开展了研究，图9给出了θ0为-29°、-12.5°和6.4°时的飞行器性能和轨迹参数。总的来说，初始飞行轨道倾角越小，动压越大，最低轨道高度越小。

优化计算获得的可行解如图10所示。当-20°≤θ0≤3°，m/m0变化范围为0.675～0.681，m/m0误差小于1%。这说明实际飞行时投放角度可以允许有一定的误差范围，具有较强鲁棒性。

(a) 参数随Ma的变化曲线(θ0=-29°)(a) History of parameters versus Mach number(θ0=-29°)

(b) 参数随飞行时间的变化曲线(θ0=-29°)(b) History of parameters versus flight time (θ0=-29°)

(d) 参数随飞行时间的变化曲线(θ0=-12.5°)(d) History of parameters versus flight time (θ0=-12.5°)

(e) 参数随Ma的变化曲线(θ0=6.4°)(e) History of parameters versus Mach number(θ0=6.4°)

(f) 参数随飞行时间的变化曲线(θ0= 6.4°)(f) History of parameters versus flight time (θ0= 6.4°)图 9 θ0对飞行器性能和轨道参数的影响Fig.9 Effect of initial angle θ0 on the vehicle performance and trajectory parameters