高超声速飞行器低可探测性滑翔弹道优化方法*
2019-10-14丰志伟葛建全许强强
黄 浩,丰志伟,葛建全,杨 涛,许强强
(国防科技大学 空天科学学院, 湖南 长沙 410073)
高超声速滑翔飞行器具有大射程、高速突防、再入段可机动等优点[1],是当前国内外研究的重点。与此同时,部分大国越来越重视对超声速进攻武器的防御,开展一系列有关拦截超声速飞行器的研究和试验。为了迎接这些潜在的挑战,使得高超声速武器具备更强的突防能力,必须着眼于现在和未来,研究如何有效克服这些威胁。隐身技术作为现如今提高武器突防性能最有效的技术之一,必将是首要选择[2]。
大多文献研究的是无人驾驶战斗机的低可探测飞行航迹规划问题[3-9],针对高超声速飞行器低可探测性弹道优化问题的研究很少,但文献中对无人机雷达散射截面(Radar Cross Section,RCS)数据处理的方法和如何在动力学模型中考虑隐身指标的方法都可以作为本次研究的参考。大部分文献仅考虑了平面内的低可探测航迹规划[3,5-8],郝震等[4]、陈璟等[9]综合考虑航迹规划和姿态控制,优化得到了具备隐身能力的飞行器三维航迹。
RCS数据随方位角变化十分剧烈,这使得RCS数据的处理是低可探测弹道设计中的一个难点。文献中对飞行器RCS的处理可大致分为两种:一是种采用简化的RCS分布模型[3-8],如圆模型[6]、椭圆模型[7]和蝴蝶模型[5]等;另一种是采用拟合函数拟合原始RCS数据[9-10]。第一种处理方法与实际的RCS数据分布差距很大;第二种相对贴切实际数据,但是拟合依然会对原始RCS数据特征造成较大的影响。
飞行器轨迹优化描述成数学问题,即在非线性条件下,含有状态、控制和终端约束的最优控制问题[11]。最优控制问题的解决方法通常分为直接法和间接法两种。伪谱法作为一种直接法,融合了两种方法的优点,获得数值解的同时能得到变量的精确信息,能以较好的效率计算最优控制问题[12],是求解最优控制问题普遍采用的一种方法。得益于其简单的结构,较高的精度和收敛速度,Radau伪谱法得到了快速发展[13]。hp自适应伪谱法将Radau伪谱法与hp型有限元法结合,在计算过程中自适应调整配点数和插值多项式的阶数,能够获得更高精度的解[12]。
针对文献中RCS处理方法导致RCS特征失真严重的问题,本文将基于180°×360°方向的RCS数据,采用三次样条插值来获取飞行器飞行过程中实时的RCS。原始RCS数据随方向变化十分剧烈,不利于收敛,故采用高斯滤波方法对其进行平滑处理,即光滑数据又保留其变化趋势,提高收敛性能。完成了面向低可探测性弹道优化问题的建模和仿真验证,通过坐标转换方法将雷达探测模型和飞行动力学模型耦合。以探测概率为目标函数,运用hp自适应Radau伪谱法优化求解,获得具备低可探测性能的滑翔弹道。
1 雷达散射截面仿真与处理
1.1 雷达散射截面仿真
CST(Computer Simulation Technology)微波工作室是一款功能强大的电磁仿真软件,其高频渐进求解器(Asymptotic Solver,简称A求解器)基于弹跳射线算法,考虑了目标边缘的衍射效应,对于电大目标RCS仿真具有较高的精度和效率。
运用A求解器对飞行器进行全方位角单站RCS仿真。计算状态:雷达波频率为8 GHz,单站水平极化,材料设置为理想电导体,计算方位角为θc∈[0°,180°]、φc∈[0°,360°],每一度取一个值。结果如图1所示。
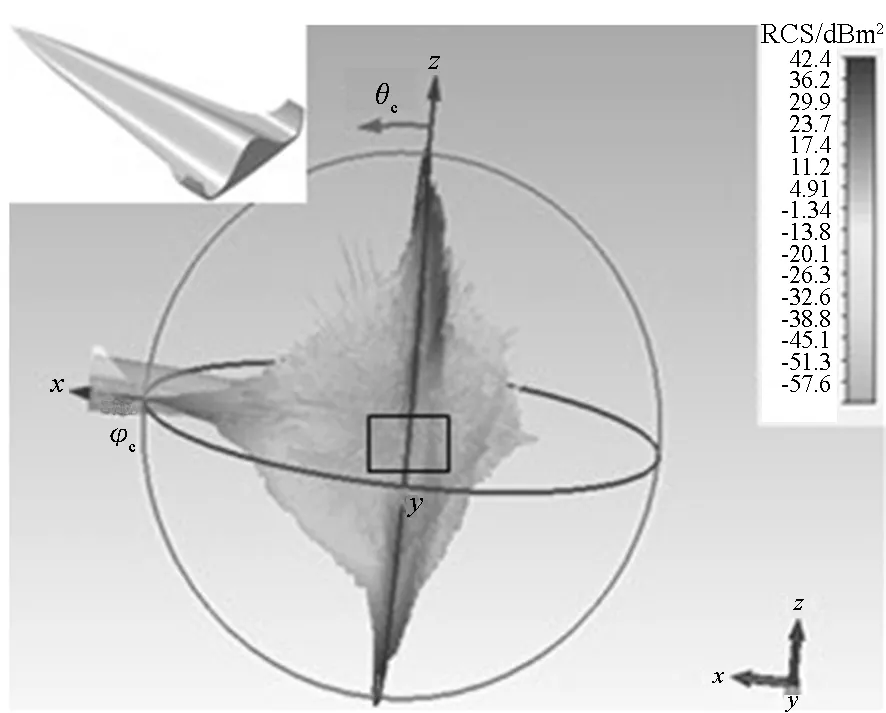
图1 高超声速飞行器及其RCS云图Fig.1 Hypersonic vehicle and its RCS distribution
可以看出,飞行器的整个RCS云图存在许多“毛刺”,不同方位的RCS值差距很大。在飞行器的尾部、腹部、左右两侧以及顶部区域, RCS值远高于其他区域。
飞行器飞越雷达时,它的侧面(φc=90°)必定要经过雷达。从RCS云图可以发现,飞行器侧面除了y轴附近的一小块区域RCS较低之外(图中黑色线框区域),其余部位的RCS很大(20~40 dBm2)。可以预测,飞行器以低可探测性轨迹飞越雷达时,应当调整姿态,使得侧面低RCS区域面向雷达。
1.2 RCS数据光滑处理
飞行器的RCS随方位角变化剧烈,优化过程中直接通过插值方法调用这样的数据将极大地影响收敛性能。从拦截目标的角度讲,雷达需要对目标进行一定时间步长的追踪方可锁定拦截,毛刺带来的短时间概率变化对雷达追踪效果影响较小,主要的影响因素为RCS的整体趋势。故在保证RCS变化趋势一致的情况下,考虑将原始数据进行光滑处理。RCS数据犹如存在噪音的信号,可利用高斯滤波对数据进行光滑处理。
高斯滤波是一种低通的加权滤波,对于数据光滑十分有效。高斯滤波原理认为,某一方位的RCS数值不仅与本身有关,还应当受到其相邻区域内RCS的影响,这种影响通过加权平均的方式来体现,权值由距该点的距离决定。高斯滤波函数为:
(1)
式中,σ为标准差,x与y的平方和表示影响域内其他点与中心点的距离。假设需要滤波的离散数据为N2维,影响域为n2,则离散高斯卷积核计算公式为:
(2)
由于权系数之和必须为1,对高斯卷积核进行归一化获得所需的权重系数为:
(3)
对应点的滤波值计算方法为:
(4)
考虑180×180个点的RCS数据(利用对称性),选择高斯核函数的影响域为180,方差为2,获得滤波结果如图 2所示。可以看出,采用高斯滤波法光滑效果十分明显,并且很好地保留了原RCS数据的变化趋势。
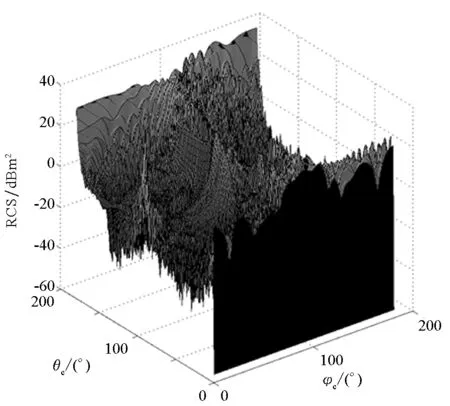
(a) 原始数据(a) Original data
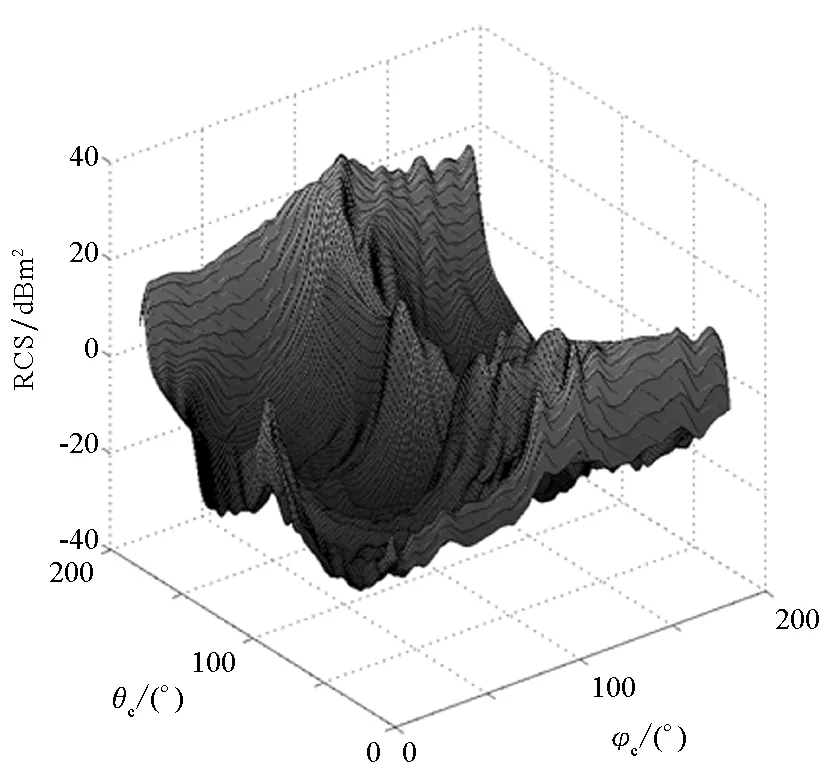
(b) 光滑数据(b) Smoothed data图2 高斯滤波法光滑数据Fig.2 Gaussian filtering method smoothing the RCS data
为评估滤波处理对结果的影响程度,以本文优化出的低可探测弹道为基准,对基于原始RCS数据所得概率曲线与滤波后所得的概率曲线进行对比分析,如图 3所示。
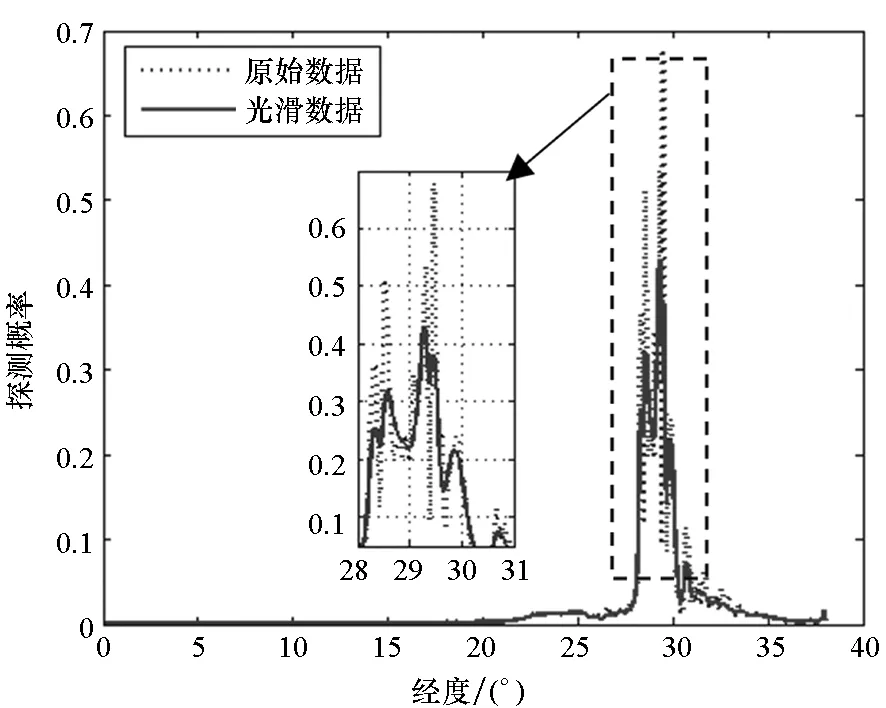
图3 滤波对概率的影响Fig.3 Influence of filtering on probability
从图3中可以看出,两条概率曲线基本吻合,不同的是基于原始数据的概率曲线在高概率区波动剧烈,峰值较基于光滑数据的概率曲线高出0.2左右,显然这是毛刺的影响所致。但高出的各个峰值的持续时间很短,在2~5 s之间,远低于防御系统雷达的反应时间(例如,俄罗斯的SA-6系统的反应时间为20~22 s[10])。所以,本文进行毛刺光滑处理对结果的低可探测性能影响不大。
2 飞行器动力学模型和雷达威胁模型
2.1 气动力模型
采用修正牛顿公式的面元方法,对模型的气动特性进行计算。计算攻角范围为-20°~20°(每一度计算一次)、马赫数范围为2~16(每间隔1计算一次)。计算出不同马赫数下升力系数随攻角变化曲线如图 4所示,图中曲线从上至下依次对应马赫数为2~16。
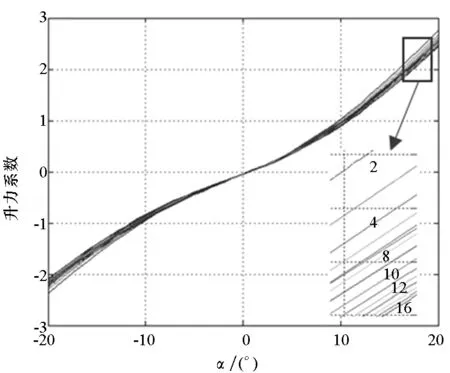
图4 不同马赫数下升力系数随攻角变化曲线Fig.4 Lift coefficient versus angles of attack at different Mach number
从图 4可以看出,在给定范围内,马赫数对气动力系数的影响远小于攻角的影响,故对于马赫数变化带来的影响不予考虑,认为气动力系数仅是攻角的函数。本次研究采用马赫数为10的气动数据,利用最小二乘法进行拟合,拟合函数为:
(5)
式中,CL为升力系数,CD为阻力系数,α为攻角,其余系数的值参见表 1。
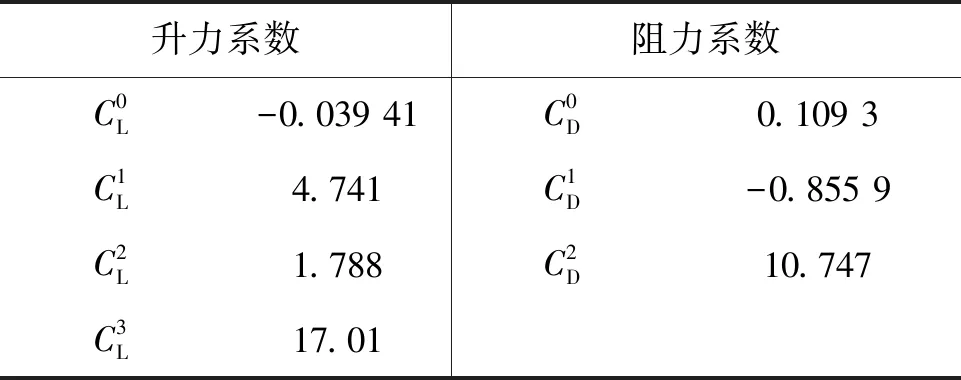
表1 拟合函数系数值
2.2 弹道模型
假设地球为均质圆球,不考虑地球自转和公转,滑翔飞行器的质点运动方程如下[14]:
(6)
式中,ν为倾侧角,m=1500 kg为飞行器质量,L和D分别为升力和阻力。状态变量见表 2,其中θ、σ和ν的定义如下。
θ:飞行器速度方向与当地水平面的夹角,速度方向指向水平面上方时为正。
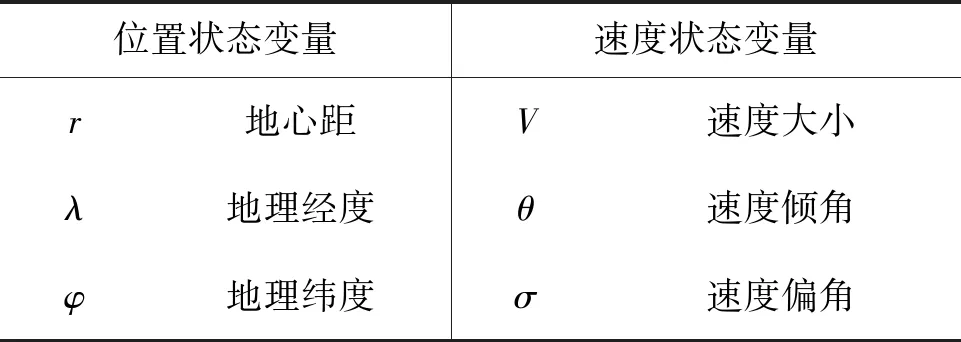
表2 运动方程状态变量
σ:当地正北方向与飞行器速度矢量在当地水平面投影的夹角,从正北方向顺时针转至速度投影位置为正。
ν:飞行器速度矢量所在铅垂面与升力方向的夹角,从飞行器的头部向后看时升力方向左倾为正。
2.3 雷达威胁模型
2.3.1 雷达散射截面计算模型
飞行的RCS特征和雷达与飞行器的相对位置有关,分别用φr和θr两个雷达方位角来描述雷达在飞行器体坐标系下的位置。两个方位角的符号定义为:从z轴正向看φr逆时针旋转为正,θr位于x1y1平面上方为正,如图 5所示。φr、θr和计算方位角φc、θc之间关系为:
(7)
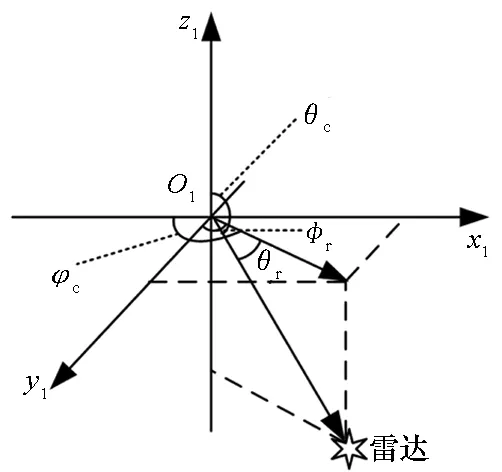
图5 体坐标系下的雷达姿态角Fig.5 Radar attitude angle in the body coordinate system
为了计算出φr和θr两个方位角,需要将飞行器的飞行状态和两个方位角进行耦合。采用坐标转换的方法,耦合思路为:选择一基准坐标系,计算出基准坐标系下雷达相对于飞行器的单位矢量x,通过坐标转换得到体坐标系下雷达相对于飞行器的单位矢量xb,最后利用三角函数关系求得φr和θr。具体如下:
1)选择基准坐标系。选择地心坐标系为基准坐标系。通过飞行器和雷达所在位置的经度、纬度和地心距计算它们在地心坐标系下的坐标(X,Y,Z)和(Xs,Ys,Zs)。则雷达相对于飞行器位置的单位向量为:
(8)
2)坐标转换。首先从地心坐标系转换至当地坐标系,再从当地坐标系转换至速度坐标系,最后由速度坐标系转换至体坐标系,对应的坐标转换矩阵分别为DE,VD,BV,得到体坐标系下雷达相对于飞行器位置的单位向量如下。
xb=BVVDDEx
(9)
3)计算φr和θr。令xb=(xb,yb,zb),利用数据的对称特性可计算出φr和θr:
(10)
得到φr和θr两个姿态角之后,利用式(7)计算出φc、θc,基于离散数据进行三次样条插值,计算出飞行器在当前位置下的RCS。
2.3.2 探测概率模型
只有当雷达探测到飞行器时,才会对飞行器构成威胁。一般将雷达威胁模型定义为探测概率,公式如下[8]:
(11)
式中,R为雷达和飞机之间的距离,单位为m。σ为飞行器RCS,单位为m2。c1,c2为与雷达有关的常数。
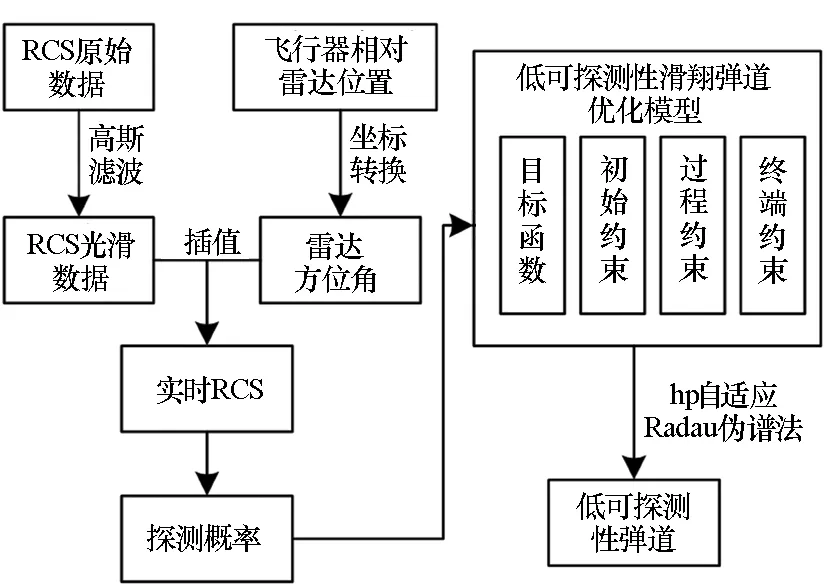
对于c1,c2两个常数的取值要能表征雷达探测的特点:当R大于雷达的最大探测距离Rmax时,P恒为零;当R小于最小探测距离Rmin时,飞行器无论以哪种姿态面向雷达,均会被雷达探测到,即P恒为1;当Rmin 图6 探测概率与R和σ的关系Fig.6 Detection probability versus σ and R 再入段飞行需满足作战任务要求,即使得飞行器在约束之内,到达指定作战空域,同时对飞行器末端攻击速度亦有限制。数学描述为对终端位置参数:地心距、地心经度、地心纬度和终端速度进行约束[15]: (12) 受到主动段关机点状态和攻击目标方位的影响,飞行器再入段的初始状态存在如下约束: Φ(t0)=Φ0 (13) 飞行器实际飞行过程中,攻角和倾侧角应当是连续变化的,同时受到过载和控制系统的限制,它们的变化率应当小于某一值,即 (14) 低可探测性轨迹优化的目的是找到一条从起始点到终点的飞行轨迹,飞行器在该轨迹上飞行,雷达探测到它的概率最小[9]。建立弹道优化的目标函数: (15) 高超声速低可探测性滑翔弹道优化问题的求解框架,如图7所示。 图7 低可探测滑翔弹道优化问题求解框架Fig.7 Solving framework for low detectable glide trajectory optimization problem 分别以飞行时间最短和探测概率对路径的积分最小为性能指标,优化得到最短飞行时间弹道(Minimum Time Trajectory, MTT)和低可探测性弹道(Low Observable Trajectory, LOT)。对比两种弹道,验证低可探测性滑翔弹道优化方法的有效性。 3.2.1 最短飞行时间弹道 1)问题分析。对于最短飞行时间弹道,飞行器为实现飞行时间最短的目的,飞行轨迹应该位于始端和终端连线的纵平面内。 2)参数设置。仿真相关参数设置如表3所示。 表3 相关参数设置 性能指标为飞行时间最短,即到达终端的时间最小,目标函数为: J=tf (16) 3.2.2 低可探测性弹道 在最短飞行时间弹道的基础上,以最小探测概率为优化目标函数。为了提高优化的效率和收敛性,采用以下逐步计算的方法:首先对光滑后的RCS数据进行多项式拟合,利用拟合函数进行低可探测弹道优化,得到一组解;然后基于离散的光滑数据,采用三次样条插值函数计算RCS,将上一步所得解作为初始猜测,仿真得到低可探测性优化弹道。 1)问题分析。为达到低可探测目的,飞行器应当尽可能远地绕飞雷达,但受到飞行能量的限制,它不得不经过雷达威胁区域。在雷达威胁区域,飞行器应当通过姿态调整将低RCS方向面对雷达。 2)参数设置。在最短飞行时间优化问题的基础上,目标函数修改为: (17) 3.2.3 优化结果 结果如图8所示,图8(b)中六角星为雷达,黑色虚线圆为雷达的探测范围。从图8(a)中可以看出,飞行轨迹为典型的滑翔跳跃弹道。 两种弹道均满足了给定的约束条件,不同的是飞行轨迹、终端速度、飞行时间、雷达方位角轨迹(雷达方位角在RCS云图上的轨迹)和探测概率等,下面对这几个方面进行对比分析。 飞行轨迹:如图 8(b)所示,MTT位于纵平面内以减少飞行时间;LOT对雷达进行了绕飞,绕飞既可以增加飞行器与雷达之间的距离,同时又方便飞行器在飞越雷达时调整姿态将低RCS方位面向雷达。结果与之前的分析相一致,从而证明了结果的可靠性。绕飞带来了一定的航程损失,约为66.9 km,相比于4225 km的射程,损失并不算大。 终端速度:如图 8(c)所示,MTT的终端速度为1242 m/s,LOT的则为1000 m/s,可见LOT在满足终端约束的前提下尽可能远距离绕飞雷达,证明了本文提出方法的合理性。绕飞带来的速度损失为242 m/s,约为终端速度的1/5。 雷达方位角轨迹:如图 8(d)所示,MTT的雷达方位角轨迹经过了飞行器侧面的高RCS区域,而LOT的则避过了高RCS区域,从RCS较小的区域经过,这与之前的预测(1.2节)是一致的。从图 8(f)中可以看出,在经度为30°左右的时候,飞行器侧面刚好面向雷达,飞行器倾侧角从-13°左右增至-5°左右,即飞行器通过调整姿态角使得侧面低RCS区域面向雷达。 探测概率:如图 8(e)所示,MTT的探测概率峰值已经接近1,而LOT的仅有0.4左右。在雷达威胁区域,MTT的概率曲线基本一直位于LOT的上方,探测概率是LOT的2~5倍。 时间对比:假设P≥0.1时认为飞行器处于暴露状态。表4给出了MTT和LOT的暴露时间和飞行时间对比结果。相比于MTT,LOT多耗时101 s,但是暴露时间却少了238 s,暴露时间比例约是MTT的1/4。 上述对比说明,通过低可探测性弹道优化,虽带来一定的航程损失和速度损失,但是能够有效减小高超声速滑翔飞行器被发现的概率,提高其突防性能。 (a) 高度随经度变化曲线(a) Height versus longitude (b) 轨迹地面投影(b) Ground track (c) 速度随经度变化曲线(c) Velocity versus longitude (d) 雷达方位角轨迹(d) Radar azimuth track on the RCS contour map (e) 探测概率随经度变化曲线(e) Detection probability versus longitude (f) LOT 飞行轨迹控制量(f) Control quantity of LOT versus longitude 图8 优化结果 表4 暴露时间和飞行时间对比 本文提出了一种高超声速飞行器低可探测性滑翔弹道优化方法。基于飞行器180°×360°方向的RCS,采用插值方法计算飞行器在飞行过程中的实时RCS,最大限度地保留原始RCS数据的特征。运用高斯滤波法对RCS进行光滑处理,既不改变原数据趋势又加以平滑,提高优化问题收敛性能。完成了高超声速飞行器低可探测性滑翔弹道优化问题的建模,以探测概率为目标函数,运用hp自适应Radau伪谱法优化求解,采用逐步计算策略进一步提高优化效率和收敛性能。与传统最短飞行时间弹道对比表明,该方法能够有效降低雷达对飞行器的威胁。研究的成果在一定程度上为未来高超声速飞行器弹道方案设计提供理论和技术上的支持。 同时研究依然存在不足,比如仅考虑了单个雷达的情况、弹道的过程约束也过于简单等,下一步的工作将要考虑雷达组网下的低可探测性轨迹优化,并加入过载、气动热和动压等过程约束,同时可以进一步考虑激波和电离效应对RCS的影响。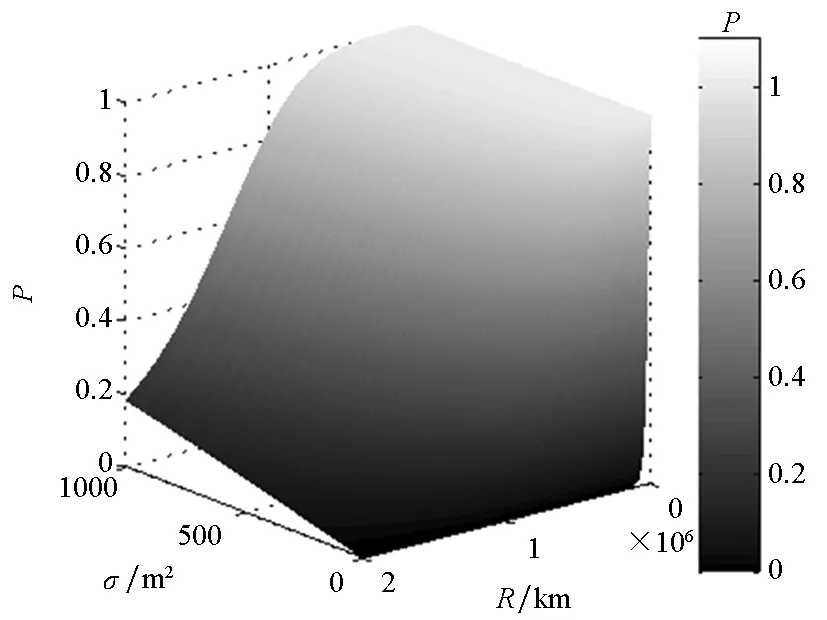
3 低可探测弹道优化设计
3.1 低可探测弹道优化模型
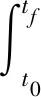
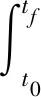
3.2 弹道优化仿真

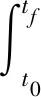
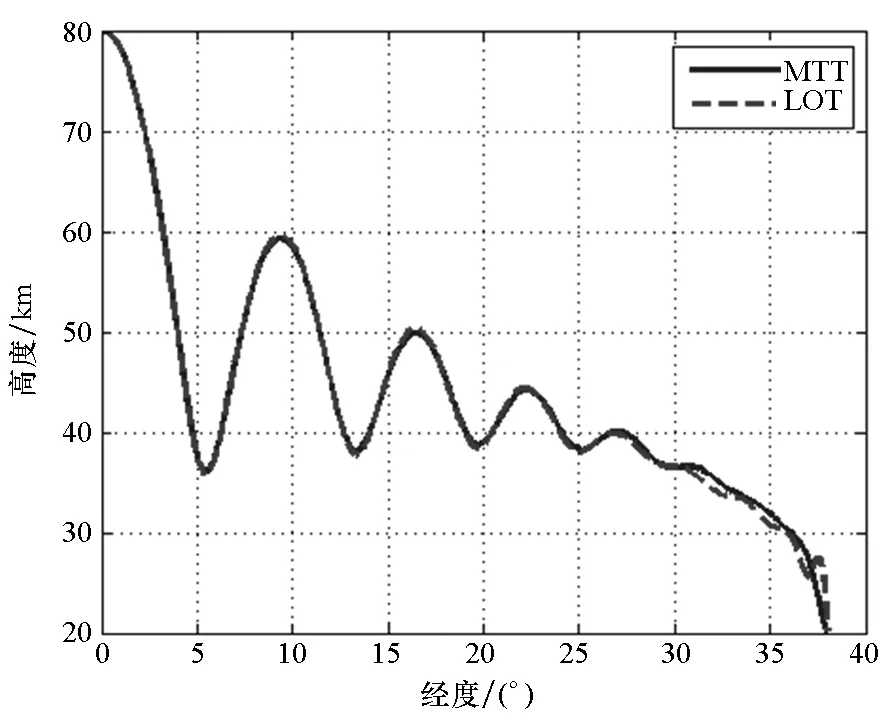
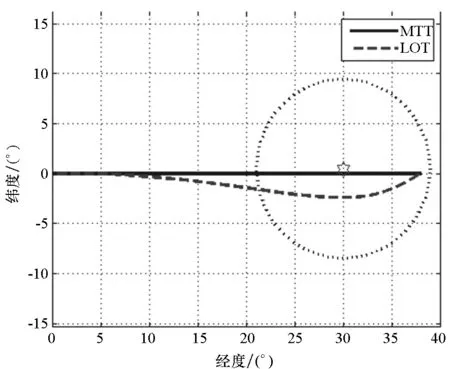
Fig.8 Optimization results
4 结论
