储能用蓄电池模型参数的动态辨识*

柳应全，鲁军勇，龙鑫林，魏静波，周 仁，吴羿廷

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

当前锂离子电池作为一种高效安全的二次能源越来越广泛地应用于新能源汽车、风力发电、独立光伏系统和大规模储能系统等领域。在舰载电磁发射武器中，锂离子电池组作为系统的初级储能环节，在舰船电网和脉冲电容器之间起着能量缓冲和功率放大的作用。

为了实现高功率输出，蓄电池储能系统经常涉及数千节单体电池串并联应用，需要管理的电池数量巨大且储能电压高达近万伏。若不能实施实时的监控和管理，将会出现放电的木桶效应和过充过放现象，极大地缩短单体电池的有效寿命，造成能源资源的浪费，情况恶劣时甚至会出现漏液、爆炸等危险事故。因此，锂离子电池模型未知参数的辨识，在电磁发射领域有着十分重要的作用。

锂离子电池的模型参数分为两种：一种是内电路参数，如平衡电动势、内阻和极化参数等，是等效电路中实际存在的用以表征电池充放电特性的量；另一种是状态参数，如SOC和SOH，是人为设计用于描述电池剩余电量和老化程度等状态的指标。这些参数的一个重要特点是无法进行直接观测，因此，针对锂离子电池的建模和参数的辨识一直是研究的热点和难点。

一直以来，SOC被认为是评价锂离子电池剩余电量的一个重要指标。估算SOC的方法可分为四种[1]：安时积分法、开路电压法、智能算法和组合算法。其中，安时积分法[2]被认为是最有效的方法，但该方法的缺陷是存在累积误差，尤其是在强电磁噪声、强电流脉冲的电磁发射环境下，对测量设备和信号处理单元都提出了较高的要求。另外，采用安时积分法往往很难确定初始的SOC，针对该方法的改进一般是在静态时先通过开路电压法进行SOC校准，而处于放电平台期的SOC状态很难通过开路电压进行估算。针对内电路参数估算的一个较为可行的办法是通过采集关键信息来进行。比如，采集放电初始阶段的电压跌落作为估算电池内阻的依据[3]，采集恢复过程用以评估模型中阻容网络的极化参数[4]。这种方法在实验室工况下效果较好，但在多物理场耦合、连续快速短脉冲放电的电磁发射工况下很难奏效。

本文在改进的Thevenin模型基础上，采用多元线性回归模型[5]对蓄电池内电路参数(内阻RS、极化电阻RD和极化电容CD)进行辨识，提出等效电容量Ce的概念用以表征蓄电池组的容量特性。

1 锂离子电池模型

1.1 改进的Thevenin模型

关于电池模型的研究论文有很多[6-8]，根据建模机理可以归纳为电化学模型[6-7]和等效电路模型[9]。由于在电磁发射应用中多采用多个锂电池串并联结构以实现更高的功率输出，因此，研究仅针对蓄电池组等效模型。目前应用较为广泛的是Thevenin模型[9-10]，如图1所示。其中，Eo表示蓄电池平衡电势，RS表示电池内阻，RD和CD用于表征电池的极化特性。

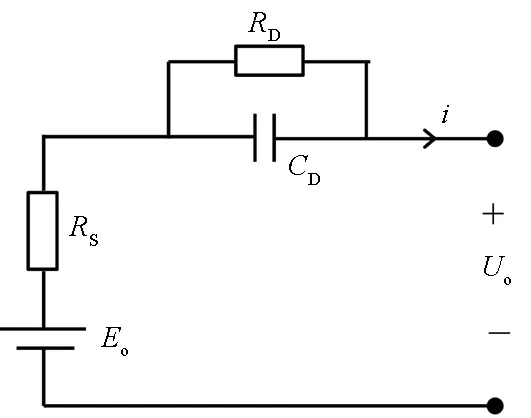
图1 Thevenin模型Fig.1 Thevenin battery model

Thevenin模型由于未考虑电池的容量范围、充放电截止电压和老化效应，在实际使用中存在一定的局限性。分析研究是建立在改进的Thevenin模型基础上的，如图2所示。Vccv和Vdcv分别表示蓄电池的充电和放电截止电压，Ce表示等效电容量(单位为F)，随着电池的老化和SOC区间而变化，可从电池出厂测试的OCV-SOC变化曲线提取。

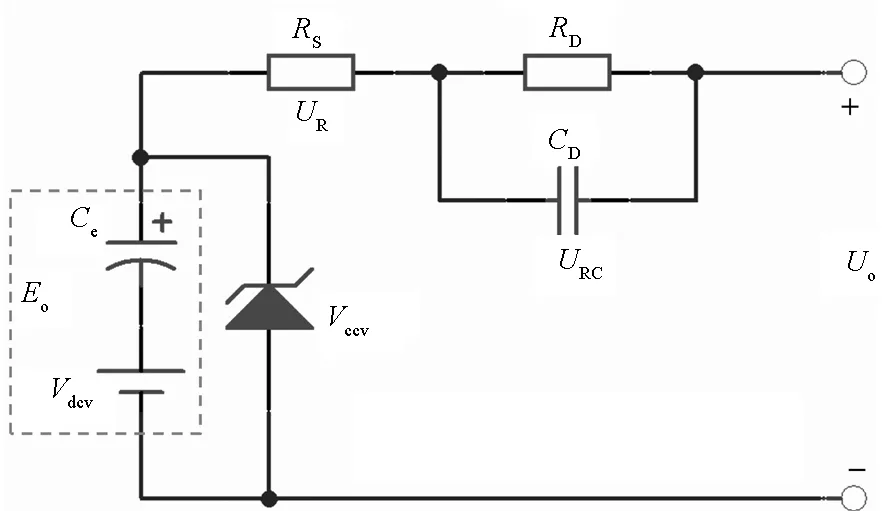
图2 改进的Thevenin模型Fig.2 Improved Thevenin model

1.2 等效电容Ce的提取

某型磷酸铁锂电池的Eo-SOC曲线如图3所示，呈马尾状分布。由于曲线在平台期(AB段)和BC段可近似为直线，且电池很少位于OA段工作，因此，可以作线性化处理得到平衡电势Eo和SOC之间的线性表达式。

(1)

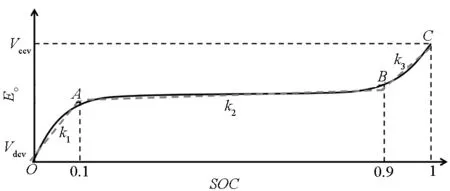
图3 某型磷酸铁锂电池的Eo-SOC曲线Fig.3 Eo-SOC curve of a LiFePO4 battery

等效电容量Ce定义为电池平衡电动势变化1 V所对应的双层电极板上电荷变化量：Ce=Δq/ΔEo=QN·ΔSOC/ΔEo。其中，Δq为双层电极板上电荷变化量，ΔEo为电动势变化量，QN为电池额定容量，ΔSOC为SOC变化量。由式(1)可得：

此处等效电容量Ce的提取方法仅用于获取初始值，由于该量在循环周期和寿命周期内不断波动，且随电流倍率的变化也有差异，因此，应在循环周期内对其进行动态辨识。

2 改进的模型参数辨识方法

2.1 线性回归模型

锂离子电池模型参数辨识的方法有最小二乘法[11]、卡尔曼滤波法[12]、神经网络法[4, 13]、遗传算法[14]和粒子滤波法[15]。线性回归方法是最小二乘法在一元及多元线性估计方面最广泛的应用。此处参照文献[11-12, 14]中的推导结论直接给出离散域的差分方程：

V(k)+a1V(k-1)=b0I(k)+b1I(k-1)

(2)

式中：V(t)=Eo(t)-Uo(t)，Eo(t)和Uo(t)分别表示蓄电池组平衡电势和输出端电压；a1，b0，b1是待估计参数，且满足

其中，T表示采样周期。

锂离子电池的模型参数为：

2.2 考虑初始条件的线性回归模型

文献[11-12, 14]中的推导在对时域表达式进行Laplace变换时未考虑变量的初始条件，因此，当初值条件不为零时，式(2)不再成立。连续时域表达式为：

V(t)=RSi(t)+URC(t)

取采样周期为T，对上式进行离散化得到差分方程：

V(k)=RSi(k)+URC(k)

(3)

(4)

将式(4)代入式(3)，得：

(5)

由式(3)，得：

URC(k-1)=V(k-1)-RSi(k-1)

(6)

再将式(6)代入式(5)，可得：

(7)

式(7)也可改写成形如式(2)的差分方程形式，只不过待估计参数a1、b0和b1分别满足：

其中，τ=RDCD表示一阶RC网络的时间常数。

3 SOC的动态辨识

单体锂离子电池的单脉冲放电试验曲线如图4所示。可以看出，由于松弛效应[16-17]，放电结束后，电池端电压需要几个周期才能恢复到稳定值，此时电池的开路电压一般等于平衡电动势Eo。这一特性可用于在长时间尺度下辨识等效电容Ce。

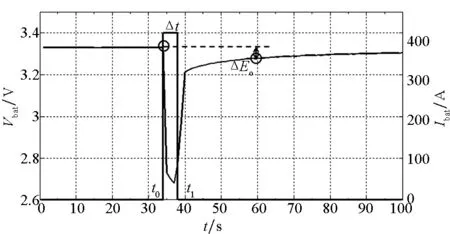
图4 单体电池单脉冲放电曲线Fig.4 Single pulse discharging curve of a battery cell

由于电荷守恒，等效电容Ce上的电荷损失应与锂离子电池的放电深度相对应，即：

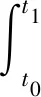
(8)

因此，等效电容Ce为：

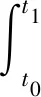
式(8)可以改写成差分形式：

(9)

将式(9)代入式(7)，并化简得：

(10)

考虑测量噪声εk，式(10)可以写成以下离散形式：

Uo(k)-Uo(k-1)

(11)

令：H(k)=[(Eo-Uo)(k-1)i(k)i(k-1)]，Θ(k)=[a1(k)b0(k)b1(k)]T，Ym(k)=Uo(k)-Uo(k-1)。

当数据长度为m时，有：

蓄电池的平衡电动势Eo在放电的过程中可以被间接观测。由图3可知，Eo和SOC之间存在一一对应关系。由于普遍认为电池SOC位于小于0.1和大于0.9区间时可以较准确地采用开路电压法进行SOC估算[18]，本文的SOC动态辨识仅针对SOC位于0.1～0.9区间进行。

(12)

式中：Ce1和Ce0分别是SOC处于高区间和低区间的等效电容量；Ce是当前辨识的等效电容量；Vccv和Vdcv是单体电池安全工作的一个重要属性，在其生命周期内一般保持不变。因此，间接观测Eo即可实现SOC的动态辨识。采用式(12)计算SOC的优势是不需要知道初始SOC是多少，由于Eo可通过静态时直接测量开路电压得到，因此该方法较适用于平台期的SOC辨识。由于电池SOC和Eo属于快速变化的特征量，需要在短时间尺度下进行观测和辨识；而Ce属于缓慢变化的物理量，可以在长时间尺度下进行观测。

4 仿真实验分析

所采用的实验工况为蓄电池组在一个循环周期内对纯电阻负载连续脉冲放电，脉冲周期为4 s，间隔4 s。蓄电池组端电压曲线和放电电流曲线分别如图5(a)和图5(b)所示。

(a) 蓄电池组端电压曲线(a) Terminal voltage curve of the batteries

(b) 放电电流曲线(b) Discharging current curve图5 试验采集曲线Fig.5 Test measured curves

分别采用差分方程(2)和差分方程(11)对试验采集数据进行辨识，在脉冲放电阶段，分别以H(k)向量作为特征量，以Y(k)向量作为输出量，对系数向量Θ(k)进行递推辨识。辨识结果如图6～8所示。

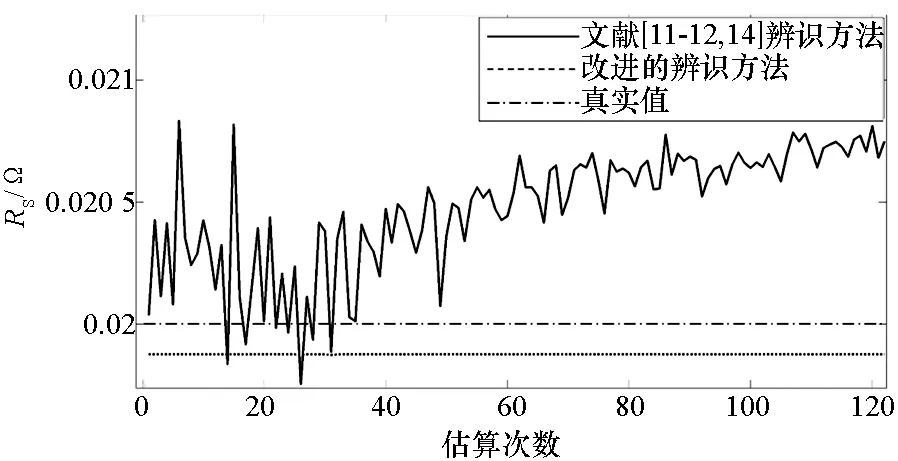
图6 内阻RS的辨识结果Fig.6 Identified internal resistance RS results

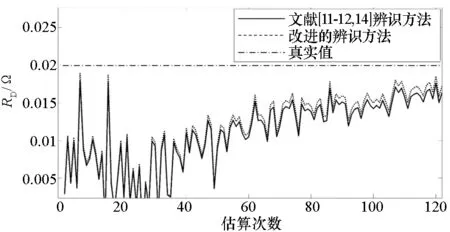
图7 电阻RD的辨识结果Fig.7 Identified resistance RD results

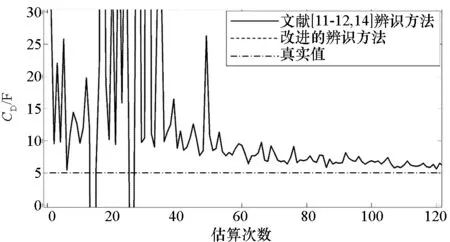
图8 电容CD的辨识结果Fig.8 Identified capacitance CD results

可以看出，改进后的辨识方法在内阻RS辨识上有极大的优势，收敛快，鲁棒性好，估算误差只有0.5%。电阻RD和电容CD的辨识结果比较接近，由于测量噪声的影响，初始阶段辨识结果波动较大，图8中改进的辨识方法与文献[11-12，14]辨识方法的误差几乎一致，但整体上看，改进的辨识方法由于考虑了初始条件，比文献[11-12, 14]中采用的方法误差小一些。

筛选静置5τ～10τ(τ=RDCD为阻容网络的时间常数)时间的开路电压Uo的差值，并累计放电期间的总电荷变化量Δq。采用式(8)提到的等效电容辨识方法，可得一个循环周期内等效电容量Ce的辨识结果，如图9所示。

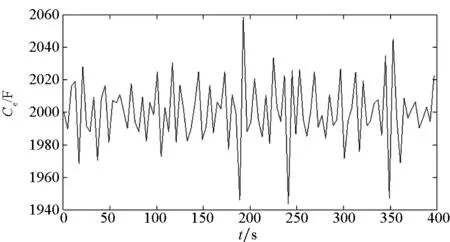
图9 等效电容量Ce的辨识结果Fig.9 Identified equivalent capacitance Ce results

从图9可以看出，相对于采集周期T而言，Ce在较长的时间尺度内波动，将辨识得到的Ce代入式(9)，即可得到短时间尺度内Eo的变化曲线，如图10所示。

再在短时间尺度内将辨识得到的Eo实时代入式(12)即可得到一个循环周期内锂电池SOC的变化曲线，如图11所示。

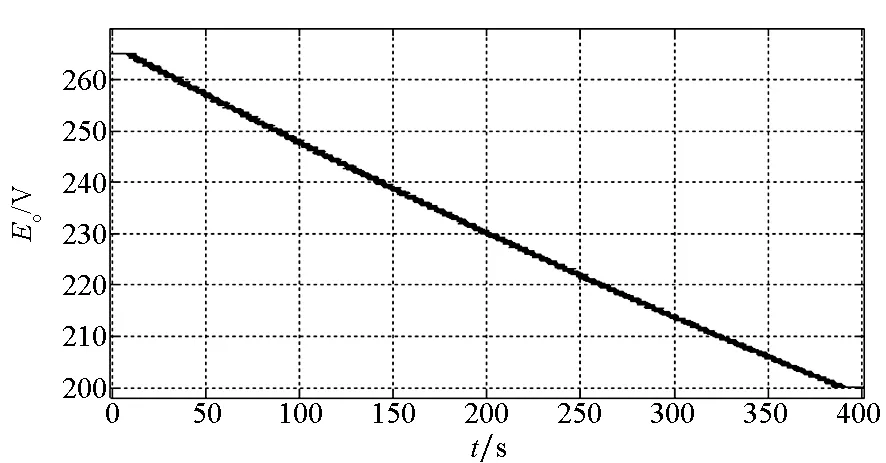
图10 蓄电池平衡电动势Eo的辨识结果Fig.10 Identified batteries balance electromotive force Eo results

(a) 动态辨识结果(a) Dynamic identified results

(b) 辨识误差(b) Identified error图11 SOC的动态辨识结果和辨识误差Fig.11 Identified SOC results and identified error

可以看出，SOC动态辨识结果与理想SOC值较为一致，在SOC区间的中段误差最小。因此，所提SOC动态辨识方法是有效而且准确的。

5 结论

本文改进了传统的线性回归模型，推导出一种更加精简可行的内电路参数辨识方法，并提出通过间接观测蓄电池平衡电动势来动态辨识SOC的方法。以改进的Thevenin电池模型为基础，等效电容量被用来作为评估锂电池组容量特性的物理量，可以通过在长时间尺度上观测静态开路电压的变化量和电荷变化量来获取。仿真实验和分析验证了以下结论：

1)考虑初始条件的线性回归算法相比于传统的线性回归算法能得到更好的辨识结果；

2)所提SOC动态辨识算法能够准确地辨识电池的SOC参数。