卫星遥测数据相关性知识发现方法*
2019-10-14杨甲森王春梅
杨甲森,孟 新,王春梅
(1. 中国科学院 国家空间科学中心 复杂航天系统电子信息技术重点实验室, 北京 100190; 2. 中国科学院大学, 北京 100049)
航天器遥测数据是地面运管系统判断其在轨运行状态的唯一依据[1]。作为典型复杂系统,航天器所包含的供配电、姿控、轨控、热控、有效载荷等分系统[2]之间、分系统内部各模块之间,均存在着大量电气、数据、热控接口以及复杂的系统交互,这就决定了反映星载设备状态的遥测数据之间普遍存在着相关关系。掌握这些相关关系对于实现多元遥测数据的关联检测、航天器异常事件原因的深层次挖掘以及特征选择和数据降维等都具有十分重要的意义。
围绕变量相关性,国内外学者提出了多种有效的相关性度量方法。其中Pearson相关系数[3]、最大信息压缩指数[4]、最小平方回归误差等被广泛用于度量变量间的线性相关,但难以刻画遥测变量间普遍存在的非线性相关;互信息[5]、信息增益比等测度虽然能够同时对线性相关和非线性相关进行度量,但这些测度依赖的概率密度函数的估计较为困难[5-6],且不具有普适性和等价性[7]。2011年,Reshef等[7]通过基于网格划分的互信息估计思想提出的最大信息系数(Maximal Information Coefficient, MIC),不但能够同时刻画变量间线性相关和非线性相关,而且对函数、超函数以及分段函数关系的度量都十分有效,具有较好的普适性和等价性,被广泛应用于复杂装备监测数据[8]、航天器遥测数据[9]的相关性分析。然而,在将MIC方法应用于高维度、大规模卫星遥测数据的相关性分析时,存在以下问题:①算法时间复杂度高,即使基于动态规划的近似算法,时间复杂度也达到O(n2.4)[10];②MIC测度偏向于多值变量,取值较少变量的得分往往偏小。提高MIC算法的精度和性能历来是相关性研究的两大热点。文献[11]基于二次优化过程提高了MIC精度但却再度提高了复杂度;文献[12]采用图形处理单元和现场可编程门阵列组成的异构加速器提高了MIC计算的性能;文献[13]提供了一种基于并行处理的MIC快速计算跨平台工具;文献[14]基于MapReduce模型对MIC算法进行了并行化设计;文献[15]采用C语言重新实现了MINE套件。上述文献针对MIC算法性能提升的研究,多是围绕硬件环境、并行运算等算法实现的方式展开,并未改变其等深划分后基于动态规划算法寻优的本质。此外,已有文献尚无关于MIC测度偏向多值变量问题的讨论。
1 最大信息系数
1.1 MIC算法原理
MIC是以互信息为基础的,其主要思想是基于一种认识:如果两个变量存在相关关系,那么可以在两个变量构成的散点图上绘制网格,数据在网格中的分布情况可以反映二者之间的相关关系。网格绘制中,MIC方法考虑两个因素:①网格划分的数量;②网格划分的方法。其原理可通过以下定义[7]来说明。
定义1(特定划分下最大信息系数I(D,s,t))对二维有序对数据集D(X,Y),分别在X、Y方向上进行s、t段划分。定义该划分对应的网格为G,G划分下D的概率分布为D|G、互信息为I(D|G),那么此划分下的最大信息系数为:
I(D,s,t)=maxI(D|G)
(1)
式中max的含义是指:将二维变量划分为s、t段的方法有多种,如等宽、等深划分[16],每一种方法对应不同的互信息值,I(D,s,t)为其中的最大值。I(D|G)计算方法如下:
(2)
式中,p(s,t)为联合概率密度,p(s)、p(t)为边缘概率密度。根据大数定理,当观测数据量足够大时,p(s,t)的计算可用落入网格中的样本数量占比来近似,p(s)、p(t)分别用落入(k,k+1)和(l,l+1)网格的样本数量占比来近似,其中k∈[0,s-1],l∈[0,t-1]。
定义2(特征矩阵M(D))特征矩阵M(D)第s行、t列元素的定义为:在s,t段网格划分下的最大信息系数(定义1)的归一化矫正,如式(3)。s,t为任意正整数,即M(D)是无限维矩阵。
(3)
定义3(最大信息系数MIC(D))设D的样本容量为n,那么:
MIC(D)=maxst≤B(n){M(D)s,t}
(4)
式中,B(n)为网格划分数量的上限,它将特征矩阵M(D)限定为有限维,文献[7]给出了B(n)的推荐值为n0.6。
1.2 基于动态规划的MIC近似算法
在计算I(D,s,t)时,为了避免网格穷举切割,进行遍历寻优,降低MIC方法计算的复杂度,文献[7]提出了一种基于动态规划算法来近似求解MIC的方法。详细步骤如下:
步骤1:在X方向,以等值样本落入同一网格为原则,确定X方向s=2段的等深划分Q,如图1所示。等深的含义是指,划分后每一个分段的样本点数相差不多。

图1 X方向等深划分Fig.1 X direction equal partition
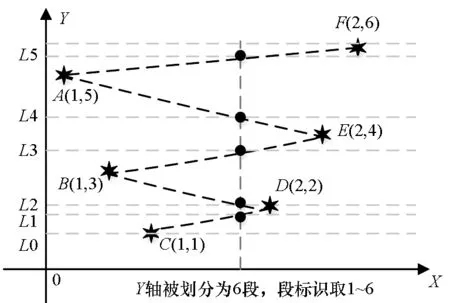
图2 Y方向候选划分Fig.2 Y direction candidate partition
步骤2:在Y方向,以等值样本落入同一网格为原则,确定Y方向候选划分P,如图2所示。其方法是以X方向分割线与数据曲线(按Y值升序顺序,逐点连接而成的线)的交点作Y轴的垂线,Y方向等值样本若不在同一X划分Q中,则需增加一个Y方向的候选划分。
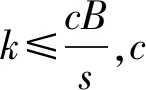
F(cr,2)
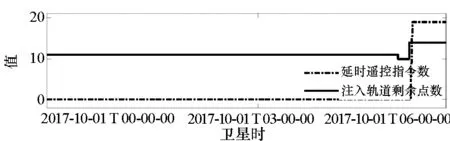
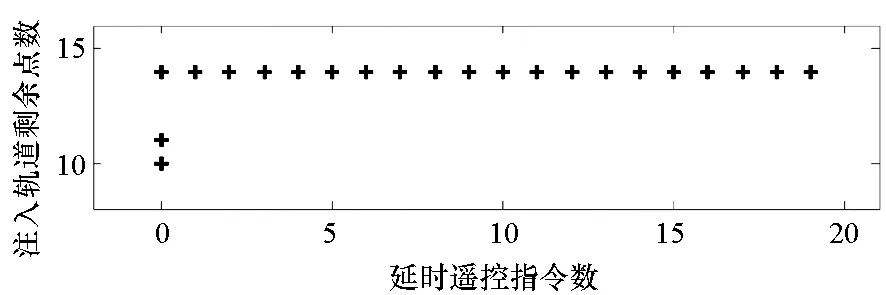
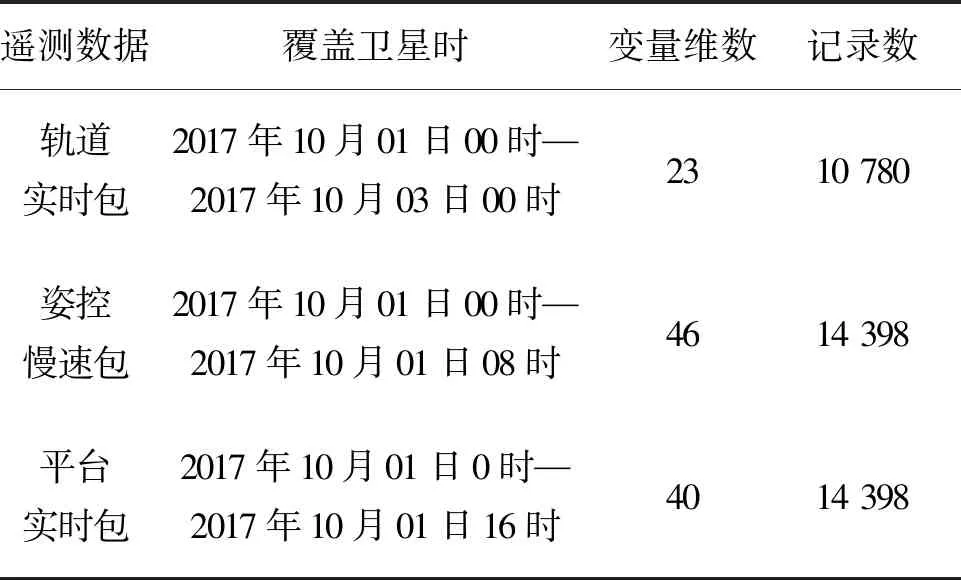
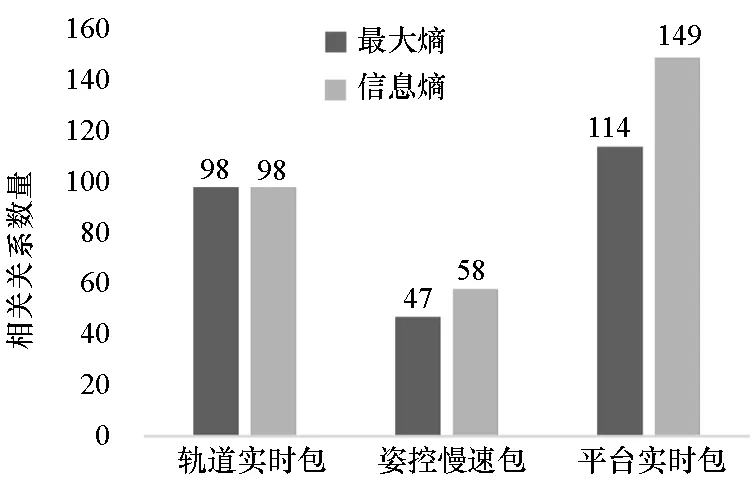
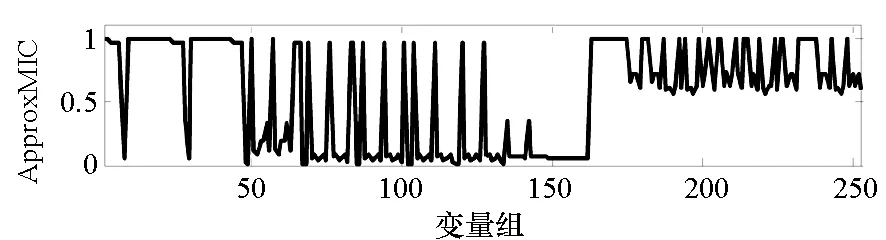
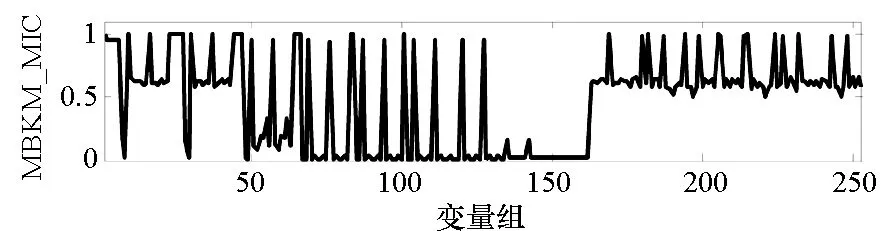
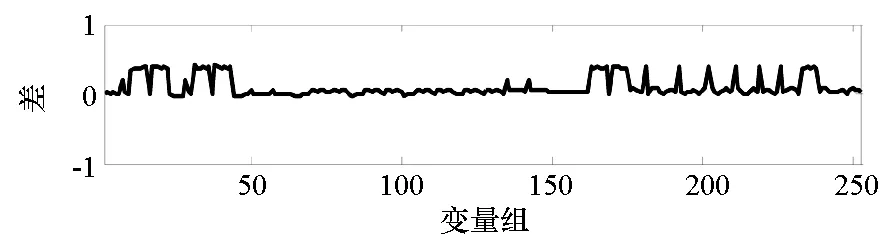
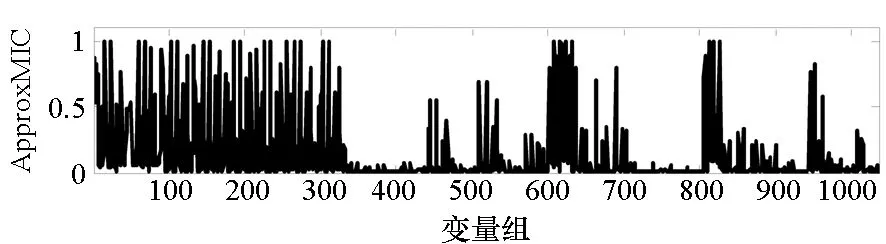
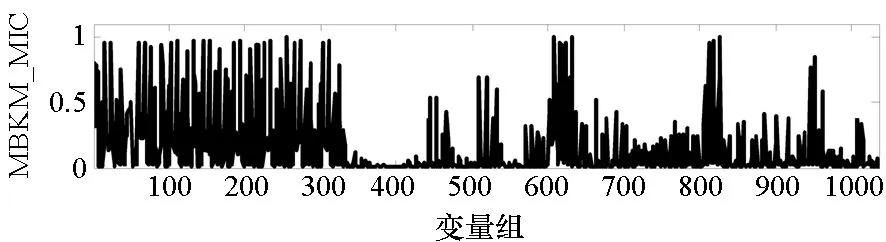
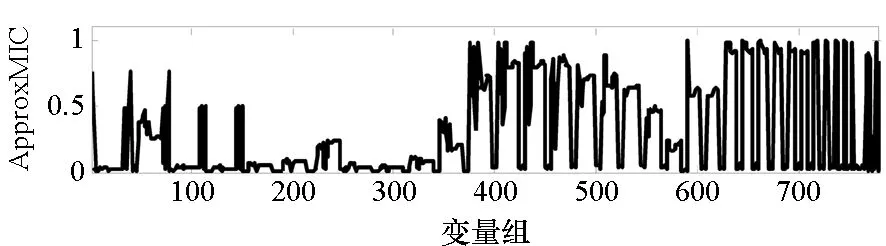
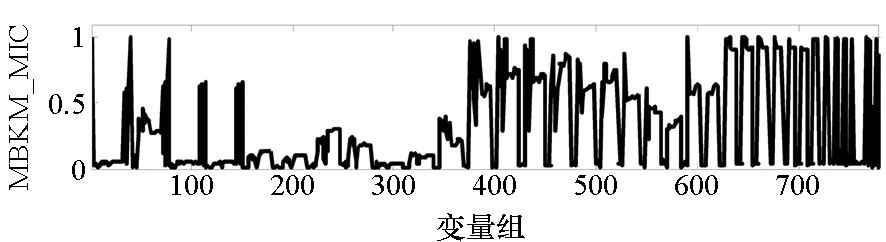
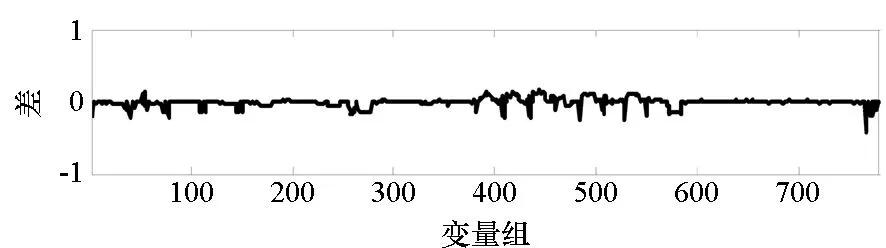
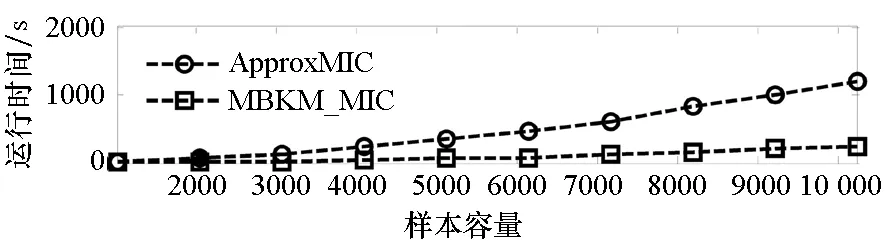
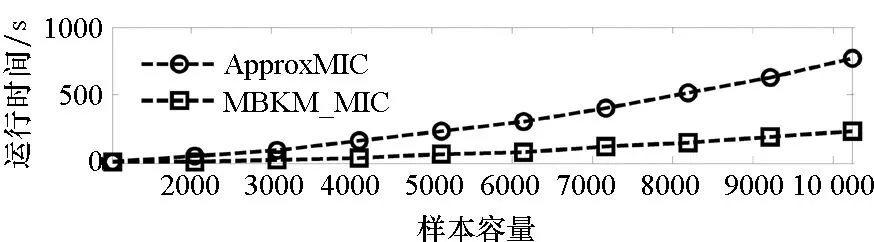
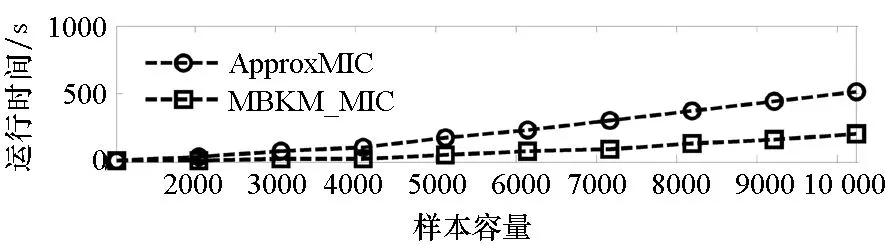
=max1≤i (5) F(cr,l) (6) F(ck,l)是所有样本l分段下,H(P)-H(Q,P)的最大值。由于互信息I(Q;P)=H(Q)+H(P)-H(Q,P),在X方向Q划分不变的情况下,H(Q)为定值,因此F(ck,l)+H(Q)即为所有样本l分段下的最大互信息值。 步骤7:将纵坐标与横坐标交换,重复步骤1~6,求得Y方向等深划分下的特征矩阵MY(D)。 步骤8:以两个特征矩阵MX(D)、MY(D)中的最大元素作为两个变量的MIC值。 近似算法计算量主要集中在步骤4,即动态规划算法求F值部分,该部分时间复杂度为O(k2st)[7],等深划分循环次数为B/2,因此其整体复杂度为O(k2stB)=O(k2B2)=O(n2.4)。 Mini BatchK-Means算法是K-Means算法的变种。与传统K-Means方法相比,Mini BatchK-Means在每次迭代更新质心的过程中,采用随机抽样获得的数据子集进行更新。实践证明Mini BatchK-Means在数据量较大时,可以有效地减少算法收敛时间,但其准确度稍有下降[17]。 给定样本集Z={z1,…,zn},n为样本容量。Z将被划分为k个簇,簇的中心为C={c1,…,ck}。Mini BatchK-Means聚类的迭代步骤如下。 步骤1:从Z中随机选择k个样本作为初始中心C。 步骤2:从Z中随机抽取容量为b的样本子集L={l1,…,lj,…,lb},组成一个Batch。 步骤3:对L中每一个样本点lj,计算其与k个簇类中心的相似度,将样本点lj划入相似度最大的簇。 步骤4:L中所有样本经过步骤3后,根据各样本的簇标号重新计算聚类中心。 步骤5:判断是否满足聚类结束的条件(如达到迭代次数t),若未满足,回到步骤2,否则进入步骤6。 步骤6:对Z中的每个样本点,根据其与k个聚类中心的相似程度,将其划分给相似度最大的簇。 Mini BatchK-Means算法的主要计算量集中在步骤3,即计算每个样本点的相似度并确定归属,其时间复杂度为O(knt)=O(n)。 式(3)中,MIC采用最大熵log2(min(s,t))对互信息进行归一化矫正。当变量取值较少,其数据分布只集中在少量网格中时,式(3)计算的MIC测度往往偏小,而这种取值较少的变量,在航天器遥测领域普遍存在。以量子卫星遥测参数“延时遥控指令数”“注入轨道剩余点数”为例,其取值如图3所示,二者采用式(3)方法计算的MIC值为0.41,而皮尔逊相关系数达到了0.95。 分析MIC取值偏小的原因为:归一化因子采用的最大熵,对应的是特殊的均匀分布,而不是变量的实际分布。本文以信息熵代替原有最大熵,作为归一化因子对互信息进行矫正,如式(7)所示,式中变量分布对分子、分母具有等同的贡献而被相互约减,可有效降低变量分布对MIC测度的影响。其中Q为X方向的s段划分,P为Y方向的t段划分。 (7) (a) 遥测时间序列(a) Time series of telemetry (b) 二维遥测分布(b) Two-dimensional telemetry distribution图3 数据分布集中在少量网格Fig.3 Data is concentrated in a small number of grids 3.2.1 相关定义 传统Mini BatchK-Means算法的初始聚类中心是随机选择的,聚类结果具有不可预见性[18]。本文定义4、5,提出一种依据样本分布选择初始聚类中心的方法。 定义5(初始k个聚类中心)S′={〈Value′i,Count′i〉|i=1,…,m}是一维序列统计信息S按Count的降序排列,则初始k个聚类中心C={c1,…,ck}={Value′1,…,Value′k}。 3.2.2 小批量K均值MIC改进算法(MBKM_MIC) MBKM_MIC由两个阶段组成,如算法1所示,第一阶段(行1~2)获取一维序列的统计信息,并按Count字段降序排列,最频繁的取值将被作为第二阶段初始的聚类中心;第二阶段(行3~8)进行MIC值计算,主要包括3个步骤:①利用Mini BatchK-Means算法将X轴划分为s段、Y轴划分为t段;②计算在s、t划分下的互信息值并进行归一化得到信息系数;③循环①、②遍历st≤B条件下所有划分的信息系数,选择极大值作为MIC值。 算法1 MBKM_MIC算法 算法1调用了算法2~4,描述如下。 算法2 GetStatisticInfo算法 3.2.3 时间复杂度分析 第一阶段完成4个快速排序,时间复杂度为O(4nlog2n);第二阶段中,X、Y方向的划分为Mini BatchK-Means算法,其复杂度为O(n),互信息计算需要遍历所有数据,其复杂度亦为O(n),故第二阶段复杂度为O(3nB)=O(n1.6)。算法总复杂度为O(4nlog2n)+O(n1.6)=O(n1.6)。 算法3 MBKM算法 算法4 MI算法 为验证所提方法的有效性,进行了三组实验。第一组实验采用最大熵、信息熵两种归一化因子对遥测数据进行相关性分析,用于验证信息熵因子对取值较少变量的适用性;第二组实验用于验证MBKM_MIC方法的效能,分析该方法得分与动态规划方法得分的差异,评估所提方法的工程可用性;第三组实验,用于验证MBKM_MIC方法的处理效率,确认该方法对大规模数据相关性分析的适用性。 采用量子卫星遥测数据,对改进前后归一化因子的应用效果进行试验。其中最大熵因子算法采用基于动态规划的ApproxMIC[7]算法,信息熵因子算法是在该算法C语言代码基础上进行的改进。 实验选用3组遥测数据,如表1所示(变量维数为所选时段方差不为0的遥测变量个数)。对每组数据中两两变量的MIC值进行计算,以阈值0.8作为相关性筛选条件。实验中发现的相关关系数量对比如图4所示。 表1 三组量子卫星数据 图4 两种归一化因子发现的相关关系数量Fig.4 Number of correlation relationships found by two normalization factors 图4中,采用最大熵和信息熵归一化因子发现的相关关系总计分别为259、305组。经核验:①采用最大熵因子发现的相关关系是信息熵发现关系的子集;②同组变量的相关关系,信息熵因子计算的MIC值均高于最大熵因子;③多出的46组相关关系均为变量取值偏少导致最大熵因子下得分较小、信息熵因子下得分较大的案例,以第3.1节中“延时遥控指令数”“注入轨道剩余点数”为例,其信息熵归一化MIC取值达到了0.94。因此,较之最大熵,采用信息熵归一化因子能够发现遥测数据中更为广泛的相关关系,对于取值较少变量的相关性分析,信息熵归一化因子仍具有良好的适用性。 分别采用MBKM_MIC、ApproxMIC方法,对表1中量子卫星遥测数据进行了处理。MBKM_MIC方法的实验参数设置为B=n0.6,time=3,bsize=100;ApproxMIC参数设置为B=n0.6,c=15。 三组数据的处理结果如图5~7所示,图中横轴为三组量子数据中两两组合的变量组索引,图(a)为ApproxMIC计算结果,图(b)为MBKM_MIC方法计算结果,图(c)为两个测度取值的偏差。三组数据两个测度取值的平均绝对误差(假设ApproxMIC方法取值为标准值)分别为0.103、0.035、0.034,两种方法取值趋势基本一致,误差也非常小。 从图5~7可见,部分变量组的MBKM_MIC方法测度取值低于ApproxMIC方法,这是由MBKM_MIC直接网格划分获得测度取值,而ApproxMIC经历了动态规划寻优过程导致的;另有部分变量组的MBKM_MIC取值高于ApproxMIC方法,分析是由二者分别采用信息熵和最大熵作为归一化因子引起的。 (a) ApproxMIC (b) MBKM_MIC (c) ApproxMIC-MBKM_MIC图5 轨道实时包处理结果比较Fig.5 Comparison of real-time orbit package processing results (a) ApproxMIC (b) MBKM_MIC (c) ApproxMIC-MBKM_MIC图6 姿控慢速包处理结果比较Fig.6 Comparison of slow attitude package processing results (a) ApproxMIC (b) MBKM_MIC (c) ApproxMIC-MBKM_MIC图7 平台实时包处理结果比较Fig.7 Comparison of real-time platform package processing results 采用与第4.2节实验相同的参数设置,对三组量子数据的处理时间进行统计,实验共进行了10次,分别对应样本容量n为1024~10 240 ,间隔为1024,性能测试结果如图8所示。 (a) 轨道实时包(a) Real-time orbit package (b) 姿控慢速包(b) Slow attitude package (c) 平台实时包(c) Real-time platform package图8 处理性能比较Fig.8 Comparison of processing performance 由图8可知,对于遥测数据的相关性分析,MBMK_MIC方法的性能普遍优于ApproxMIC,且样本规模越大,性能优势越明显。 遥测数据相关性发现在卫星数据分析、故障诊断中具有关键的“导航”作用。从高维的航天器遥测数据中挖掘出具有可解释性的相关性知识,可以快捷、高效地发现星载设备间内在的关联关系。本文针对MIC方法应用于大规模遥测数据相关性分析过程中,处理性能较低、偏向于多值变量的问题,提出了改进归一化因子、以Mini BatchK-Means聚类为前驱过程的改进MIC方法。试验结果表明,改进的归一化因子方法对取值较少的变量也具有良好的适用性;改进的MIC方法,在计算结果与ApproxMIC测度偏差可承受的前提下,显著提升了数据处理的性能,是一种适用于大规模遥测数据相关性分析的有效方法。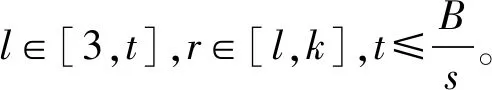
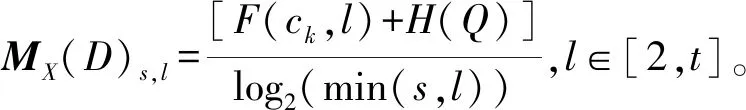
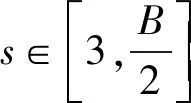
2 Mini Batch K-Means算法
3 改进算法
3.1 改进的归一化因子
3.2 改进的MIC算法
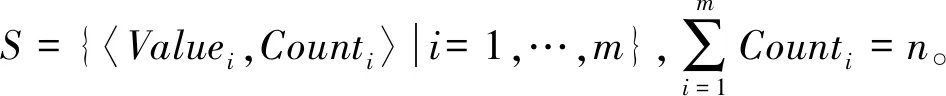




4 实验结果与分析
4.1 改进的归一化因子实验验证
4.2 MBKM_MIC算法效能实验验证

4.3 MBKM_MIC算法效率实验验证
5 结论
