驱动桥总成刚柔耦合建模与试验研究*
2019-10-10史文库刘国政张恒海陈志勇
时 辉,史文库,刘国政,张恒海,3,陈志勇
(1.吉林大学汽车工程学院,汽车仿真与控制国家重点实验室,长春 130022; 2.上海大众汽车有限公司,上海 201805;3.山东交通学院汽车工程学院,济南 250357)
前言
驱动桥是汽车传动系的重要组成部分,也是汽车振动噪声的重要来源,尤其是在汽车加速和滑行时,驱动桥有时会产生令人烦躁的齿轮啸叫声,对于电动汽车尤为严重[1-4]。
对于驱动桥总成的建模,多数文献只考虑驱动桥本体,省略了与驱动桥相连的附属部件:传动轴和钢板弹簧等结构。因为汽车传动系的转矩是通过传动轴传到驱动桥,由于实际安装和使用环境很难满足十字轴万向节的等速条件,传动轴的不等速性必然会对驱动桥动态特性产生影响;钢板弹簧将驱动桥连接在车架上,驱动桥的垂向和纵向运动受到钢板弹簧的限制,在驱动桥有限元建模时需满足板簧座的足够运动空间,尽可能与驱动桥真实装车状态一致,保证仿真结果的正确性。
李专[5]建立了驱动桥的有限元模型,但它只考虑驱动桥本体,且轴承省略了滚子,只保留了内外圈,这必然会带来误差。Choi等[6-7]从准双曲面齿轮啮合激励力出发,分析了驱动桥噪声的影响因素。Xu[8]利用ADAMS软件建立了驱动桥的多体动力学模型,分析了十字轴万向节对驱动桥振动的影响。郭栋[9-10]从声品质角度出发,研究驱动桥的噪声,只建立了驱动桥齿轮的14自由度动力学模型,对于驱动桥系统很难保证精度。卢雷[11]研究了某国产车滑行时的后桥啸叫声,用有限元方法分析了准双曲面齿轮的动态啮合特性,但没有对驱动桥总成进行研究。周驰等[12-13]考虑了轴承刚度耦合性和非线性,建立驱动桥有限元模型,但未考虑传动轴与钢板弹簧等部件。Hua等[14]提出了计算螺旋锥齿轮转子系统有效支承刚度的轴承模型,并比较了不同轴系结构的动态响应。Wang等[15]建立了驱动桥齿轮-轴系耦合的动力学模型,综合考虑了齿轮轴旋转时的陀螺效应,发现齿轮啮合激励是系统动态响应的主要激励源,但陀螺效应对轴承的响应有较大影响,并考察了齿轮转动惯量、齿轮轴刚度和轴承刚度对系统动力响应的影响。Koronias等[16]在ADAMS软件中建立了完整的驱动桥多体动力学模型,虽然在模型中包括了传动轴和钢板弹簧,研究了油温等因素对噪声的影响,但对于复杂的准双曲面齿轮等结构,多体动力学模型很难保证计算精度。
本文中以国产SUV驱动桥为研究对象,在驱动桥总成建模时,综合考虑了传动轴的质量分布、十字轴万向节不等速特性和钢板弹簧的限位作用,保证驱动桥有限元模型更加接近真实的使用状态,最后采用模态试验验证有限元模型的正确性。
1 驱动桥总成结构分析
研究对象是某皮卡车驱动桥,整车采用发动机前置后驱的布置形式,动力总成为四缸直列柴油发动机与5挡手动变速器,具体参数如表1所示。
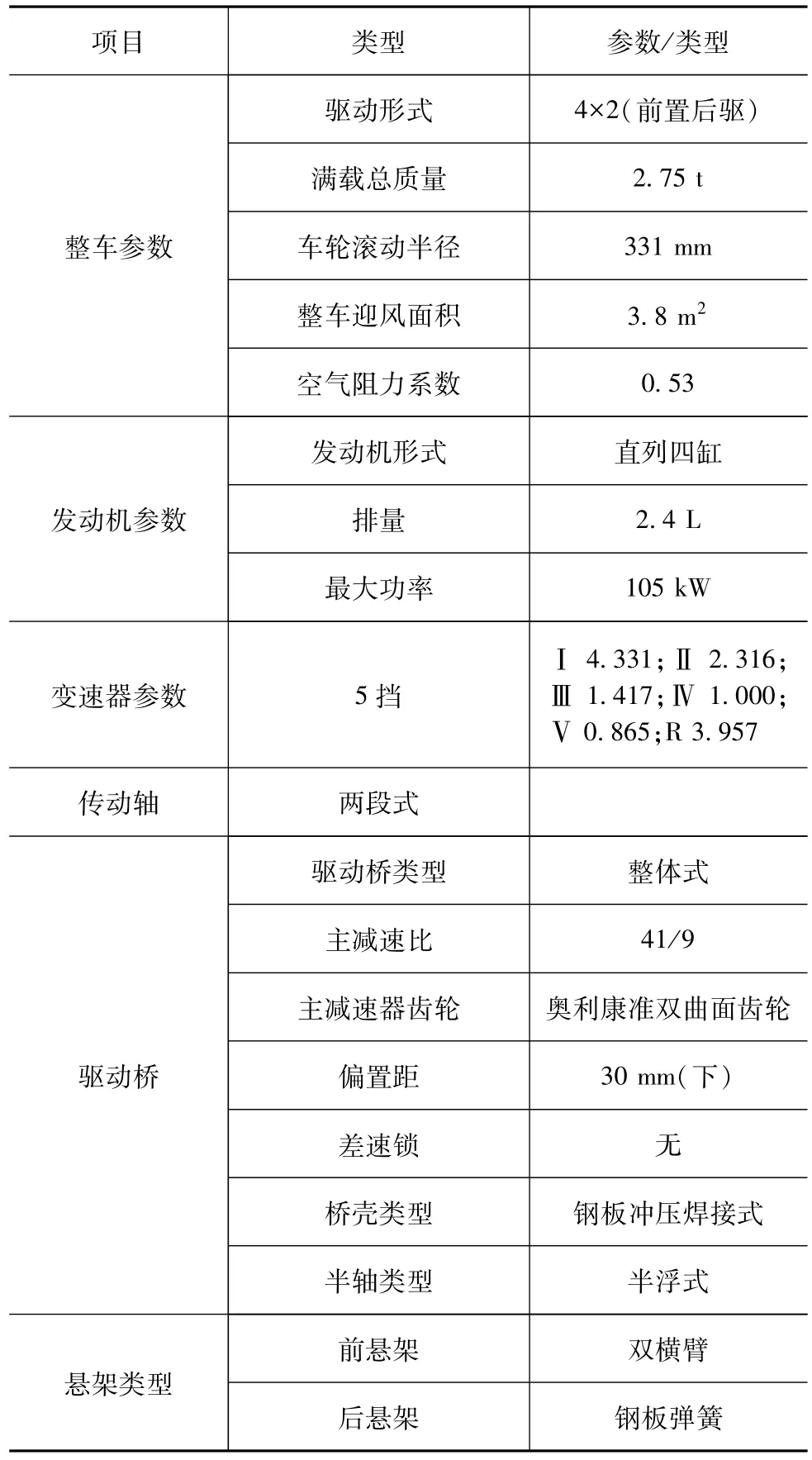
表1 整车参数
驱动桥包括驱动桥总成和附属部件——传动轴和钢板弹簧。首先对模型进行简化,去掉螺母、垫片等细小的零件;然后进行几何清理,便于网格划分;最后将模型导入hypermesh软件中进行网格划分,且检查网格质量是否达到要求。
1.1 驱动桥本体
如图1(a)所示,驱动桥总成一共由100多个零件装配而成,主要包括桥壳、主减速器、差速器和半轴等部件,驱动桥的动力传递路径为:传动轴传来的发动机转矩通过主减速器的主被动准双曲面齿轮传给差速器壳,再通过位于差速器壳内的一字轴传给差速器行星齿轮,差速器行星齿轮与半轴齿轮啮合,将动力通过半轴齿轮的内花键传给半轴,最终将动力传递给车轮。驱动桥总成包括许多细小的部件,包括制动底板、连接螺栓、通气孔和线束安装卡板等,这些小部件不传递载荷,在驱动桥动态仿真中可以忽略。图1(b)为简化后的驱动桥结构。

图1 驱动桥总成结构图
1.2 传动轴
如图2所示,传动轴将发动机的动力传递给驱动桥,传动轴为两段式十字轴万向节结构,传动轴前端与变速器连接,后端与驱动桥相连,中间通过橡胶悬置与车架相连。汽车在行驶过程中,与传动轴前端相连接的变速器基本上不会和车架有相对运动,由于悬架的作用,与传动轴后端相连的驱动桥会与车架发生相对运动,因此,为使该运动不受掣肘,在传动轴的中间位置设计有可轴向伸缩的滑动花键,花键外部装有防尘罩。汽车在行驶过程中,传动轴的转速波动会传递给后桥,给后桥带来新的激励源,因此传动轴在驱动桥建模时不可省略[17]。
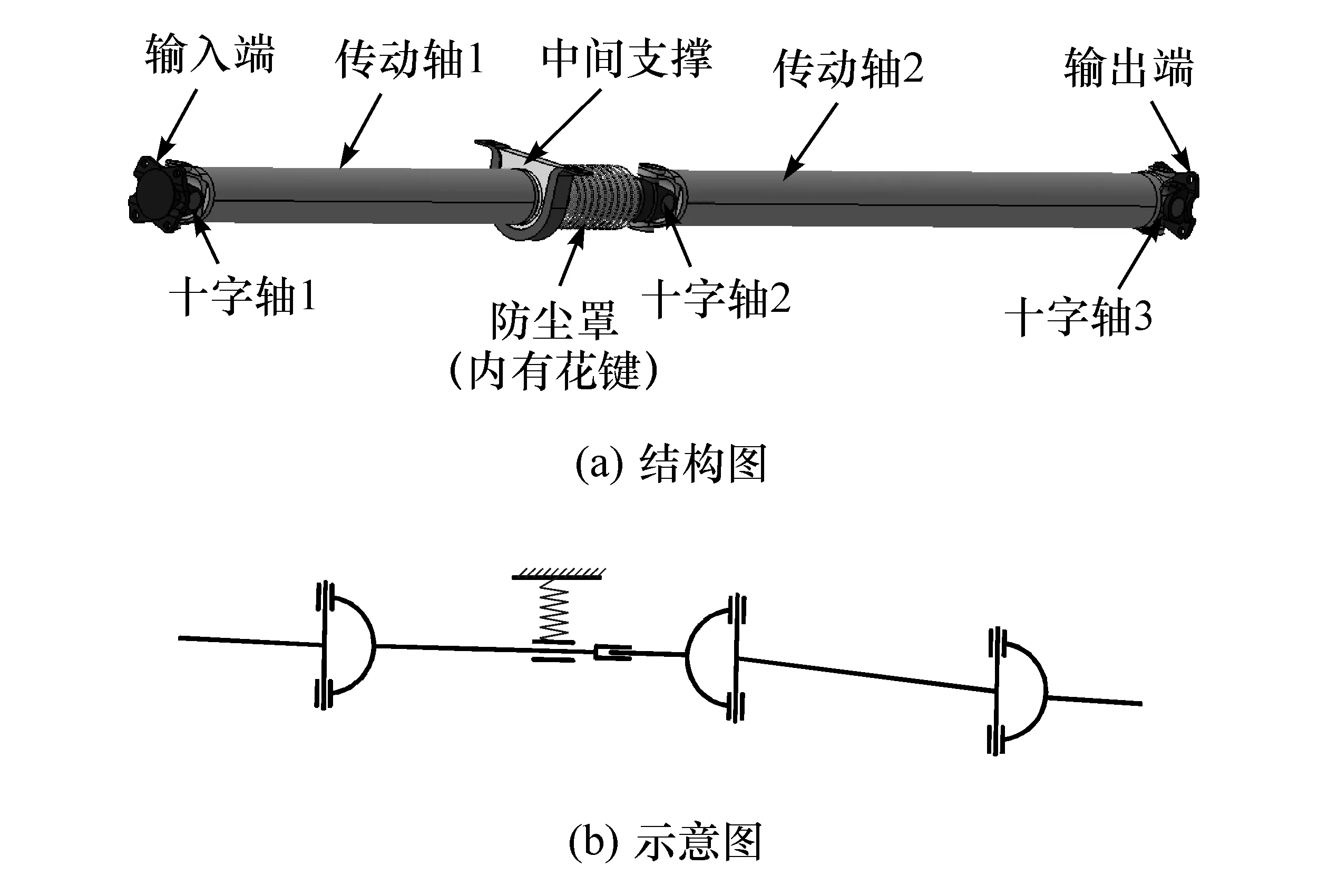
图2 传动轴结构图
简化传动轴的结构,去掉防尘罩、万向节的十字轴、卡环、注油孔等零件,只保留输入法兰、传动轴1、中间支撑、花键、传动轴2和输出法兰等基本结构,十字轴万向节的功能通过有限元软件的连接单元来实现。
1.3 钢板弹簧
图3为简化后的驱动桥整体装配图。钢板弹簧的中部与驱动桥的板簧座相连,前部卷耳和后部包耳与车架相连,同时将驱动桥壳传来的路面载荷传递给车架。由于驱动桥的空间位置受到钢板弹簧的限制,在驱动桥建模时也要考虑钢板弹簧。简化钢板弹簧的结构,去掉卷耳和包耳中的橡胶衬套、U型螺栓和弹簧夹等零件,只保留钢板弹簧本体。为保证各部件安装正确,还须对模型进行运动干涉分析,各个部件之间的螺栓连接和焊接等连接关系在有限元软件中定义。

图3 驱动桥整体装配图
2 驱动桥总成有限元模型的建立
2.1 驱动桥有限元网格划分
驱动桥的实际结构较为复杂,由100多个零件构成,且包括倒角、凸台和小孔等几何结构,网格划分较为困难,且难以保证网格质量。因此,首先在三维绘图软件catia中对模型进行几何清理,去掉对整体结构影响不大的几何细节。再将几何清理后的数学模型以stp格式导入hypermesh软件中进行网格划分。
本文中主要采用六面体和四面体两种单元对驱动桥进行网格划分,六面体单元比四面体单元计算速度更快,且在计算复杂的接触和大变形等非线性问题时更容易收敛。但六面体单元网格划分较困难,四面体网格则较容易,可采用一键生成的方式划分四面体单元。因此根据驱动桥的不同部件的结构,采用不同类型的网格。对于驱动桥主减速器的准双曲面齿轮,由于齿面接触非常不易收敛,对网格质量要求较高,采用C3D8R六面体网格;对于结构复杂的壳体,如桥壳、主减速器壳和差速器壳等,用六面体网格很难划分,因此采用C3D4四面体网格。
齿轮在有限元仿真过程中极易出现不收敛,对网格质量要求较高,尤其是发生接触的齿面网格,准双曲面齿轮用六面体网格划分。由于驱动桥准双曲面齿轮的网格较难划分,因此主要介绍齿轮网格划分的方法。在网格划分时,要保证齿轮的齿面网格密集,以便使齿轮接触过程更易收敛;内部网格稀疏,以便减少网格数量和计算时间。
由于准双曲面齿轮的齿面建模过程非常复杂,因此通过KIMoS设计软件建立并导出准双曲面齿轮的齿面数学模型。图4为主减速器大齿轮网格划分过程,大齿轮一共41个齿,为减少工作量,从大齿轮上切出一个齿,单独对一个齿划分网格,然后通过旋转生成整个大齿轮的三维网格。

图4 大齿轮网格划分
2.2 材料属性定义
驱动桥由许多部件组成,许多部件的材料不同,需要定义不同的材料属性如表2所示。
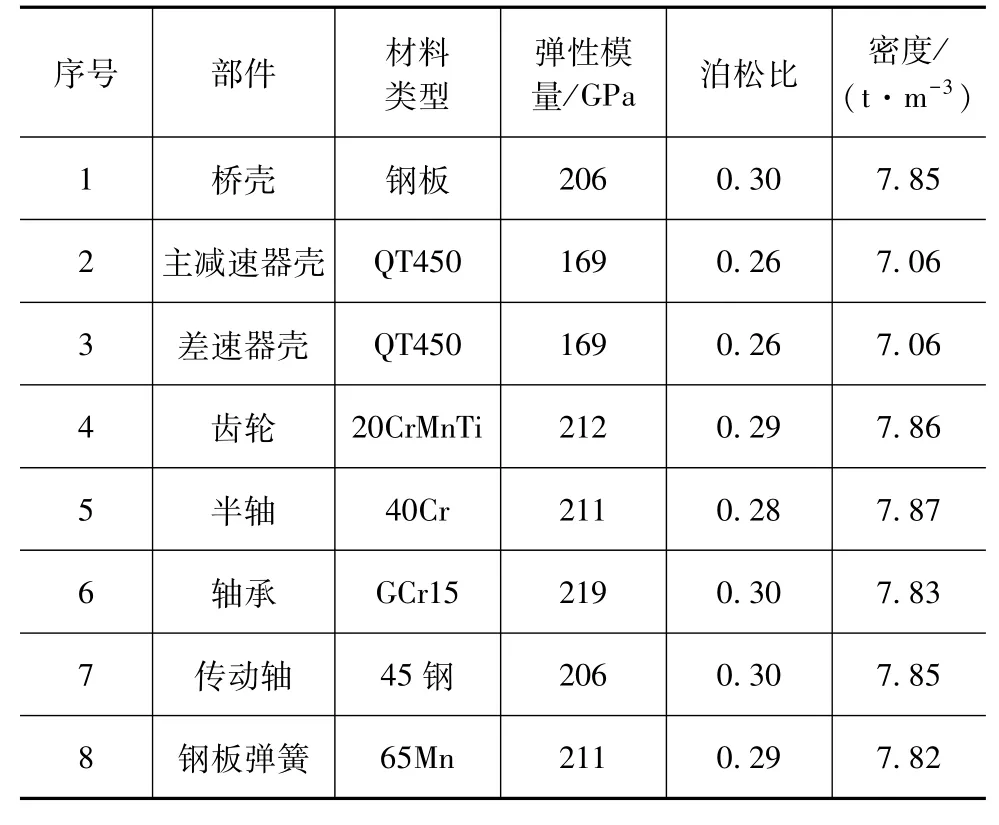
表2 材料属性设置
2.3 设置相互作用
驱动桥由许多零部件装配而成,因此,需要在有限元模型中定义各个部件之间的相互作用,主要包括部件之间的绑定和接触。定义绑定的部件有钢板弹簧与板簧座、传动轴输出端与后桥输入端法兰、主减速器与桥壳、轴承外圈与轴承座、轴承内圈与轴和准双曲面被动齿轮背部与差速器壳等。定义接触的部件有准双曲面主被动齿轮、差速器行星齿轮与半轴齿轮和钢板弹簧的片与片之间等等。
3 驱动桥总成多体连接单元的建立
驱动桥有很多部件之间的连接关系很难通过有限元方法处理,比如传动轴的滑动花键、十字轴万向节和轴承,若都采用有限元方法计算,花键、十字轴和轴承滚子位置需要划分十分密集的网格,且这些部位的接触会导致计算时间过长和不收敛的问题。因此采用ABAQUS中的多体连接单元对这些部位进行建模,这样大大缩短计算时间,且计算过程更容易收敛。
ABAQUS模拟多体系统的步骤是[18]:首先在两个部件上各取一个点(可以是网格节点或者是后建立的参考点),在这两点之间建立连接单元(connector),这样就建立了两个部件之间的联系;再将不同的连接属性(connector section)赋给连接单元,用来描述两个部件之间的相对运动。
常用的连接属性有铰接(hinge)、旋转(rotate)、等速(constant velocity)、十字万向节(U joint)、等速万向节(CV joint)、径向压力(radial-thrust)和轴向滑动(translator)等。
驱动桥有限元模型中,需要建立连接单元的部位分别为:传动轴万向节、传动轴中间支撑、传动轴花键和轴承。驱动桥各个连接单元的属性如表3所示,U1,U2和 U3分别为 x,y和 z方向的平动,UR1,UR2和UR3分别为绕x,y和z轴的转动。
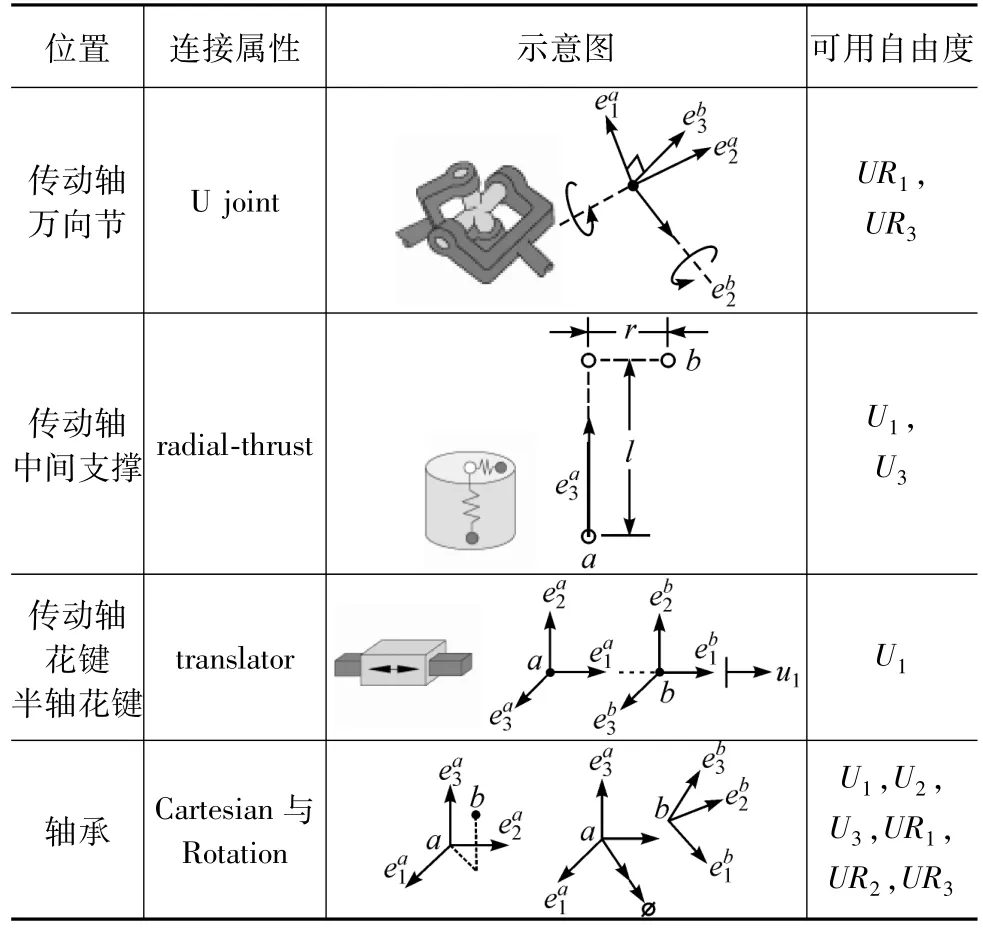
表3 驱动桥各部件的连接属性
3.1 传动轴万向节
采用U joint连接属性来模拟十字轴万向节。如图5所示,在十字轴中心建立两个参考点Node1和Node2,分别与万向节叉的十字轴孔内壁刚性耦合。在两个参考点之间建立连接单元,最后将U joint连接属性赋给这个连接单元,且保证连接单元参考坐标系的y轴与传动轴的轴线重合。
3.2 传动轴中间支撑
采用radial-thrust连接属性来模拟传动轴中间支撑。传动轴中间支撑的弹性元件为橡胶材料,可有效衰减传动轴向车内传递的振动。如图6所示,连接单元的两个节点分别与传动轴外表面和橡胶内表面耦合,且保证连接单元参考坐标系的z轴与传动轴的轴线重合。根据样车的实际结构参数,设置连接单元径向刚度和轴向刚度分别为220和100 N/mm。
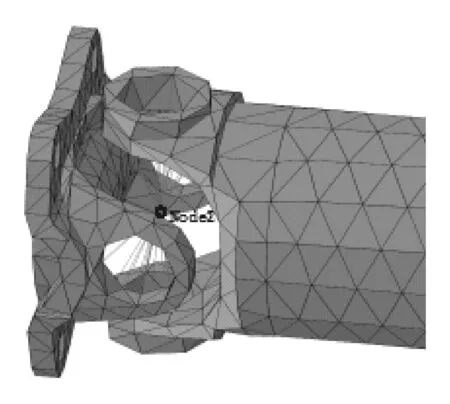
图5 十字轴万向节
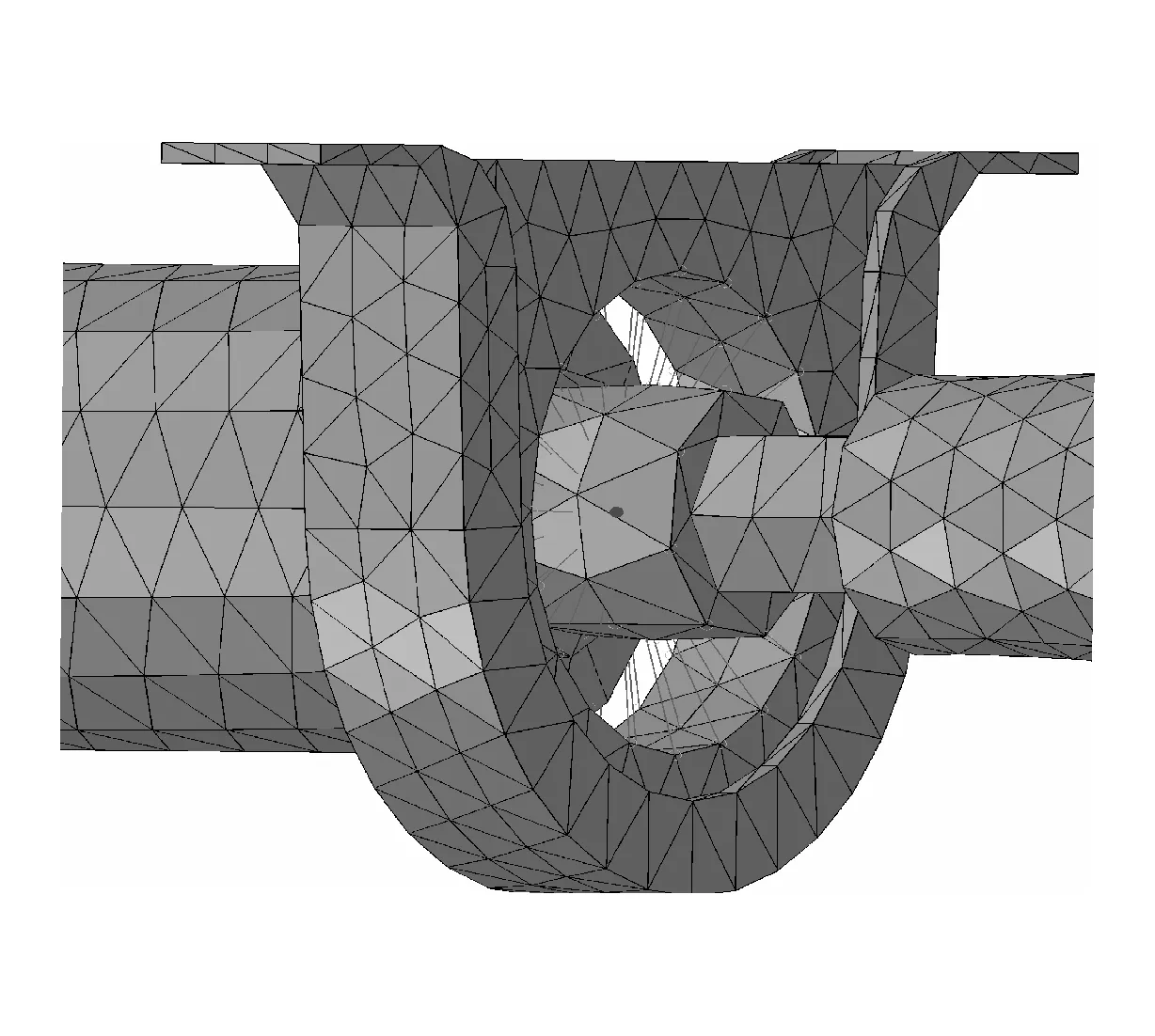
图6 传动轴中间支撑
3.3 传动轴花键和半轴花键
采用translator连接属性来模拟传动轴花键。如图7所示,花键只有沿着轴向的自由度,将连接单元的两个节点分别与内外花键表面耦合在一起,保证连接单元局部坐标系的x轴与花键轴的轴线重合。
3.4 驱动桥圆锥滚子轴承
采用Cartesian与Rotation连接属性来模拟驱动桥圆锥滚子轴承。如图8所示,省略轴承的滚子和保持架等零件,只保留内外圈,轴承连接单元的两个节点位于轴承内圈的中心,两个节点分别与外圈内表面和内圈外表面耦合。轴承除了绕轴线方向外,具有5个方向的刚度(3个平动方向和2个转动方向),同时赋给轴承单元阻尼。
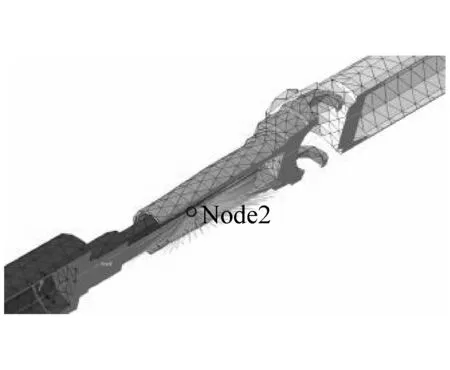
图7 传动轴花键
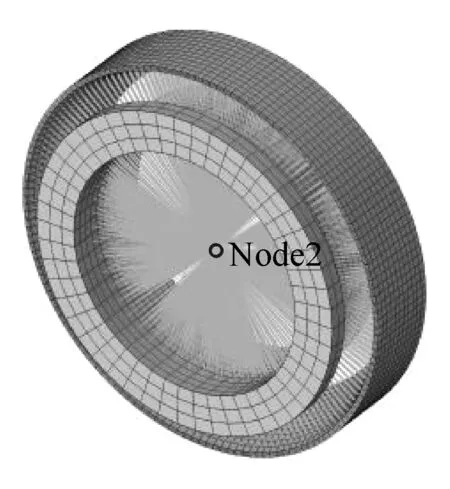
图8 圆锥滚子轴承
4 驱动桥整体刚柔耦合模型的验证
图9为建立的驱动桥刚柔耦合模型。采用模态试验来验证模型的正确性。模态是系统的固有属性,包括模态频率和模态振型,分别取决于多自由度系统振动微分方程的特征值和特征向量。对于线性系统,若其模态已知,则在一定载荷的激励下,系统的振动响应也是一定的,因此可采用模态试验来验证有限元模型的准确性。
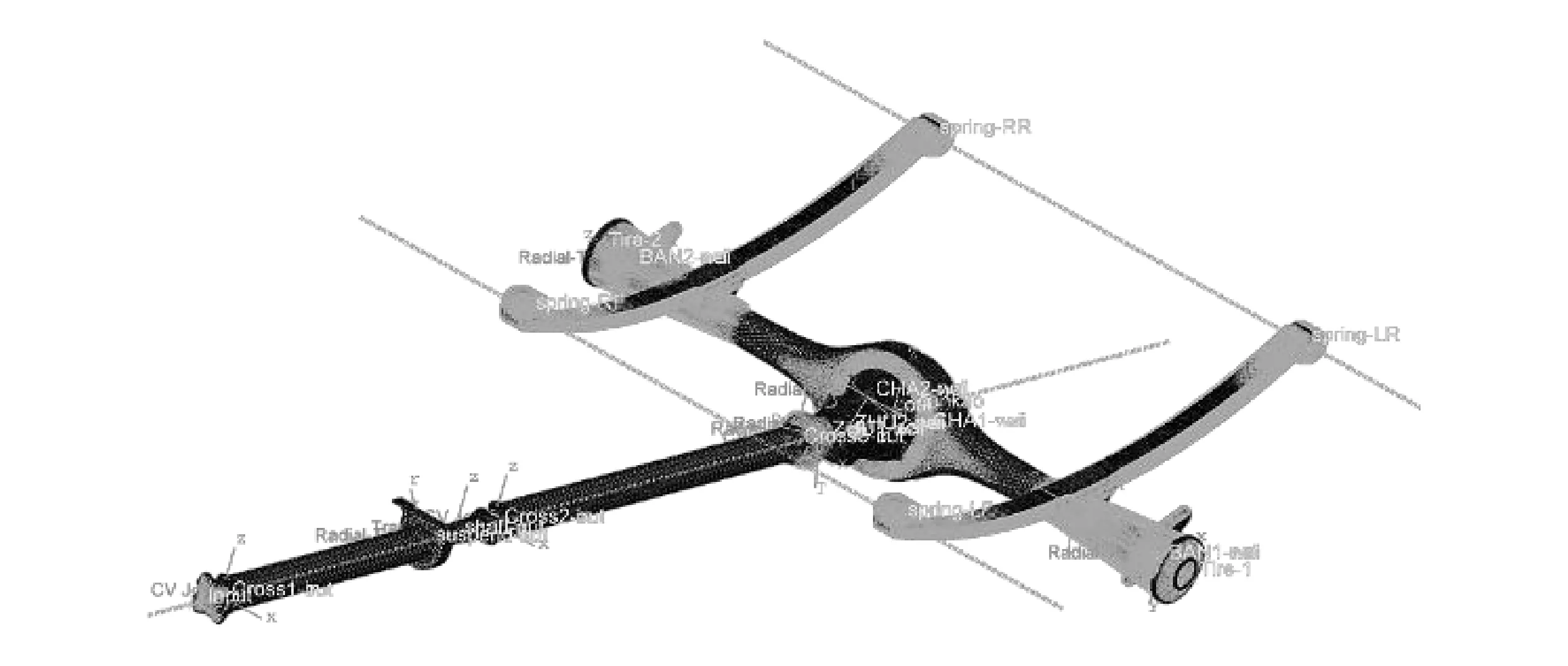
图9 驱动桥刚柔耦合模型
驱动桥模态试验包括自由状态下的模态试验和整车装配状态下的模态试验。前者只考虑驱动桥本体,忽略与驱动桥相连接的其它部件,试验更容易操作,可在室内进行,且驱动桥可视为杆状结构,在自由状态下的驱动桥整体模态振型比较容易辨别,常用第n阶弯曲模态或第n阶扭转模态来描述。但是,由于驱动桥是安装在车上,其运动受到板簧、减振器和车轮的限制,自由状态的驱动桥在实际使用过程中是不存在的,仅仅用来与有限元结果作对比,不能反映真实使用情况。整车装配状态下的模态试验须在整车上进行,以更接近实际使用情况,但是试验操作相对比较困难,且模态与整车状态有关(载荷和胎压等),模态振型不易辨别和描述。
4.1 自由状态的驱动桥模态试验
模态试验通过对结构施加一定的动态载荷,采集各个响应点的振动响应和激励点的力信号而获得各个激励点与响应点之间的频响函数,从而求得系统的模态参数。模态试验方法主要有3种:单输入单输出(SISO)、单输入多输出(SIMO)和多输入多输出(MIMO)。常用的激励方法有激振器激励和力锤激励,前者适用于体积较大的部件或非线性较强的结构,通过扫频激励获得系统的模态参数,需要用到信号发生器、功率放大器和力传感器等,操作较复杂;后者是用力锤给系统一个脉冲激励,相对比较简单。本文中驱动桥模态采用单输入多输出(SIMO)的锤击法测量。试验所用的传感器主要包括力锤(图10)和振动加速度传感器(图11)。

图10 力锤

图11 振动传感器
图12 为驱动桥自由状态下的模态试验。用3根串联弹簧的绳子将驱动桥悬挂起来,绳子分别绑在驱动桥两端的半轴处和主减速器的输入轴法兰处,这样驱动桥和绳索可以等效为一个单自由度振动系统:忽略绳索的质量,驱动桥可视为一个质量点M,绳索和弹簧提供刚度K,则系统的固有圆频率为。为使整个系统的刚体模态和驱动桥的结构模态充分分离,一般要保证驱动桥的最低阶结构模态频率和刚体模态频率至少相差10倍,驱动桥1阶弯曲模态频率一般在50 Hz以上,因此要求10π。驱动桥自由状态模态试验中采用力锤激励,锤头有橡胶、塑料和金属3种材料可供选择,分别在低频、中频和高频处获得较好的相干性,本文中研究的驱动桥在1 000 Hz以内的模态频率,在金属锤头激励频率带宽范围内,因此试验时采用金属锤头。选择刚度较大的主减速器壳为锤击点,保证整个结构都能受到激励,且避免锤击点为模态节点位置。力锤的激励信号为脉冲信号,采用一点激振多点采集的方式,一共布置43个拾振点,每个拾振点有3个方向的振动响应,一共需要129个数据采集通道,但是所用的LMS Scadas前端只有72个通道,因此分两次测量,最终汇总得到驱动桥总成的模态。

图12 驱动桥自由状态模态试验
表4为驱动桥自由状态模态仿真与试验结果。模态仿真是在ABAQUS软件中进行,在有限元模型中去掉传动轴和钢板弹簧,只保留驱动桥,采用兰索斯(Lanczos)迭代法[18]计算驱动桥的模态。从表中可看出,驱动桥仿真模态和试验模态的振型一致,各模态频率的误差在5%以内,说明有限元模型是准确的。

表4 自由状态的驱动桥模态仿真与试验结果对比
4.2 整车状态的驱动桥模态试验
图13为整车安装状态下的驱动桥模态试验。同样采用单点力锤激励多点响应的方法测试。由于试验现场条件的限制,只在驱动桥表面布置16个拾振点。其中在桥壳两侧各布置4个测点,桥壳中间位置上下各布置3个测点,在主减速器前端和桥壳后盖位置各布置一个测点。这16个测点所构建的驱动桥几何模型如图13(b)所示,保证测点能基本勾勒出驱动桥的外形。
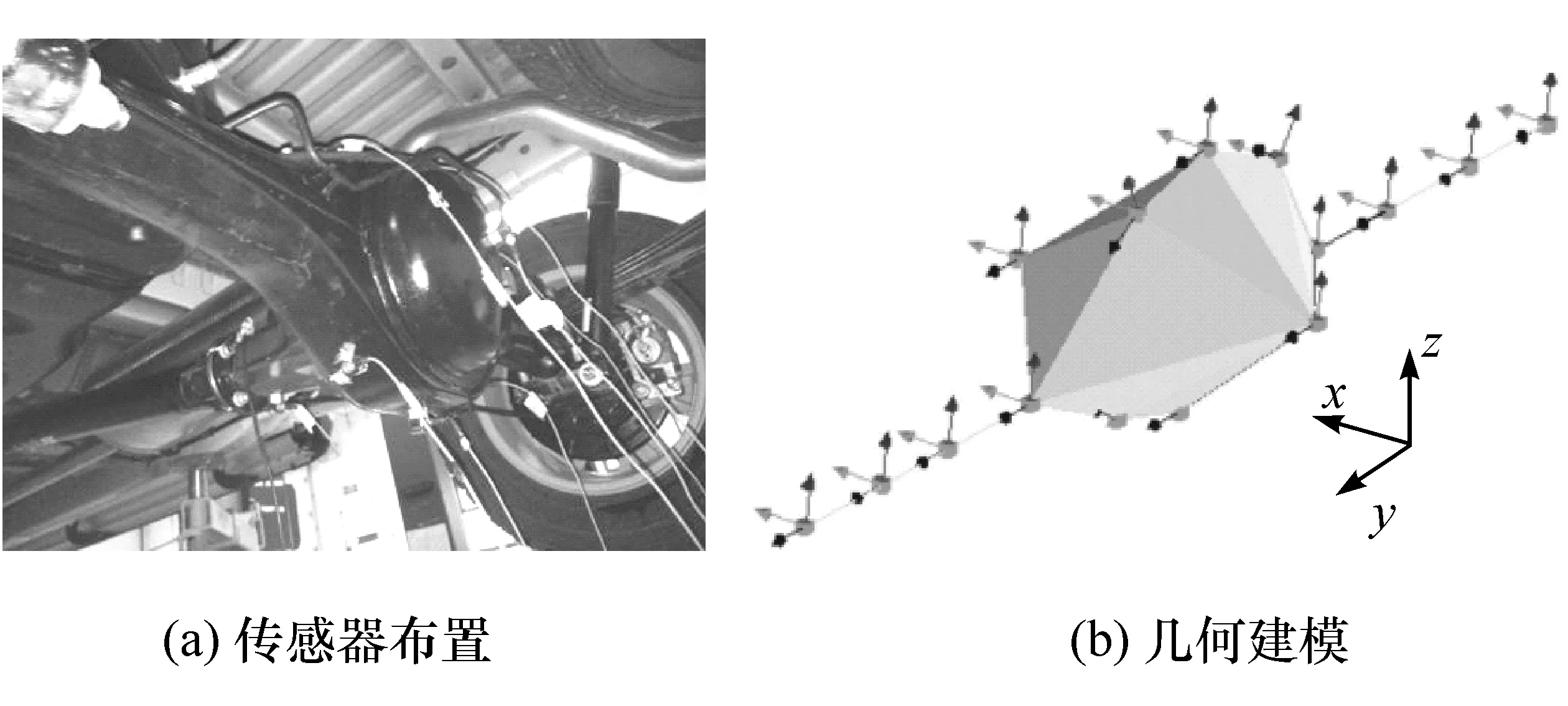
图13 驱动桥安装状态模态试验
整车状态的驱动桥模态仿真,须固定住传动轴悬置位置以及钢板弹簧的卷耳和包耳,在左右两侧车轮施加垂向力,同样采用兰索斯(Lanczos)迭代法计算。表5为试验和仿真结果的对比。由于增加了钢板弹簧和传动轴,驱动桥的等效质量和受到的约束发生改变,整车状态的驱动桥模态与自由状态的驱动桥存在很大的差异,前者的弯曲模态频率较低;整车状态的驱动桥模态还存在整体侧向平动和整体俯仰运动两个模态,与钢板弹簧的刚度有关;对于仿真和试验之间模态频率的误差,整车状态要明显大于自由状态,与模型忽略了轮胎、减振器和横向稳定杆等驱动桥的附属结构有关,但是整车状态的模态频率误差仍在7%以内,且仿真和试验的模态振型一致,说明驱动桥刚柔耦合模型是准确的,可用来进一步仿真分析驱动桥的动态特性。
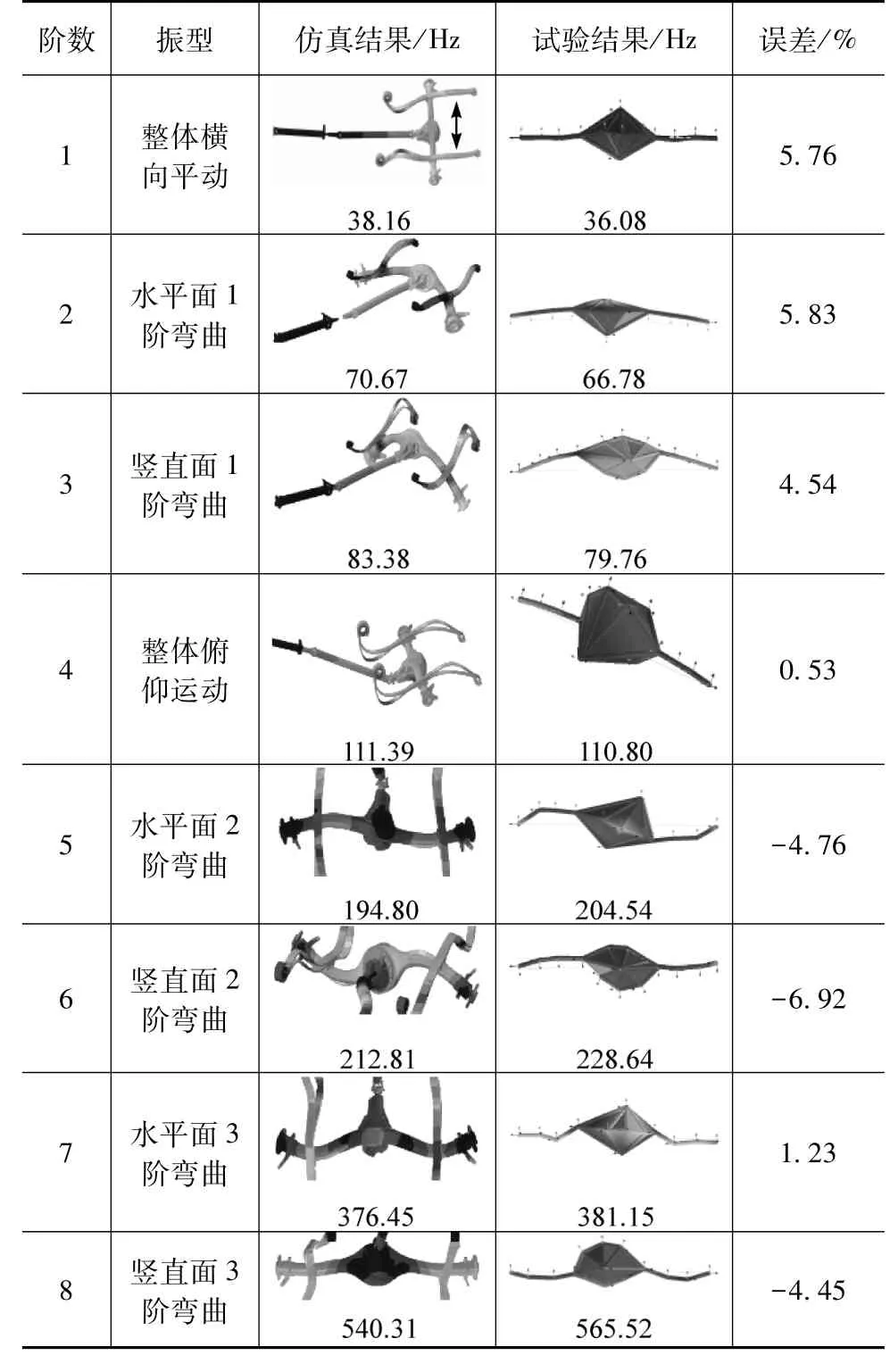
表5 整车状态的驱动桥模态仿真与试验结果对比
5 结论
完善了驱动桥总成的刚柔耦合建模和试验方法,建立了完整的驱动桥模型,综合考虑了传动轴和钢板弹簧等连接部件。齿轮、桥壳和半轴等部件采用有限元建模,轴承和花键等部件采用多体连接单元建模,在保证计算精度的前提下提高了计算速度,主要结论如下。
(1)由于驱动桥轴承和花键等部件结构复杂,采用有限元建模不仅导致网格数量庞大,计算时间过长,还不易收敛,采用多体连接单元可避免此问题。
(2)传动轴将动力传递给驱动桥,钢板弹簧对驱动桥起到固定和限位的作用,建模时这两个结构不可忽略。
(3)驱动桥在自由状态下模态振型不能反映整车安装状态下的模态振型,故不能单独将驱动桥作为研究对象,须综合考虑与之相连接的部件。
(4)驱动桥模态的仿真结果和试验结果基本一致,误差在7%以内,说明驱动桥的刚柔耦合模型是正确的,可用来仿真驱动桥的动态特性。
