基于实车道路数据的插电式混合动力能耗敏感性分析*

2019-10-10夏洪朴吴光耀童荣辉

汽车工程 2019年9期

夏洪朴，王斌，吴光耀，李铁，童荣辉

（1.上海交通大学，船舶海洋工程国家重点实验室，上海 200240； 2.上海汽车集团股份有限公司，上海 200041）

前言

插电式混合动力汽车（plug-in hybrid electric vehicle，PHEV）通过油电混合驱动方式，能够有效降低整车能耗水平。但是，PHEV实车道路行驶时的能耗表现往往都要高于车辆在标准循环工况下的测试结果。因此，探究影响PHEV整车能耗的深层次原因显得极为必要和紧迫。

影响PHEV整车能耗的因素众多，涉及到车辆设计、部件选型、驾驶行为、交通状况和道路条件等各个维度。Sivak等［1］从战略层面（strategic decisions）、战术层面（tactical decisions）和操作层面（operational decisions），详细讨论了车辆选型、路线选择、车辆负载和驾驶行为等因素对车辆实际道路能耗的影响。研究结果表明：选择合适的车型对于能耗具有重要影响，同时驾驶者的操作对于车辆能耗也有45%的降幅。文献［2］和文献［3］中都聚焦于驾驶行为对于整车能耗的影响，并认为不同的驾驶风格将产生极为明显的整车能耗差异，激进的驾驶风格通常与高能耗关联，而保守的驾驶方式则有利于降低整车能量消耗。黄万友等［4］通过试验测试手段研究了车辆加速度、车速、能量回馈、行驶工况和电机过载等因素对纯电驱动汽车能耗的影响规律。试验结果表明：优化后车辆能耗显著降低，有效减小了驾驶员驾驶特性对车辆能耗的影响，与原车相比能耗降低最高可达34.94%。

实际上，影响整车能耗的各相关因素之间存在着强烈的相互耦合关系，必须对这些耦合关系进行必要的解耦处理，否则会影响各相关因素对整车能耗分析结果。因此，本文中基于丰富的实车采集数据进行PHEV整车综合能耗的统计性分析。利用主成分分析方法（principal component analysis，PCA）作为车辆行驶参数的降维解耦工具，并从中提取出关键性特征；采用聚类算法和短行程算法作为构造出恰当的行驶工况，并基于此分析关键性特征与PHEV整车综合能耗的敏感性关系。

1 样本数据

本文中基于上海市嘉定区范围内居民选择测试用户，并分配配置相同的PHEV车辆。车辆详细参数如表1所示。

通过车载无线数据记录仪采集车辆日常行驶数据，采样频率为10 Hz。实车数据采集过程共涉及180人次，累计行驶里程约2 821 km，获得数据集样本量可以确保所收集的车辆行驶信息具有一定的广泛性和代表性。图1所示为实车采集车辆行驶数据的统计结果。PHEV所搭载的12 kW·h三元锂电池，其综合工况纯电续驶里程为60 km，能够满足93.9%的被调查人群出行需求，较为适合上海市居民基本出行需要。

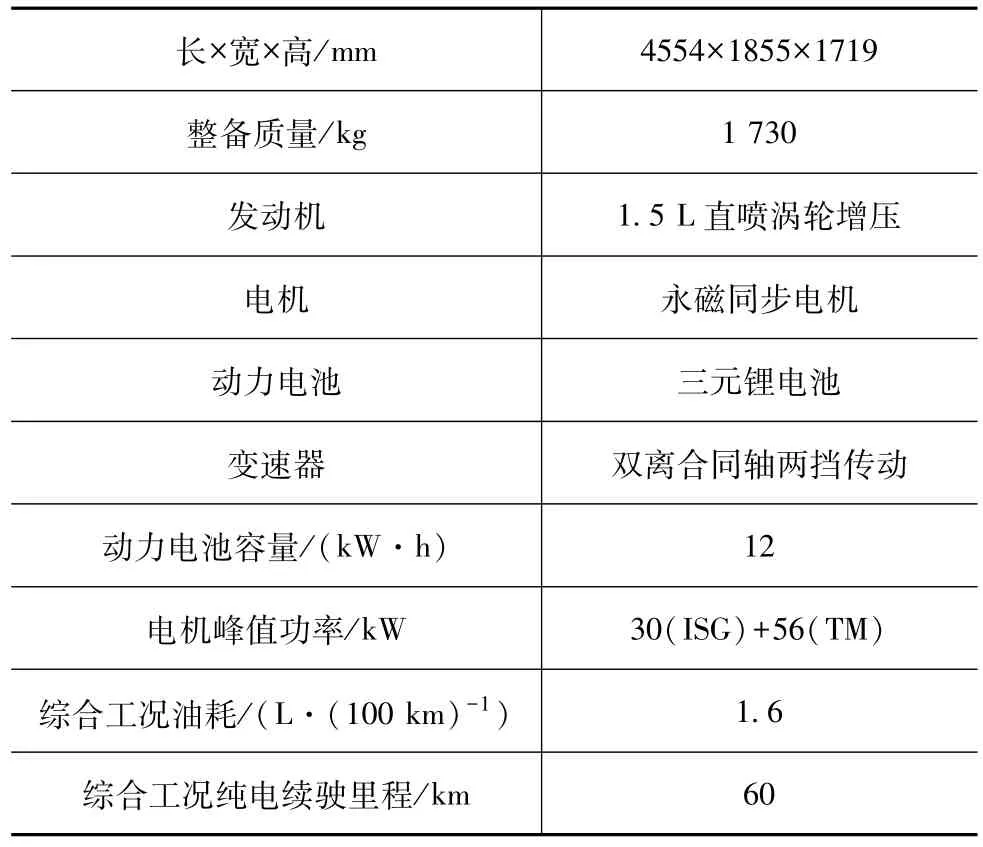
表1 PHEV的基本车辆参数

图1 实车采集样本数据出行状况统计

2 PHEV能耗分析架构与模型构建

本文中所设计的能耗分析架构与基本流程如图2所示。通过对实车采集的车辆行驶数据进行主成分分析，从而找出能够表征车辆行驶过程的关键性特征；由耦合聚类算法与短行程算法生成具有代表性的行驶工况，并通过PHEV整车能量流仿真模型计算出整车能耗水平；使用皮尔逊相关系数法和协方差数值法来综合分析和评价关键性特征对整车能耗的敏感性影响。

图2 PHEV能耗分析架构与分析流程

2.1 样本数据预处理

车辆行程由若干个运动学片段组合而成，因此，需要对所采集的原始样本数据进行运动学片段划分。运动学片段是指：车辆从一个怠速开始到下一个怠速开始的行驶过程［5］。

参考前人的研究成果［6-10］，本文中基于运动学片段对车辆行驶数据进行统计，共涉及21项车辆行驶参数，如表2所示。

为统一PHEV的电能消耗与燃油消耗，本文中通过计算单位里程下整车能耗使用成本Cveh综合评价车辆能耗指标。

表2 基于运动学片段的车辆行驶参数

式中：Cfuel为单位里程下车辆燃油消耗成本（单价为8.9元/L）；Cele为单位里程下车辆电能消耗成本（单价为0.79元/（kW·h））。基于所收集的全部样本数据，本文中整车综合平均能耗使用成本为58元/100 km。

2.2 基于主成分分析算法的特征提取

为从实车采集的车辆行驶数据中提取出表征车辆行驶信息的关键性特征，并消除原有数据间的耦合关系，本文中利用无监督的主成分分析算法对实车采集的车辆行驶数据集进行降维解耦处理，从而获得空间中呈正交分布的若干个主维度向量，即所谓主成分。下面将详细展开论述。

首先，对实车采集到的车辆行驶数据进行Z-score归一化处理［11］，形成数据矩阵D。

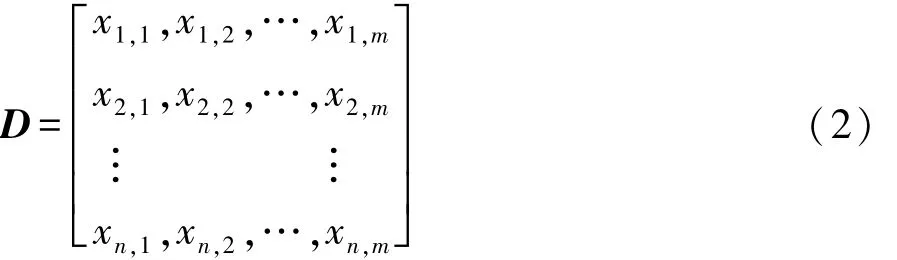
式中：xi，j为归一化后的车辆行驶数据，第i行代表第i个运动学片段，第j列代表第j个车辆行驶参数；n=2767为实车采集数据中整理出来的运动学片段数量；m=21为表2中所列的车辆行驶参数。

然后，计算 D的协方差矩阵 Cov=DDT/（m-1），通过计算协方差矩阵的特征值和特征向量，从而构建出对角矩阵C：

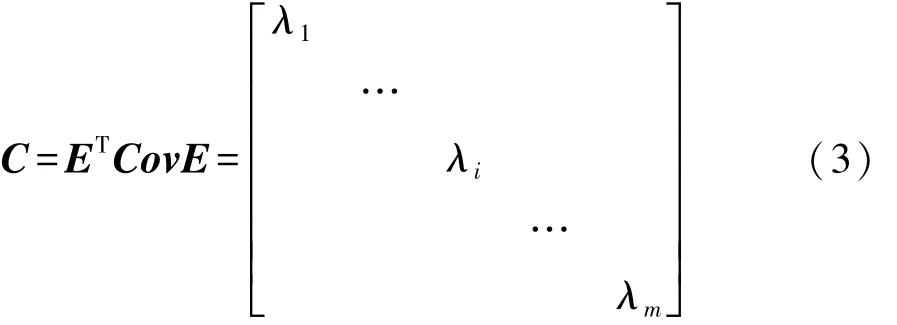
式中特征值λi为第i个主成分Mi的方差，反映了主成分Mi对原始数据集信息量的贡献度，如图3所示。

图3 基于主成分分析算法的信息量贡献度分布

由图可知，前5个主成分对整体信息量的贡献度达84%，说明其是表征车辆行驶信息的关键性特征。

由特征向量ei构成的矩阵E可描述为

其中 ei=［ai，1ai，2… ai，j… ai，21］T

式中ai，j即为车辆行驶参数 j对主成分 Mi的影响系数。

通过对影响系数计算并进行绝对值排序，选出影响该主成分的前4项车辆行驶参数，据此对该主成分进行特征定义，如表3所示。

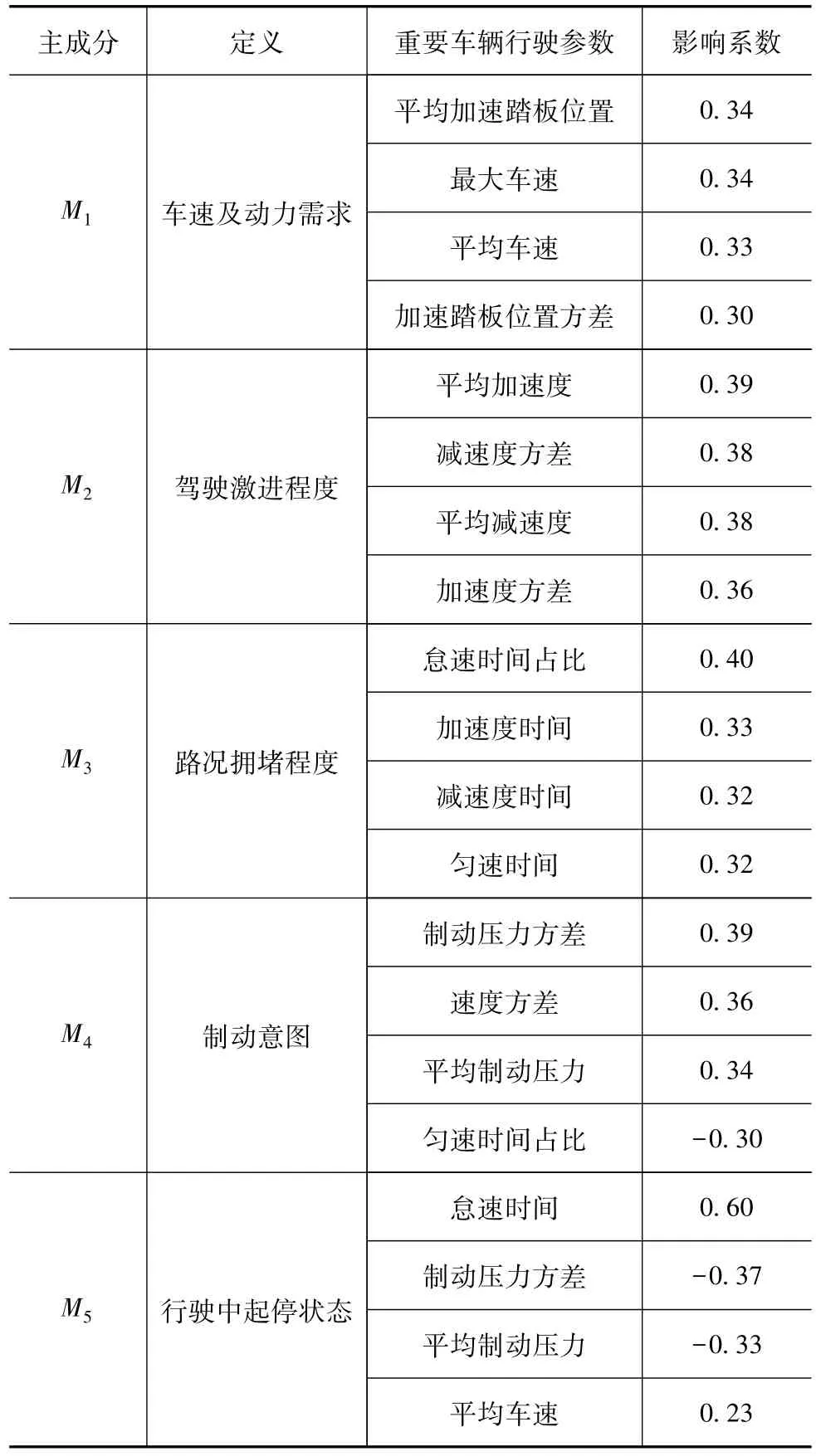
表3 基于影响系数的主成分指标定义

基于运动学片段，根据式（5）可计算得到每个样本的主成分得分。

式中：Pvalue为主成分得分矩阵；Pi，j为第 j个主成分Mj在第i个运动学片段下的得分。

2.3 基于聚类与短行程方法的工况构建与能耗计算

通常，在分析某一主成分对整车能耗影响时，需要对其他主成分进行必要的约束。本文中采用K均值聚类方法［12］，将所有运动学片段聚成k类。在每个类别下，本文中借鉴短行程法片段切割和片段重组的方式来构建新的行驶工况，具体操作方法为：把每个类别中的运动学片段随机组合生成新的行驶工况，为了防止结论存在偶然性，保证结论的全面性，本文中在每个类别下都随机生成10组工况来进行统计分析；然后，根据2.2节中所述方法计算其主成分值；最后，放入仿真模型中计算其能耗值。本文中采用MATLAB/Simulink软件构建了PHEV整车能量流仿真模型，关于模型详细介绍与验证，请参见文献［13］。

本文中综合运用SSE值法和轮廓系数法确定最佳的分类数k。其中，SSE值法通过计算聚类误差来反映聚类效果，如式（6）所示。

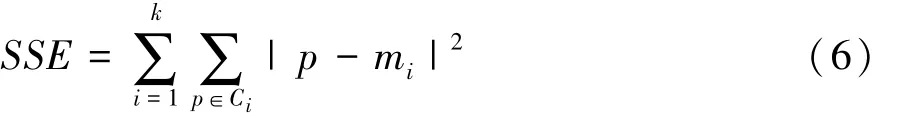
式中：Ci为第i个样本簇；p为样本簇Ci的样本点；mi为样本簇Ci的质心。随着聚类数目k的增加，会导致每个簇的聚合程度不断提高，因此SSE值会逐渐减小，最终收敛至最优聚类数kbest。

轮廓系数法则是通过计算不同簇样本间聚散程度来反映聚类效果，如式（7）所示。

式中：a（i）表示向量i到同一簇内其他点距离的平均值；b（i）表示向量i到最近簇平均距离的最小值。由此可见，轮廓系数 S（i）介于［-1，1］，且越趋近于1代表内聚度和分离度都相对较优。

最近簇的定义如式（8）所示。

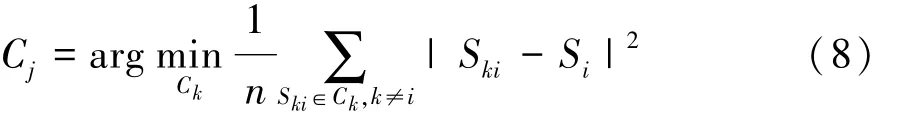
式中Ski为另一个簇Ck中的样本，该式代表样本Si到所有其他簇平均距离的最小值，最小值的那个簇即为最近簇。将所有样本的轮廓系数取平均即得到平均轮廓系数。由此可见，平均轮廓系数越大，代表同簇凝聚越好，簇与簇之间的分离度越好，因此选择平均轮廓系数较大的聚类数k。

图4和图5为选用不同分类数计算得到的SSE值和平均轮廓系数。案例1为研究主成分M1时对主成分M2～M5进行聚类的情况，依次类推。当k=3时，在每个案例下SSE值的变化率分别为（1 711.33，2 837.08，3 311.78，4 454.07，4 532.78），而平均轮廓系数在案例 2，3，4，5都达到了最大值（0.460，0.396，0.396，0.392）。k=4时，SSE值变化率分别为（1 500.55，1 804.59，2 047.95，2 390.04，2 371.73），平均轮廓系数只在案例1中达到最大，然而k=4时SSE都更小。因此，考虑到尽可能使得聚类结果多一些以便分析整车能耗的变化趋势，因此本文中最终选择将聚类数k设置为4。

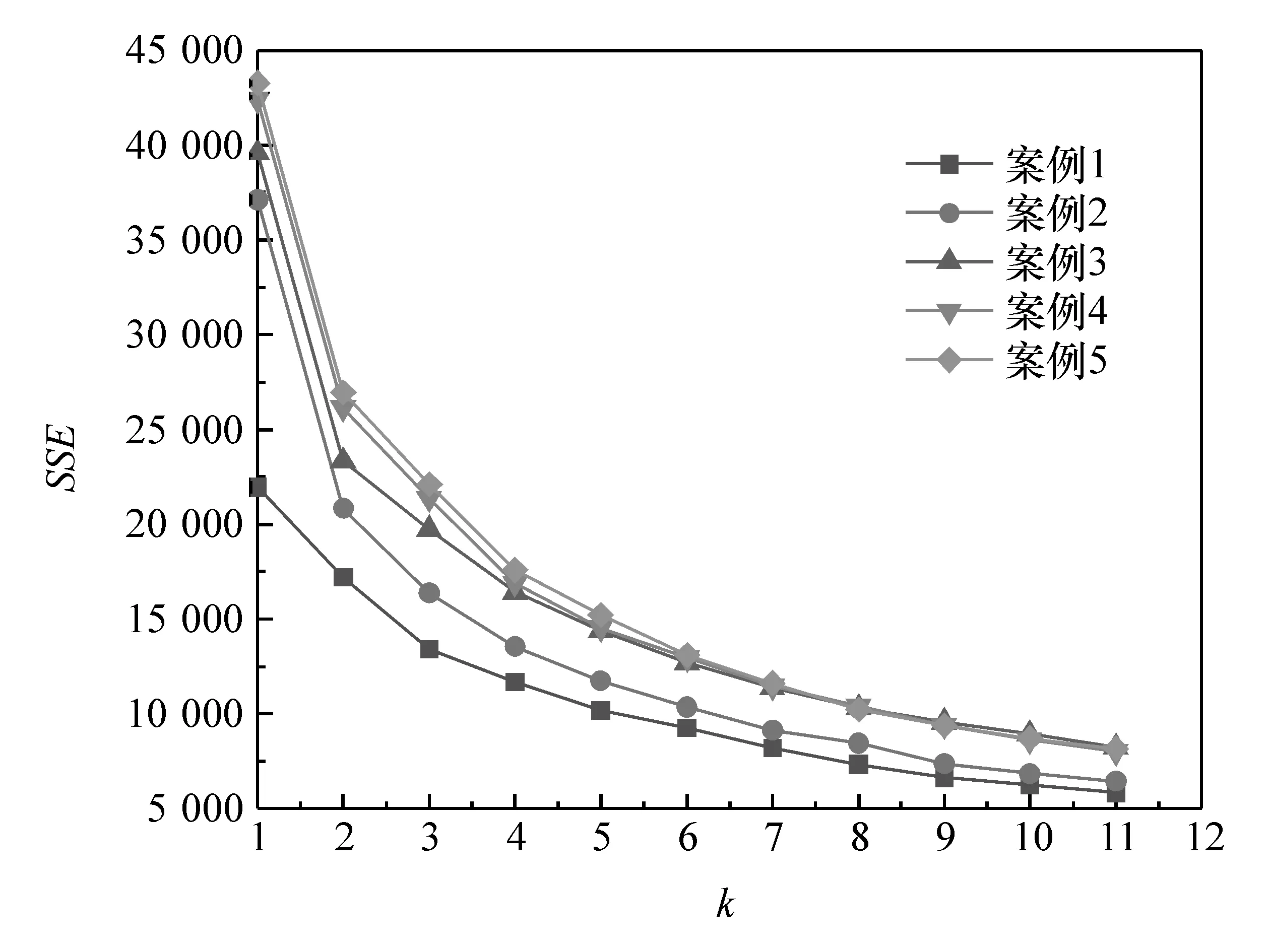
图4 聚类数k对SSE值的影响

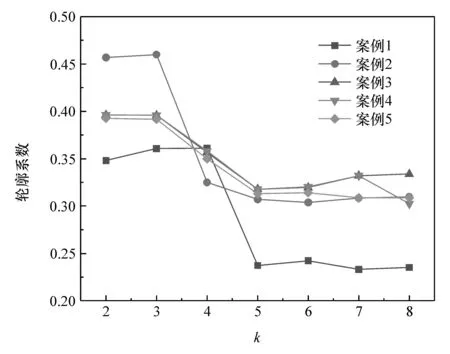
图5 聚类数k对平均轮廓系数值的影响

3 整车能耗敏感性分析

图6所示为主成分M1对PHEV整车能耗的影响，其中，类别1～4代表聚类的4个簇。随着主成分M1的增加，意味着驾驶者对于“车速及动力需求”愈发强烈。由图可知，主成分M1与整车能耗近乎呈线性关系。

不同组的平均能耗值（在图6中以星号标出）随主成分M1的改变而线性变化，即主成分M1与能耗之间具有很强的线性关系。

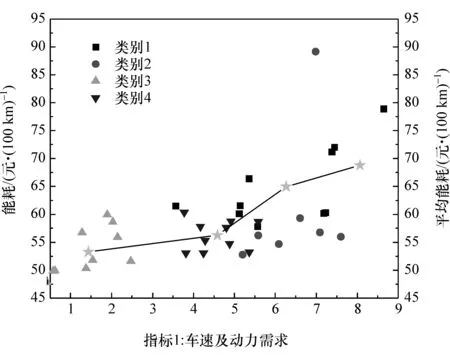
图6 主成分M1对整车能耗的影响

图7 所示为主成分M2对PHEV整车能耗的影响。随着主成分M2的增大，意味着驾驶者“驾驶行为激进程度”不断提升。由图7可知，主成分M2与整车能耗呈现先减少后增加的变化趋势，这是由于随着驾驶行为激进程度增加，意味着加速度和减速度变化更剧烈，即制动踏板和加速踏板更频繁地交换，踏板深度更大。当制动激烈的时候，PHEV会将制动能量用于给电池充电，这对于降低能耗有着很重要的作用，于是会出现先下降的趋势；而当激进程度更大时，能量回馈功能所能发挥的作用不足以抵消发动机频繁变转矩和转速所导致的油耗增加，能耗就会上升。

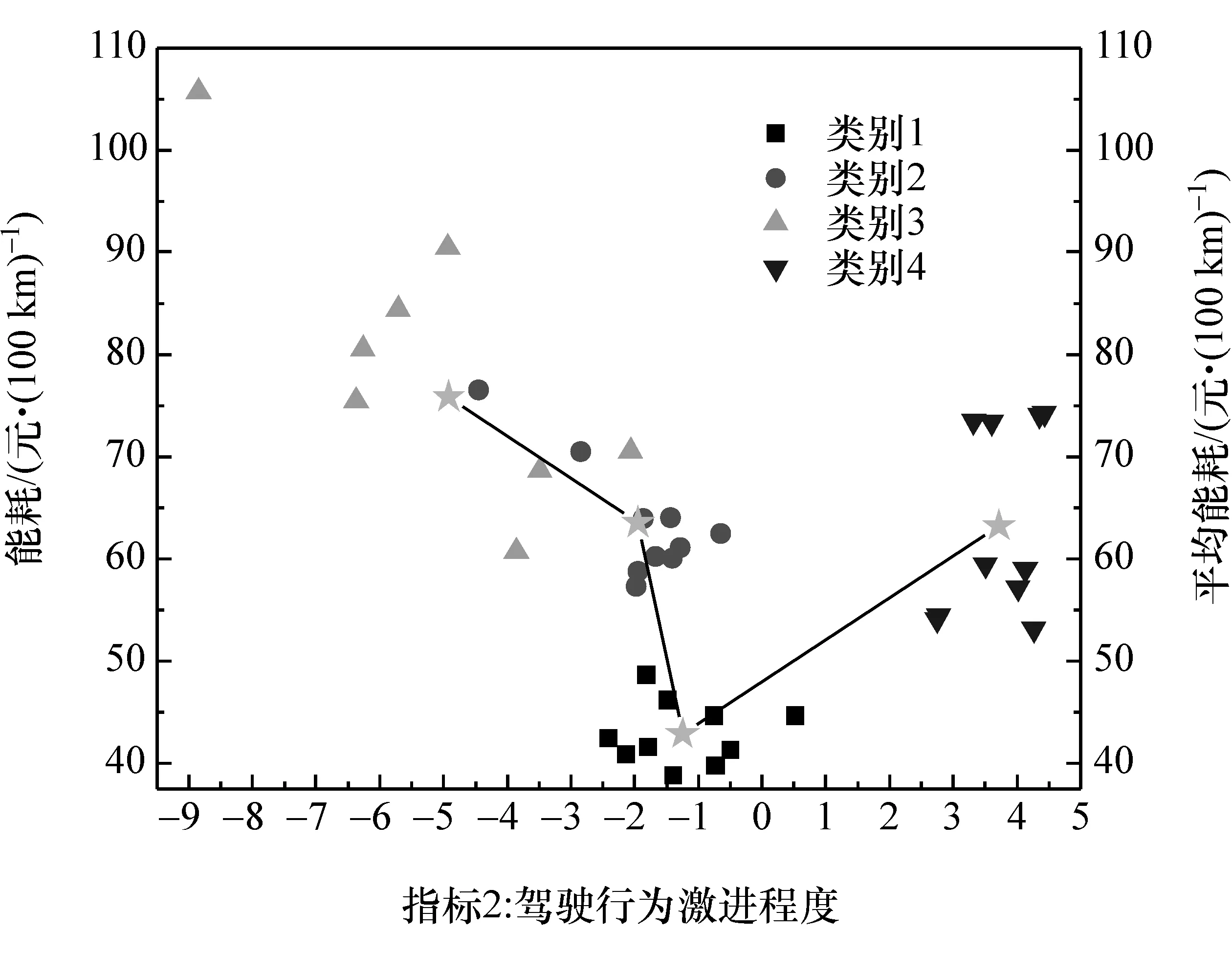
图7 主成分M2对整车能耗的影响

图8 ～图 10分别表示主成分 M3，M4和 M5对PHEV整车能耗的影响。其中，主成分M3反映了“路况拥堵程度”，其与整车能耗呈现非线性的上升关系。主成分M4反映了“制动意图”，其与整车能耗呈现混沌关系。主成分M5反映了“行驶中的起停状态”，其值越大代表车辆怠速时间越长；然而，PHEV车辆在怠速时可以关闭发动机的运行，因此整车能耗较低。

图8 主成分M3对整车能耗的影响

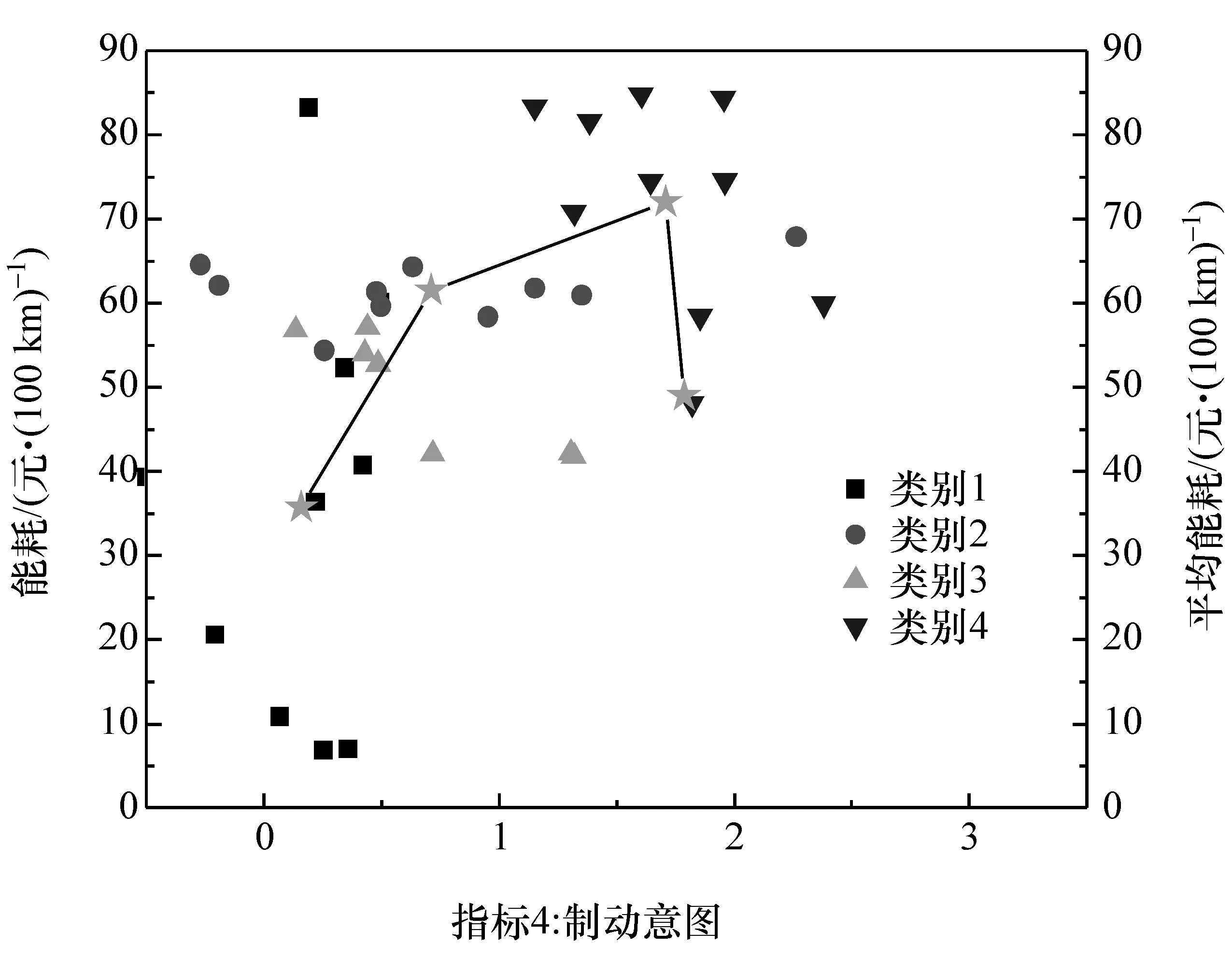
图9 主成分M4对整车能耗的影响

图10 主成分M5对整车能耗的影响

另外，本文中利用皮尔逊相关系数法和协方差法评价主成分与PHEV整车能耗的相互关系。其中，皮尔逊相关系数的计算如式（9）所示。

式中：cov为两个变量之间的协方差；σ为某一变量的方差。

表4所示为各主成分与PHEV整车综合能耗之间的皮尔逊相关系数。每一个案例代表针对某一个主成分的数据分析，表格中的数值代表各项主成分与能耗的线性相关程度。

表4 皮尔逊相关系数法计算结果

由表4中可知，几乎在每一种情况中，主成分M1和主成分M5的皮尔逊相关系数都更大，这表明能耗对“车速及动力需求”和“行驶中的起停状态”这两项指标的线性敏感性更强。另一方面，结合图3的结果：虽然主成分M5占有的信息量只有6%左右，但是其与能耗的线性相关程度与主成分M1的相当（皮尔逊相关系数绝对值平均偏差0.17）。这表明PCA方法得到的主成分对能耗的敏感性，与主成分的信息贡献度并没有必然联系。

但只从线性相关程度并不能全面地表征主成分与能耗的敏感性关系。因此，本文中同时利用协方差法分析不同主成分与PHEV整车综合能耗之间的敏感性关系。协方差法用来表示两个变量有多大程度一同变化，绝对值越大代表一同变化的程度越强。表5给出了不同案例下各主成分与PHEV整车综合能耗之间的协方差数值。由表5中的结果可知：主成分M1在案例1，2，3，5都是绝对值最大值，这表明主成分M1与能耗值敏感性很强；主成分M2在案例4中为绝对值最大值，在案例3和5中都是绝对值次大值，并且主成分M2均为负值，这表明主成分M2与整车能耗呈负相关关系。由此可见，由皮尔逊系数法和协方差法得到的结论有所不同。

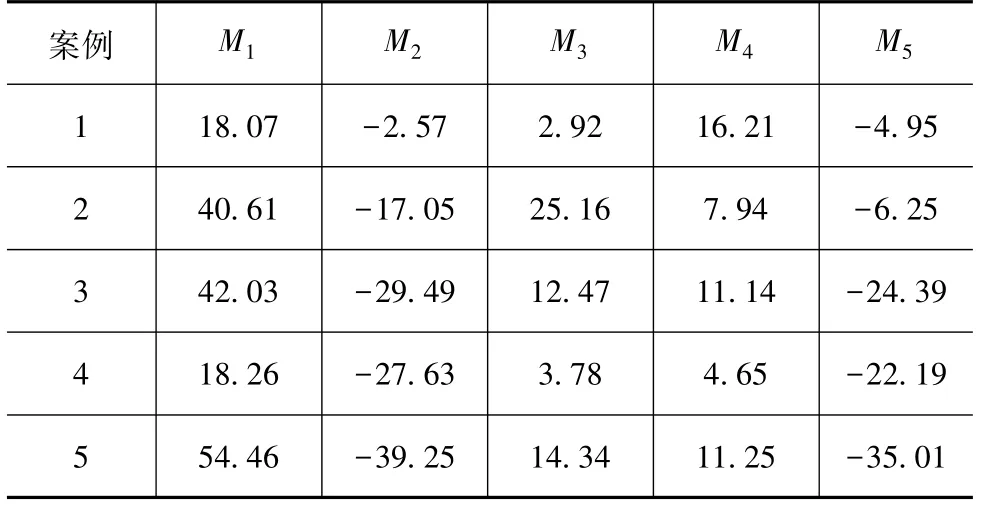
表5 协方差表法计算结果

为全面评价指标敏感性，本文中再次引用聚类算法，根据敏感性分析需求设定敏感性有强弱之分，强敏感性有正负相关之分，以皮尔逊相关系数和协方差值为参数，聚类结果如图11和图12所示。

图11 不同指标协方差和皮尔逊相关系数分布图

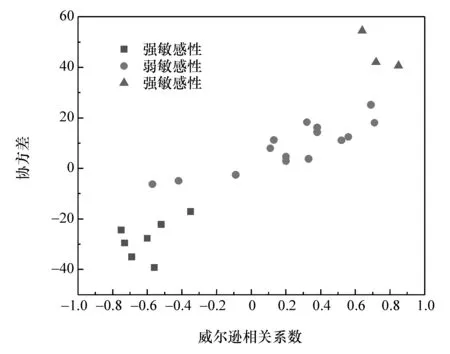
图12 敏感性分析聚类结果

结合图11和图12的结果：主成分M1“车速与动力需求”60%的样本对能耗呈现强正敏感性；主成分M2“驾驶行为激进程度”80%的样本与主成分M5“行驶中的起停状态”60%的样本对能耗呈现强负敏感性；其余主成分均100%的表现出弱敏感性。对图12中不同簇的质心计算得到表6结果，可以根据某一指标的皮尔逊相关系数和协方差值的最近质心类别来定义指标的敏感性强弱。