分布式电动车辆驱动系统MFAC主动容错控制*
2019-10-10江发潮罗禹贡
胡 云,江发潮,陈 锐,罗禹贡
(1.中国农业大学工学院,北京 100083; 2.清华大学车辆与运载学院,北京 100084)
前言
四轮独立驱动的分布式电驱动车辆具有节能且电机冗余的特点,应用日益广泛,其4个电机都能独立控制[1-2],但是电机发生故障时,故障电机无法输出驱动转矩,势必导致车辆出现一系列非期望参数变化,使车身出现失稳的情况,从而增加交通事故发生的概率。但考虑到分布式电驱动车辆4个轮毂电机和转向电机构成系统冗余配置,驱动系统执行器发生故障以后,可以通过驱动系统非故障电机和转向系统的协同控制,实现车辆在驱动系统发生失效以后维持既定轨迹行驶,从而保证驾驶员的安全。
容错控制技术最先是在航空航天领域得到发展,所用到的控制方法包括线性二次控制[3]、滑模控制[4]、控制分配[5]、机器学习[6]等;在车辆容错控制领域,学者对执行器故障诊断以及容错控制策略进行了相关研究,但大部分集中于传统车辆[7]。近年来针对分布式电驱动车辆驱动系统容错控制也有学者进行了相关研究,但大多集中于电机故障诊断以及电机失效控制上。有学者提出同时关闭分布式电驱动车辆失效车轮电机和对侧电机的方法,这样在单个车轮发生故障或者是同轴两个电机故障的情况下能提供部分驱动力且维持车辆稳定性,易于实现,但其没有根据车辆实时状态对车辆车轮转矩进行实时分配,降低了车辆纵向驱动能力[8];清华大学褚文博等[9]针对四轮独立驱动电动车研究了兼顾纵向动力性和横向稳定性的基于规则转矩分配的容错控制策略,但没有考虑部分失效以及其失效后无法进行自适用容错控制;美国俄亥俄州立大学Wang等[10]针对四轮独立电驱动车辆驱动系统容错控制提出了基于自适应的被动容错控制方法和主动故障诊断方法来精确隔离和评估故障,该方法没有考虑不确定性对控制系统带来的影响,并且需要建立复杂的车辆动力学模型。
无模型自适应控制方法是针对离散非线性时间系统使用动态线性化方法及伪偏导数在闭环系统的每个动态工作点建立等价的动态线性化数据模型,然后基于此等价的虚拟数据模型设计控制器并进行控制系统的理论分析[11],实现仅利用被控对象的输入输出信息对非线性系统进行自适应控制。近年来,无模型自适应控制方法已经得到了广泛应用,例如无人驾驶横向控制[12]和自动泊车[13]等。
针对现有的车辆主动容错控制方法大多需要依赖精确车辆模型和故障诊断单元,使得在控制系统设计时由于车辆系统模型复杂、非线性和强耦合等特点带来一系列问题。本文中提出仅利用车辆系统的多个输入输出数据,不包含精确的车辆模型信息,在驱动系统各个失效工况下仅通过驱动系统非故障电机和转向系统自适应协同容错控制,从而保证车辆既能维持期望车速也不偏离既定轨迹行驶,确保行驶安全。
1 主动容错控制系统设计
本文中考虑分布式电驱动车辆驱动系统发生失效以后,基于多输入多输出无模型自适应控制方法,利用驱动系统非故障电机以及转向系统协同容错控制来保证车辆既能维持期望车速前进,也不会偏离既定轨迹。设计的分布式电驱动车辆主动容错控制框架如图1所示,主动容错框架由驾驶员期望模型、MIMO-MFAC控制器和被控对象3部分组成。

图1 MIMO-MFAC主动容错控制系统框图
1.1 驾驶员期望模型
驾驶员期望模型根据期望路径和期望车速通过预瞄PID进行跟踪控制,得到期望的前轮转角,然后根据车辆2自由度模型得到车辆期望的横摆角速度,具体的轨迹跟踪控制逻辑如图2所示。其通过两个增量PID对横向位置偏差和航向角偏差进行控制,将目标轨迹转化为期望前轮转角。

图2 轨迹跟踪逻辑框图
图中,e(y)k为横向位置偏差,e(ψ)k为航向角偏差,δf为前轮转角,xk为后轴中心纵向坐标,yk为后轴中心横向坐标,ψk为航向角
接着将预瞄PID得到期望前轮转角根据式(1)和式(2)所示车辆2自由度微分方程得到车辆期望横摆角速度。
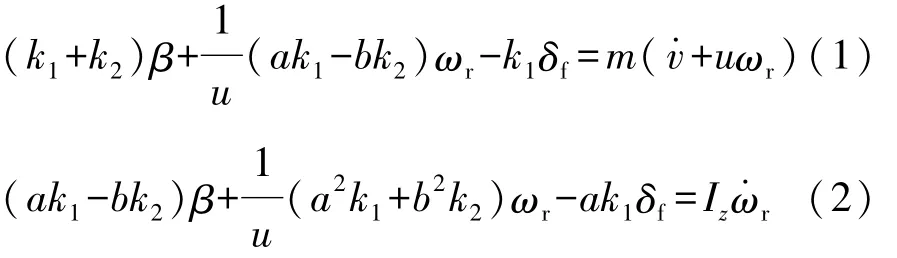
式中:m为整车质量;a为质心到前轴的距离;b为质心到后轴的距离;k1为前轮总侧偏刚度;k2为后轮总侧偏刚度;β为质心的侧偏角;δf为前轮转角;ωr为横摆角速度;u为车辆质心纵向速度;v为车辆质心横向速度;Iz为汽车绕z轴的转动惯量。
1.2 MIMO-MFAC控制系统设计
本文中提出的基于多输入多输出无模型自适应主动容错控制系统的设计不依赖与被控对象精确的车辆模型信息,仅利用系统多个输入输出信息,避免了控制系统设计时由于车辆系统模型复杂、非线性和强耦合等特点带来的问题,参考车辆系统纵向、横向以及横摆动力学模型,结合转向系统以及车轮动力学模型[14-15],确定控制系统输入输出量,输入参数u包含左前轮转矩Tfl、右前轮转矩Tfr、左后轮转矩Trl、右后轮转矩 Trr以及前轮转角 δf,输出参数 y包含左前轮轮速 ωfl、右前轮轮速 ωfr、左后轮轮速ωrl、右后轮轮速ωrr以及横摆角速度 ωr。
MIMO-MFAC主动容错控制器设计首先考虑如下MIMO车辆非线性离散时间系统:

式中:u(k)∈R5,y(k)∈R5分别为 k时刻的系统输入和系统输出;ny,nu为两个未知的整数;f(…)=是非线性函数。
当非线性系统满足如下两个假设时:
① fi(…),i=1,…,m关于第(ny+2)个变量的每个分量都具有连续的偏导数;
②式(3)满足广义Lipschitz条件(利普希茨连续条件),即对任意 k1≠k2,k1,k2≥0和 u(k1)≠u(k2)有:
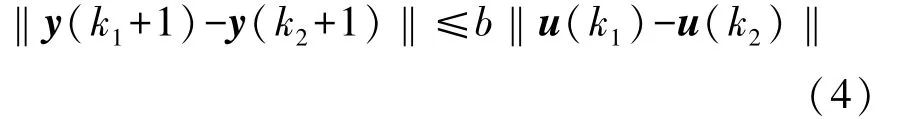
式中b>0是一个常数。
对所有k,当u(k)≠0时,一定存在一个被称为伪偏导数PJM的时变参数Φc(k)使得系统转化为如下紧格式模型:
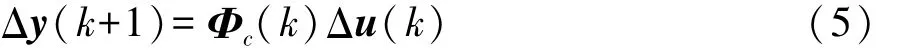

式中Φc(k)为系统的伪雅克比矩阵。
通过算法设计可以得到针对离散时间MIMO非线性系统CFDL-MFAC主动容错控制方案如下:
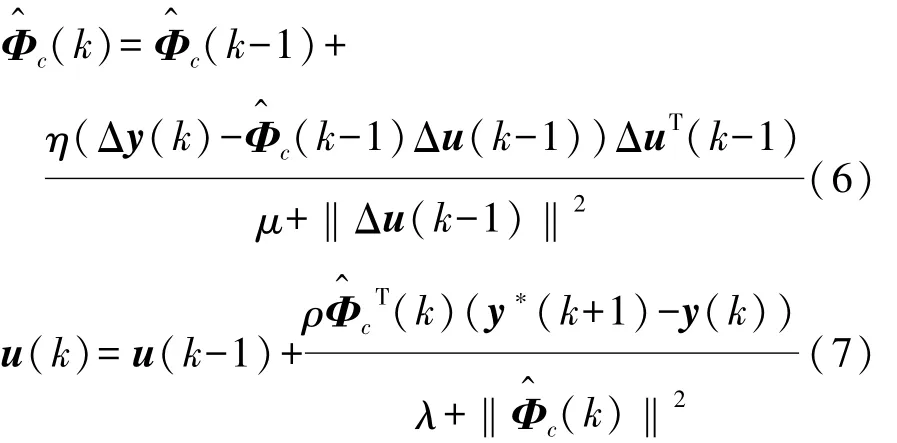
式中:η∈(0,2]为步长因子;μ>0为权重因子;λ>0为惩罚因子;ρ∈(0,1]为步长因子;y*(k+1)为 k+1时刻期望的输出,由系统决定;y(k)为 k时刻的输出。
当分布式电驱动车辆驱动系统发生失效以后,MIMO-MFAC主动容错控制器对车辆姿态进行校正。首先根据车轮驱动转矩 T(.)(k-1)和 T(.)(k-2)、前轮转角 δf(k-1)和 δf(k-2)多个输入数据、实际车轮角速度 ω(.)(k)和 ω(.)(k-1)、实际横摆角速度 ωr(k)和 ωr(k-1)多个输出数据,用式(6)在伪雅克比矩阵 Φc(k)估计器中估算出 Φc(k)。其中 T(.)为车辆左前轮、右前轮、左后轮以及右后轮转矩,ω(.)为车辆左前轮、右前轮、左后轮以及右后轮轮速。
在车辆行驶过程中,不断循环上述步骤,对车辆姿态进行校正,保证车辆维持期望值行驶。
2 稳定性证明
下面对系统的单调收敛性和系统输入输出的有界性进行证明。
(1)单调收敛性证明
定义系统输出误差为

将式(6)和式(7)代入式(8)可得

由矩阵谱半径结论可知,有任意小正数ε1使

式中‖A‖v为矩阵A的相容范数。令d2=1-ρM1+ε1,并在式两边取范数,得
第一,一些企业在编写财务预算管理计划时,常常会出现目光短浅的问题,只看好的当前的利益,没有为企业的长远的发展方向是上考虑。对市场的调研不够全面。这导致了企业虽然近期发展的不错但往后慢慢的被市场所抛弃。因为这种目光短浅的方式,使得企业经受不起市场的突然变动,如果市场的变动过大就可能对企业造成意想不到的打击。
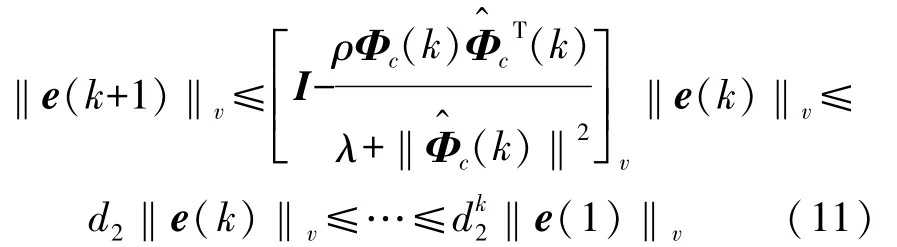
所以系统单调收敛性得到证明。
(2)系统有界输入输出证明
由于y*是给定的常向量,且e(k)有界,因此可得到输出y(k)的有界性。
由于Φ^c(k)是有界的,那么总可以找到一个正数M2,使得下式成立

利用式(7)、式(11)和式(12)可推出
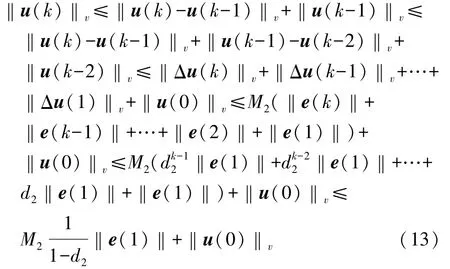
所以控制系统有界输入输出得到证明。
3 仿真与实验验证
对本文中提出的基于MIMO-MFAC主动容错控制方法,进行了MATLAB/Simulink与CarSim联合仿真验证,仿真验证选用CarSim中一辆SUV车辆,其车辆参数如表1所示。另外为了验证算法实时性还选用典型工况进行了驾驶模拟器实验验证,仿真与实验验证均验证了算法有效性。
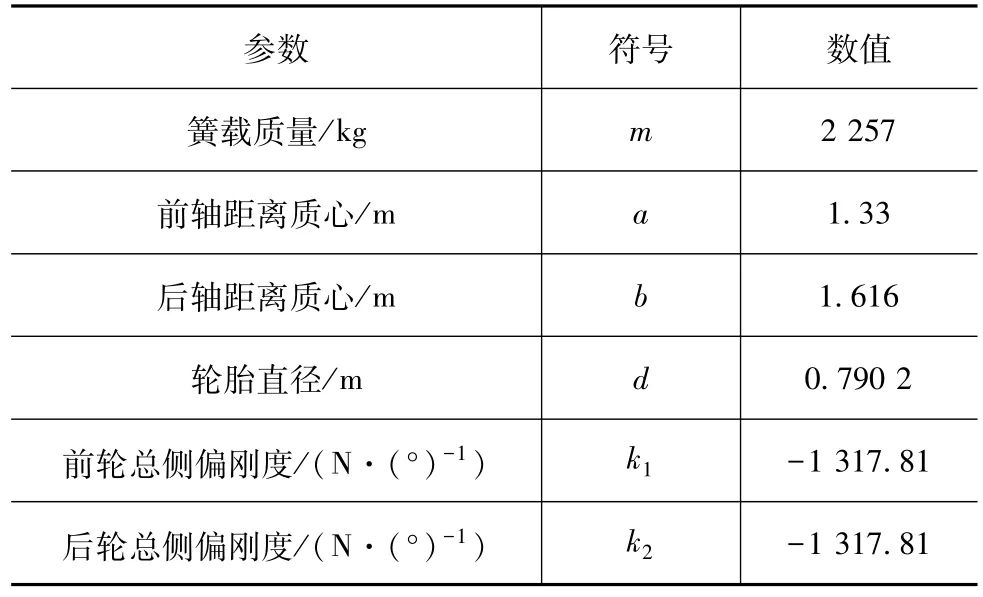
表1 车辆参数
3.1 仿真验证
分布式电驱动车辆驱动系统失效模式可分为单轮失效、异侧双轮失效、同侧双轮失效以及多轮失效,本文中考虑车辆匀速直线行驶和匀速转向行驶两种典型工况。对于分布式电动车辆其同侧电机失效和多电机失效为极限失效工况,如发生必须对车辆采取紧急制动。综上本文中考虑对单个电机失效和异侧电机失效工况采用MIMO-MFAC主动容错控制对车辆姿态进行校正;对驱动系统单轮和异侧双轮所有失效工况均进行了仿真验证,表2~表4分别统计了各失效工况下无控制和容错控制速度最大偏差、横摆角速度最大偏差以及横向位置最大偏差效果对比。结果表明所提出的主动容错控制方法能够保证车辆驱动系统各失效工况下均能按照驾驶员期望车速且不偏离既定轨迹行驶,从而保证行驶安全。
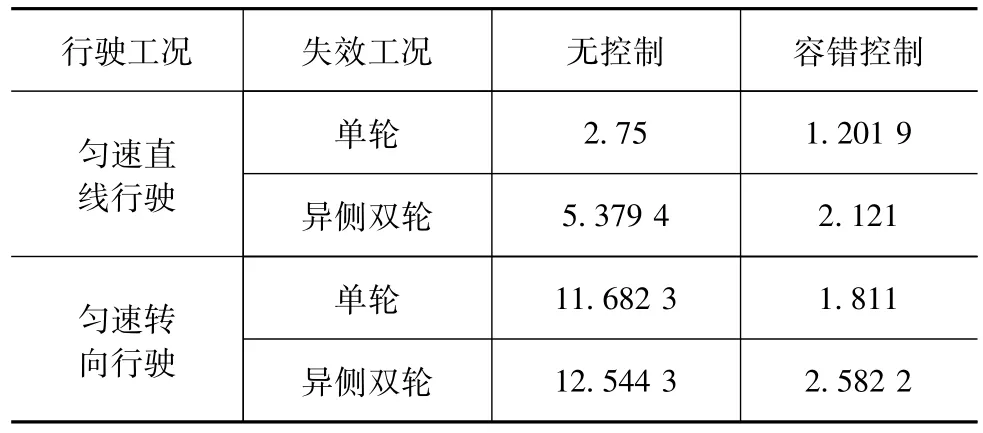
表2 速度有无控制最大偏差 km·h-1
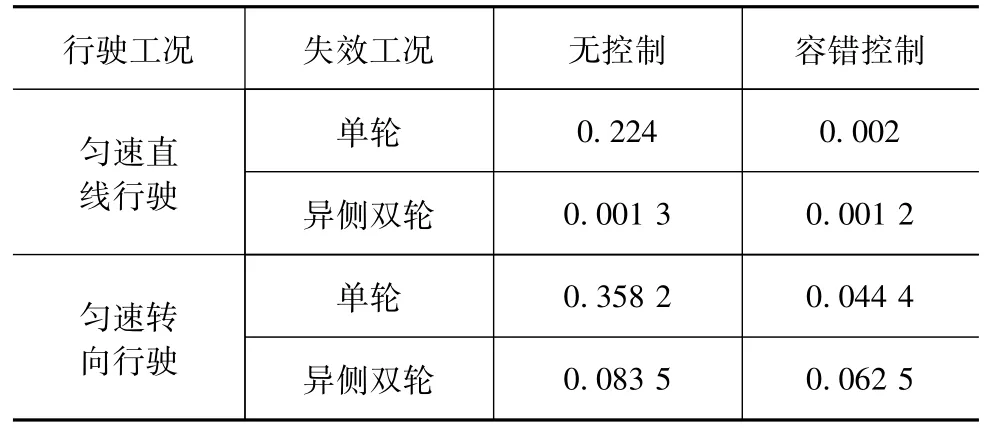
表3 横摆角速度有无控制最大偏差rad·s-1

表4 横向位置有无控制最大偏差 m
下面将详细介绍如表5所示的典型工况下的主动容错控制方法仿真验证分析,仿真结果如图3~图9所示。

表5 仿真验证工况
车辆以72 km/h匀速转弯行驶,如图3所示。由图8可以看出,在左前轮发生失效而没有控制情况下,车辆发生明显跑偏现象,极易诱发交通事故。而在本文中提出MIMO-MFAC主动容错控制算法控制下,左前轮发生失效时,由图4可见,失效有控制时转向盘转角立即响应。与此同时,如图5所示未失效车轮右前以及右后电机转矩降低,左后轮电机转矩增加,从而保证车辆在驱动系统发生失效以后既能维持如图6所示期望车速也不会偏离如图8和图9所示期望轨迹行驶。从图4和图5还可看出,在整个主动容错过程中,随着车轮转矩调节的加入,转向盘转角调节比例在不断减小,从而实现了驱动系统与转向系统的协同容错控制,这种驱动系统与转向系统的协同容错控制方式更加合理,避免执行器发生失效后仅由单个执行器进行校正容易出现过载现象使之无法成功完成容错从而诱发交通事故。表6统计了驱动系统失效后无控制和有容错控制时车速、横摆角速度和横向位置偏差。从表中可以看出,本文中所设计控制器达到了主动容错的目的,且控制效果较好,纵向速度误差维持在3%以内,横向能保证车辆不发生失稳以及跑偏现象,可避免发生严重交通事故。

图3 车辆期望轨迹

图4 转向盘转角
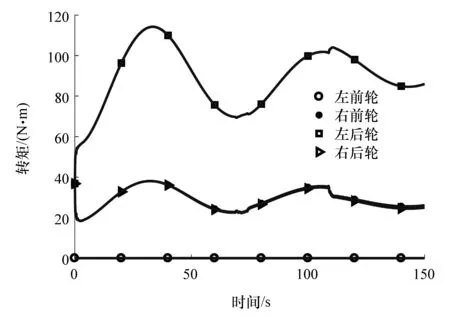
图5 车轮转矩
3.2 驾驶模拟器实验验证
为验证算法实时性,利用图10所示驾驶模拟器平台对表7所示工况进行了实验验证。

图6 车辆速度
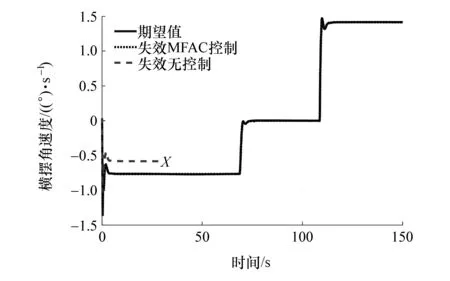
图7 横摆角速度

图8 车辆轨迹
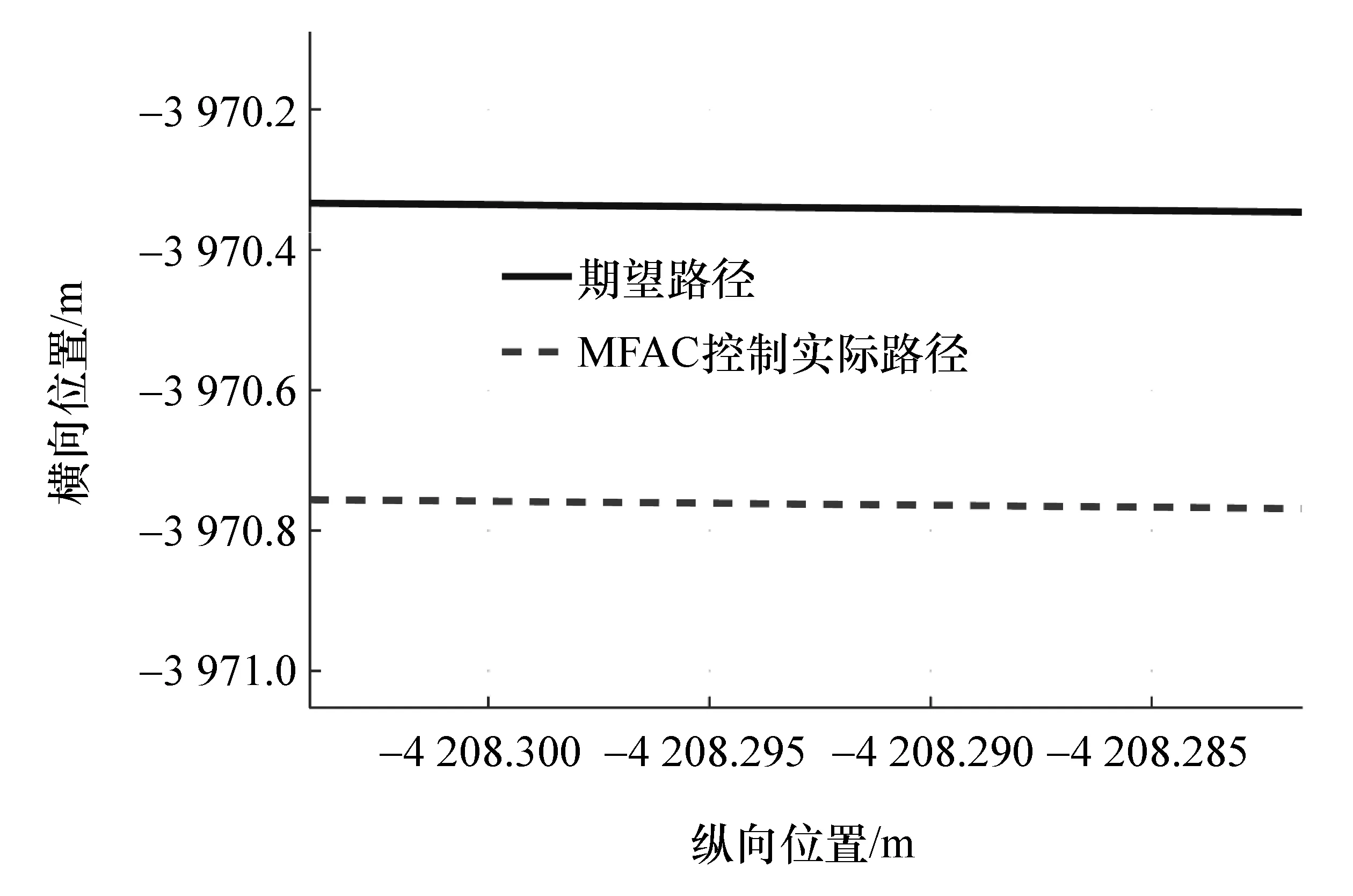
图9 车辆轨迹局部放大图
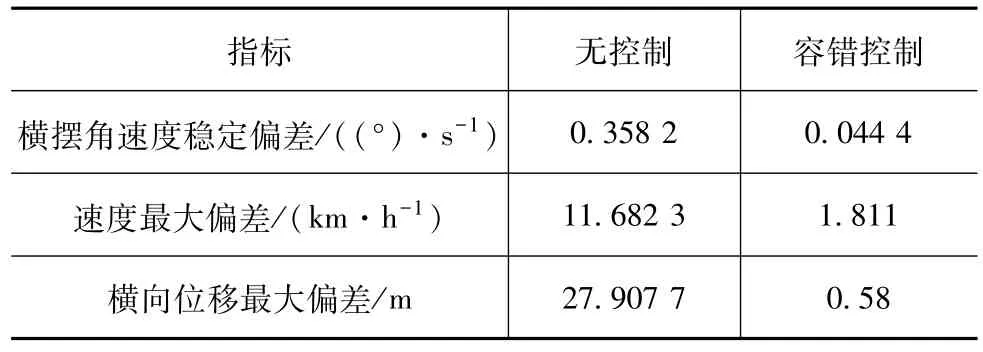
表6 匀速转向工况单轮失效有无控制效果对比

图10 驾驶模拟器实验台架

表7 实验验证工况
由实验结果图11~图16同样可以看出车辆匀速行驶于转弯工况时,左前轮失效,通过如图11所示驱动系统未失效电机和如图12所示转向系统协同控制,保证了车辆纵向能维持如图13所示期望车速行驶。从图15和图16可以看出,横向车辆不会偏离既定轨迹行驶,不失稳以及不跑偏,因此不会导致产生严重交通事故危害驾驶员安全。同样表8统计了驾驶模拟器无控制和有容错控制时车速、横摆角速度、横向位置偏差的实验结果,结果表明驾驶模拟器实验验证结果与仿真结果类似,达到了在驱动系统发生失效以后成功容错控制目的。同时驾驶模拟器验证实验中,系统控制周期小于50 ms,也验证了控制算法具有较好的实时性。

图11 车轮转矩
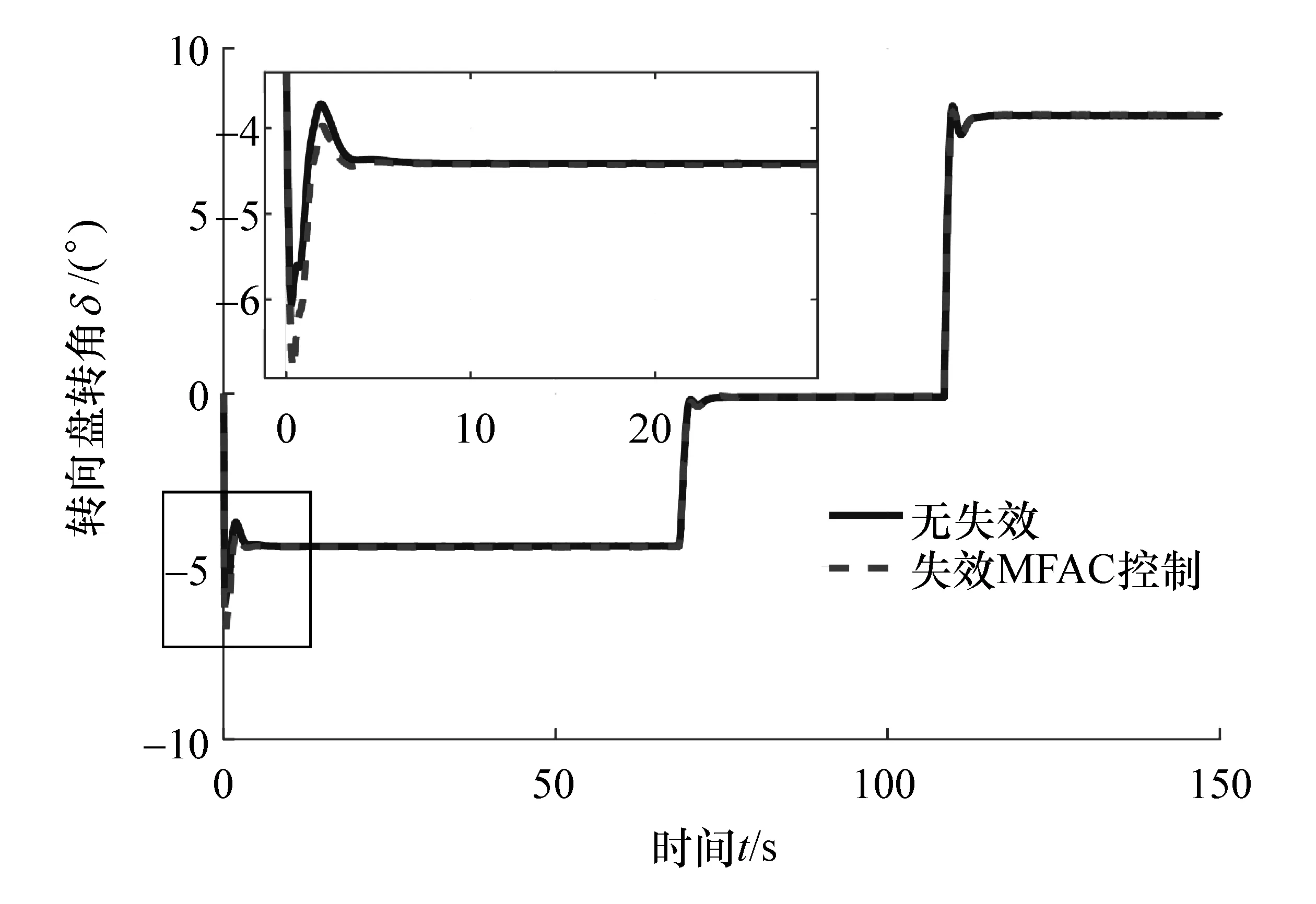
图12 转向盘转角
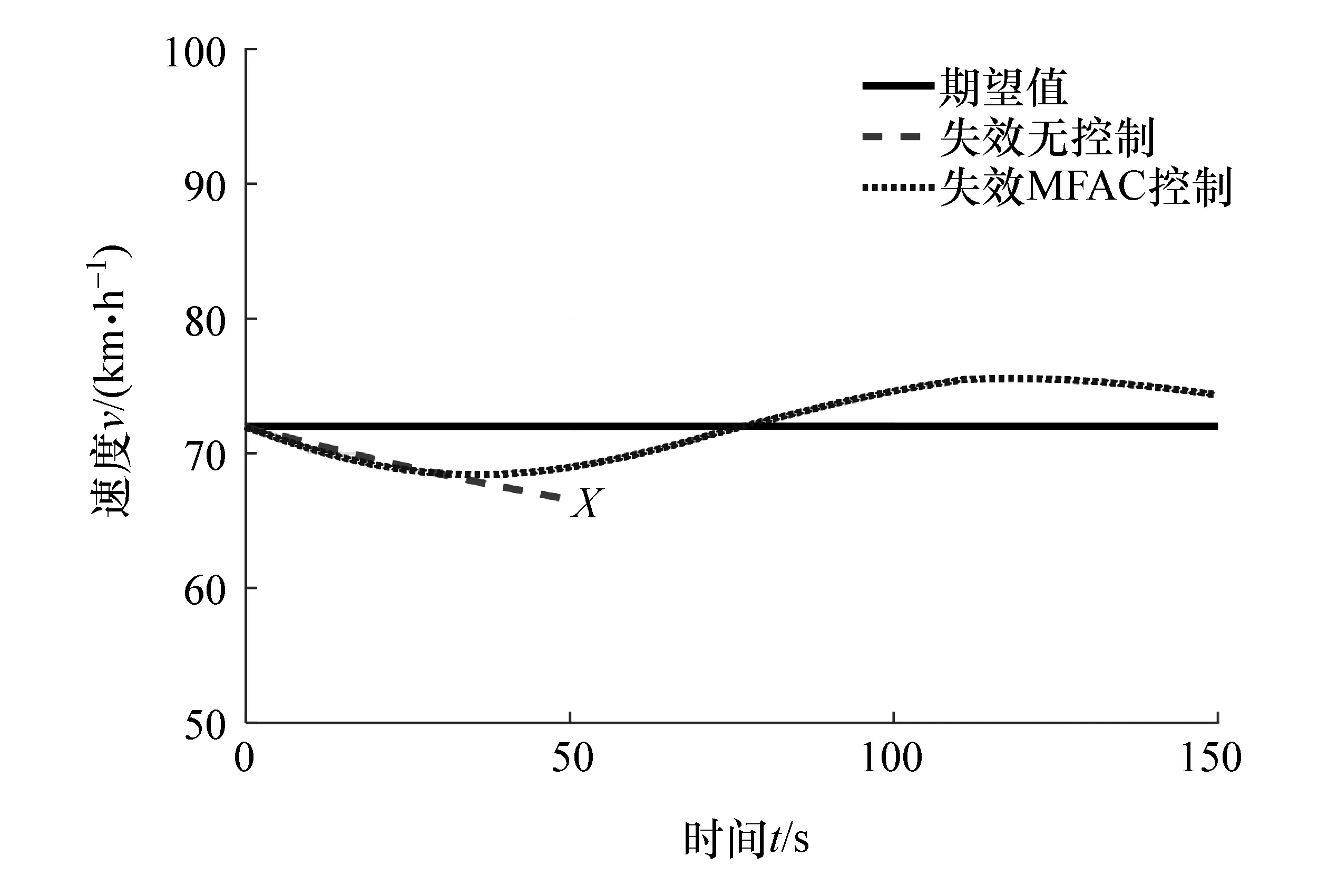
图13 车辆速度
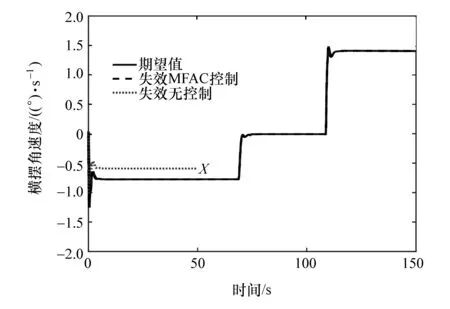
图14 横摆角速度
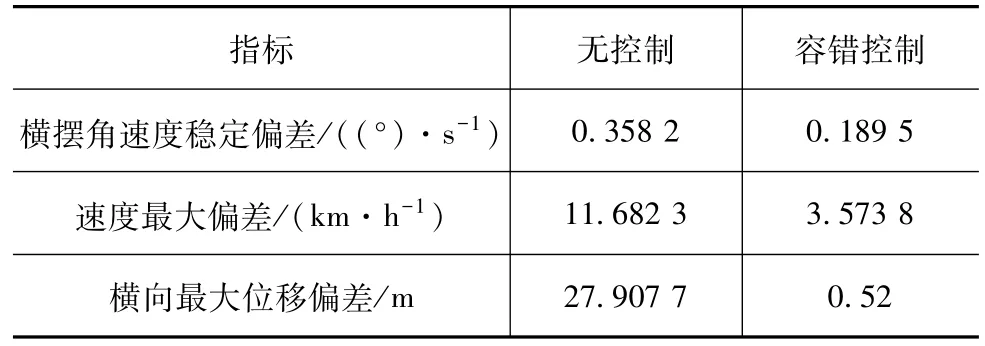
表8 匀速转向工况单轮失效有无控制效果对比
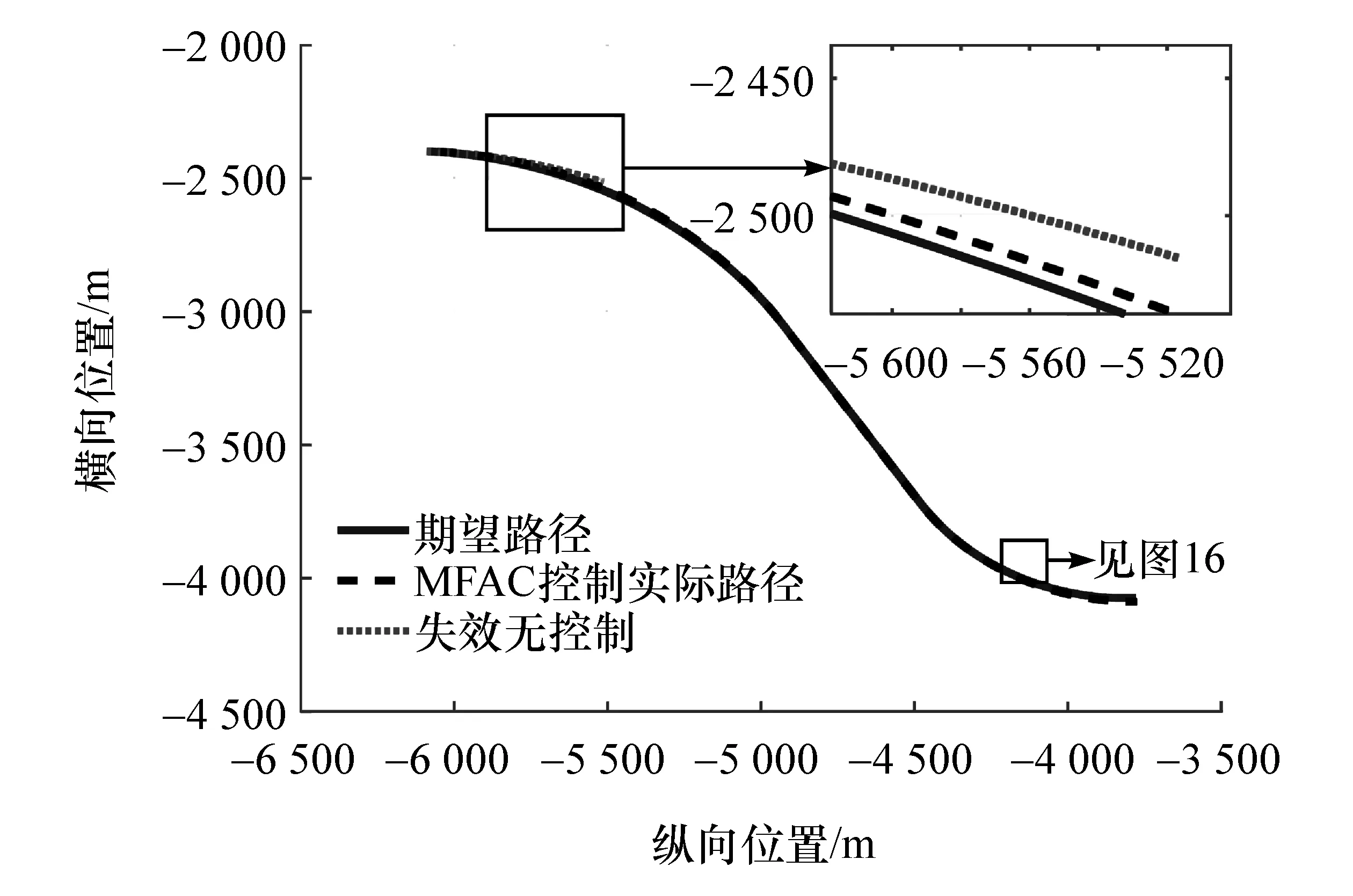
图15 车辆轨迹
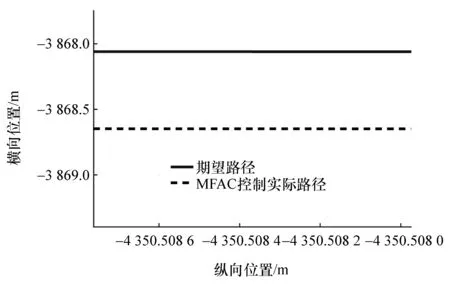
图16 车辆轨迹局部放大图
4 结论
本文中针对分布式电驱动车辆驱动系统失效,利用一种不依赖于系统模型,仅利用系统I/O数据的无模型自适应主动容错控制方法,通过驱动系统与转向系统的协同容错控制,保证分布式电驱动车辆驱动系统失效后既能维持期望车速也不偏离既定轨迹行驶,进而保证了行驶安全,并通过MATLAB/Simulink与CarSim联合仿真和驾驶模拟器实验验证了所提出的方法有效性和实时性。
(1)提出的MIMO-MFAC主动容错控制系统的设计不依赖于系统模型,仅利用系统I/O信息,解决容错系统过分依赖精确故障信息以及由于车辆系统复杂、非线性强、不确定性在建模时带来一系列问题。
(2)在驱动系统各个失效工况下,MIMO-MFAC主动容错控制方法能够实现驱动系统和转向系统的协同容错控制,避免极限工况仅利用驱动系统或者转向系统单一执行器进行容错控制,使执行器极易超出工作负载,无法成功完成容错控制进而引发交通事故。
