旋转车轮气动效应的CFD仿真和风洞实验及减阻优化研究

方 健，王夫亮

（泛亚汽车技术中心有限公司，上海 201206）

前言

当前对传统汽车日益严苛的节能减排和电动汽车延长续航里程的要求，使汽车空气动力学减阻开发越来越受到重视。当车速超过70 km/h时，气动阻力成为行驶阻力的最主要组成部分［1］，汽车气动特性是影响节能减排和续航里程的重要性能，气动减阻优化是整车开发中的重要工作。

关于总气动阻力来源的研究结果显示，上车体引起的风阻约占50%［2-4］，车底、车轮和轮腔区域引起的气动阻力占40%～50%［2-3］，其中由车轮和轮腔引起的气动阻力占 25%～30%［1，5-6］，因此车轮和轮腔是气动减阻开发的重要区域。

然而该区域的流场受到汽车侧面和车底的前方来流以及发动机舱内流场的共同影响，与车身、车底结构和地面之间产生比较强烈的相互干扰［7］，并且旋转车轮还会对这一区域的流场产生能量输入［8-9］，使该处的流场结构更为复杂。目前对该区域的流动现象和流动规律的认识较为有限，减阻开发难度较大。

另一方面，目前车轮及其辐板的设计开发处于整车设计开发过程中较晚的阶段，相应的气动优化工作开展的较少。气动性能CFD计算方案的车轮一般为静止状态，不能准确模拟转动车轮的气动效应。车轮相关的气动减阻优化主要通过风洞实验进行［10］。风洞实验成本较高，周期较长，难以在短时间内对多个设计方案提供快速的气动性能评估和改进建议。另外，风洞实验难以直观呈现车轮与气流的相互作用以及该区域气动阻力的产生机理，影响车轮区域的减阻开发效率。

针对这一问题，本文中采用运动考虑坐标系（moving reference frame，MRF）方法中的多重参考坐标系（multi-reference frame，MRF）方案，对上汽通用两款量产车型进行了车轮静止和旋转状态下的气动特性数值模拟，并与相应的风洞实验结果进行了对比，验证了MRF方法对车轮转动效应模拟结果的准确性，分析了车轮转动条件下车轮-轮腔区域的流场结构特点和气动阻力的形成机理，识别出形成气动阻力的关键区域。

在此基础上对轮辐开口区域进行了多个方案的改型，改型方案计算结果显示轮辐开口径向位置对气动减阻效果的影响规律。本文的研究为气动开发提供了能够快速准确评估车轮造型气动性能的CFD模拟方案，揭示了车轮-轮腔区域的流场分布特性，并为车轮气动减阻优化提供了重要参考。

1 车型和车轮介绍

本文中选用上汽通用的两款量产MPV车型进行研究，分别为MPV-A和MPV-B，如图1所示。两款车型各自的轮胎型号为225/50R17（MPV-A）和225/60R17（MPV-B），如图2所示。

图1 本研究选用的两款车型

图2 两款车型车轮及对应的轮胎

2 风洞实验

本文涉及的风洞实验在上海地面交通工具风洞中心的气动声学风洞进行。风洞喷口面积为27 m2，实验段长度为15 m，实验风速可达到250 km/h，速度偏差＜0.25%，湍流度＜0.3%，实验段流场静压梯度＜0.001/m。

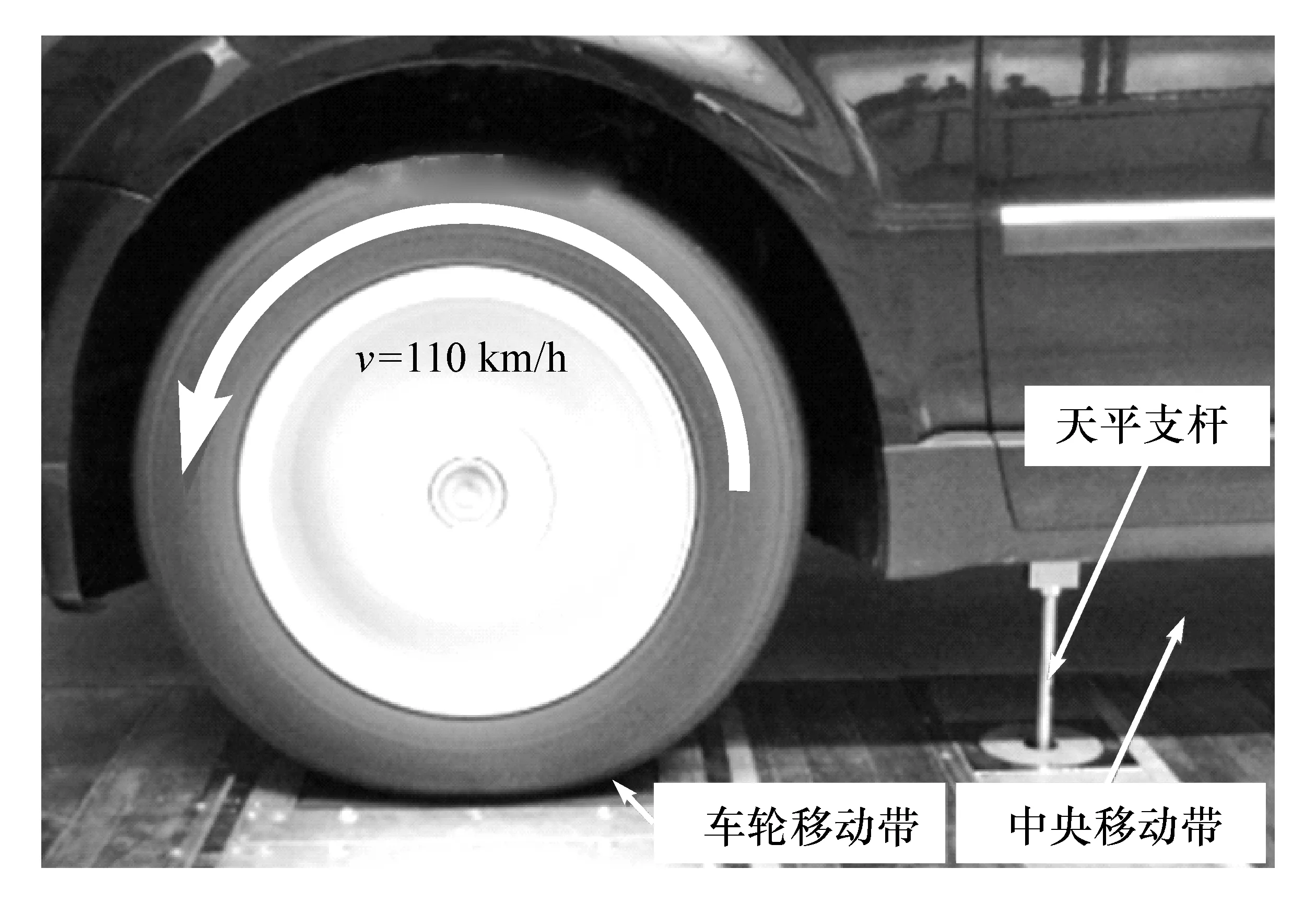
图3 风洞五带系统实现车轮转动和地面移动

风洞配备了先进的五带系统（图3），其中，中央移动带实现地面与汽车之间的相对运动，准确模拟汽车底部的流动状态；而车轮移动带则用来驱动实验车辆的车轮转动，复现汽车在实际路面上行驶时车轮的运动状态，准确模拟转动车轮与流场之间的相互作用。实验过程中车轮移动带和中央移动带都以实验风速v=110 km/h运动，模拟地面效应和实现车轮转动。

3 数值模拟

CFD计算网格保留了后视镜、天线和门把手等较小的几何细节，并准确反映了上车体、发动机舱和底盘的详细外形。车轮部分保留了轮辐的准确外形和车轮接地位置的形状，对轮胎表面的花纹进行了简化。计算网格如图4所示，在车身表面生成棱柱体边界层网格，对车体附近的网格进行了加密，以更准确地捕捉车体附近的复杂流动结构，提高计算准确度。

图4 纵向对称面（y=0）内的部分计算网格

以张量指标形式表示流场控制方程，即时均连续方程、Reynolds方程和标量 φ的时均输运方程［11］：

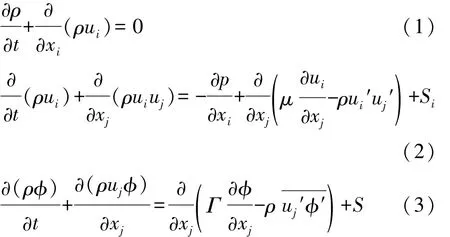
式中 i和 j指标取值范围为（1，2，3）。

冷凝器和散热器内的流场用多孔介质模型进行模拟，多孔介质上的压降-速度关系用Darcy′s定律描述：

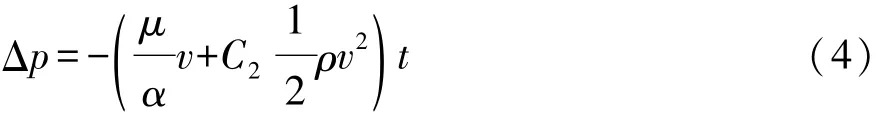
式中：μ为空气的动力黏度；1/α为黏性阻力系数；C2为惯性阻力系数；ρ为空气密度；t为多孔介质厚度。

计算选用Realizable k-ε湍流模型，近壁区流场采用增强型壁面函数进行处理。流场控制方程压力离散格式为Standard，动量、湍流动能和湍流耗散率离散格式为2阶迎风格式，对离散方程的求解选用基于压力修正的SIMPLE算法。

4 运动参考坐标系法模拟车轮转动

运动参考坐标系（MRF）可将惯性坐标系下的非稳态问题转化为运动坐标系下的稳态问题。对于车轮转动，可将流体运动方程转换到运动参考坐标系上，将非稳态车轮转动问题转换成运动参考坐标系的稳态问题，进行稳态求解。

MRF方法的原理如图5所示，运动坐标系相对于惯性（静止）坐标系分别以线速度vt和角速度ω进行平移和旋转运动，a为旋转运动所围绕的轴线的单位方向矢量，因此ω=ωa。

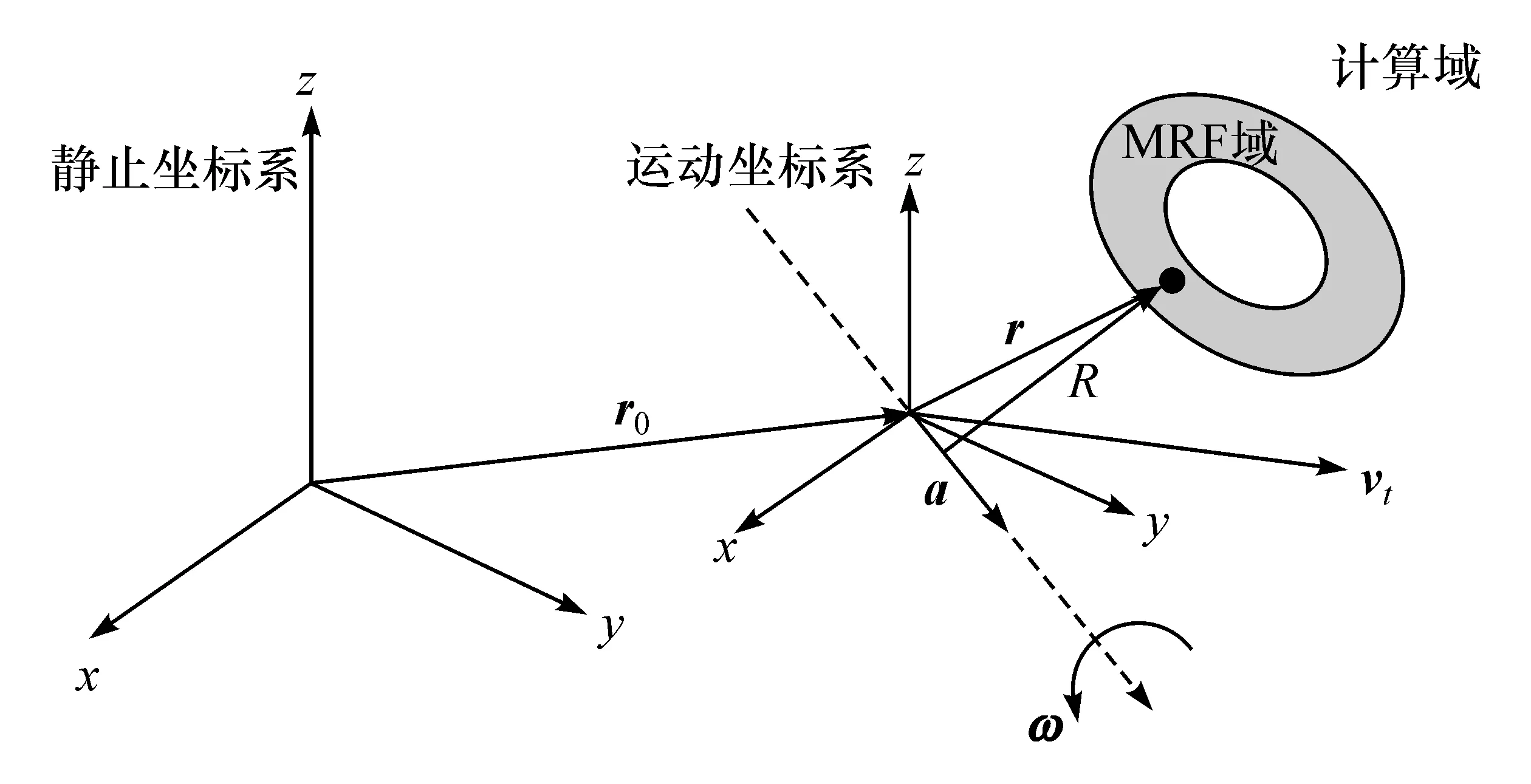
图5 惯性（静止）坐标系和运动坐标系

CFD计算域的任意一点相对于运动参考坐标系原点的位置用位置矢量r来表示，通过如下方程，将流体的速度从静止坐标系转换到运动坐标系：

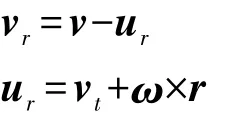
式中：vr为运动坐标系下的相对速度；v为静止坐标系下的绝对速度；ur为运动坐标系相对于惯性坐标系的运动速度。用相对速度vr表示的运动参考坐标系下的流场控制方程［12］如下。

质量守恒方程：

动量守恒方程：

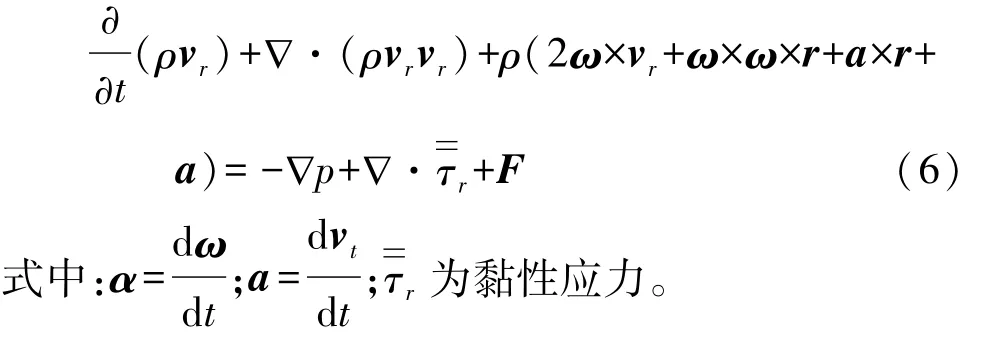
动量守恒方程包含4个附加的加速度项。2ω×vr为科氏加速度，ω×ω×r为向心加速度，这两项适用于运动速度恒定和随时间变化的两种情况。后两项a×r和a分别由转动速度和平移速度随时间变化产生，当平移速度和转动速度恒定时，这两项为零。

如图6所示，在轮辋内外两侧生成两个面（即图中的两个浅色半透明的面），将轮辋包围在其中并与轮辋内圈的表面形成封闭空间，这个封闭的空间即为运动坐标系模拟车轮转动的MRF域。运动坐标系的旋转速度等于车轮的旋转速度ω，轮辋表面设置为相对于运动坐标系静止。

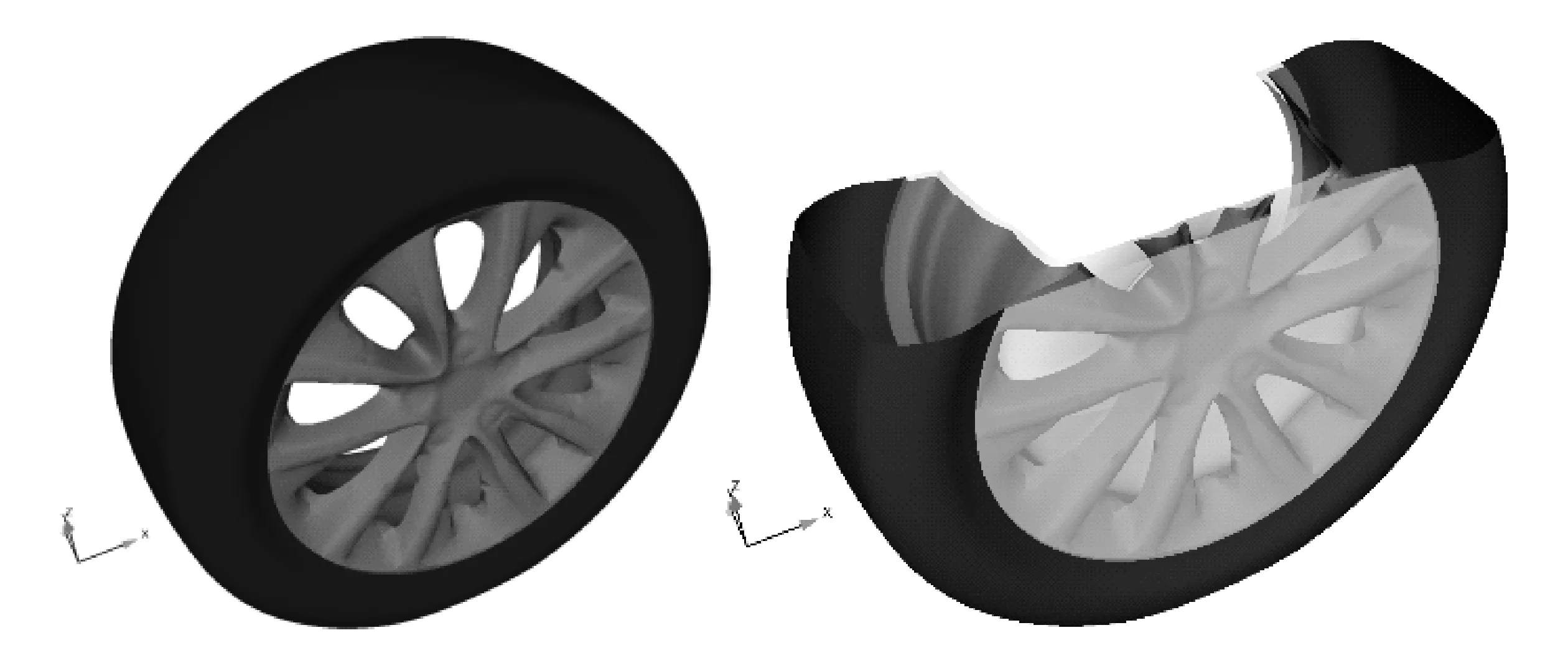
图6 车轮和MRF域的边界设置

图7 示出采用MRF方法来实现车轮转动的情形。此时车轮以角速度ω绕其中心转动，轮胎表面包括其接地点的线速度为110 km/h（地面以同样的速度和方向运动）。

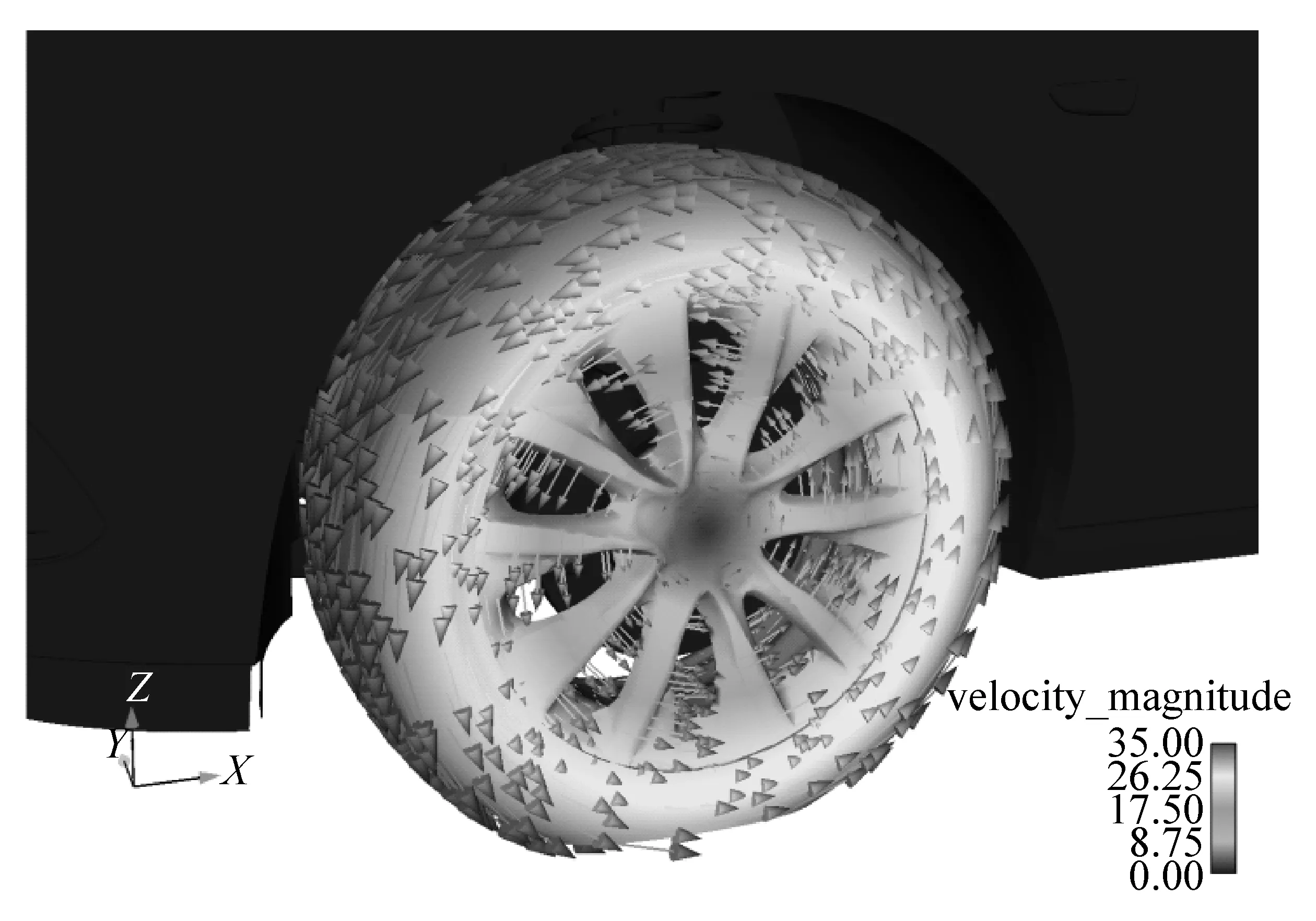
图7 MRF方法实现车轮旋转

5 车轮转动CFD仿真结果的实验验证

将11个研究方案的CFD仿真结果与风洞实验值进行比较，获得仿真值误差结果，如图8所示。从图中可见，相对于车轮静止，11个研究方案在车轮旋转情况下的CFD仿真结果的误差明显减小，仿真值与实验值更为接近，因此可认为车轮旋转CFD仿真方案比车轮静止的方案更为准确，MRF方法模拟车轮旋转是可靠的，能更为准确地模拟车轮旋转的气动效应。

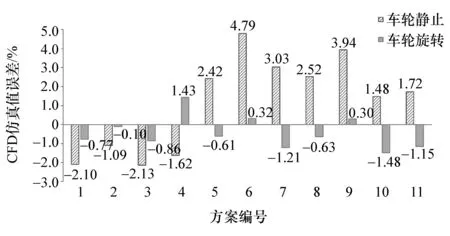
图8 车轮静止和旋转CFD仿真结果误差对比

为进一步验证MRF方法模拟车轮转动效应的准确性，分别对比了MPV-A和MPV-B在车轮静止和车轮转动情况下Cd的CFD计算值和风洞实验值：MPV-A从车轮静止到车轮转动，CFD计算值降低了0.008，风洞实验值降低了 0.007；MPV-B的CFD计算值增加了 0.004，风洞实验值增加了0.003。明显可见，两个车型车轮转动引起Cd变化的方向不同，但两个车型的Cd的CFD计算结果与实验结果的变化趋势一致，且变化量接近，因此可以认为MRF方法较为准确地模拟了车轮转动效应，是一种有效和可靠的模拟方案。

6 转动车轮气动阻力形成机理分析

车轮流动状态（左）和压力分布（右）对比如图9所示。由图左侧的流线图可见，相对于车轮静止，车轮转动引起更多的外侧气流从车轮辐板之间的开口进入轮腔，并与转动的车轮辐板相互作用，在辐板迎风面上形成了更高的压力（如右侧压力分布图所示），导致车轮本身受到的气动阻力增加。

此外，转动车轮情况下，外侧气流主要从辐板径向外端的位置进入轮腔，压力升高的区域也主要集中在这一位置，因此减阻优化应主要考虑这一区域。

图9 车轮流动状态（左）和压力分布（右）对比

7 车轮转动对尾流的影响

车轮静止和车轮转动尾流对比如图10所示。由图可见：MPV-A车轮静止情况下有较多气流内旋并且上卷进入尾流区，尾涡结构贴近尾端表面，容易在表面形成较低的压力；车轮转动时，旋转的车轮为气流注入较多的动能，大部分气流流向后方，尾端表面附近的涡流较少，有助于提高表面压力。

MPV-B在车轮转动情况下后轮后方靠近地面的气流速度增加，流向车身后方，然而仍然有较多气流进入尾流区，在尾端表面形成涡流，与静止车轮的尾流结构很相近，因此对尾端压力分布影响不大。

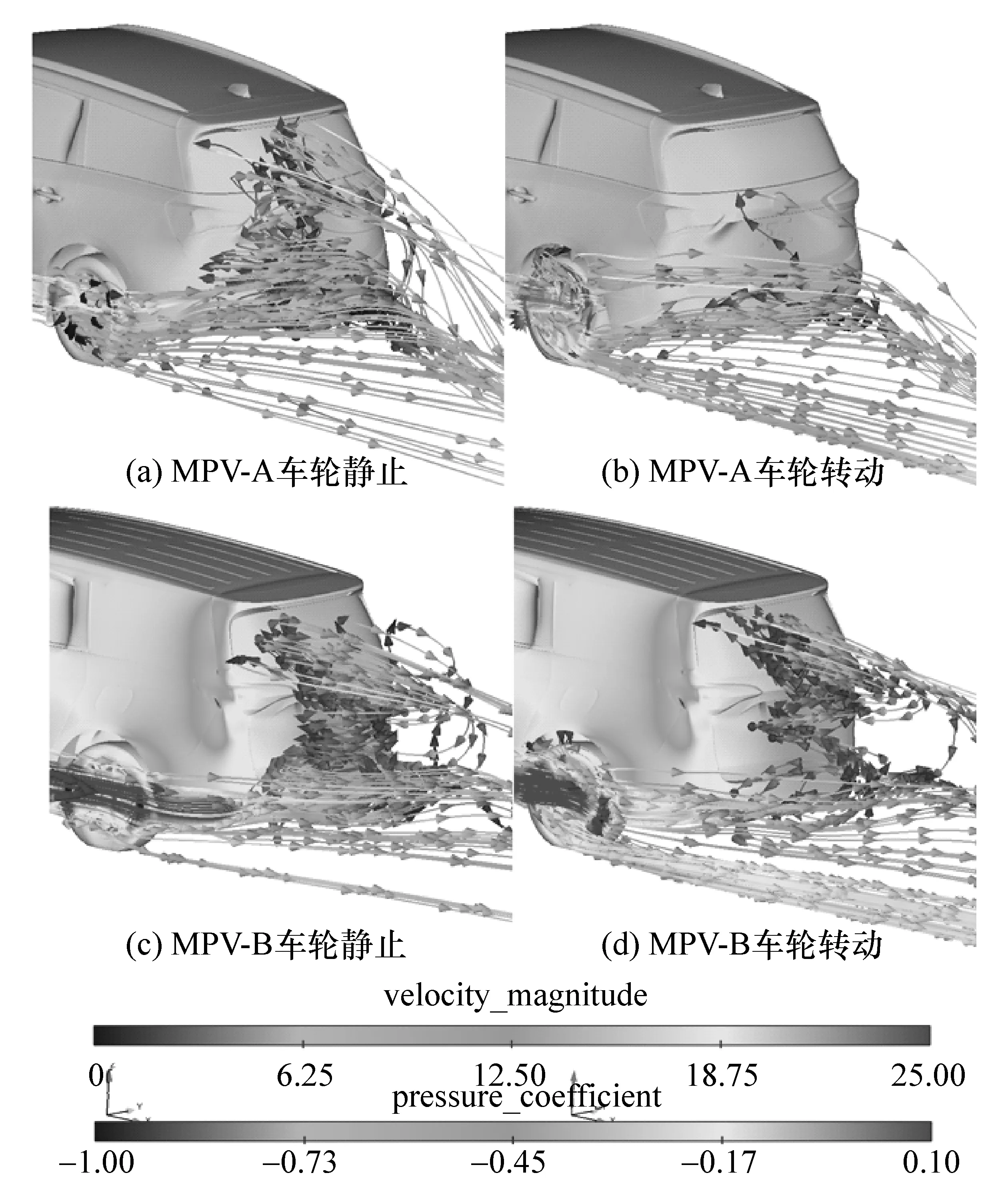
图10 车轮静止和车轮转动尾流对比

图11 为MPV-A和MPV-B分别在车轮静止和车轮旋转情况下的尾部零总压等值面。

图11 尾部零总压等值面对比

由图可见：MPV-A车轮旋转情况下的零总压等值面下方明显前移，向车体靠近，上方稍后移，远离车体，相对于车轮静止，车轮旋转的等值面上下两部分差异减小，更为接近和均衡，均衡的等值面有助于改善尾流结构，减少尾流能量损失，对减阻有利；MPV-B车轮静止和车轮转动情况下尾部零总压等值面变化不大，尾流结构比较相近，车轮转动对尾流结构的改善有限，因此尾部区域的阻力变化不大。

图12为MPV-A和MPV-B分别在车轮静止和车轮旋转情况下的尾端面压力系数对比。可以看出车轮旋转条件下，MPV-A尾端压力明显升高，而MPV-B的尾端面压力分布变化很小，这验证了前文尾部流线和零总压等值面的分析结论。

图12 尾端面压力分布对比

MPV-A车轮旋转一方面引起车轮本身阻力增大，另一方面使车轮与尾部流场相互作用引起尾端面压力升高，造成阻力降低且占优势，导致MPV-A整车风阻下降。MPV-B车轮旋转情况下车轮本身气动阻力增大，尾端面压力升高不明显，综合表现为整车气动阻力升高，这与前文的CFD计算和实验结果一致。

8 车轮气动减阻优化

结合前文图9中车轮转动情况下辐板的压力分布特点，提出车轮辐板开口封闭减阻方案，如图13所示。将车轮辐板开口沿径向由外端向中心方向逐渐用5个同心环形面依次进行封堵，封堵面环宽相等，分别用1，2，3，4，5表示。通过 CFD计算得到 5个封堵方案的Cd结果，与没有封堵的原方案Cd值比较，得到5个封堵环面的各自的减阻贡献量和累计减阻百分比，如图14所示。

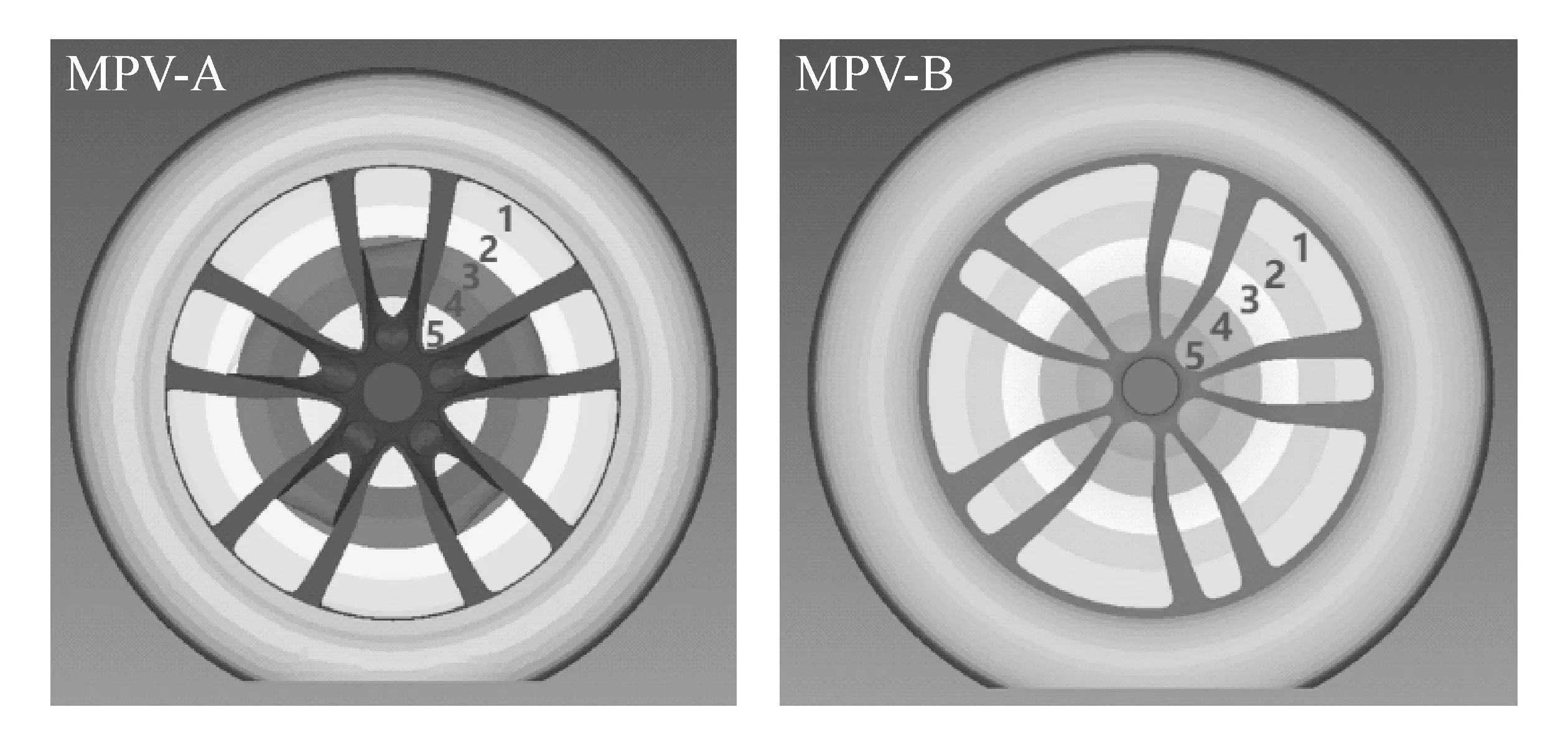
图13 车轮辐板开口封堵减阻方案

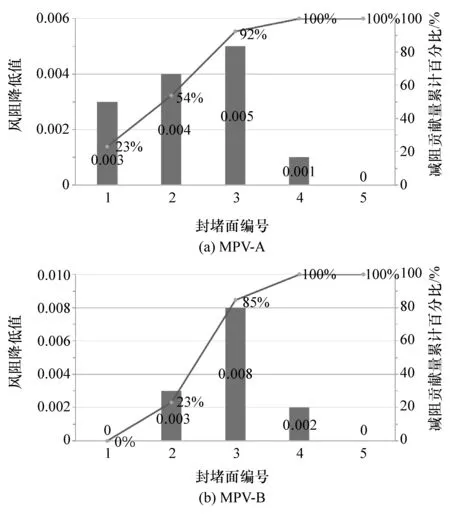
图14 车轮辐板开口封堵方案减阻贡献量

由图可见，第3个封堵环面的减阻贡献量最大，分别达0.005（MPV-A）和0.008（MPV-B），前3个封堵面提供了大部分减阻贡献量，MPV-A的前3个封堵面减阻92%，MPV-B减阻85%。车轮辐板封堵面阻止了车轮外侧气流进入轮腔，抑制了气流与车轮辐板的相互作用，有效降低了车轮的气动阻力。封堵方案可为车轮气动减阻优化提供有益参考。

9 结论

本研究运用 MRF方法，针对上汽通用两款MPV车型MPV-A和MPV-B，实现了对车轮旋转复杂流场的CFD模拟，对比了CFD模拟与实验结果，验证了MRF方法模拟车轮旋转效应的准确性。基于仿真结果分析了车轮在旋转情况下产生气动阻力的机理，以及车轮旋转对尾流结构和尾端压力的影响，阐释了车轮从静止到旋转引起MPV-A的Cd减小，而MPV-B的Cd增加的流场作用机理，提出车轮减阻优化方案并采用CFD计算减阻效果，获得了显著的Cd降低收益。主要结论如下：

（1）MRF可实现对旋转车轮气动效应较为准确的模拟，仿真结果与实验值一致性较好，能为气动开发提供准确的旋转车轮气动特性评估结果；

（2）与车轮静止相比，车轮旋转情况下由于有更多外侧气流进入轮腔区域并与车轮产生强烈的相互作用，引起车轮本身的风阻增加；

（3）车轮旋转运动显著改变了车轮周围和汽车尾部的流场结构，引起气动特性的显著变化，在气动开发过程中，特别是对车轮周围和尾端区域进行气动优化时，须进行车轮旋转的仿真；

（4）封闭车轮辐板开口可显著降低风阻，且辐板径向外端封堵面的减阻贡献较大，靠近轮心的封堵面减阻贡献较小。