基于跟踪误差模型的智能车辆轨迹跟踪方法*

潘世举，李 华，苏致远，徐友春

（陆军军事交通学院，天津 300161）

前言

随着人工智能和机器人技术的不断进步，智能车辆技术迅速发展。其关键技术主要包括精确定位技术、环境感知技术、规划决策和控制技术等［1-3］。轨迹跟踪技术［4-7］主要是控制车辆的横纵向运动，使车辆沿着参考轨迹行驶，其精确程度直接决定了智能车辆的行为表现。

近年来许多学者针对参考轨迹跟踪问题进行了研究。文献［8］中通过车载传感器实时获取行驶轨迹相对于最优路径的偏差信息，采用偏差融合技术的PID控制方法（proportion integration differentiation control），实现铲运车的无人驾驶控制。文献［9］中采用改进的有限时间最优预瞄横向控制算法，其车辆相对于轨迹的横向偏差在±0.3 m内，但预瞄时间的选取较为繁琐。文献［10］中采用基于模糊控制和自校正模型控制方法，实现插秧机以1 m/s行驶时，平均横向偏差为8.7 cm。文献［11］中基于迭代学习控制理论设计迭代学习控制算法，该算法实现了车辆期望路径有限区间内的高精度完全跟踪控制，但仅适用于参考轨迹重复固定的情况。

随着现代控制理论的发展，模型预测控制理论引起了人们的关注。文献［12］中以车辆非线性运动学模型为基础设计控制器，以低于1 m/s的速度跟踪圆形路径时，横向最大误差小于0.1 m。文献［13］中采用车辆动力学模型设计控制器，以15 km/h的速度跟踪轨迹时，可将误差控制在0.2 m范围内。

为进一步提高智能车辆轨迹跟踪精度，本文中采用基于车辆动力学的跟踪误差模型设计模型预测控制器，在Carsim与MATLAB/Simulink构建的联合仿真平台中进行仿真实验，并进行了实车验证，以15 m/s的速度跟踪轨迹时，横向最大误差在0.52 m范围内，跟踪效果较为理想。

1 车辆动力学模型

采用车辆四轮模型分析车辆在运动过程中的受力情况，为简化计算，假设车辆在水平路面上行驶，车辆纵向速度恒定，不考虑横向和纵向空气阻力，前轮转角较小。满足以上条件的车辆动力学模型如图1所示，其中，xoy为车体坐标系，坐标原点o为车辆质心所在点，x轴正方向为车头方向，y轴正方向为垂直车体方向向左，z轴正方向为垂直xoy面向上，XOY为惯性坐标系。

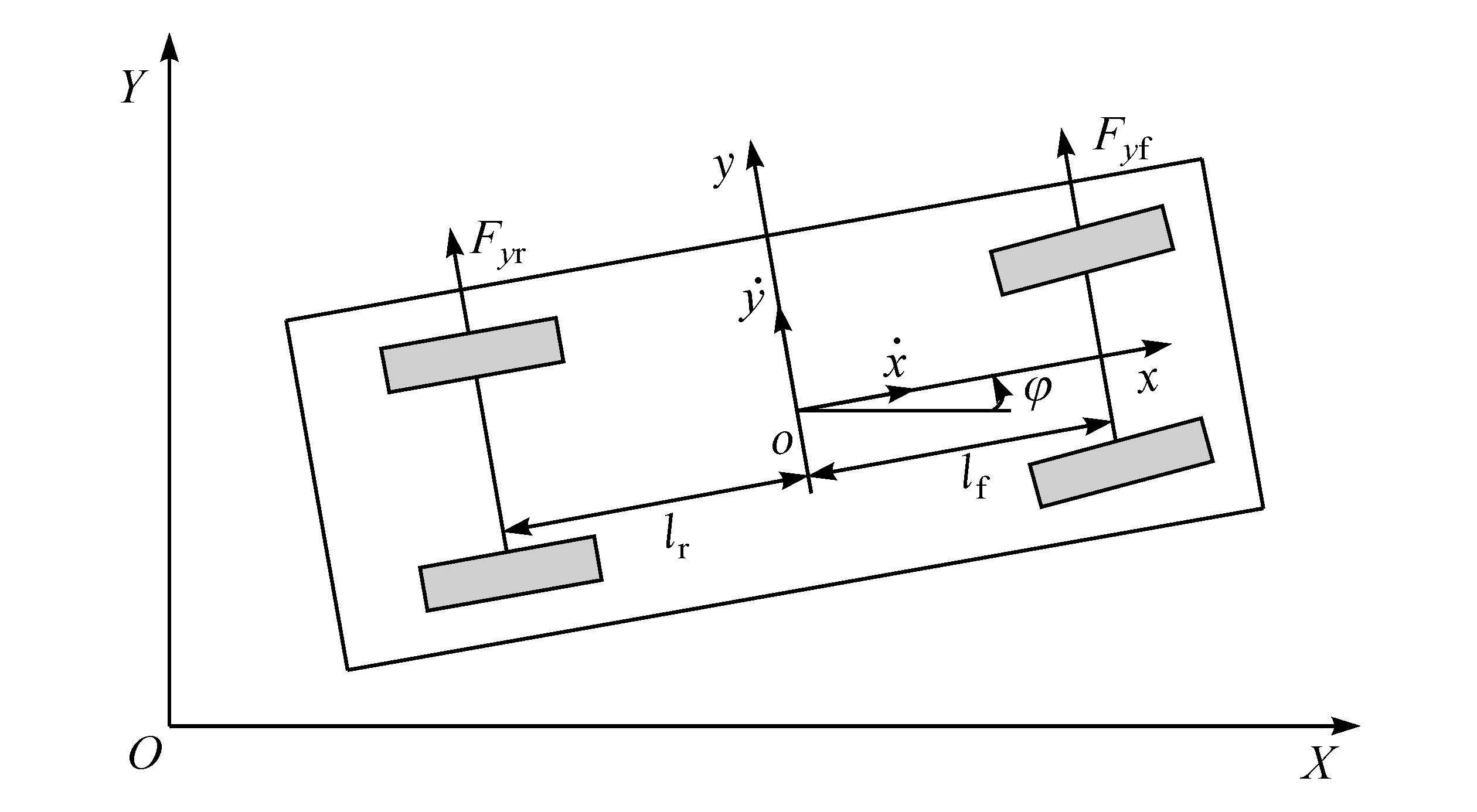
图1 车辆模型

考虑车辆侧向受力和横摆运动，建立如下动力学方程：

式中：m为车辆的质量；φ为车辆在惯性坐标系下的航向；Fyf，Fyr分别为车辆前、后轮受到的侧向力；Iz为车辆绕z轴的转动惯量；lf，lr分别为车辆前、后轴中心到质心的距离。

在小角度假设下，前、后轮受到的侧向力为

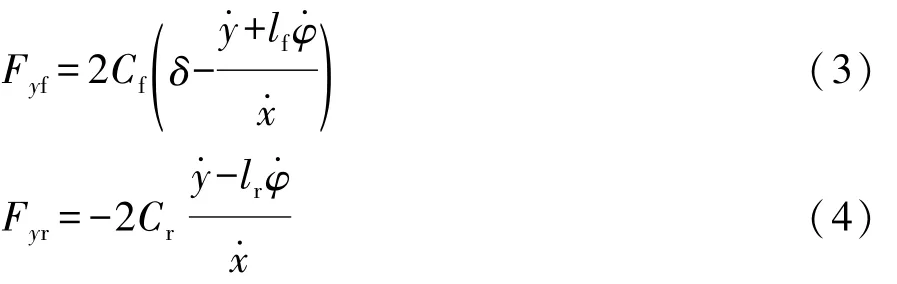
式中：Cf，Cr分别为前、后轮侧偏刚度；δ为前轮转角。联合式（1）～式（4），可得

智能车辆的轨迹跟踪问题是指在惯性坐标系中，设计轨迹跟踪控制器，确定车辆控制输入，使车辆在规定的时刻到达预设的轨迹点，并具备预设的状态，包括位置、航向、速度、加速度等。因此，还应考虑车辆的纵向控制。本文中采用如下车辆纵向运动学方程：

式中：a为车辆的加速度；ar为参考点的加速度；s为车辆相对于轨迹起点的位置；sr为参考点相对于轨迹起点的位置。

定义车辆在参考轨迹跟踪过程中产生的跟踪误差：e1为车辆质心与参考点的横向误差，e2为车辆与参考点的航向误差［14］，e3为车辆与参考点的距离误差，则

综合式（5）～式（10），可得到基于参考轨迹的车辆模型为

可以看出，该系统为非线性系统，为提高模型预测控制计算速度，还需进行线性化和离散化处理。

2 线性时变误差模型

参考轨迹上的任意点均满足式（11），即

其中，由于参考点处于参考轨迹上，则参考状态量 ξr=［0 0 0 0 0 0］T。将式（12）在该点处进行一级泰勒展开，忽略高级项，得

式中：fξ，r为 f相对于 ξ的雅克比矩阵，fu，r为 f相对于u的雅克比矩阵，fw，r为f相对于w的雅克比矩阵。

将式（13）与式（12）相减得

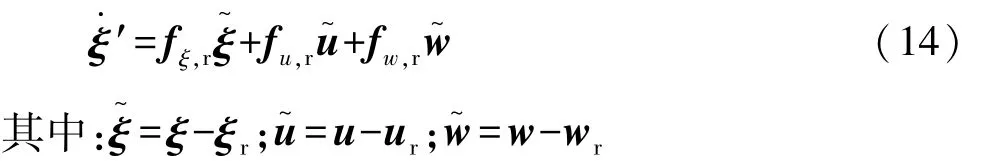
假设预测时域为Np，系统采样时间为k=0，…，Np，系统采样周期为T。车辆的底层控制器会在一个控制周期T内保持控制量的恒定，因此采用零阶保持进行离散的方法能够得到比较精准的符合期望的控制输入量。设计增广向量z=［ξ u w］T，则式（14）可表示为

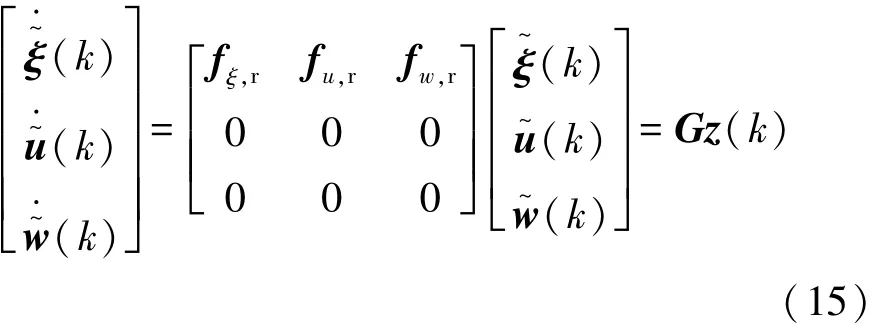
对Gz进行矩阵指数运算，采取零阶保持可得

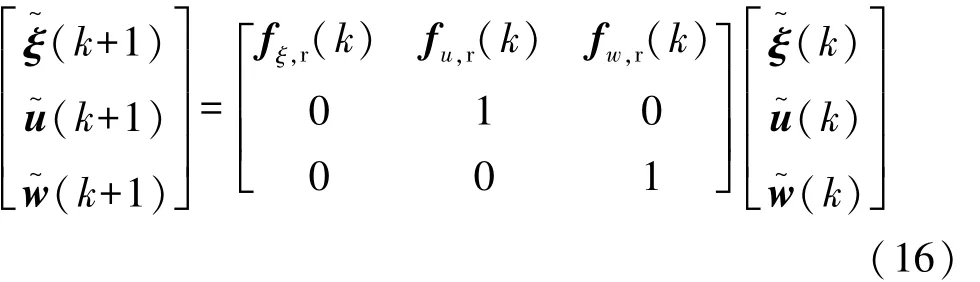
式中第一行即为车辆的线性时变误差模型：

3 轨迹跟踪控制器设计

3.1 预测模型

定义预测时域Np内的车辆的预测输出矩阵、控制量矩阵和附加变量矩阵为

根据式（17），可推导出系统的预测方程为

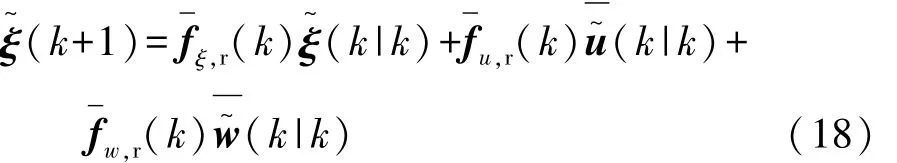
式中：系统状态量预测参数为

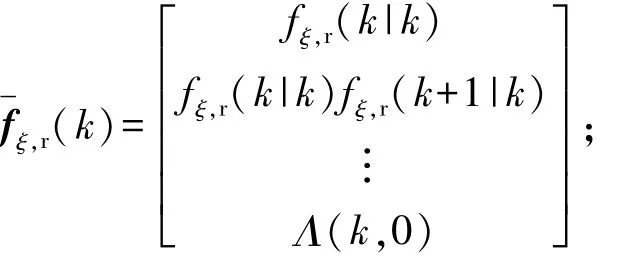
控制量矩阵预测参数为

附加变量预测参数为

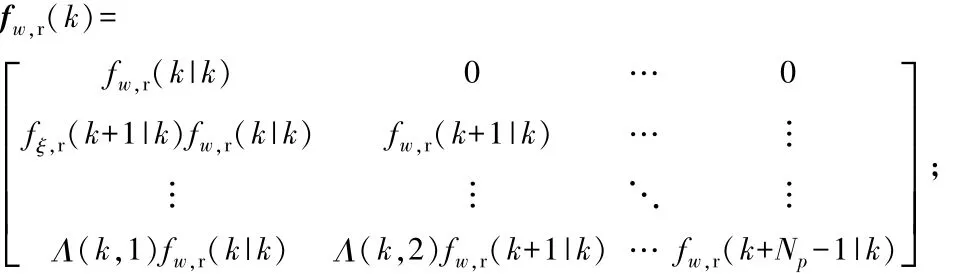
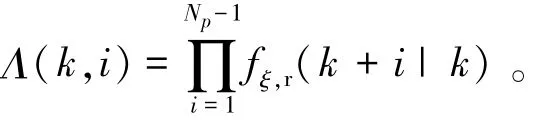
3.2 滚动优化

滚动优化是对系统状态量和控制量的优化，使得车辆能够快速平稳地实现轨迹跟踪，通过目标函数的最优来实现。式（18）中，u～表示的系统控制量未知，可通过设定目标函数进行求解。采用控制增量作为优化目标函数的状态量，同时引入松弛因子，保证系统存在可行解。目标函数表达式为

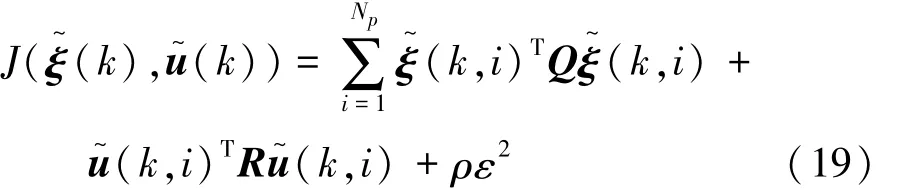
式中：Q为预测时域权重矩阵；R为控制时域权重矩阵；ρ为权值系数；ε为松弛因子。目标函数第1项表示对参考轨迹的快速跟踪能力，第2项表示对控制量变化的优化能力。将式（18）代入式（19），转化为二次规划问题，并考虑系统状态量、控制量和控制增量的约束条件，整理得

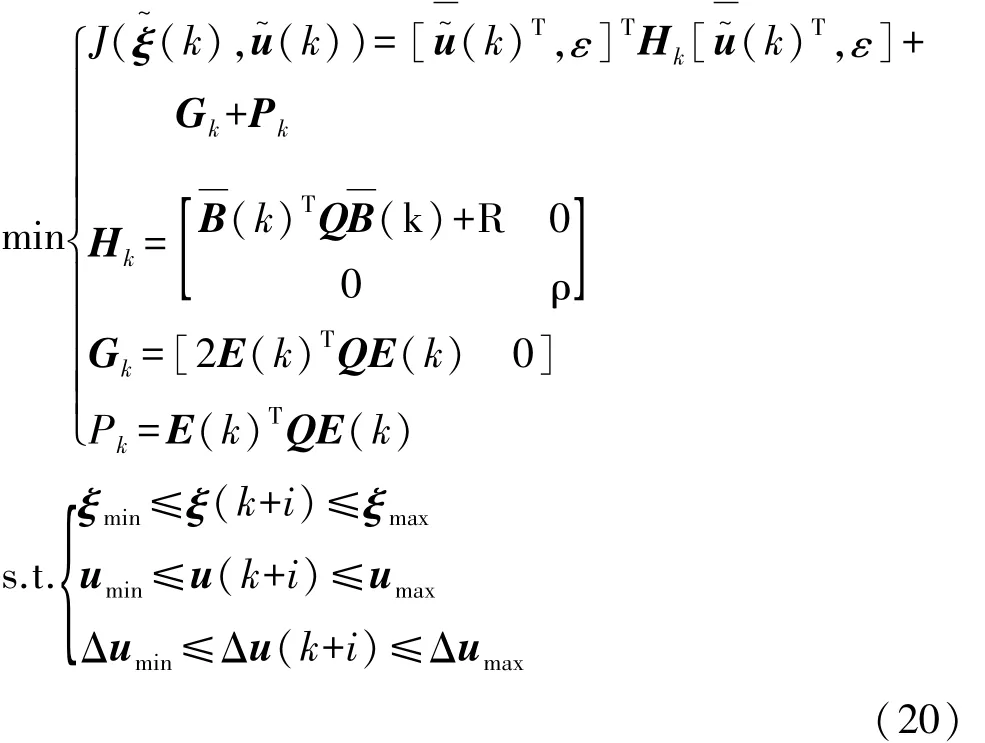
式中：Hk为正定Hessian矩阵；Gk为控制量系数矩阵；Pk为常数；E（k）为预测时域内系统跟踪误差；ξmin和 ξmax为状态量约束最值；umin和 umax为控制量约束最值；Δumin和Δumax为控制增量约束最值。

3.3 反馈校正

在采样时刻k，采用有效集方法进行求解，求取性能指标 J（ξ～（k），u～（k））的最小值，获得最优的控制序列｛u～（k|k），…，u～（k+Np-1|k）｝，取第 1项作为控制增量，计算控制输入量：

在（k+1）时刻，重新计算最优控制序列并将第1项控制增量作用于系统，从而实现最优控制。

4 实验结果与分析

4.1 仿真实验

4.1.1 仿真平台介绍

该仿真平台由CarSim提供车辆动力学模块，通过MATLAB语言编写 S-Function作为控制器，在Simulink中进行整体结构的搭建。

本文中CarSim车辆动力学模型整车质量为1 100 kg，质心与前、后轴中心的距离分别为1 040和1 560 mm，质心高度为540 mm，轮距为1 695 mm，路面附着系数为0.8，滚动阻力系数为0.8。

4.1.2 参考轨迹生成

在轨迹跟踪验证中通常使用双移线进行测试，但标准双移线工况弯道不足以平滑，不易在仿真中应用。本文中借鉴文献［15］中的双移线工况对所建立的控制器进行验证，函数表达为

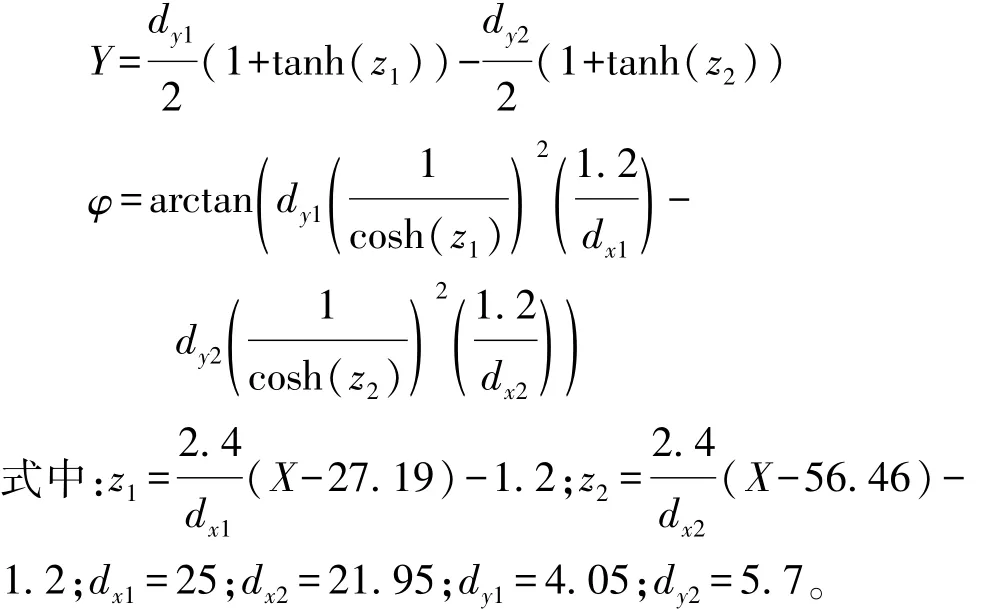
以10 m/s的速度跟踪参考轨迹为例，进行控制器参数调试。随着预测时域的增大，横向跟踪误差减小，主要是因为预测时域较大时，控制器能够更好地预测系统未来输出，根据当前误差及时修正系统输入信号，但同时会增加计算量；控制时域的变化对控制器跟踪效果影响较小，主要是因为反馈校正控制器仅将控制增量的第1个元素作用于系统；随着控制周期变长，横向跟踪误差逐渐减小。仿真控制器参数设置如表1所示。

4.1.3 轨迹跟踪实验

在惯性坐标系下，车辆初始状态为：x=0，y=0，v=0，φ=0，δ=0。采用非线性MPC控制器和本文中设计的线性MPC控制器，以10 m/s的速度进行轨迹跟踪，仿真跟踪结果如图2所示。线性MPC控制器的横向最大误差为0.517 m，航向最大误差为0.053 rad；非线性MPC控制器的横向最大误差为1.496 m，航向最大误差为0.124 rad。保持车辆初始状态不变，采用本文中设计的MPC控制器，分别以5，10和15 m/s的速度进行轨迹跟踪，仿真跟踪结果如图3和图4所示，其中横向最大误差分别为0.452，0.517和0.292 m，航向最大误差分别为0.059，0.053和0.067 rad，侧向最大加速度分别为 0.619，2.585和6.298 m·s-2。

表1 仿真控制器参数

4.2 实车实验

4.2.1 实验平台介绍

图2 线性MPC与普通MPC跟踪效果对比

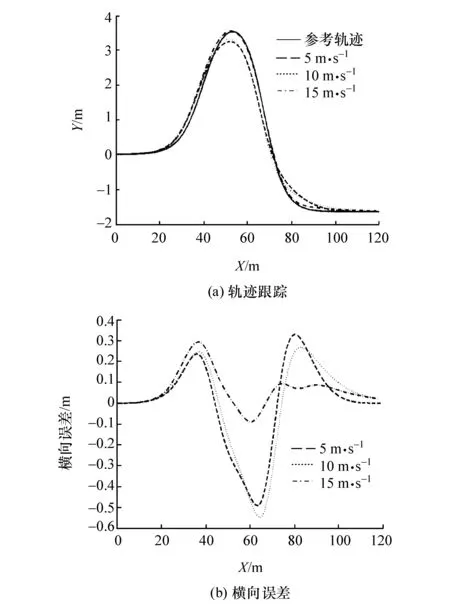
图3 轨迹跟踪与横向误差

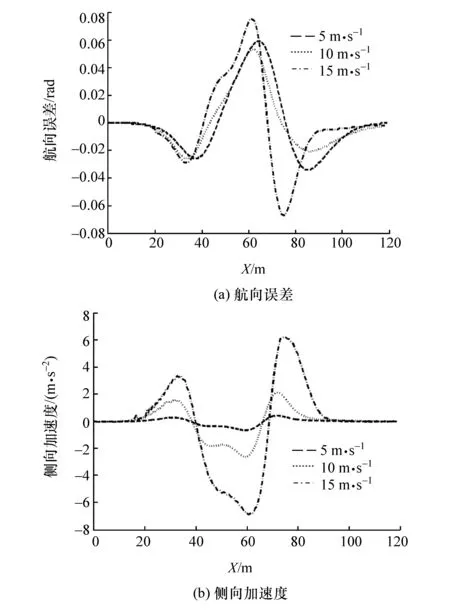
图4 航向误差与侧向加速度

实车实验平台为 JJUV8，该平台改装于长城Wey。硬件架构分为底层、交换层、感知层和计算层。底层主要包含执行机构驱动电路、车辆信号控制电路和中控管理电路；交换层主要包含交换机；感知层包括64线激光雷达、16线激光雷达、组合惯导、摄像头和毫米波雷达；计算层部分包含两台工控机。软件架构包括感知、预测、决策规划和控制4部分，各部分并行计算，利用机器人操作系统的消息发布和订阅机制进行数据交互。

决策规划部分根据感知、预测部分发送的环境信息和车辆自身状态等，实时规划可行驶轨迹，周期为0.1 s；控制部分根据车辆自身状态与参考轨迹的误差计算控制量，周期为0.02 s。初始时，车辆质心位置与参考轨迹起点重合，航向与参考轨迹初始方向一致。实验平台和显示界面如图5所示，其中方框为车辆位置，曲线为参考轨迹。JJUV8实验平台参数如表2所示。

表2 JJUV8实验平台参数

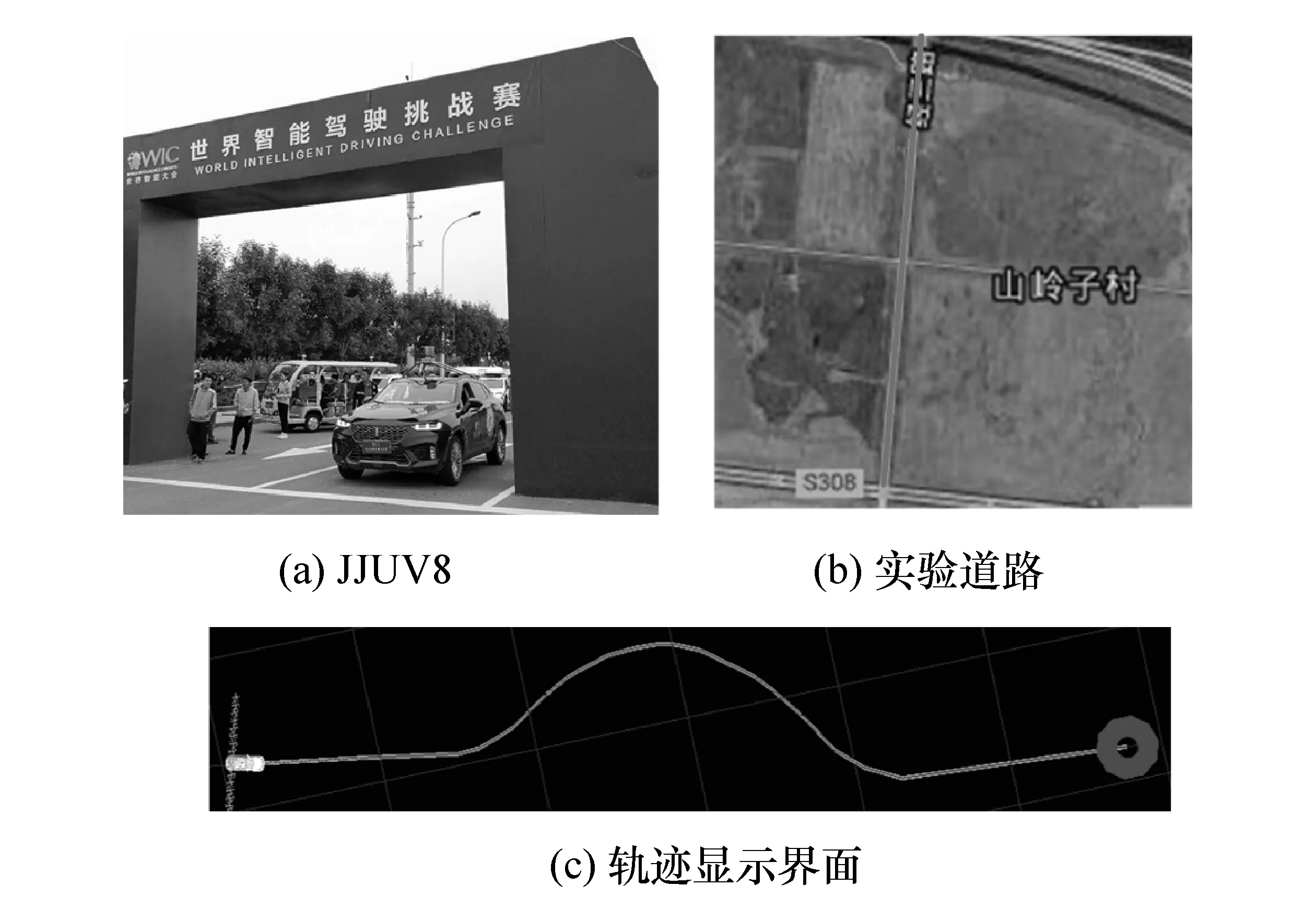
图5 实验平台和轨迹显示界面

4.2.2 轨迹跟踪实验

轨迹跟踪实验中，为保证轨迹跟踪实车实验的可操作性和安全性，在天津空港经济区选取一条道路空旷、车辆和行人较少且路面情况满足要求的道路进行实验，如图5所示。车辆以5和10 m/s的速度分别进行3次实验取其平均值，实车实验跟踪结果如图 6所示，横向最大误差分别为 0.61和0.45 m，航向最大误差分别为0.05和0.06 rad，侧向最大加速度分别为0.54和3.72 m·s-2。

4.3 实验分析

（1）本文中设计的线性 MPC控制器与普通MPC控制器的仿真实验结果相比，横向最大误差减少0.98 m，航向最大误差减少0.071 rad。主要原因是在求解最优解方程的过程中，方程包含了多个最优变量和非线性状态约束，以及由控制量约束和状态量约束组成的线性约束，对于非线性MPC，其求解的复杂程度随系统状态方程阶数的增加而迅速增加，运算时间增加，很难保证实时控制，从而导致跟踪误差增大。

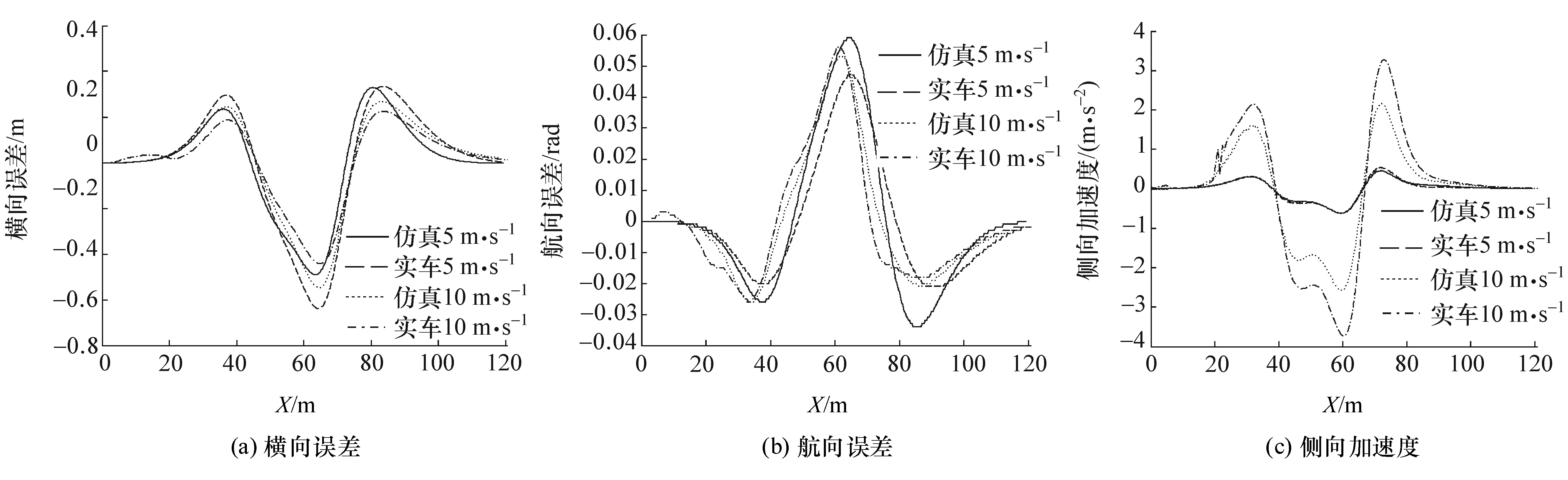
图6 实车轨迹跟踪结果

（2）轨迹跟踪仿真实验结果中，对于5和10 m/s跟踪速度，横向最大误差随速度增大而增大，航向最大误差随速度增大而减小，主要原因是转弯时车辆质心变化导致绕z轴的转动惯量发生变化、前轮转角较大导致小角度假设不成立，控制器预测的车辆运动与实际情况差别增大。15 m/s跟踪速度下横向最大误差较小，航向最大误差较大，主要原因是转弯处的侧向最大加速度大于0.4g，轮胎侧偏特性处于非线性范围、左右车轮载荷变化导致的特性变化等。

（3）轨迹跟踪实车实验结果与仿真实验相比，5 m/s跟踪速度下的横向最大误差增加0.15 m，而航向最大误差减小0.01 rad，主要原因是传感器、执行器和路面不平坦等不确定因素对系统的干扰。10 m/s跟踪速度下的横向最大误差减少0.07 m，航向最大误差增加0.08 rad，主要原因是在仿真环境中路面附着系数和滚动阻力系数均为0.8，而实车实验道路环境相对较差。

5 结论

本文中以车辆动力学模型为基础，提出基于线性时变模型预测控制的轨迹跟踪方法，设计控制器并进行仿真实验与实车实验。仿真实验结果表明，该控制器与普通非线性MPC控制器相比，能够满足实时控制的要求，且跟踪效果更优。在双移线轨迹跟踪过程中，5 m/s时横向最大误差为0.452 m，10 m/s横向最大误差为0.517 m。

利用JJUV8平台进行实车验证，车辆以5 m/s速度跟踪轨迹时，与仿真实验相比，横向最大误差增加0.15 m，航向最大误差减小0.01 rad，基本满足轨迹跟踪的要求。车辆以10 m/s速度跟踪轨迹时，横向最大误差为0.45 m，航向最大误差为0.06 rad。本文中所设计的控制器效果较为理想，能够满足智能车辆的轨迹跟踪要求。

下一步工作将继续研究车辆在纵向速度变化、载荷转移情况下的动力学模型，分析低附着系数和低滚动摩擦因数环境下的控制方法，兼顾车辆运动稳定性，并展开实车实验。