有限域上两类卷积码的构造
2019-09-23李凤伟孙晓明
李凤伟,孙晓明
(枣庄学院 数学与统计学院,山东 枣庄 277160)
0 引言
在编码器复杂度相同的情况下,卷积码的性能优于分组码,因此卷积码几乎被应用在所有无线通信的标准之中.近几年来,卷积码以及量子卷积码受到许多专家学者的注意,相继出现不少优秀的成果.Lee[1]阐述了存储级数等于1的卷积码的重要性,他指出相同比率的卷积码中,存储级数等于1的卷积码比存储级数大于1的卷积码具有更大的自由距离.Hole[2]与Rosenthal[3]利用BCH码分别构造了存储级数等于1的卷积码.通过Reed Solomon码和BCH码,H.Gluesing-Luerssen等研究了双循环卷积码[4].另一方面,对经典卷积码和它们相应属性的研究以及构造最大距离可分 (简称MDS)卷积码也在许多文献中提出.Gluesing-Luerssen等[5]给出了一类强MDS卷积码.最近,Guardia教授[7~10]根据Piret[6]提出的方法构造了MDS卷积码以及量子MDS卷积码并做了进一步的推广;熊茂盛教授[11]研究了存储级数为1的MDS卷积码的构造,同时得到了更多的强MDS卷积码.
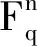
1 相关知识
在这一节里,我们简单地介绍一下负循环码、duadic 码以及卷积码的基本知识和相关的概念.
1.1 负循环码和duadic码
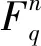
wt(c)=|{j:cj≠0,0≤j≤n-1}|,
常循环码C的最小汉明距离d(C)定义为
d(C):=min{wt(c)|c∈C,c≠0}.
我们把码字c=(c0,c1,…,cn-1)写成多项式形式
c(x)=c0+c1x+…+cn-1xn-1∈Fq[x],
则C是λ-常循环码当且仅当C是环R=Fq[x]/(xn-λ)中的一个理想.由于R的每个理想都是主理想,所以存在首相系数为1的多项式g(x)∈Fq[x],g(x)|(xn-λ),使得
C=(g(x))=g(x)R={a(x)g(x)∈R:a(x)∈R},
这也就是说,λ-常循环码C和g(x)是一一对应的,我们称g(x)为λ-常循环码C的生成多项式,称h(x)=(xn-λ)/g(x)为λ-常循环码C的校验多项式.设β为Fq的某个扩域的一个n次本原单位根,称集合T={1≤i≤n-1:g(βi)=0}为C的定义集,βi称为C的根或零点.显然C由T唯一确定.
对于以g(x)为生成多项式的长度为n,维数为k的q元的常循环码C,g(x),xg(x),…xk-1g(x)构成C的一组Fq基.
设g(x)=g0+g1x+…+gn-kxn-k(gn-k=1),则C的一个生成矩阵可以表示为
设C的校验多项式h(x)=h0+h1x+…+hk-1xk-1,则C的一个校验矩阵可以表示为
Duadic码是循环码中非常重要的一类,是二次剩余码的推广.Duadic码分为两种:even-like Duadic码与odd-like Duadic码.
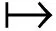
引理1.1.1[12]:(BCH界)设C=(g(x))是长度为n的循环码,gcd(q,n)=1.设β为Fq的某个扩域的一个n次本原单位根,若对某一正整数l,g(x)的根为βl+i,i=1,2,…,d-1,其中d-1≤deg(g(x)),则码C的最小汉明距离至少是d.
引理1.1.2[12]:(singleton界)若存在参数为[n,k,d]的q元码C,其中1≤d≤n-1,则n≥k+d-1.若等号成立,称C为MDS码.
1.2 卷积码
定义 1.2.1比率为k/n参数为(n,k,γ;m,df)q的卷积码V是Fq[D]n的一个子模,它可由多项式矩阵G(D)生成,G(D)=(gij)∈Fq[D]k×n为一个基本不可约的矩阵,即
V={u(D)G(D):u(D)∈Fq[D]k},

在上面的定义中,元素v(D)=(v1(D),v2(D),…,vn(D))∈Fq[D]n的重量定义为
其中wt(vi(D))表示vi(D)的非零系数的个数.若考虑洛朗级数域Fq((D)),定义u(D)的重量为
wt(u(D))=∑i∈Zwt(ui(D)).
如果存在无穷汉明重量的u(D)k∈Fq((D))k,使得u(D)kG(D)的汉明重量有限,我们称生成矩阵G(D)为catastrophic.本文里,我们构造的卷积码都是noncatastrophic.

V⊥={u(D)∈Fq[D]n|
2 新的卷积码的构造


在这一节里,我们将利用代数的方法从循环duadic码和负循环duadic码来构造新的卷积码.首先我们给出一个引理.
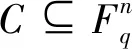
(a) 矩阵G(D)是卷积码V的一个基本不可约的矩阵.

2.1 由循环duadic码构造新的卷积码
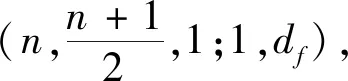
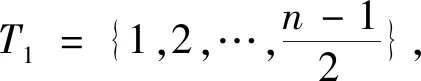
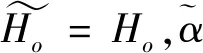
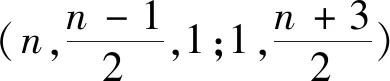

2.2 由负循环duadic码构造新的卷积码
引理 2.2.1[15]令s∈{1,2,…,2n-1}且(s,2n)=1.设q≡3(mod4)且n为oddlyeven,则存在多项式A(x),B(x)和置换
使得
xn+1=A(x)B(x)(x2+1),
这里μs(A(x))=(B(x)),μs(B(x))=(A(x)).令
C1=<(x2+1)A(x)>,C2=<(x2+1)B(x)>,D1=
则C1,C2是一对even-like负循环duadic码,D1,D2一对odd-like负循环duadic码.
定理 2.2.2 设p,q为不同的奇素数且q≡3(mod4).令n=2pt,(n,q)=1.设r为q模n的乘法阶,如果2 证明:由[15,定理8]可知: x2pt+1=λA(x)A*(x)(x2+1), 其中λ∈Fq,A(x)∈Fq[x],A*(x)为A(x)的互反多项式.令 C1=<(x2+1)A(x)>,C2=<(x2+1)A*(x)>, D1=