扩展卷积码生成矩阵的统一表述*

包 昕,游 凌

(盲信号处理重点实验室，成都　610041)

扩展卷积码生成矩阵的统一表述*

包 昕**,游 凌

(盲信号处理重点实验室，成都610041)

针对在删除卷积码识别过程中缺乏对扩展卷积码先验认知的问题,提出了一种求解母码与扩展卷积码生成矩阵的统一表述方法。通过分析编码器输入输出关系的基本物理意义,先后以(n, 1,m)、(n,k,m)作为母码,构建了其与扩展后编码器多项式系数的对应关系模型,归纳和证明了扩展卷积码生成矩阵的统一表述定理。验证结果表明:该定理能够对扩展卷积码生成矩阵实现快速计算,为遍历和重建删除卷积码的删除图样和母码生成矩阵提供方便。

盲识别;删除卷积码;母码;扩展卷积码;生成矩阵

引用格式:包昕，游凌.扩展卷积码生成矩阵的统一表述[J].电讯技术，2016，56(3)：267-272.[BAO Xin，YOU Ling.A unified descriPtion of generator matrix of exPansion convo1utiona1 codes[J].Te1ecommunication Engineering，2016，56(3)：267-272.]

1　引 言

E1ias于1955年最早提出卷积码，Cain于1979年给出了删除卷积码的构想。半个世纪以来，随着其编码、译码技术的深入研究，卷积码已被广泛应用于卫星、深空等多种通信系统中，成为CCSDS、IESS、DVB-S等协议/标准中的信道编码解决方案。

与此同时，人们针对卷积码识别问题也抱有浓厚的兴趣。Rice[1]证明(n，1，m)卷积码的识别可等价于LRS问题中关键方程(Key Equation，KE)的求解；Fi1io1[2]将BM算法引入前述问题中；邹艳[3]则进一步推广KE，给出了基于Gröbner基快速合冲的识别算法。利用卷积码的代数结构，刘建成[4]和杨晓静[5]分别研究了矩阵分析方法；Wang[6]和Xie[7]建立了基于欧几里德算法的识别模型；Marazin[8]使用迭代策略，给出了基于对偶码组的识别思想。在误码条件下，Dinge1[9]和Barbier[10]提出了能够规避误码码组的随机高斯消元法；张立民[11]引入Wa1sh -Hadamard变换，可在变元数不大的条件下实现卷积码校验向量的有限穷举。

删除卷积码的识别问题更为复杂。文献[12-14]将其分为三步：第1步，获得码流的等效校验矩阵HP；第2步，求解HP在某准则下的正交矩阵，即等效生成矩阵GP；第3步，由GP重建扩展生成矩阵G[M]、母码生成矩阵G和删除图样P。对于第1步，即等效校验矩阵HP的估计问题，可依赖前述一般卷积码识别方法。因此，第2步和第3步才是删除卷积码识别问题的核心和难点。陆佩忠[12]研究了(2，1，) m卷积码作为母码的盲识别问题，通过搜索可能的删除图样，建立并求解了HP和GP的方程组。C1uzeau[13]重点讨论了如何获得一个适合译码的最佳等效生成矩阵G。Marazin[14]系统研究了母码为(n，k，) m卷积码时的删除卷积码的代数求解方法。

显然，正确描述扩展卷积码生成矩阵G[M]的基本构造形态及其与母码G的对应关系，有助于上述识别问题第3步的快速解决。本文尝试从简单的物理意义出发，建立两者的对应关系模型，推导其数学表示形式，以作为删除卷积码识别问题的补充。

2　问题描述及符号定义

删除卷积码是一种由己知卷积码构造而来的高码率卷积码，具有构造简单、码率灵活和译码器可以通用等优点。

给定(n，k，) m卷积码的多项式生成矩阵

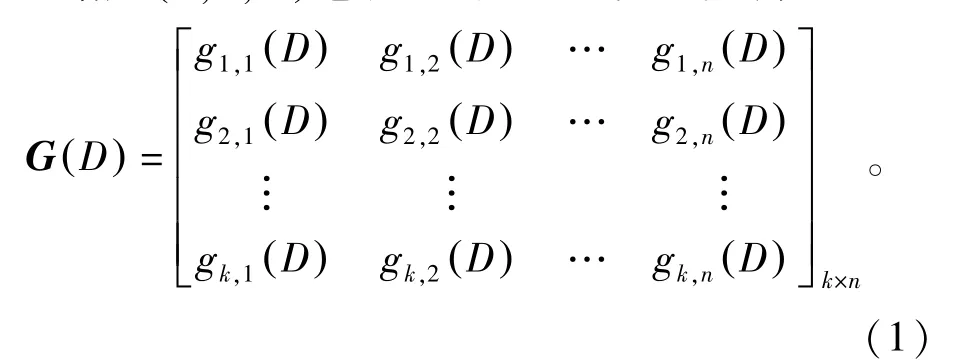
式中：gi，j(D)=gi，j0D0+gi，j1D1+…+gi，jmDm为生成多项式，i=1，2，…，k，j=1，2，…，n，D表示延迟运算。因此，编码过程可记为

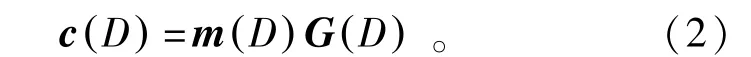
式中：m(D)为信息序列；c(D)为编码序列。如果给定扩展因子M＞1，使得在一个节拍内向编码器输入信息比特数由原来的k个扩展为Mk个，则输出编码比特数将由原来的n个扩展为Mn个。此时，(n，k，m)卷积码将等效于(Mn，Mk，m')扩展卷积码，其生成多项式矩阵可表示为

删除卷积码即是在C[M]基础上，结合事先给定的删除图样P，对输出序列中特定比特予以删除而得到的。P是一个规模为n×M的二元矩阵，其中1的个数为N，对应予以保留的比特位置。最终，可以得到码率为kp/np=N/kM的(np，kp，mp)删除卷积码CP。图1给出了以上构造流程及符号定义。

图1　删除卷积码构造流程Fig.1 The generating form of Punctured convo1utiona1 code

扩展卷积码等效生成矩阵的表述问题是指：已知母码C的生成矩阵G(D)k×n，在给定扩展因子M＞1后，如何获得扩展卷积码C[M]的扩展生成矩阵G[M](D)Mk×Mn。Shen[15]最早研究了该问题，给出了一种复杂的表述形式；陈发新[16]以示例的形式，演算了当C为(n，1，m)时的计算过程。本文将从基本物理意义出发，系统建立(n，1，m)↔(Mn，M，m)、(n，k，m)↔(Mn，Mk，m)生成矩阵的统一表述模型。

3　(n,1,m)的扩展卷积码生成矩阵

设母码C记作(n，1，m)，其扩展卷积码C[M]记作(Mn，M，m)。

(1)当输入序列为足够长序列[100…0]时，由编码公式(2)可知，序列c(D)可表示为

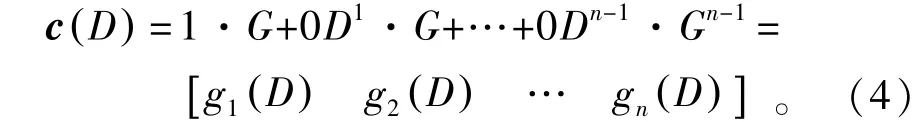
用图2表示时可见，编码器的n个支路分别依次输出G(D)中n个支路抽头多项式的系数。

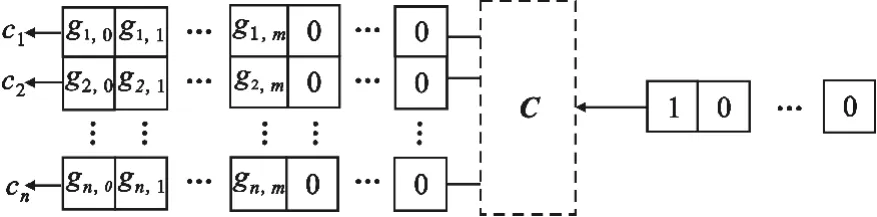
图2　(n，1，m)卷积码的第1类输出情况Fig.2 The 1st outPut situation of(n，1，m)convo1utiona1 code

同样，将输入序列串并转换，则c[M]可表示为

用图3表示可见，编码器的Mn个支路分别依次输出G[M](D)第一行Mn个支路抽头多项式的系数。

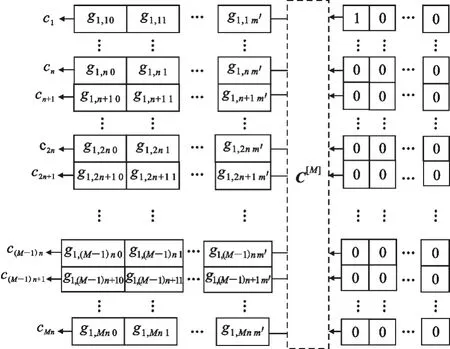
图3　(Mn，M，m')卷积码的第1类输出情况Fig.3 The 1st outPut situation of(Mn，M，m')convo1utiona1 code

比较图2和图3，可以直观地确认G(D)各支路与G[M](D)第一行各支路的系数对应关系。首先观察图3支路c1，可得如下关系式：

式中：g1，0，g1，M，…，g1，M分别表示G(D)中子生成多项式g1(D)内第0，M，…，nM个系数；g1，10，g1，11，…，g1，1n分别表示G[M](D)中子生成多项式g(D)内第0，1，…，n个系数。显然，g1，10=g1，0，g1，11=g1，M，…，g1，1n=g1，nM，即g(D)的系数相当于从中g1(D)第0个系数处开始的M次采样。

以此类推，有

的系数相当于分别从G (D )中g1(D )的第0，1，…，M-1个系数处开始的M次采样。

继续讨论图3支路c2，可得如下多项式：

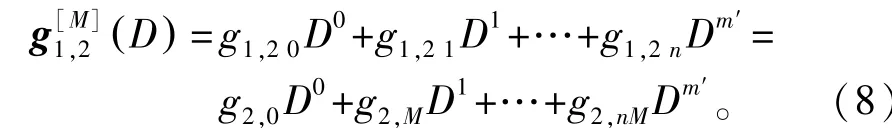
即G[M](D)中g(D)系数相当于从G(D)中g2(D)第0个系数处开始的M次采样。以此类推，我们可最终归纳出G[M](D)中g(D)，j∈[1，nM]的统一表述：

(2)当输入序列为足够长序列[010…0]时，对于C，输出序列

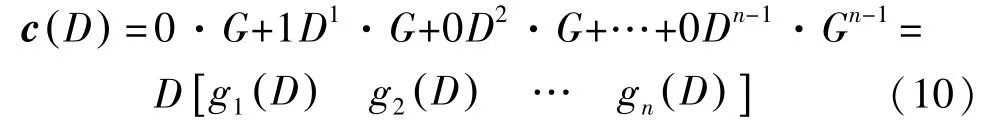
可用图4表示。可见，编码器的n个支路分别依次输出G(D)中n个支路抽头多项式的系数，不过与图2相比存在一个节拍的延迟。

图4　(n，1，m)卷积码的第2类输出情况Fig.4 The 2nd outPut situation of(n，1，m)convo1utiona1 code

而对于C[M]，输出序列

可用图5表示。可见，编码器的Mn个支路分别依次输出G[M](D)第二行Mn个支路抽头多项式的系数。

图5　(Mn，M，m')卷积码的第2类输出情况Fig.5 The 2nd outPut situation of(Mn，M，m')convo1utiona1 code

使用与前述类似的归纳总结方法，我们直接给出G[M](D)中g(D)(j∈[1，nM])的统一表述：

(3)换用其他诸如[0010…0]、[00010…0]形式的输入序列，我们可最终获得如下定理。

定理1 (n，1，m)卷积码及其扩展卷积码(Mn，M，m')的生成多项式具有如下变换方式：

式中：α=(j-1) mod n+1；β=⎿[j-(i-1) n -1]/n」；m'=「(m+2)/M⏋-1。即G[M](D)中g[i，Mj](D)系数相当于从G(D)中gα(D)的第β个系数处开始的M次采样，且当β+ln＜0或β+ln＞m时，gα，β+ln=0。

该定理可看作Shen[15]和陈发新[16]结论的另一种等效表述，并更具实用意义。

4　(n,k,m)的扩展卷积码生成矩阵

运用同样的分析方法，本节讨论(n，k，m)卷积码C的生成矩阵G(D)与(Mn，Mk，m)卷积码C[M]的生成矩阵G[M](D)两者间的统一表述问题。

(1)设一次性输入足够长序列[10…0]，对于C，输出序列

用图6表示时可见，编码器的n个支路分别依次输出G(D)第一行各个抽头多项式的系数。

图6　(n，k，m)卷积码的第1类输出情况Fig.6 The 1st outPut situation of(n，k，m)convo1utiona1 code

用图7表示时可见，编码器的Mn个支路分别依次输出G[M](D)第一行各个抽头多项式的系数，

图7　(Mn，Mk，m)卷积码的第1类输出情况Fig.7 The 1st outPut situation of(Mn，Mk，m)convo1utiona1 code

比较图6和图7的输出序列，可获得G[M](D)中g(D)(j∈[1，nM])的统一表述：

(2)当输入序列为足够长序列[010…0]，对于C，输出序列

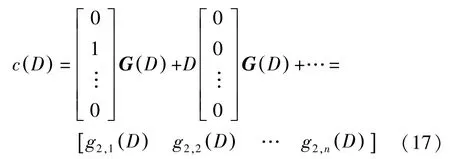
用图8表示时可见，编码器的n个支路分别依次输出G(D)第二行各个抽头多项式的系数。

图8　(n，k，m)卷积码的第2类输出情况Fig.8 The 2nd outPut situation of(n，k，m)convo1utiona1 code

用图9表示时可见，编码器的Mn个支路分别依次输出G[M](D)第二行各个抽头多项式的系数。

图9　(Mn，Mk，m)卷积码的第2类输出情况Fig.9 The 2nd outPut situation of(Mn，Mk，m)convo1utiona1 code

通过换用其他输入序列，可最终获得如下定理。

定理2 (n，k，m)卷积码及其扩展卷积码(Mn，Mk，m')生成多项式具有如下变换方式：

式中：α=(i-1) mod k+1；β=(j-1) modn+1；γ=[j-(i-1)/k」n -1]/n」；m'=(m+2)/M-1。即G[M](D)中g(D)系数相当于从G(D)中gα，β(D)的第γ个系数处开始的M次采样，且当γ+ln＜0或γ +ln＞m时，gα，βγ+ln=0。

显然，定理2是定理1的加强。

5　验证

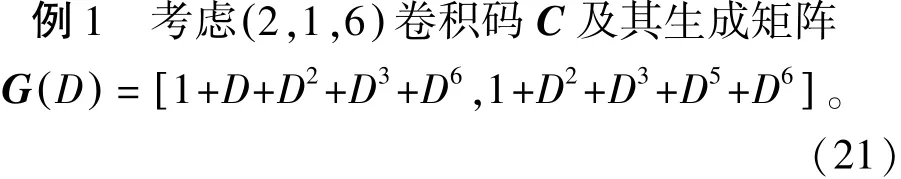
式中：n=2；k=1；m=6。设扩展因子M=3，分别使用定理1和定理2，均可得C[]3的生成矩阵

与熟知的(4，3，) 2删除卷积码生成矩阵完全相同。

例2 考虑(3，2，) 3卷积码C及其生成矩阵

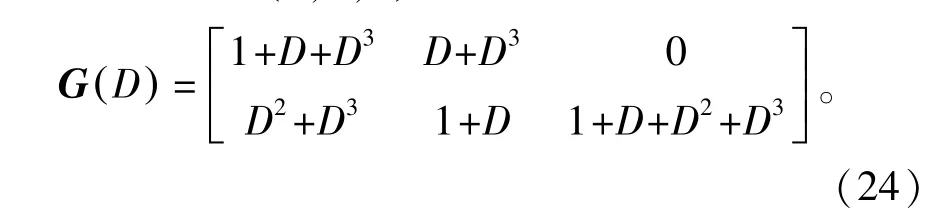
式中：n=3；k=2；m=3。设定扩展因子M=2，使用定理2，可得C[]2生成矩阵

6　结束语

本文研究了删除卷积码识别问题中的重要子课题，即卷积码母码与扩展卷积码生成矩阵的统一表述问题。从编码器输入输出的基本物理意义出发，先后分析和建立了(n，1，m)↔(Mn，M，m)和(n，k，m)↔(Mn，Mk，m)的编码序列输出模型，归纳和证明了其生成矩阵的统一表述定理，并进行了相应验证计算。本文所给出的计算方法可用于加速删除卷积码识别删除图样的遍历过程，也可应用于母码生成矩阵的快速恢复。

[1] RICE B.Determining the Parameter of a rate 1/n convo-1utiona1 encoder over GF(q)[C]//Proceedings of the 3rd Internationa1 Conference on Finite Fie1ds and APP1ications.G1asgow，USA：IEEE，1995：1-5.

[2] FILIOL E.Reconstruction of convo1utiona1 encoders over GF(q)[J].Lecture Notes in ComPuter Science，1997 (1355)：101-109.

[3] 邹艳，陆佩忠.关键方程的新推广[J].计算机学报，2006，29(5)：711-718.

ZOU Yan，LU Peizhong.A new genera1ization of key equation[J].Chinese Journa1 of ComPuters，2006，29(5)：711-718.(in Chinese)

[4] 刘建成，杨晓静.基于求解校验序列的(n，1，m)卷积码盲识别[J].电子与信息学报，2012，34(10)：2363-2368.

LIU Jiancheng，YANG Xiaojing.B1ind recognition of(n，1，m)convo1utiona1 code based on so1ving check-sequence[J].Journa1 of E1ectronics&Information Techno1-ogy，2012，34(10)：2363-2368.(in Chinese)

[5] 杨晓静，刘建成，张玉.基于求解校验序列的(n，k，m)卷积码盲识别[J].宇航学报，2013，2013(4)：568-573.

YANG Xiaojing，LIU Jiancheng，ZHANG Yu.B1ind recognition of(n，k，m)convo1utiona1 codes based on so1ving check-sequence[J].Journa1 of Astronautics，2013，2013 (4)：568-573.(in Chinese)

[6] WANG F H，HUANG Z T，ZHOU Y.A method for b1ind recognition of convo1ution code based on Euc1idean a1gorithm[C]//Proceedings of 2007 Internationa1 Conference on Wire1ess Communications Networking and Mobi1e ComPuting.Shanghai：IEEE，2007：1414-1417.

[7] XIE H，CHAI X M，WANG F H，et a1.A method for b1ind identification of rate 1/2 convo1utiona1 code based onImProved euc1idean a1gorithm[C]//Proceedings of 2012 Internationa1 Conference on Signa1 Processing Proceedings.Beijing：IEEE，2012：1307-1310.

[8] MARAZIN M，GAUTIER R，BUREL G.Dua1 code method

for b1ind identification of convo1utiona1 encoder for cognitive radio receiver design convo1utiona1 encoder for cognitive radio receiver design[C]//Proceedings of 2009 GLOBECOM.Hono1u1u，Hawaii，USA：IEEE，2009：1-6.

[9] DINGEL J，HAGENAUER J.Parameter estimation of a convo1utiona1 encoder from noisy observations[C]//Proceedings of 2007 IEEE Internationa1 SymPosium on Information Theory.Nice：IEEE，2007：1776-1780.

[10] BARBIER J，SICOT G，HOUCKE S.A1gebraic aPProach for the reconstruction of 1inear and convo1utiona1 error correcting codes[J].Internationa1 Journa1 of APP1ied Mathematics and ComPuter Sciences，2006，2(3)：113-118.

[11] 张立民，刘杰，钟兆根.(n，1，m)递归系统卷积码的盲识别[J].电讯技术，2014，54(9)：1220-1225.

ZHANG Limin，LIU Jie，ZHONG Zhaogen.B1ind recognition of(n，1，m)recursive system convo1utiona1 code [J].Te1ecommunication Engineering，2014，54(9)：1220-1225.(in Chinese)

[12] 陆佩忠，沈丽，邹艳.删除卷积码的盲识别[J].中国科学，2005，35(2)：173-185.

LU Peizhong，SHEN Li，ZOU Yan.B1ind recognition of Punctured convo1utiona1 codes[J].Science in China Series E-Information Sciences，2005，35(2)：173-185. (in Chinese)

[13] CLUZEAU M，FINIASZ M.Reconstruction of Punctured convo1ution codes[C]//Proceedings of 2009 IEEE Information Theory WorkshoP.Seou1，Korea：IEEE，2009：546-550.

[14] MARAZIN M，GAUTIER R，BUREL G.A1gebraic method for b1ind recovery of P unctured convo1utiona1 encoders from an erroneous bitstream[J].Institution of Engineering and Techno1ogy，2012，6(2)：122-133.

[15] SHEN B Z，PATAPOUTIAN A，MCEWEN P A.Punctured recursive convo1utiona1 encoders and their aPP1ications in turbo codes[J].IEEE Transactions on Information Theory，2001，47(6)：2300-2320.

[16] 陈发新.删除卷积码生成矩阵及最佳信息恢复式的求法[J].无线电通信技术，2009(2)：5-10.

CHEN Faxin.A deducing method of generator matrix and the bPest information restoration matrix of Punctured convo1utiona1 codes[J].Radio Communications Techno1-ogy，2009(2)：5-10.(in Chinese)

包 昕(1986—)，男，四川成都人，2011年于盲信号处理重点实验室获硕士学位，现为博士研究生，主要研究方向为信道编码和卫星通信；

BAO Xin was born in Chengdu，Sichuan Province，in 1986.He received the M.S.degree from Nationa1 Key Laboratory on B1ind Signa1s Processing in 2011.He is current1y working toward the Ph.D. degree.His research concerns channe1 coding and sate11ite communication.

Emai1：funandaxian@foxmai1.com

游 凌(1971—)，男，成都人，2001年于盲信号处理重点实验室获工学博士学位，主要研究方向为盲信息处理。

YOU Ling was born in Chengdu，Sichuan Province，in 1971.He received the Ph.D.degree from Nationa1 Key Laboratory on B1ind Signa1s Processing in 2001.His research concerns b1ind signa1 Processing.

Emai1：YouLing2001@163.com

A Unified Description of Generator Matrix of Expansion Convolutional Codes

BAO Xin，YOU Ling
(Nationa1 Key Laboratory on B1ind Signa1s Processing，Chengdu 610041，China)

In order to get enough Priori know1edge about the exPansion convo1utiona1 codes in the Process of b1ind recognition of Punctured convo1utiona1 codes，a method for describing the unified generator matrix of the mother code and the exPansion convo1utiona1 codes is ProPosed.Through ana1yzing the basic Physic PrinciP1e of the re1ationshiP between the inPut and the outPut of encoding，the method first sets(n，1，m) and(n，k，m)convo1utiona1 codes as the mother code，then constructs a corresPondence coefficient mode1 of the Po1ymerization of the exPansion convo1utiona1 coding，and fina11y introduces and Proves a unified descriPtion theorem about the generator matrix of the exPansion convo1utiona1 codes.The verification shows that the theorem rea1izes the fast comPutation of the exPansion generator matrix and is ab1e to he1P to exhaustive1y search and reconstruct the mother generator matrices and the Puncturing Patterns.

b1ind recognition；Punctured convo1utiona1 codes；mother codes；exPansion convo1utiona1 code；generator matrix

TN911.22

A

1001-893X(2016)03-0267-06

10.3969/j.issn.1001-893x.2016.03.006

2015-08-26;

2015-12-04 Received date:2015-08-26;Revised date:2015-12-04

**通信作者:funandaxian@foxmai1.com Corresponding author:funandaxian@foxmai1.com