一种改进的时不变LDPC卷积码构造方法*

穆丽伟，刘星成

(1. 华南师范大学物理与电信工程学院∥广东省量子调控工程与材料重点实验室，广东 广州510006;2. 中山大学信息科学与技术学院，广东 广州510006)

一种改进的时不变LDPC卷积码构造方法*

穆丽伟1，刘星成2

(1. 华南师范大学物理与电信工程学院∥广东省量子调控工程与材料重点实验室，广东 广州510006;2. 中山大学信息科学与技术学院，广东 广州510006)

提出一种新的时不变LDPC卷积码构造算法。对Tanner等的构造方案进行改进，产生了给定码率下的LDPC卷积码多项式矩阵；根据卷积码特性，对该多项式矩阵进行修正，获得具有最大给定编码记忆和快速编码特性的改进的时不变LDPC卷积码。该算法具有的快速编码特性可以降低硬件实现时的编码复杂度。该算法获得的在给定码率下具有最大给定编码记忆的特性可提高译码性能。对码的特性参数和仿真结果的分析表明，文中构造的时不变LDPC卷积码是优异的。

低密度奇偶校验(LDPC)卷积码；时不变；给定码率；给定编码记忆；快速编码

随着Shannon[1]开创性论文的发表以及Hamming[2]码和Golay[3]码的出现，致力于低复杂度、低延迟以及接近容量的编码理论研究开始蓬勃发展起来。过去20年，主要集中在以图论为基础的编码理论研究上，尤其是turbo码和低密度奇偶校验(LDPC，Low-Density Parity-Check)分组码。用具有低运算复杂度的置信传播算法进行译码，LDPC分组码展现了优异的译码性能。然而，用LDPC分组码进行编码，需要把数据流分成帧进行传递，不适于某些应用[4]。

与分组码不同，卷积码适于基于数据流传输的通信系统。自1999年LDPC卷积码的构造译码算法提出以来[5]，具有随机和结构化特性的LDPC卷积码的构造方法已经成为很多学者关注的研究方向。常利用LDPC分组码获得LDPC卷积码,对LDPC分组码进行拆分重组可获得随机化特性的时变LDPC卷积码[6-9]。根据环同构，可直接用准循环(QC，Quasi-Cyclic) LDPC分组码获得具有结构化特性的时不变LDPC卷积码[10-13]。Tanner等[13]提出了经典的构造时不变LDPC卷积码的算法。他们首先给出一种QC-LDPC码构造算法，然后根据环同构关系，获得了LDPC卷积码的多项式奇偶校验矩阵。与QC-LDPC分组码类似，时不变LDPC卷积码具有占用存储空间小、易于实现的特性。但是Tanner等[13]的构造算法还存在如下不足之处：① LDPC卷积码的编码码率只能根据给定构造参数获得，不能预先给定；② 最大编码记忆只有在获得生成矩阵后才可获知；③ 不具有LDPC卷积码本身固有的优势：快速编码特性[1]。

根据以上分析，本文首先介绍了Tanner等[13]提出的时不变LDPC卷积码构造算法，由该算法的具体构造参数进一步指出其不足之处。然后对该算法进行改进，构造了在给定码率和给定最大编码记忆下，具有快速编码特性的结构化LDPC卷积码的多项式形式奇偶校验矩阵。最后，对所构造的码给出仿真结果并进行性能分析。

1 时不变LDPC卷积码的构造算法

介绍Tanner等[13]提出的LDPC卷积码构造算法，分析其不足之处。

先介绍其构造算法。首先，根据给定的构造参数：非负整数m以及两个参数a、b， 由乘阶O(a)=K，O(b)=J，获得(J,K)多项式矩阵

(1)

其中，J×K矩阵P的第(s,t)个元素Ps,t=atbs(0≤s≤J-1,0≤t≤K-1)。

其次获得矩阵P对应的QC-LDPC分组码矩阵

(2)

其中，Ix是一个行循环左移x位的m×m单位阵。

最后，根据环同构，获得LDPC卷积码多项式矩阵

(3)

其中，D是延时算子，D的幂x即单位阵循环左移的位数x，该LDPC卷积码的码率是(1-J/K)。H(D)称为LDPC卷积码的多项式奇偶校验矩阵[13]。

由构造过程可知，该算法的不足之处在于：① 给定构造参数m和a、b后，才可获知LDPC卷积码的码率(1-J/K)；② 构造前，编码记忆不详(只有得到H(D)对应的生成矩阵G(D)后，才可获悉最大编码记忆[13])；③ 该算法要用高斯消去法从H(D)获得生成矩阵G(D)后，才可对输入信息进行编码获得LDPC卷积码[13]，因此并不具有卷积码特有优势之一：快速编码特性，即不具有由H(D)直接进行编码的特性。

2 时不变LDPC卷积码构造算法的改进

本部分对前述算法进行改进，构造在给定码率和给定最大编码记忆下具有快速编码特性的LDPC卷积码。

首先，获得在给定最大编码记忆和给定码率下的矩阵H(D)。给定最大编码记忆m，可获得参数(J,K)及码率R=(1-J/K)，其中， (J,K)是φ(m)的因子[13]；

根据文献[13]，两个待求的非零整数a、b满足乘阶O(a)=K,O(b)=J，且

(4)

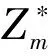
(5)

对码长为K的LDPC卷积码直接进行编码获得J个校验位。其它(K-J)位是输入的信息位，可直接输出[1]。这种可由H(D)直接编码的特殊矩阵形式，称为快速编码特性，是LDPC卷积码的特有优势，可减小编码复杂度。

本文直接把矩阵H(D)最后J列对角线上元素置换为D0，即可获得具有快速编码特性的矩阵结构。根据在相同译码算法下，卷积码译码性能与记忆长度成正比这一特性，直接把H(D)前J列对角线上元素置换为Dm，即可获得每个时刻上的最大编码记忆ms=m，本文里m为给定参数。至此，本文构造了在给定码率(1-J/K)以及给定最大编码记忆m下，具有快速编码特性的LDPC卷积码多项式矩阵，其结构如下

(6)

由(6)式可推知，仅具有快速编码特性的矩阵可表示为

(7)

本文用(m，J，K)表示一个码率为(1-J/K)的LDPC卷积码，其中m为最大编码记忆，J为多项式矩阵HFm(D)的行数，K为列数。本文所有的仿真都是在加性白色高斯噪声(AWGN)信道下，在接收端使用BP(Belief Propagation,置信传播)译码算法，迭代次数为50的编译环境下获得的性能结果。图1给出了(31，3，5)LDPC卷积码在奇偶校验矩阵H(D)、HF(D)以及HFm(D)下的仿真结果。本文中所有图的纵坐标用BER(biterrorrate，误比特率)表示。横坐标用Eb/N0表示，其中Eb是传输每比特(bit)信息所消耗的平均能量，N0/2是AWGN信道上的平均功率谱密度。仿真结果表明，在BER为4×10-7左右，由HFm(D)所获得的LDPC卷积码比由H(D)所获得的码要好1.8dB左右，比HF(D)所获得的码要好1dB左右。其中最主要的原因是经变换后，LDPC卷积码的多项式矩阵结构发生了变化，尤其是环和记忆长度。表1给出了相同构造参数的LDPC卷积码在不同多项式矩阵下的环和记忆长度。表1的特性参数表明，图1中所有 (31,3,5)LDPC卷积码具有相同的girth(最小环长)，但由HFm(D)所获得的码具有最大编码记忆m=31。图2(a)表明，与(122,3,5)LDPC卷积码相比， (26,3,4)LDPC卷积码具有更大的性能增益。表1显示，所有(26,3,4)LDPC卷积码中，由HFm(D)所获得的码具有最大的girth(girth=10)和最大的编码记忆(m=26)。所有(122,3,5)LDPC卷积码的girth相同，但由HFm(D)所获得的码具有最大的编码记忆(m=26)。图2(b)表明，在低信噪比区，推荐的(211,3,5)码具有更好的性能，而在高信噪比区，推荐的码与原码性能几乎相同，由表1可看出，所有(211,3,5)LDPC卷积码中，尽管由HFm(D)所获得的码其记忆长度比原码大，但girth却比原码小。由此可看出，具有相同构造参数的所有LDPC卷积码，在girth(memory)相同的情况下，memory(girth)越大，LDPC卷积码的性能越好；但girth(memory)较小，memory(girth)较大时，在高信噪比区，LDPC卷积码具有相似的性能。经过对大量仿真结果的分析，本文所构造的LDPC卷积码的性能比原码更好或几乎相同，而本文提出的码具有快速编码特性，可大大减小编码复杂度。所以本文构造的码具有优异的特性。

图1 (31，3，5)LDPC卷积码在不同校验矩阵下的仿真结果Fig.1 Simulation results of (31,3,5) LDPC convolutional codes associated with different check matrices

图2 不同构造参数下LDPC卷积码的BER性能Fig.2 The BER performance of LDPC convolutional codes under different construction parameters

表1LDPC卷积码在不同校验矩阵下的特性

Table1ThecharacteristicsofLDPCconvolutionalcodeswithdifferentcheckmatrices

LDPC卷积码H(D)girth/girth数memoryHF(D)girth/girth数memoryHFm(D)girth/girth数memory(26，3，4)8/94258/132510/1226(31，3，5)8/190288/85258/4931(122，3，5)10/26811910/6711910/138122(151，3，5)10/741188/11188/71151(211，3，5)12/88020110/9620110/49211

3 仿真结果

本部分构造本文提出的 (151,3,5)LDPC卷积码并对其进行仿真，仿真结果见图3。由图3可知，在BER为4×10-6左右，具有矩阵HFm(D)的(151,3,5)LDPC卷积码比文 [6] 中所构造的(209,3,5)FE-I型(见文[6]Fig.1的FE-ICC曲线)LDPC卷积码好0.1dB左右，比Tanner等[13]所构造的 (187,3,5)(见文[12]Fig. 12的R=2/5convcode,ms=187曲线)的LDPC卷积码好0.2dB左右，与文献[14]中的(204,3,5)码(见文[14]Fig.9的m=204,ms=204曲线)性能几乎相同(图3中所有用于比较的码性能均复制于对应的文献中)。该仿真结果表明，与其他构造算法相比，在相同码率R下，要获得同样的BER，该改进构造算法需要更小的记忆。值得注意的是该改进的构造还具有快速编码特性，可减小编码复杂度。

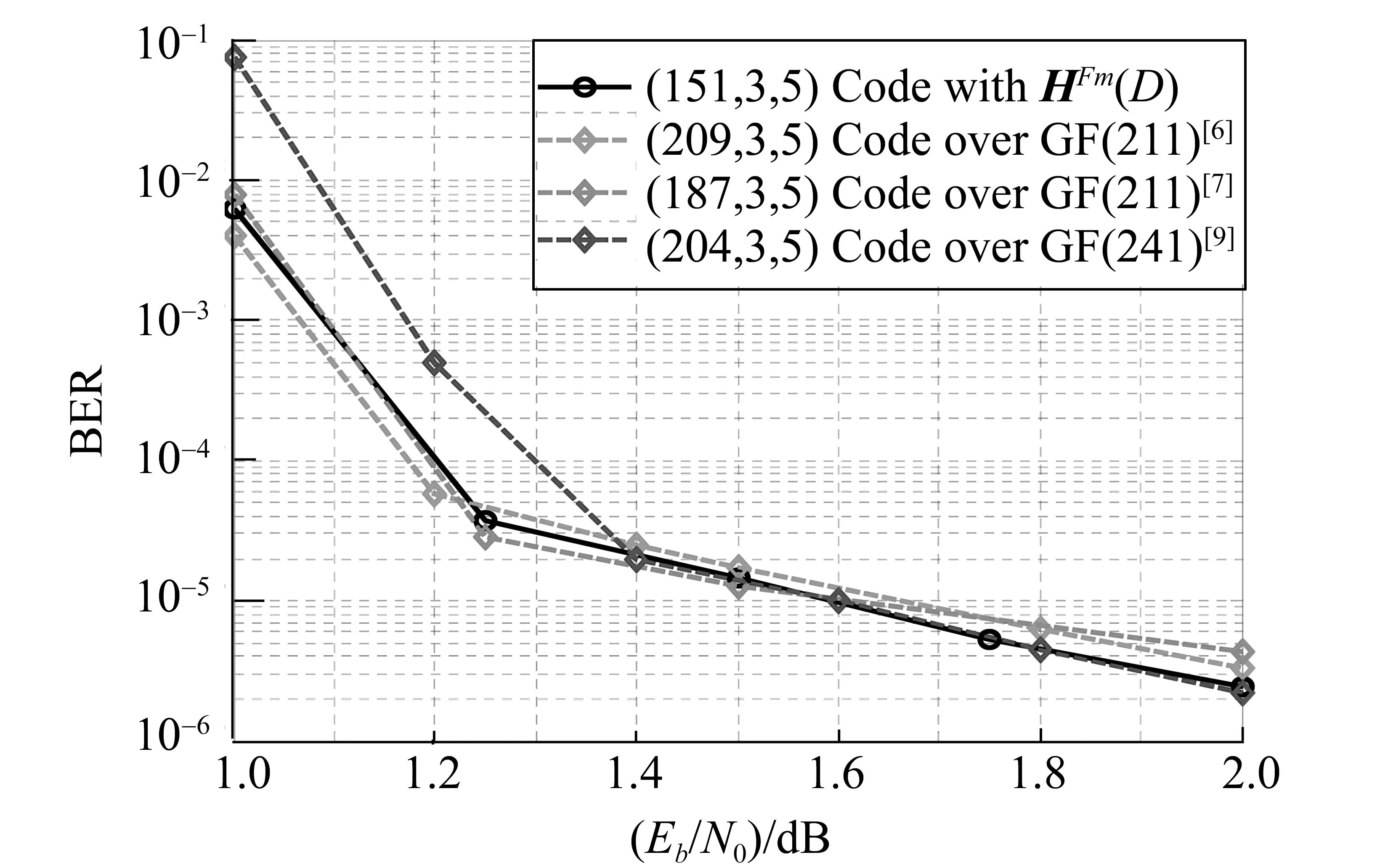
图3 几种LDPC卷积码的仿真结果Fig.3 Several simulation results of LDPC convolutional codes

4 结 语

本文提出了一种新的LDPC卷积码的构造算法。新的算法首先获得在给定码率下的结构化LDPC卷积码。然后根据快速编码特性可以简化编码复杂度；在同样的译码算法下，记忆越大性能越好这两个卷积码特有的属性，本文进一步构造了具有快速编码特性和最大给定编码记忆的LDPC卷积码多项式矩阵。对码进行的特性分析和给出的仿真结果表明，该算法是优异的。

[1]SHANNONCE.Amathematicaltheoryofcommunication[J].BellSystemTechnicalJournal, 1948, 27: 379-423, 623-656.

[2]HAMMINGRW.Errordetectinganderrorcorrectingcodes[J].BellSystemTechnicalJournal, 1950, 26(2): 147-160.

[3]GOLAYMJE.Notesondigitalcoding[J].ProceedingsofIRE, 1949, 37: 657.

[4]COSTELLODJJr,PUSANEAE,BATESS,etal.AcomparisonbetweenLDPCblockandconvolutionalcodes[C]∥ProceedingsofInformationTheoryandApplicationsWorkshop,SanDiego,CA,USA, 2006.

[5]JIMENEZFA,ZIGANGIROVKS.Time-varyingperiodicconvolutionalcodeswithlow-densityparity-checkmatrix[J].IEEETransactionsonInformationTheory, 1999, 45(6): 2181-2191.

[6]BOCHAROVAIE,KUDRYASHOVBD,JOHANNESSONR.SearchingforbinaryandnonbinaryblockandconvolutionalLDPCcodes[J].IEEETransactionsonInformationTheory, 2015,1-1:99.

[7]MULW,LIUXC,LIANGCL.ImprovedconstructionofLDPCconvolutionalcodeswithsemi-randomparity-checkmatrices[J].ScienceChinaInformationScience, 2014, 57(2): 022304:1-022304:10.

[8]GROSJEANL,RASMUSSENLK,THOBABENR,etal.SystematicLDPCconvolutionalcodes:asymptoticandfinite-lengthanytimeproperties[J].IEEETransactionsonCommunications, 2014, 62(12): 4165-4183.

[9]ZHOUHua,GOERTZN.RecoverabilityofvariablenodesinperiodicallypuncturedLDPCconvolutionalcode[J].IEEECommunicationsLetters, 2015, 19(4): 521-524.

[10]KUDEKARS,RICHARDSONT,URBANKERL.Spatiallycoupledensemblesuniversallyachievecapacityunderbeliefpropagation[J].IEEETransactionsonInformationTheory, 2013, 59(12): 7761-7813.

[11]MULW,LIUXC,LIANGCL.ConstructionofLDPCconvolutionalcodesoverfinitefields[J].IEEECommunicationsLetters, 2013, 16(6): 897-900.

[12]BALDIM,CANCELLIERIG,CHIARALUCEF.Arrayconvolutionallowdensityparity-checkcodes[J].IEEECommunicationsLetters, 2014, 18(2): 336-339.

[13]TANNERRM,SRIDHARAD,SRIDHARANA,etal.LDPCblockandconvolutionalcodesbasedoncirculantmatrices[J].IEEETransactionsonInformationTheory, 2004,IT-50(12): 2966-2984.

[14]ZHOUH,GOERTZN.Girthanalysisofpolynomial-basedtime-invariantLDPCconvolutionalcodes[C]∥InternationalConferenceonSystems,SignalsandImageProcessing,Vienna,Austria, 2012: 104-108.

Construction of time-invariant LDPC convolutional codes with modified method

MULiwei1,LIUXingcheng2

(1. Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials∥ School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China；2. Department of Electronic and Communications Engineering, Sun Yat-sen University,Guangzhou 510006, China)

A novel approach of constructing time-invariant LDPC convolutional codes is proposed. The matrix of an LDPC (Low-Density Parity-Check) convolutional code with a given rate is generated according to the original matrix generated by Tanner etc. Then, the matrix with maximum given encoding memory and fast encoding property is obtained by modifying the above-mentioned matrix. The fast encoding property of the proposed matrix can reduce the encoding complexity. And the maximum given encoding memory of the proposed LDPC convolutional code can improve the decoding performance. The characteristic parameters and simulation results show that the proposed LDPC convolutional codes are excellent .

LDPC convolutional codes; time-invariant; given rate; given memory; fast encoding

10.13471/j.cnki.acta.snus.2016.01.011

2015-03-28

国家自然科学基金资助项目(61401164，61173018)；广东省自然科学基金资助项目(2014A030310308)

穆丽伟(1980年生)，女；研究方向：信道编码与无线通信；E-mail:liweimuscnu@163.com

TN

A

0529-6579(2016)01-0063-05