基于Benford律的Logistic模型及其在财务舞弊识别中的应用

杨贵军，周亚梦，孙玲莉，石玉慧

(天津财经大学 统计学院，天津 300222)

一、引言

近年来，尽管政府监管不断加大对上市公司财务舞弊的惩罚力度，财务舞弊事件仍然屡屡发生，干扰了正常的市场经济秩序，损害了广大投资者的利益。财务舞弊的原因非常复杂，舞弊手段也不断更新，更加有效的财务舞弊识别新方法仍是当前关注的热点。

Benford律是舞弊识别的常用方法之一，指大量自然数据集中首位数字的分布规律。如果某财务指标的首位数字分布与Benford律不一致，则认为该财务指标的舞弊风险高，数据受到人为操纵的可能性较大[1]。在会计、税务、审计等领域，Benford律已被用于识别财务数据是否有修饰、篡改与舞弊等问题。Nigrini等最早提出将Benford律用于财务舞弊识别并应用到会计、税务等领域，成功识别出大量舞弊案例[2-3]。Carslaw、Thomas先后使用Benford律识别出新西兰和美国的会计净利润数据的人为操纵行为及特征[4-5]。Aris等识别出马来西亚公共部门的会计欺诈风险[6]。张苏彤等验证了Benford律对中国上市公司的财务数据具有适用性，提出可将Benford律作为查找上市公司财务舞弊征兆的工具[7]。朱文明等进一步给出了应用Benford律进行舞弊审计的操作步骤和分析流程[8]。然而，以上所有学者对Benford律的研究仅限于评价财务数据整体质量。虽然Benford律可以检测数据质量低的财务指标，确定异常数据范围，但无法识别出具体的舞弊样本点，而识别舞弊样本点对于审计实务具有更重要意义。

实质上，财务舞弊识别往往被看做二分类问题，很多财务舞弊识别模型都来源于Logistic模型[9-11]。Mscore模型和Fscore模型是西方资本市场常用的财务舞弊识别模型。Mscore模型选择财务指标作为解释变量，建立Logistic模型，成功预测出美国安然公司的财务舞弊[9]。Fscore模型在Mscore模型基础上，从应计项、财务指标、非财务指标、表外业务和市场信息五个方面选择解释变量，建立预测财务舞弊的Logistic模型，识别出美国在1990年和2000年互联网泡沫期间的财务舞弊公司最多[10]。钱苹等利用中国上市公司财务指标，基于Mscore模型和Fscore模型，建立适合中国资本市场的Cscore财务舞弊识别Logistic模型[11]。已有使用Logistic模型识别财务舞弊的研究仅关注财务指标，并未关注这些指标的数据质量。

财务指标真实可信是Logistic模型成立的前提条件之一。根据Benford律分布一致性检验原理，如果财务指标的首位数字分布与Benford律之间差异显著，说明财务指标受到人为操纵的可能性大，不能直接使用这些财务指标建立Logistic模型。否则，建立的Logistic模型结论的合理性将受到质疑。为此，本文提出将Benford律和Logistic模型结合的一种舞弊识别方法。新方法首先基于Benford律生成一组可以反映财务指标数据质量并标记潜在异常样本点的变量，称为Benford因子，然后将Benford因子作为新解释变量引入Logistic模型中，改善Logistic模型拟合效果，提高舞弊识别的正确率。基于中国上市公司财务数据的模拟显示，包含Benford因子的Logistic模型往往具有更高的正确率，识别财务舞弊样本点的正确率也高于普通Logistic模型。

二、带有Benford因子的Logistic模型

(一)Benford律

Benford律是指在大量自然数据集中首位数字的频率分布呈单调下降趋势的一种对数规律[12]。Hill给出Benford律的统计解释[13]。记d=1，2，…，9，首位数字D为d的概率为：

fB，d=log10(1+1/d)

(1)

现有的理论研究和实证分析显示，大量财务数据的首位数字都服从Benford律，舞弊行为往往会导致财务数据不符合Benford律[2]。财务数据中首位数字分布规律与Benford律之间差异显著，意味着财务数据质量低，存在弄虚作假、修饰、篡改等风险。检验首位数字的概率分布是否服从Benford律的方法主要有四种：χ2拟合优度检验、修正K-S拟合优度检验、距离检验和Pearson相关系数检验[14]。χ2拟合优度检验是最常用的方法。记N为样本量，fd为待检验财务数据的首位数字d(d=1，2，…，9)出现频率。χ2拟合优度检验统计量为：

(2)

给定显著性水平，如果χ2检验统计值大于临界值，拒绝原假设，认为财务数据集中首位数字出现频率不符合Benford律。数据集中首位数字分布与Benford律比较，只能给出数据质量的总体评价，很难识别某个具体样本点是否存在舞弊问题[15]。

(二)基于Benford律的Benford因子构造

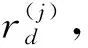
(3)

(4)

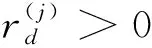
(5)

构造指标Xj(j=1，2，…，k)的Benford因子，记为Bj。若样本点p的指标xj，p的首位数字为a(j)，则Bj取值为1；否则，Bj取值为0，即：

(6)

注意，Bj因子可能与其他Benford因子之间存在交互效应，需要根据实际情况选择。

(三)Benford-Logistic模型

Benford因子及其交互效应提供了样本点的数据质量信息。本文将包含Benford因子的Logistic模型称为Benford-Logistic模型。财务舞弊识别的Logistic模型中涉及的财务指标一般为财务比率指标，是根据同一时期财务报表中两个或多个项目之间的关系，计算其比率。比率指标用相对数表示。总量指标是用来反映上市公司财务总规模或总水平的统计指标，用绝对数表示，是计算比率指标的基础指标。Benford律对这两类财务指标的数据质量评价效果有所不同。实际上，如果总量指标存在舞弊问题，经过运算得到的比率指标可能满足Benford律。这是因为数据在运算过程中往往过滤掉大量信息，其中可能包括舞弊信息，降低了Benford律对比率指标的舞弊识别效果。这里，Benford因子包括总量指标Benford因子和比率指标Benford因子。假设因变量Y表示是否为财务舞弊公司，财务舞弊公司记为1，非财务舞弊公司记为0。解释变量为财务指标，记为Xi(i=1，2，…，m，m≥k)。普通Logistic模型为：

ln{P(Y=1|X)/[1-P(Y=1|X)]}

=β0+β1X1+β2X2+…+βmXm

(模型Ⅰ)

包含总量指标Benford因子的Benford-Logistic模型为：

ln{P(Y=1|X，B)/[1-P(Y=1|X，B)]}

(模型Ⅱ)

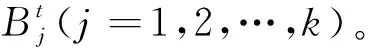
ln{P(Y=1|X，B)/[1-P(Y=1|X，B)]}

(模型Ⅲ)

采用Benford-Logistic模型识别财务舞弊公司的主要步骤如下：

1.对所有待检验财务指标数据集，采用Benford律进行显著性检验，识别出数据质量低的财务指标Xj(j=1，2，…，k)。

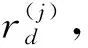
3.将比率指标的Benford因子或总量指标的Benford因子加入到Logistic模型中，构建比率指标Benford-Logistic模型或总量指标Benford-Logistic模型，对公司进行财务舞弊识别。

本文提出的Benford-Logistic模型保留了Benford律能有效评价数据质量、Logistic模型分类准确率高的优点，增加Benford因子也提高了Logistic模型的正确率。

三、中国上市公司财务舞弊识别的模拟研究

下面基于中国上市公司财务数据，利用Benford-Logistic模型识别财务舞弊的上市公司。

(一)变量选择与数据来源

现有上市公司财务舞弊的研究文献，主要是从舞弊动因、偿债能力、盈利能力、现金流量、营运能力五个方面考虑影响上市公司财务舞弊行为的财务指标[9，16]。衡量舞弊动因的代表性指标是舞弊前三年平均ROE∈(6%，7%)和管理层持股比例。在中国证券市场安排机制下，舞弊前三年平均ROE在(6%，7%)的上市公司处于配股边界，出于增发配股的需要，其财务舞弊可能性较大。管理层持股比例增加，管理层对企业的控制力就会不断增强，外部约束力被削减，更容易发生财务舞弊。公司偿债能力的代表性指标是流动比率和速动比率，反映公司通过资产变现短期偿还债务的能力。盈利能力的代表性指标为ROA和ROE，反映公司对投入资金的运作回报能力。现金流量的代表性指标是现金流量比率和每股现金流量，反映公司现金流动性与获取现金的能力。营运能力的代表性指标是存货周转率、资产周转率、应收账款周转率，评价公司运用存货、总资产、应收账款等各项资产赚取利润的能力。一般而言，偿债能力越弱、盈利能力越弱、流动性与获取现金能力越弱、营运能力越弱，公司舞弊可能性越高。具体变量定义如表1所示。

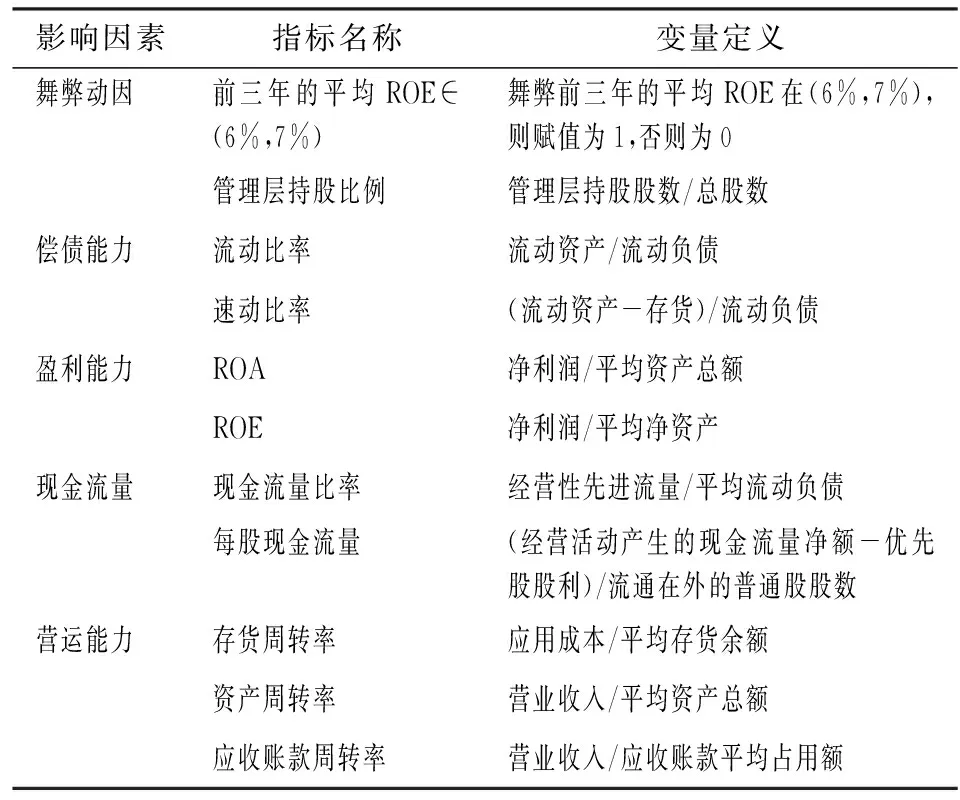
表1 财务舞弊识别指标

选取因财务舞弊受到证监会、上交所、深交所和财政部处罚的A股上市公司作为舞弊公司样本，响应变量Y取值为1。没有因财务舞弊受到公开处罚的A股上市公司作为非舞弊公司样本，响应变量Y取值为0。中国从2005年开始实行股权分置改革，因此本文将样本区间确定为2006—2017年。剔除金融行业、关键数据缺失和上市不足3年的上市公司后，共收集到158个舞弊公司样本、4 115个非舞弊公司样本。相关数据来源于锐思金融数据库(RESSET)。

基于相关系数检验和VIF检验，部分变量存在较强的相关性。采用AIC准则和变量显著性等识别办法对解释变量进行筛选，最终保留了重要且显著的2个财务指标变量：ROA和现金流量比率。由表1可知，构成比率指标ROA的总量指标有净利润和资产总额，构成比率指标现金流量比率的总量指标有经营性现金流量和流动负债。相关统计描述见表2。

表2 变量说明、描述性统计与χ2拟合优度检验

(二)Benford因子的构造

为了构造表征财务舞弊的Benford因子，先对财务指标进行Benford律显著性检验。检验的指标包括4个总量指标，分别为净利润、资产总额、经营性现金流量、流动负债；2个比率指标，分别为ROA、现金流量比率。各指标首位数字观测频率与Benford律下理论频率差异的χ2拟合优度检验结果见表2的最后1列。表2的χ2拟合优度检验结果显示，只有流动负债指标的χ2检验值为8.36，小于显著性水平10%下的临界值13.36，表明流动负债数据首位数的分布规律与Benford律较为一致。其他指标的χ2检验值高，说明这些指标可能存在数据质量问题。计算每个指标首位数字的观测频率与Benford律下理论频率之间差值，结果见表3。

表3显示，流动负债指标的首位数字分布较好服从Benford律，与Benford律下理论频率之间差异小。其他指标的首位数字观测频率与Benford律下理论频率之间差异大。ROA、现金流量比率、净利润、资产总额、经营性现金流量等指标，观测频率与Benford律下理论频率偏差最大的首位数字分别是4、2、3、7、1，观测频率比Benford律下理论频率分别高出2.07%、2.44%、1.38%、1.18%、0.98%。构造与上述指标相对应的Benford因子，然后根据式(6)对样本点的Benford因子赋值。

表3 指标首位数字的观测频率与

(三)Benford-Logistic模型正确率分析

考虑到模拟结果的稳定性和数据不平衡会降低模型的拟合效果，本文对正常公司样本进行1 000次不放回抽取，每次抽取158个样本点，然后与舞弊公司样本点合并，构成容量为316的1 000组样本。

为了比较三个模型的优劣，计算每个模型的正确率、第一类错误率、第二类错误率和最优频数。表4给出每个模型分类结果的四种情形。记n=a11+a12+a21+a22。正确率等于实际舞弊的公司被判断为舞弊公司以及实际正常的公司被判断为正常公司的比例，即正确率为(a11+a22)/n。第一类错误率是将正常公司错判为舞弊公司的概率，即第一类错误率为a21/(a21+a22)。第二类错误率是将舞弊公司错判为正常公司的概率，即第二类错误率为a12/(a11+a12)。最优频数是在1 000次模拟中某模型的正确率最大的频数、第一类错误率最小的频数和第二类错误率最小的频数[17]。

表4 分类矩阵(样本数为n)

基于全部样本构建模型，分别利用普通Logistic模型、基于总量指标的Benford-Logistic模型和基于比率指标的Benford-Logistic模型进行舞弊公司识别。模型分类结果受阈值影响，为了便于模型比较，将阈值统一设定为0.5。分别依据上述三个模型对样本类别进行判断，比较分类结果与真实类别，计算正确率、第一类错误率、第二类错误率和最优频数。

图1、图2、图3分别给出了三个模型1 000次结果的正确率和第一类错误率、第二类错误率的箱线图。图中的3个箱线图从左到右依次为Logistic模型、基于总量指标的Benford-Logistic模型和基于比率指标的Benford-Logistic模型。图1显示，三个模型1 000次结果的正确率中位数分别为57.59%、59.18%、59.18%。模型Ⅱ和模型Ⅲ的正确率中位数相等，都高于模型Ⅰ。图2显示，三个模型1 000次结果的第一类错误率中位数分别为44.94%、43.67%、42.41%。模型Ⅲ的第一类错误率中位数低于模型Ⅱ和模型Ⅰ。模型Ⅱ的第一类错误率中位数低于模型Ⅰ。图3显示，三个模型1 000次结果的第二类错误率中位数分别为39.87%、37.34%、39.24%。模型Ⅱ的第二类错误率中位数低于模型Ⅲ和模型Ⅰ。模型Ⅲ的第二类错误率中位数低于模型Ⅰ。

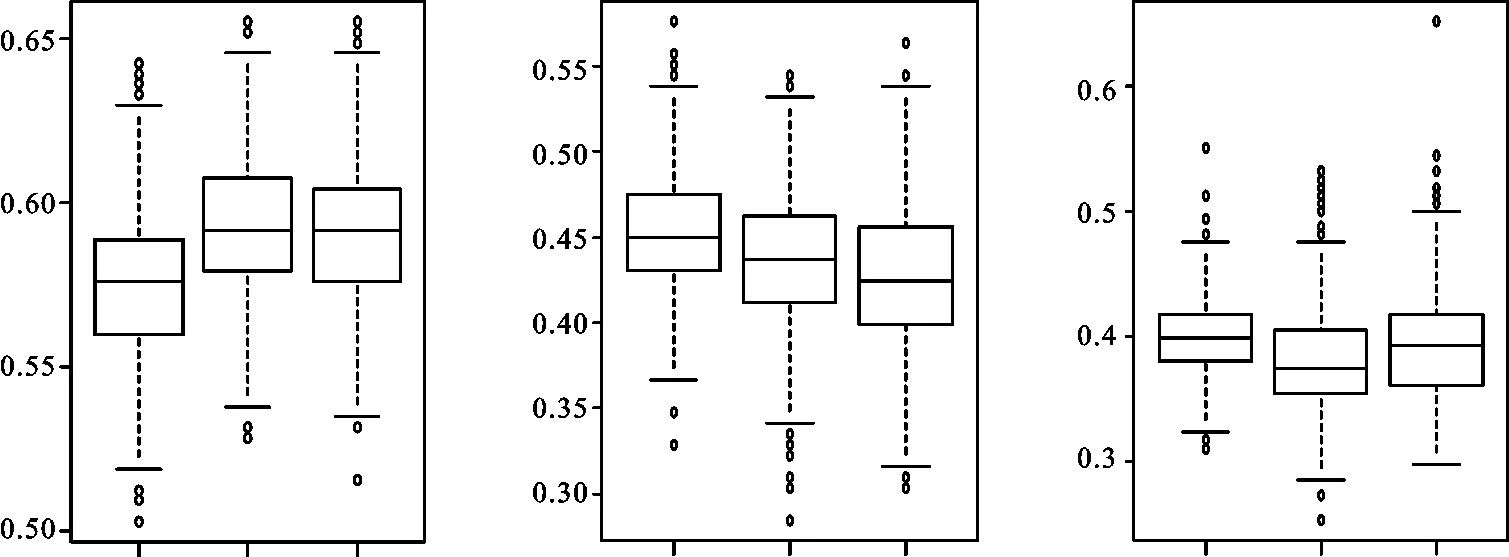
图1 回判正确率图 图2 第一类错误率图 图3 第二类错误类图

表5的第2至4行分别给出三个模型1 000次模拟的平均正确率、平均第一类错误率、平均第二类错误率，5至7行给出三个模型在1 000次模拟中的正确率最高、第一类错误率最低、第二类错误率最低的频数。表5显示，三个模型1 000次结果的平均正确率分别为57.49%、59.26%、59.12%。平均正确率最高的模型是模型Ⅱ，其次是模型Ⅲ，最低的是模型Ⅰ。三个模型1 000次结果的平均第一类错误率分别为45.02%、43.46%、42.64%。平均第一类错误率最低的模型是模型Ⅲ，其次是模型Ⅱ，最高的是模型Ⅰ。三个模型1 000次结果的平均第二类错误率分别为40.01%、38.03%、39.12%。平均第二类错误率最低的模型是模型Ⅱ，其次是模型Ⅲ，最高的是模型Ⅰ。表5显示，在1 000次模拟中三个模型的正确率最高的频数分别为86、500和476，模型Ⅱ的正确率的最优频数最大，达到500次，模型Ⅲ的正确率最高的频数为476次，略低于模型Ⅱ，但高于模型Ⅰ。在1 000次模拟中三个模型第一类错误率最低的频数分别为146、394和541，模型Ⅲ的第一类错误率最低的频数最大；模型Ⅱ的第一类错误率最低的频数为394次，低于模型Ⅲ，但高于模型Ⅰ。在1 000次模拟中三个模型的第二类错误率最低的频数分别为197、536和346，模型Ⅱ的第二类错误率最低的频数最大，达到536次；模型Ⅲ的第二类错误率最低的频数为346次，低于模型Ⅱ，但高于模型Ⅰ。相比较而言，模型Ⅲ针对正常公司的正确率优于模型Ⅰ和模型Ⅱ。模型Ⅱ的正确率和第二类错误率优于模型Ⅰ和模型Ⅲ。尤其对于舞弊公司，模型Ⅱ的识别效果明显优于模型Ⅰ。模型Ⅲ和模型Ⅱ的正确率差异小，二者都明显优于模型Ⅰ。

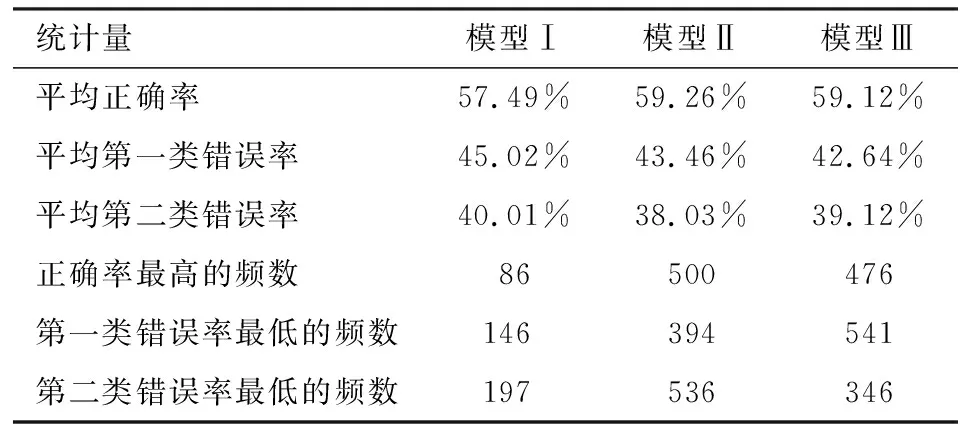
表5 分类准确性和最优频数统计

注：若出现模型正确率相等的情况，按照每个模型都是最优模型统计频数。这里最优频数之和不一定等于总模拟次数1 000。

综上所述，针对舞弊识别的二分类问题，Benford-Logistic模型的正确率往往高于普通Logistic模型。其中，基于总量指标的Benford-Logistic模型识别舞弊公司的正确率优于基于比率指标的Benford-Logistic模型。基于比率指标的Benford-Logistic模型识别正常公司的正确率优于普通Logistic模型和基于总量指标的Benford-Logistic模型。

(四)Benford-Logistic模型与Logistic模型正确率的进一步比较

对于上市公司财务舞弊问题，将财务舞弊公司识别为正常公司会造成更严重的损失，需要严格控制第二类错误率。模型Ⅱ在三个模型中犯第二类错误率的频率最低。为此，下文进一步比较模型Ⅰ和模型Ⅱ的正确率。

在1 000次模拟中，模型Ⅱ的正确率高于模型Ⅰ的频数为806次，占总模拟次数的80.6%。为了进一步比较模型Ⅱ和模型Ⅰ的性质，将806次模拟结果分类，按照第一类错误率的分组结果见表6的1至3列，按照第二类错误率的分组结果见表6的4至6列。表6第1列表示模型Ⅰ与模型Ⅱ的第一类错误率差值，第2列给出模型Ⅱ的第一类错误率低于模型Ⅰ的频数，第3列给出了相应比率。第4列给出模型Ⅰ与模型Ⅱ的第二类错误率差值，第5列给出了模型Ⅱ的第二类错误率低于模型Ⅰ的频数，第6列给出了相应比率。表6显示，在模型Ⅱ的正确率高于模型Ⅰ的806次模拟中，模型Ⅱ的第一类错误率低于模型Ⅰ的频数是612次，比率为75.93%，模型Ⅱ的第二类错误率低于模型Ⅰ的频数是618次，比率为76.67%。模型Ⅱ的正确率高于模型Ⅰ的情况下，模型Ⅱ的第一类错误率和第二类错误率往往低于模型Ⅰ。

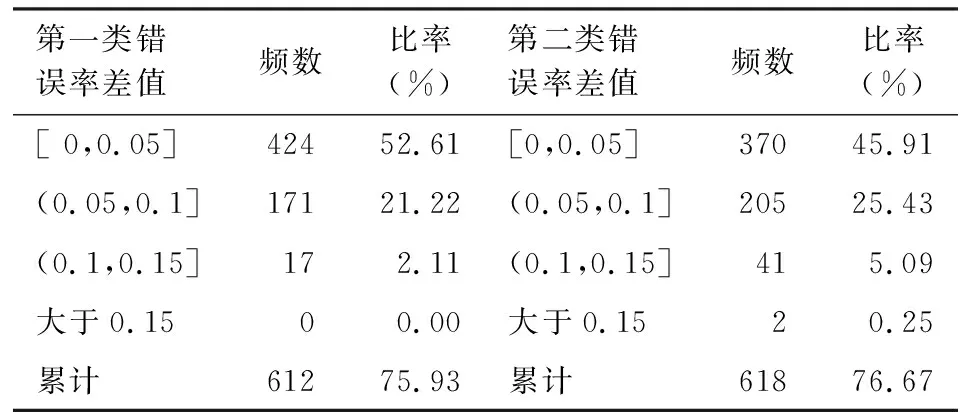
表6 模型Ⅱ的正确率高于模型Ⅰ的情况(总频数为806)

在1 000次模拟中，模型Ⅱ的第一类错误率低于模型Ⅰ的频数为691次，占模拟总次数的69.1%。将691次模拟结果进行分组，按照第二类错误率的分组结果见表7的第1至3列，按照正确率的分组结果见表7的第4至6列。表7的第1列表示模型Ⅰ与模型Ⅱ的第二类错误率差值，第2列给出了模型Ⅱ的第二类错误率低于模型Ⅰ的频数，第3列给出了相应比率。第4列表示模型Ⅱ与模型Ⅰ的正确率差值，第5列给出了模型Ⅱ的正确率高于模型Ⅰ的频数，第6列给出了相应比率。表7显示，在模型Ⅱ的第一类错误率低于模型Ⅰ的691次模拟中，模型Ⅱ的第二类错误率低于模型Ⅰ的频数达到424次，占比为61.36%。模型Ⅱ的正确率高于模型Ⅰ的频数是612次，占比为88.57%。在模型Ⅱ的第一类错误率优于模型Ⅰ的情况下，模型Ⅱ的第二类错误率和正确率往往优于模型Ⅰ，且正确率高的情况更多。

表7 模型Ⅱ的第一类错误率低于模型Ⅰ的情况(总频数为691)

在1 000次模拟中，模型Ⅱ的第二类错误率低于模型Ⅰ的次数达到692次，占模拟总次数的比率为69.2%。将692次模拟结果进行分组，按照第一类错误率的分组结果见表8的1至3列，按照正确率的分组结果见表8的4至6列。表8的第1列表示模型Ⅰ与模型Ⅱ的第一类错误率差值，第2列给出模型Ⅱ的第一类错误率低于模型Ⅰ的频数，第3列给出了相应比率。第4列表示模型Ⅱ与模型Ⅰ的正确率差值，第5列给出模型Ⅱ的正确率高于模型Ⅰ的频数，第6列给出了相应比率。表8显示，在模型Ⅱ的第二类错误率低于模型Ⅰ的692次模拟中，模型Ⅱ的第一类错误率低于模型Ⅰ的频数是424次，占比为61.27%。模型Ⅱ的正确率高于模型Ⅰ的频数是618次，占比为89.31%。模型Ⅱ的第二类错误率优于模型Ⅰ的情况下，模型Ⅱ的第一类错误率和正确率往往高于模型Ⅰ，且正确率高的情况更多。

表8 模型Ⅱ的第二类错误率低于模型Ⅰ的情况(总频数为692)

综上所述，通过模型Ⅱ和模型Ⅰ的正确率、第一类错误率和第二类错误率比较显示，模型Ⅱ的第一类错误率或第二类错误率较低，相应的正确率往往较高。模型Ⅱ的正确率高于模型Ⅰ的情况下，模型Ⅱ的第一类错误率和第二类错误率往往较低。

四、结论

舞弊识别是财务审计监督领域的重要问题。现有文献大多单独使用Benford律、Logistic模型进行财务舞弊识别，少有研究将两种方法组合到一个模型中用于舞弊识别。Benford律的局限在于无法从一组数据中识别出具体的舞弊样本点，而Logistic模型参数估计容易受到解释变量数据质量的影响，降低Logistic模型的正确率。有鉴于此，本文提出Benford律和Logistic模型相结合的财务舞弊识别新方法。首先，利用Benford律评估解释变量的数据质量。然后，选择没有通过Benford律检验的财务指标，计算首位数字的观测频率，确定与理论频率差异最大的首位数字。根据样本数据首位数字与该首位数字是否相等，构造Benford因子作为新的解释变量。最后，将Benford因子加入Logistic模型，进行舞弊识别。中国上市公司财务舞弊数据分析结果显示，在Logistic中加入总量指标的Benford因子或比率指标的Benford因子都能够提高正确率。基于总量指标构造的Benford因子对降低第二类错误率更有效。本文提出的新方法为舞弊识别提供了新思路，能够更好满足审计实务的需求。