基于倾向性得分匹配法的平均处理效应的自助法推断
2019-09-20彭非,吴浩
彭 非,吴 浩
(中国人民大学 a.应用统计科学研究中心;b.统计学院,北京 100872)
一、背景介绍
平均处理效应(average treat effect,以下简称ATE)是评价处理对结果的影响效应的度量,目前广泛应用于生物制药的药效评价,医院治疗方案的疗效评估及公共政策的影响研究等领域。根据反事实结果概念,每个个体只可能具有接受处理的反事实结果Y(1),或者接受对照的反事实结果Y(0),则实际观测值Y可表示为:
Y=ZY(1)+(1-Z)Y(0)
其中Z取1表示处理,取0表示对照,那么ATE的估计为:
K-近邻匹配法是估计ATE的常见方法,但Abadie和Imbens指出在固定匹配个数时,基于协变量欧氏距离匹配法的ATE估计是有偏估计[1]。为此,Abadie和Imbens提出了基于非参数序列回归法的偏差校正匹配估计法[2]。然而,欧氏距离等基于协变量距离的匹配法无法规避维数灾难问题,为此,通常采用倾向性得分法代替协变量距离以实现高维协变量情形的匹配[3]。同时,刘凤芹和马慧指出倾向性得分匹配法具有对误差分布不敏感,以及当公共支撑域较大时对具体匹配方法选择不敏感的优点[4]。Abadie和Imbens证明了基于倾向性得分匹配法的ATE估计的大样本性质,但是方差的渐近表达式形式复杂,程序实现难度较高,且据作者了解目前还没有现成程序包能够直接实现其正确方差估计式,这极大影响了倾向性得分匹配法在实际工作中的使用[5]。
当估计量的理论方差表达式较复杂时,自助法(bootstrap)是方差估计的有效替代方法[6]。但是,Abadie和Imbens通过例子证明了当固定匹配个数时,由于第i个个体的被匹配次数KM(i)在bootstrap样本中不是原样本的一致估计,因此经典的自助法无法直接用于固定匹配个数时匹配法下ATE的统计推断,该结论对固定匹配个数时的任何匹配法(不论是协变量的距离匹配法还是倾向性得分匹配法)均成立,并且猜测可以尝试wild bootstrap[7]。Otsu和Rai在固定匹配个数的协变量欧氏距离匹配法场合下证实了关于wild bootstrap的可行性猜测,并将其权重条件进一步放宽,提出加权自助法并证明了所得估计量的分布收敛于Abadie和Imbens所得估计的分布[8]。但是对于倾向性得分匹配法如何正确使用自助法目前还没有文献指出。
二、ATE的识别条件及倾向性得分匹配法
Rosenbaum和Rubin提出在如下强可忽略假设下,ATE可以被识别。
假设1(强可忽略假设):
(1)给定X时,(Y(1),Y(0))与Z条件独立;
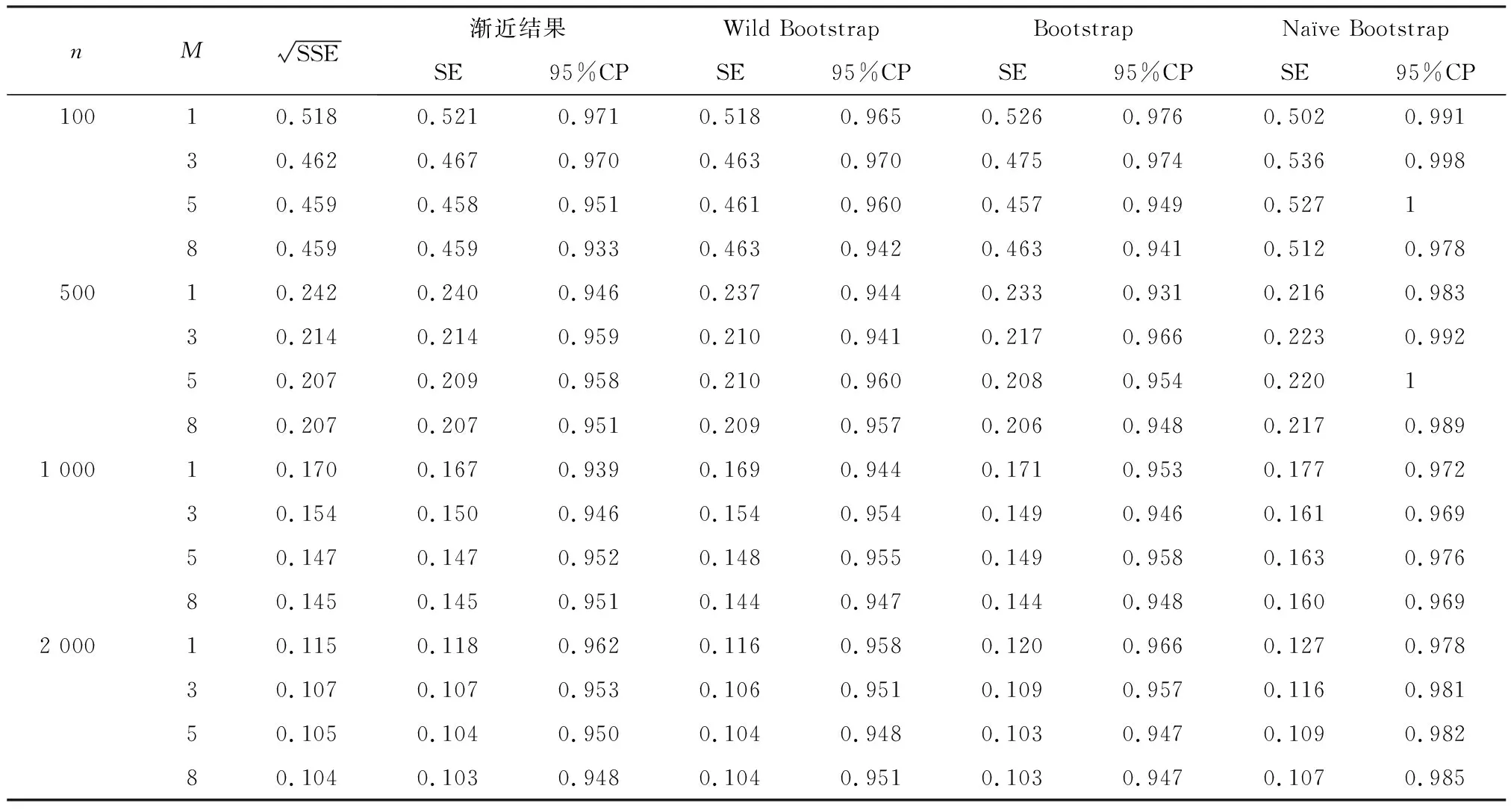
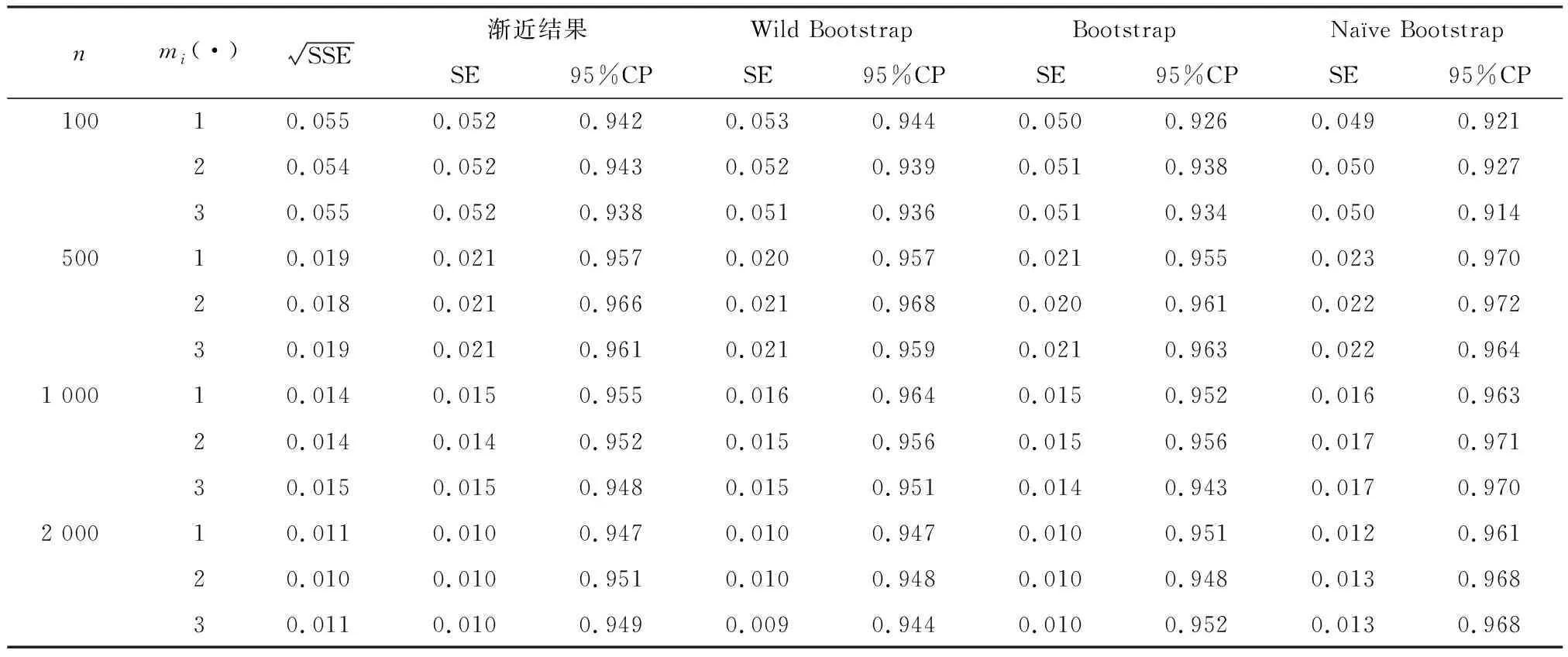
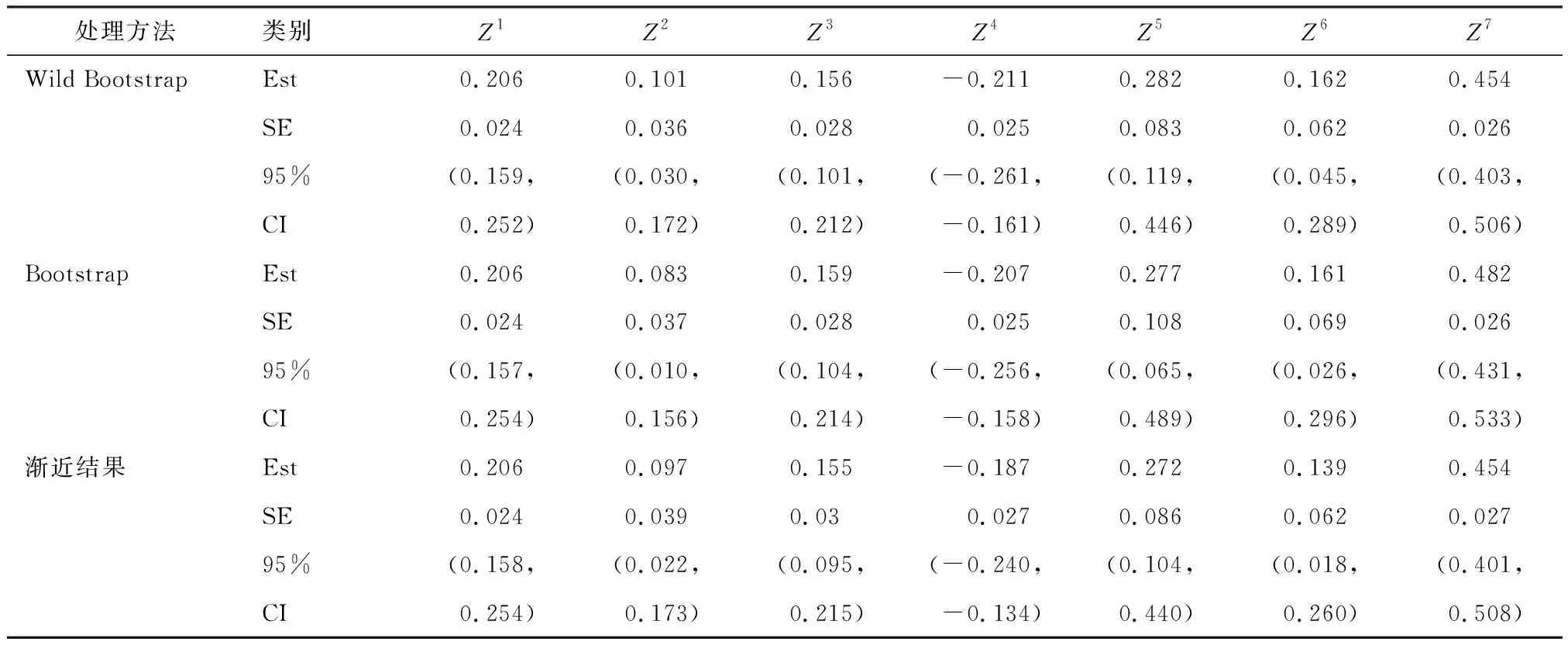
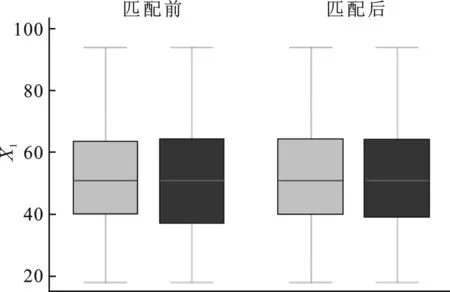
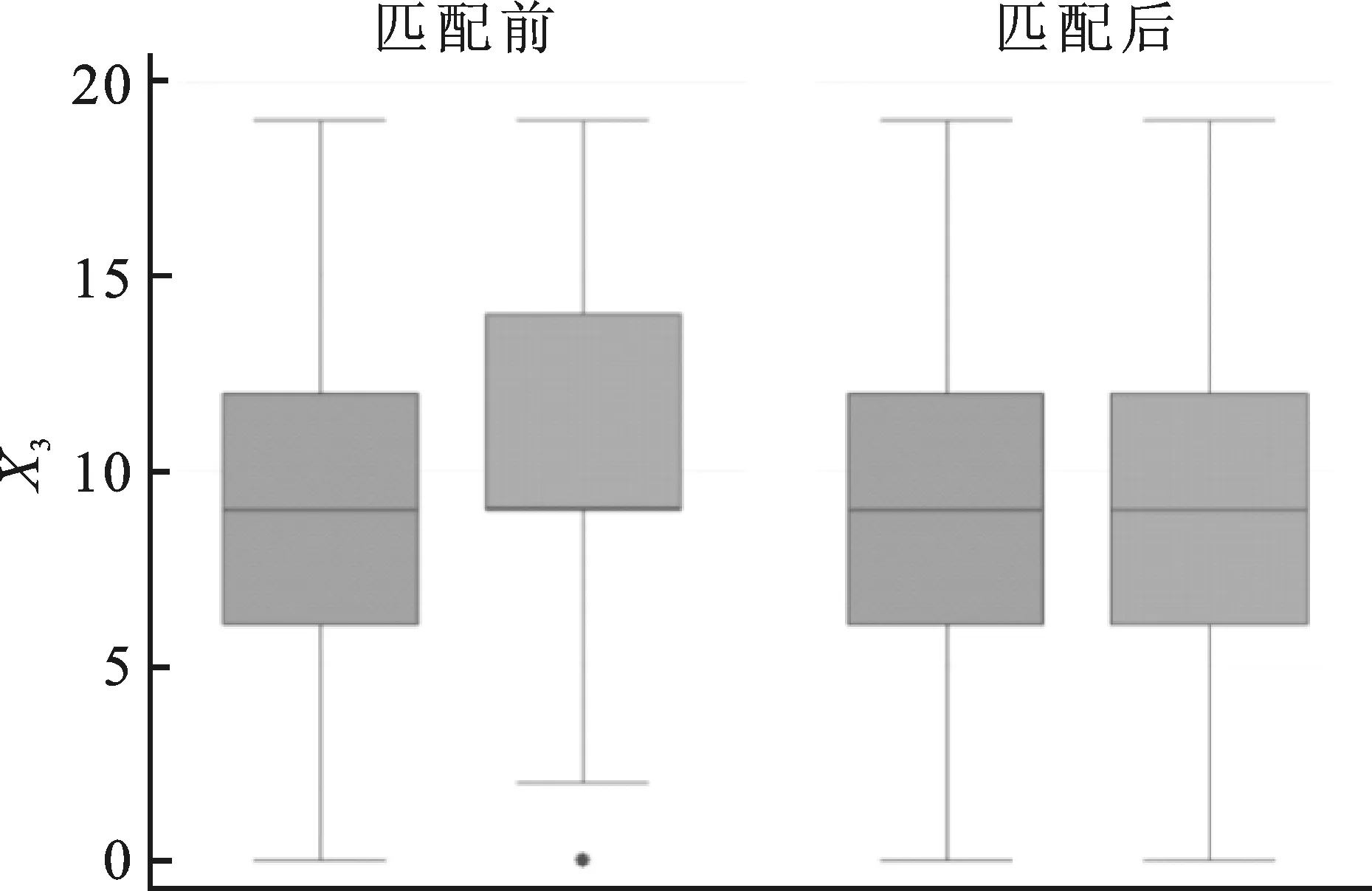
(2)倾向性得分p(X)=Pr(Z=1|X)满足0 τ=E[E(Y|Z=1,X)-E(Y|Z=0,X)] ATE的估计关键在于利用观测样本估计反事实结果,其中Yi(0)的M-最近邻匹配法估计可分别表示为: 及 其中,M表示固定的匹配个数,JM(i)表示个体i的匹配的指标集,其定义为: JM(i)= I[|p(Xi)-p(Xk)|≤|p(Xi)-p(Xj)|]≤M} 则ATE的M-最近邻匹配法估计为: 其中 表示第i个个体被匹配的次数。 (1) 则根据Härdle和Mammen,可以采用wild bootstrap。因此,加权自助法的研究思路是从wild bootstrap出发,对其权重进行一般化进而得到一般的加权自助法。 (2) (3) 其中 假设2: (2)对i=1,2,…,n有 假设2涵盖了几种常见的加权自助法,如非参数自助法,贝叶斯自助法以及wild bootstrap等,因此本文方法具有一定普适性[12-13]。 假设3: (2)E[Y|Z,p(X)]关于θLipschitz连续,其中θ为倾向性得分模型p(X,θ)中的参数。 下述定理1证明了在倾向性得分匹配场合,“OR”法的加权自助估计的分布弱收敛于倾向性得分配法的估计的分布,因此式(3)可用于固定匹配数时倾向性得分匹配法下ATE的统计推断。 定理1(1)篇幅限制,定理证明过程从略。有兴趣读者请来函向作者索取。:在假设1、假设2及假设3下,对∀r∈R有: 因此,若记: 诸如此类的情况,让这些殡仪馆工作的青年人,在专业得到工作单位认同和重视的情况下,感受到来自社会的职业声誉压力。 以下模拟是为了展示两种方法在有限样本下的表现,并设置了两种模拟情境:首先是在固定数据生成机制下结果随着样本量n和匹配数M变化的情况;其次是在固定匹配数M时,不同数据生成机制下结果随着样本量的变化情况。 第一种模拟情境的数据产生机制如下,协变量X1,X2独立同分布于U(0,1),残差e~N(0,1),响应变量为: 第二种模拟情境的数据产生机制效仿了“OR”方法,即: ξi~U(0,1),ζi~N(0,I3),εi~N(0,0.22) Xi=(X1i,X2i,X3i)′ Xji=ξi|ζji|/‖ζi‖,j=1,2,3 p(Xi)=0.15+0.7‖Xi‖ Zi=I(p(Xi)≥vi),vi~U(0,1) 响应变量为: Y=m(‖X‖)+2Z+e,e~N(0,0.22) 其中m(·)分别取为: m1(x)=0.15+0.7x m2(x)=0.1+x/2+exp(-200(x-0.7)2)/2 m3(x)=0.4+0.25sin(8x-5)+ 0.4exp(-16(4x-2.5)2) M-近邻取值M=5,bootstrap次数为500,样本量n分别取100,500,1 000,2 000。渐近结果,wild bootstrap,naive bootstrap与bootstrap的计算与第一种模拟情境的计算方式相同。 两种模拟情景的结果依次见表1和表2,其中“SSE”,“SE”和“95%CP”分别表示1 000次蒙特卡罗模拟下ATE匹配法mi(·)估计值的样本标准差,ATE标准差估计值的平均值和95%置信区间覆盖率。 表1 1 000次蒙特卡洛模拟结果 表2 1 000次蒙特卡洛模拟结果 本部分分别采用第三部分提出的两种自助法以分析性别、婚姻状况、健康状况、抑郁状况、劳动合同状况、是否党员和地区这7个因素分别作为处理变量时对收入的平均处理效应的估计。 本部分数据来自2016年中国综合社会调查数据(简称为CGSS),调查覆盖了全国28个省/市/自治区的478村庄,调查内容涉及受访者的性别、年龄、工作年限、教育程度、婚姻状况、健康状况和2015年全年收入等信息。本部分把2015年全年收入作为感兴趣的结果变量,并记为Y;感兴趣的处理变量分别为性别、婚姻状况、健康状况、抑郁状况、劳动合同状况、是否党员与地区,并依次记为Zj,j=1,2,…,7;年龄,工作年限和教育年限视为协变量并分别记为Xi,i=1,2,3。下面将分别研究处理变量Zj对收入影响的处理效应。 接下来将北京市、天津市、河北省、山东省、江苏省、上海市、浙江省、福建省、广东省、海南省视为东部地区,其余省份为非东部地区。删去了收入为0的样本,并将原始收入数据除以1 000后再对其取自然对数。经过处理后样本量为8 693,具体变量说明见表3。 表3 变量说明 表4 三种方法的ATE估计 图1 处理变量Z1匹配后协变量X1的平衡性检测① ① 其中匹配前、后的左侧均是对照组的箱线图,右侧均为处理组的箱线图。下同。 图2 处理变量Z1匹配后协变量X2的平衡性检测 图3 处理变量Z1匹配后协变量X3的平衡性检测 根据箱型图和密度函数图像在匹配前后的对比,协变量的平衡性有很大改变,特别是X2在匹配前后的变化尤为明显。图1说明协变量在根据Z1匹配后基本实现平衡,因此Z1的匹配法的结果具有一定可信度。其它处理变量的匹配后协变量的平衡性检测结果由于图像数量过多而在此处略去,仅通过展示处理变量Z1的平衡性检测结果以说明该检测的必要性。 根据表4,男性,已婚,身体健康,签有劳动合同,是党员以及东部地区对收入有正的影响效应,而抑郁对收入有负影响效应。具体而言,例如,男性的四种方法的ATE估计均是0.206,即男性年收入比女性将平均高出6 763.53元(不对原样本中收入做对数处理的结果);健康状况的ATE的bootstrap估计是0.159,即身体健康者的年收入比不健康者平均高出8 164.46元(计算方式同上男性情形);而抑郁的ATE的wild bootstrap估计是-0.211,即抑郁者的年收入比非抑郁者平均低3 586.43元。 通过模拟表明,两种方法与SSE及倾向性得分配法的渐近结果很接近并且在几种模拟情景中表现稳定,而对观测样本直接采用经典自助法(naive bootstrap)则通常差强人意。实证部分得出了几个常见社会因素如性别、婚姻状况、健康状态等对收入的影响效应,所得结果虽不能全面解释影响收入的原因,但为分析某单一因素对收入的影响提供了方法。 重点介绍了ATE的自助法推断,同样可将其推广至ATT(Average treatment effects for the treated)的方差及置信区间的推断。关于ATT的倾向性得分匹配法估计的大样本结论及协变量欧氏距离匹配法的加权自助法可分别参考Abadie和Imbens[5]及Otsu和Rai。
(一)ATE的匹配法估计
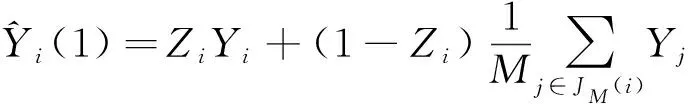
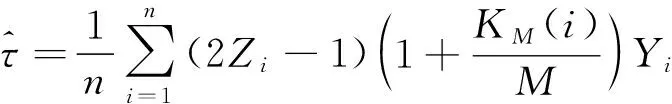
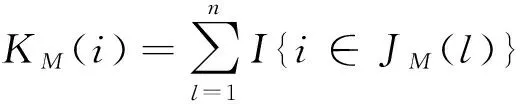
(二)倾向性得分
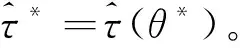
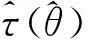
三、基于倾向性得分匹配法的ATE的自助法推断
(一)加权自助法


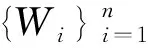
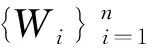

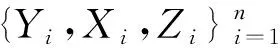
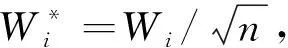
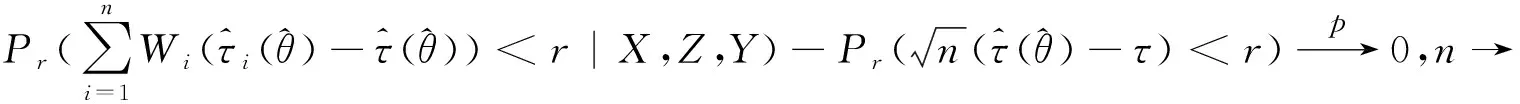
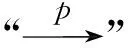
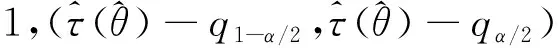
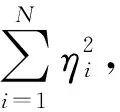
(二)经典自助法

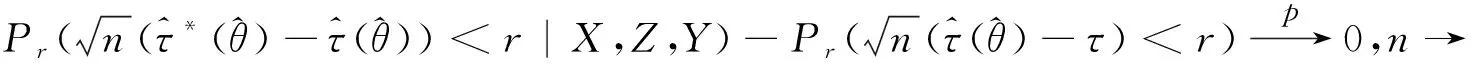
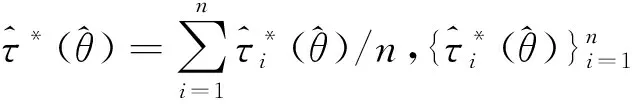
四、数值模拟
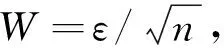
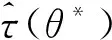
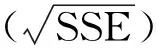
五、居民人均年收入的实证研究
(一)数据来源与描述

(二)分析与结果

六、结论与展望