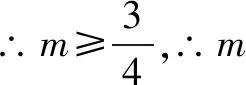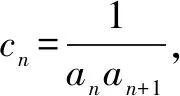例谈数列求和
——裂项相消法
2019-09-19赵秋鸣
赵秋鸣
(河北省唐山市第二中学 063000)
数列是高中数学的重要内容,又是学习高等数学的基础.等差数列,等比数列的通项,数列求和等问题,每年都是考查的重点.数列求和的问题需要根据数列特点选择解决方法,必须掌握常用的数列求和方法,数列求和的常见方法有错位相减法、裂项相消法、分解转化法、倒序相加法,数列求和往往和其他知识综合在一起,综合性较强.下面通过例题来说明用裂项相消法求数列前n项和,希望能对同学们有所帮助.
例1已知等差数列{an}的前n项和是Sn,等差数列{bn}的各项均为正数,且a1=1,S5=25,S2=b2,S4=b4.
(1)求{an}和{bn}的通项公式;

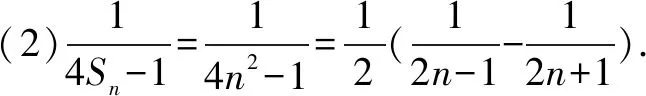

∴an=1+2(n-1)=2n-1.
∴S2=b2=4,S4=b4=16.
∵{bn}是各项均为正数的等比数列,

∴bn=b2qn-2=2n.

点评本题考查了等差数列与等比数列的通项公式与求和公式、裂项求和方法,考查了推理能力与计算能力.
例2已知数列{an}满足a1=1,an+1=2Sn+1,其中Sn为{an}的前n项和,n∈N*.
(1)求an;
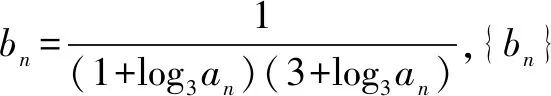
分析(1)数列{an}满足a1=1,an+1=2Sn+1,n≥2时,an=2Sn-1+1,相减可得:an+1-an=2an,即an+1=3an,利用等比数列的通项公式即可得出.
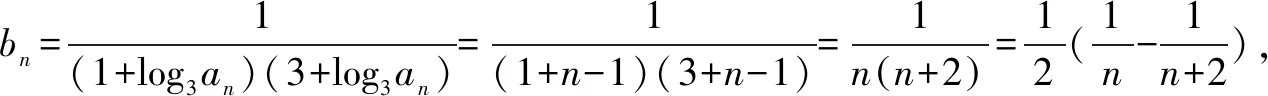
解(1)数列{an}满足a1=1,a2=2S1+1=3.an+1=2Sn+1,
n≥2时,an=2Sn-1+1,
相减可得:an+1-an=2an,即an+1=3an,n∈N*.
∴数列{an}是等比数列,公比为3,首项为1.
∴an=3n-1.
(2)数列{bn}满足
∴{bn}的前n项和为
对任意的正整数n都有Tn 点评本题考查了数列递推关系、等比数列的定义通项公式、裂项求和、数列的单调性、对数运算性质,考查了推理能力与计算能力. 例3设数列{an}的前n项和Sn,Sn=n2(n∈N*). (1)记bn=22n-1,求数列{bn}的前n项的和Tn; 分析(1)根据当n≥2时,an=Sn-Sn-1,当n=1时,a1=S1,求出an=2n-1,从而求出bn=22n-1,用等比数列的前n项和公式可得答案; (2)利用“裂项求和”即可得出. 解(1)当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1, 当n=1时,S1=1,∴a1=1,符合上式,∴an=2n-1. ∵bn=22n-1, 点评本题考查了等差数列前n项和与an的关系、等比数列的前n项和公式,裂项求和,考查了推理能力与计算能力. 分析因为Tn←bn←Sn←an←a1,d,所以应确定{an}的首项及公差. Tn=b1+b2+b3+…+bn 点评本题中的条件较多,通过分析找出基本量,简化条件,同时明确解题方向. 求数列{bn}的前n项和Tn使用的是裂项法. 通过以上例题的分析,我们可以看到由于条件不同,裂项方法不同,具有很强的灵活性,但我想信只要同学们在平时学习中多练习这类题,能够积累一些方法技巧,体会解法思路,肯定会有大的收获.