用对立统一观点判断二元一次不等式(组)表示的平面区域

陈玉田

(福建省仙游县盖尾中学 351200)

通常，在判断二元一次不等式Ax+By+C>0(或<0)所表示的平面区域时，要先确定直线Ax+By+C=0对平面区域的划分情况，再取特殊点计算其所在区域，从而确定不等式所表示的区域.根据坐标轴本身所具备的正负这一个对立统一性，这里介绍一种直接通过不等式系数A(或B)的符号来确定不等式所表示的区域.它不同于有些教参里用系数来记忆区域方向.

方法说明：A为x的系数，故应用来判断x轴的左右方向 (即水平方向)，将“>”、“<”视同“+”、“-”号(大于小于0嘛)，结合A的符号依“同号为正——区域在右，异号为负——区域在左”可以很容易判断，因为这与x轴的方向为左负右正恰好高度统一.

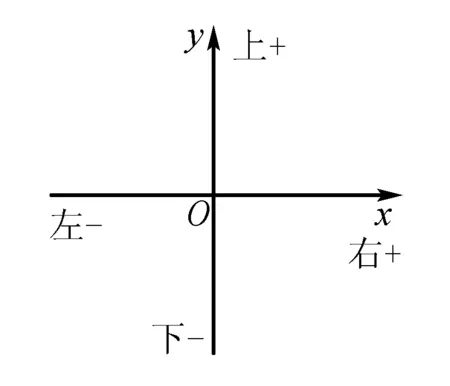
同理，B为y的系数，故应用来判断y轴的上下方向 (即竖直方向)，也将“>”、“<”视同“+”、“-”号，结合B的符号依“同号为正——区域在上，异号为负——区域在下”可以很容易判断，因为这与y轴的方向为下负上正也恰好统一.如上图.

举例说明，如判断不等式x-2y+3<0所表示的区域：将“<”视为负号，因为x的系数为正，则由异号为负，故知区域应在直线x-2y+3=0左侧，又因为y的系数为负，由同号为正，知其在直线x-2y+3=0上方，故知原不等式在直线x-2y+3=0的左上方.

这里对判断方法不作具体证明，只用极限值作简单验证.在平面上任取点P(x0，y0)，若令x0→+∞，y0=0，则易知点P(x0，y0)必在直线Ax+By+C=0右侧，又当A>0时，Ax0+By0+C>0，从而根据特殊点定域法知：A>0时，不等式Ax+By+C>0表示的区域在直线Ax+By+C=0右侧；不等式Ax+By+C<0表示的区域在直线Ax+By+C=0左侧.A<0依此类推.

同理，令x0=0，y0→+∞同样可判断：B>0时，不等式Ax+By+C>0表示的区域在直线Ax+By+C=0上方；不等式Ax+By+C<0表示的区域在直线Ax+By+C=0下方.B<0依此类推.

此法很好地把x、y两条不同的坐标轴本身的正负特性统一了起来，故判断极为简单，无需计算，也无需记忆.

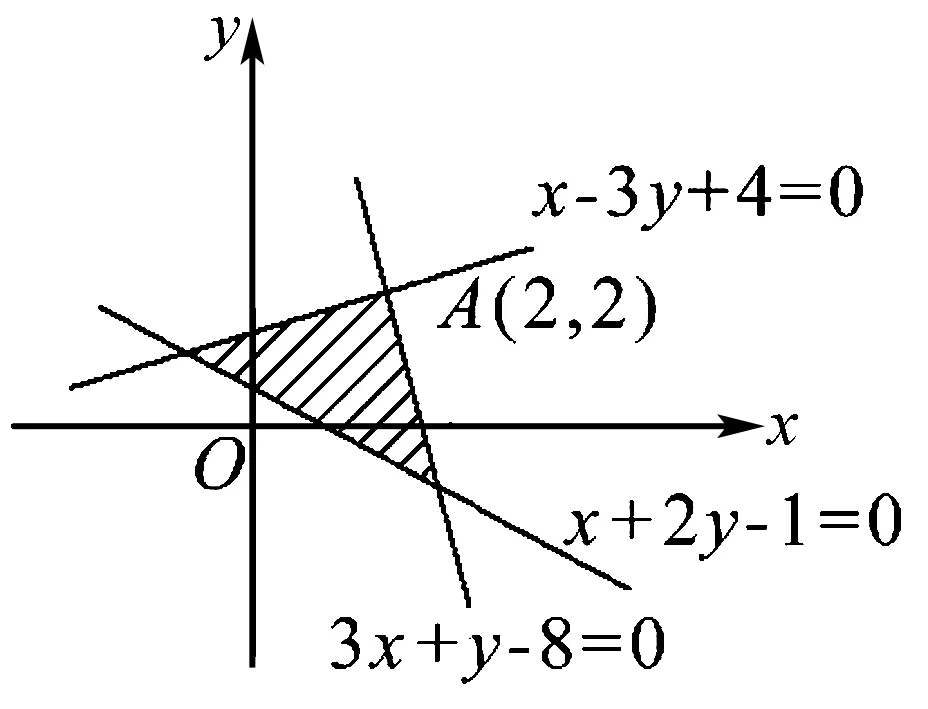
分析不等式x-3y+4≥0中，视“≥”为正，因为x的系数为正，同号取右；y的系数为负，异号取下，故区域在直线x-3y+4=0的右下方；同理区域在直线x+2y-1=0的右上方，在直线3x+y-8=0的左下方，即知不等式组表示的区域如右图所示.

最后顺便一提，实际操作时，只需取x的系数作左右判断(或取y的系数作上下判断)，二选一即可.