对叠加问题中一道定值模型解法探讨

陈 明

(江西省玉山县第一中学 334700)

一、引言

叠加问题是高中运动学中学常见类型，知识综合性大，难度大，特别是物体间的相对运动，很多同学难以理解.本文将结合一道定值问题，对这类问题的求解方法进行探讨.

二、例题解析

例长为L、质量为M的平板小车停在光滑水平面上，质量为m的木块(可视为质点)以速度v0滑上小车的左端，最后停在小车的右端，如图1甲所示；若小车以速度v0向左运动时，将木块轻轻地放在小车左端，如图1乙所示，则( ).

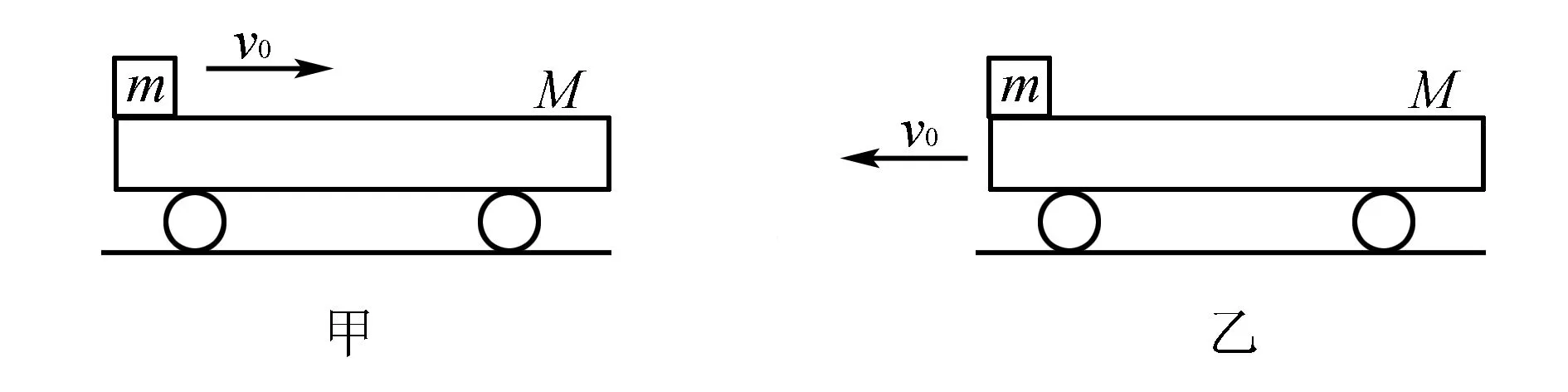
图1

A.木块最终刚好停在小车右端

B.木块最终停在小车上，但还离右端一段距离

C.木块将滑出小车

D.两种情况中木块相对小车滑行的时间相等

解法一根据运动学知识求解.

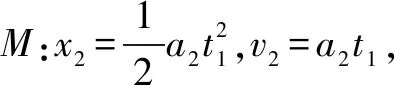
木块最终停在小车右端，所以v2=v1

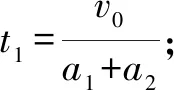
对乙，木块和小车受力情况与甲相似，因此在运动过程中木块和小车加速度的大小与图甲对应的加速度大小相等.假设木块最终停在小车上，则木块与小车最终的速度大小相等，

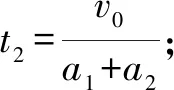
因此有t1=t2，△L=L，故假设成立，木块恰好停在小车的右端.

解法二根据动量知识求解.

对甲，根据动量守恒定律有mv0=(M+m)v1，

根据能量守恒有

对乙，根据动量守恒定律有Mv0=(M+m)v2，

根据能量守恒有

因此有△x=L，t1=t2.

解法三转换参考系.

对甲，木块：a1=f/m，方向向左，

小车：a2=f/M，方向向右，

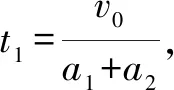
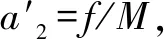
解法四利用v-t图像求解.

根据木块和小车运动关系，甲中木块和小车的v-t图像如图2所示，乙中木块和小车的v-t图像如图3所示，对于图甲、图乙，木块和小车受力情况相似，因此甲中木块和小车在运动过程中的加速度的大小与乙中对应的加速度大小相等，对应v-t图像中的直线斜率大小相等，从而可得两种情况下木块相对小车滑行的时间相等.

甲、乙v-t图象中的两直线所围三角形为木块与小车之间的相对距离，即木块在小车上滑行的距离，因为两v-t图象中时间相等，所以两v-t图象中三角形所围面积相等，即两种情况下木块在小车上滑行的距离相等.

因此两种情况下木块在小车上滑行的距离相等，木块在小车上滑行的时间相等.

通过以上几个方法分析，不难得出：

1.两种情况下木块在小车上滑行的距离相等，木块在小车上滑行的时间相等.这种模型是定值模型.

2.在解题过程中，可以从不同角度来分析问题，拓宽思路提升能力.

3.在这几种求解方法中，都设定了未知量，利用未知量但并没有求解未知量，这是一种较好的解题思路：“设而不求”，巧设未知量以求解问题.