小学生几何直观能力的培养

毛凯捷

摘要：小学数学以简单的几何和计算为主，其中几何知识较为浅显，是学生后续深入学习平面几何与立体几何的基础。新课标中明确要求，培养学生的几何直观能力。本文以小学数学教学中如何培养小學生的几何直观能力为对象，并提出部分科学举措。

关键词：小学数学;几何直观能力;培能

几何通常被喻为“心智的磨刀石”，几何直观能力即为通过对几何图形的分析与描述，将复杂的数学问题变得清晰化和简单化，帮助小学生找出探究问题和解决问题的最佳思路，将学习变得轻松愉悦。在小学数学课程教学中，教师应积极响应新课标的理念与要求，着重培养学生的几何直观能力，引领学生利用图形描述和分析数学问题，掌握高效的学习方法，且数学思维能力得以有效锻炼。

识图画图培养几何直观能力

图形和几何属于小学数学教学的关键构成部分，帮助学生掌握有关图形的基础知识，能够为他们下一步系统的学习几何知识奠定良好基础。在小学数学日常教学中，教师应从最基本的识图和画图切入，使学生在识图过程中知道图形的名称、了解特征和感受概念，再利用画图深化对图形的理解与认知，让学生体会几何直观能力的价值与作用。

例如，在进行“三角形”教学时，教师可先设计问题：生活中哪些物体上有三角形？像三角架、小红旗、路标、三明治和三角锥等，利用生活实例帮助学生认识三角形，学生通过对三角形的观察，得出三角形的特点：有3条边，3个角;3条边都是线段;这3条线段要首尾相接地围起来。并指导只有3条线段首尾相接围成的图形才是三角形。接着，教师要求学生自主尝试画一个三角形，把生活中的实例通过画图的形式展现出来，在展示环节，可以发现同学之间画出的三角形形状不同，有的角大，有的角小，利用画图和观察引导学生发现：不在同一条直线上的3个点都能画出一个三角形。

如此，学生通过对三角形图形的认识和亲自画图，在动手操作与观察比较中认识三角形的特点，理解和掌握三角形的定义，使他们初步体会到几何直观能力对学习数学知识的作用。

数形结合提升几何直观能力

我国著名数学家华罗庚曾说过“形缺数时难入微，数缺形时少直观。”数形结合思想作为一个重要的数学思想，能有效把数和形整合在一起，将抽象问题转变成具体问题的关键思考方法。数形结合思想能够把数学问题数量关系及运算等同几何图形结合起来，发挥“数”和“形”的优势互补作用。小学数学教师应用数学结合思想，引导学生将形象思维与逻辑思维有机统一，借此发展与提升学生的几何直观能力。

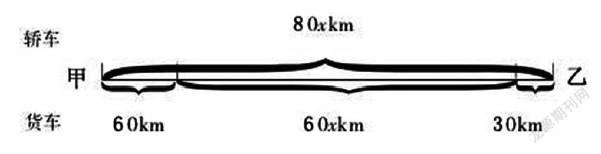
在学习“简易方程”过程中，针对部分较为复杂的难题，教师可组织学生采用画线段图的方式分析和解题，把有关数的问题转化成形的问题。如一辆轿车与一辆货车从甲地驶往乙地，货车先行驶1小时后轿车才出发，其中轿车的速度是80千米/小时，货车的速度是60千米/小时，最终是轿车比货车早到30分钟，那么甲乙两地相距多少千米？针对这一问题，教师可指导学生利用画线段图的方式分析题目中的数量关系，他们可以设：轿车用x小时到达乙地，线段图如下：

这样学生能够直观明了的表示题目中的数量关系，列出方程：80x=60+60x+30，解得x=4.5小时，故甲乙两地相距80×4.5=360千米。

上述案例中，教师引领学生将数形结合思想巧妙运用至解题中，有利于学生对数学知识的进一步认知，使其学会借助几何直观能力解答问题，借此培养学生的几何直观能力。

联系实际发展几何直观能力

大部分小学数学知识都源于生活，把现实生活中的问题通过图形来表示，能够将复杂的问题变得形象、简明，也可以结合图形判断结果，这就是几何直观能力的价值所在。为此，小学数学教师在讲授部分概念时，可适当引入一些实际生活中的素材，创设生活化课堂情境，引领学生借助几何直观能力学习数学知识，发展他们的几何直观能力。

在教学“轴对称”数学概念时，教师可先在多媒体课件中出示生活中的蝴蝶图片，提问：同学们，你们观察一下蝴蝶图，讨论蝴蝶的形状有什么特点？继续展示枫叶、蜻蜓、雪花的图片，让学生仔细观察这几种实物，思考它们有什么共同特征？总结：像这样两边形状、大小相同的物体，就说它是对称的。追问：像这样对称的物体，现实生活中还有哪些？他们将会想到酒瓶、扇子、风筝等。接着，教师要求学生将蝴蝶的形状画出来，得出一个平面图形，研究其是否对称？让他们想办法折一折，可以发现：沿着图形中的一条直线对折后折痕两边的图形完全重合，初步认识这条折痕就是图形的对称轴。在上述案例中，教师联系生活实际带领学生学习“轴对称”这一数学概念，深化他们对对称现象的理解与认知，提高学生的学习效率，并锻炼学生的几何直观能力。

在小学数学教学实践中，教师应当根据具体教学内容恰当设计几何直观教学，指导学生采用正确的学习方法与思考方式，着重培养学生的几何直观能力，借此提高学生的数学知识水平与学习能力，为后续深入学习打下扎实根基。

（作者单位：江苏省启东市龚家镇小学）